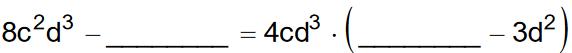Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Berechne den Wert des Terms. (1 BE)
- 2
Simon wird ein Gedicht vorgelegt. Beschreibe, wie er die relative Häufigkeit ermitteln kann, mit der der Buchstabe „e" in diesem Gedicht vorkommt. (1 BE)
- 3
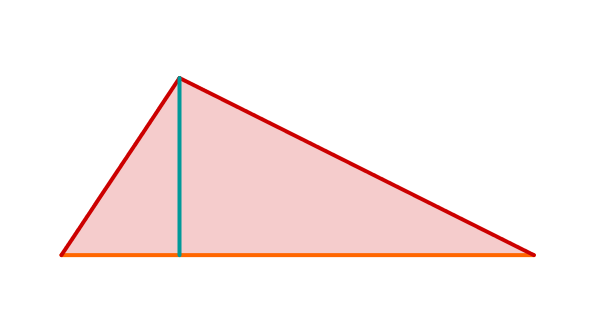
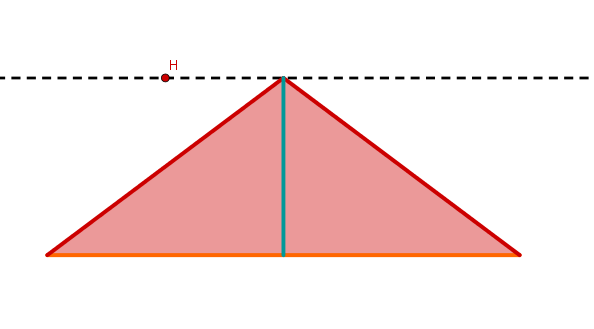
Jakob behauptet „Alle Dreiecke, die in der Länge einer Seite und der Länge der zugehörigen Höhe übereinstimmen, sind kongruent."
Begründe durch zeichnerische Darstellung eines Gegenbeispiels, dass Jakobs Aussage falsch ist. (1 BE)
- 4
Ein Schwimmbecken ist 2 m tief, 50 m lang und 14 m breit. Im Schwimmbecken befinden sich 100 Personen. Pro Person werden durchschnittlich 70 Liter Wasser verdrängt. Berechne, um wie viele Zentimeter der Wasserspiegel sinkt, wenn alle Personen das Becken verlassen und kein Wasser nachgefüllt wird. (2 BE)
- 5
Hannah klammert korrekt aus. Ergänze ihre Rechnung sinnvoll. (2 BE)
- 6
Ein Quadrat mit der Seitenlänge x cm wird mit einem Rechteck verglichen, dessen Länge um größer und dessen Breite um kleiner ist als die Seitenlänge des Quadrats. Berechne den Wert von x, für den der Flächeninhalt des Rechtecks um kleiner ist als der des Quadrats. (2 BE)
- 7
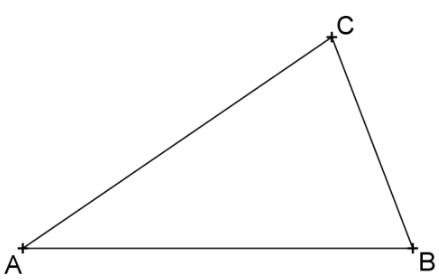
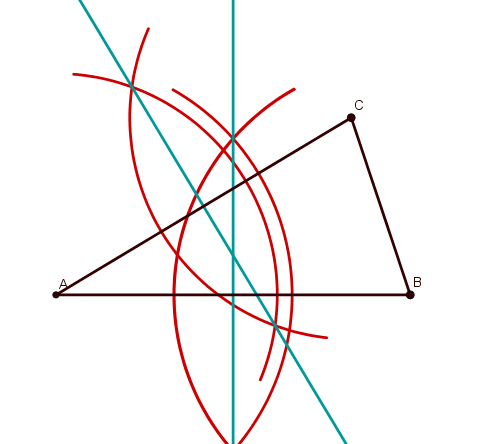
Die Abbildung zeigt das Dreieck .
Konstruiere im abgebildeten Dreieck die Mittelsenkrechte der Seite und die Mittelsenkrechte der Seite . (1 BE)
Der Schnittpunkt der Mittelsenkrechten der Seite und der Mittelsenkrechten wird mit bezeichnet. Charlotte erklärt einer Mitschülerin, dass der Umkreismittelpunkt des Dreiecks ist. Ergänze sinnvoll, was sie ihrer Mitschülerin gesagt haben könnte. (2 BE)
- 8
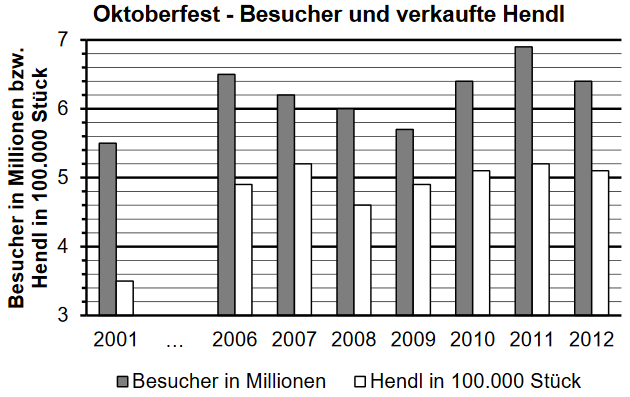
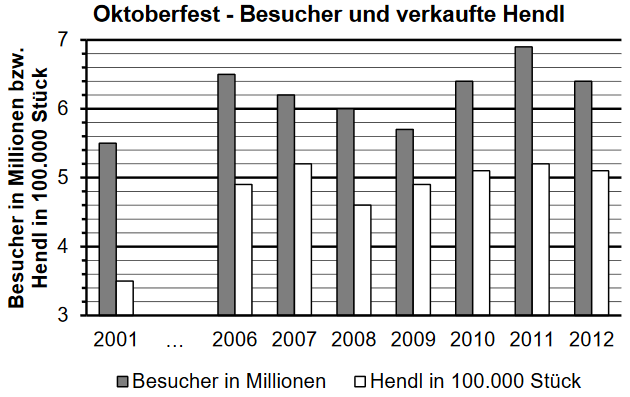
Das Oktoberfest ist ein jährlich in München stattfindendes Volksfest. Die Abbildung zeigt für verschiedene Jahre die Anzahl der Besucher des Oktoberfests und die Anzahl der dort verkauften Hendl.
Gib an, wie viele Personen das Oktoberfest im Jahr 2012 besuchten. (1 BE)
Kreuze (nur) diejenigen Aussagen an, die mit dem Diagramm in Einklang stehen. (2 BE)
Im Jahr 2013 kamen aller Besucher aus Bayern, der Besucher aus Bayern lebten in München. Berechne für das Jahr 2013, wie viel Prozent aller Besucher in München lebten. (1 BE)
Um die Anzahl aller Besucher näherungsweise zu ermitteln, werden auch Luftbildaufnahmen verwendet. Die Anzahl der Personen auf der abgebildeten Aufnahme kann man abschätzen, ohne alle Personen zu zählen. Beschreibe, wie man dazu vorgehen könnte. (2 BE)
- 9
Marie wirft dreimal einen Spielwürfel mit den Augenzahlen 1 bis 6. In der Reihenfolge der Würfe notiert sie nacheinander die drei erzielten Augenzahlen als Hunderter-, Zehner- bzw. Einerziffer einer dreistelligen Zahl.
Berechne, wie viele Möglichkeiten es für die dreistellige Zahl gibt. (1 BE)
Bestimme, wie viele Möglichkeiten es für die dreistellige Zahl gibt, wenn diese mindestens zweimal die Ziffer 6 enthält. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?