Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
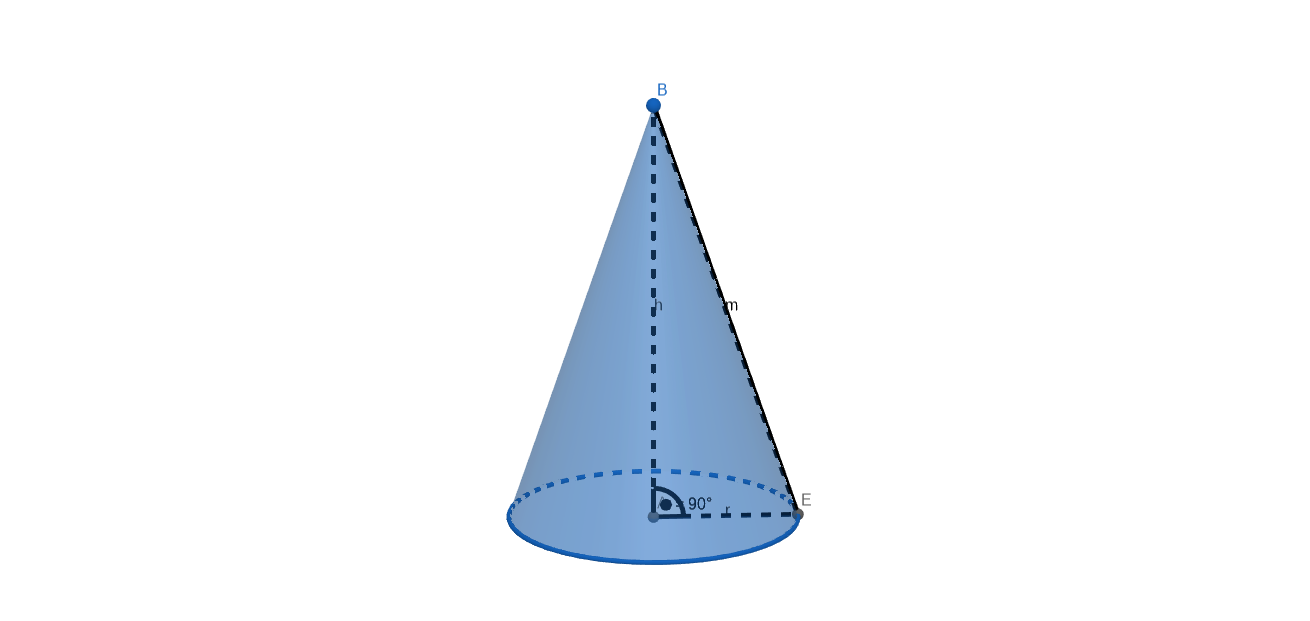
Ein gerader Kreiskegel hat den Radius r, die Höhe h und die Mantellinie m. Die Skizze zeigt den Kegel und ein zugehörigesStützdreieck.
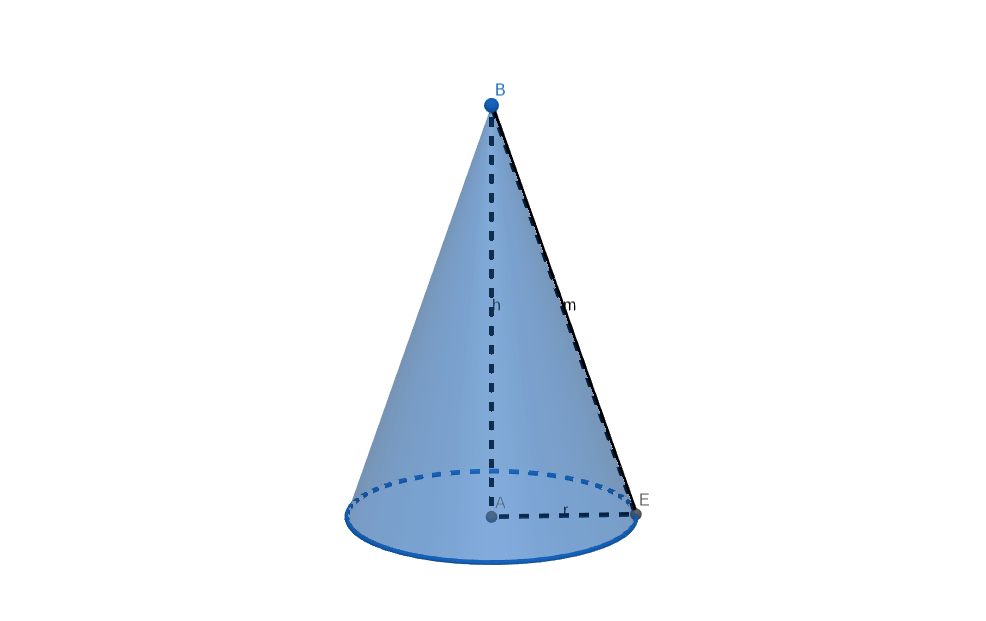
Kreuze (nur) die richtigen Gleichungen an. (1 BE)
Für den Inhalt der Oberfläche des Kegels gilt die Formel .
Gib für die beiden Summanden der Formel, und , jeweils die Bedeutung für den Kegel an. (1 BE)
Löse die Formel nach auf. (1 BE)
Die Größen und werden jeweils verdreifacht.
Dann … sich der Inhalt der Oberfläche des Kegels. (1 BE)
- 2
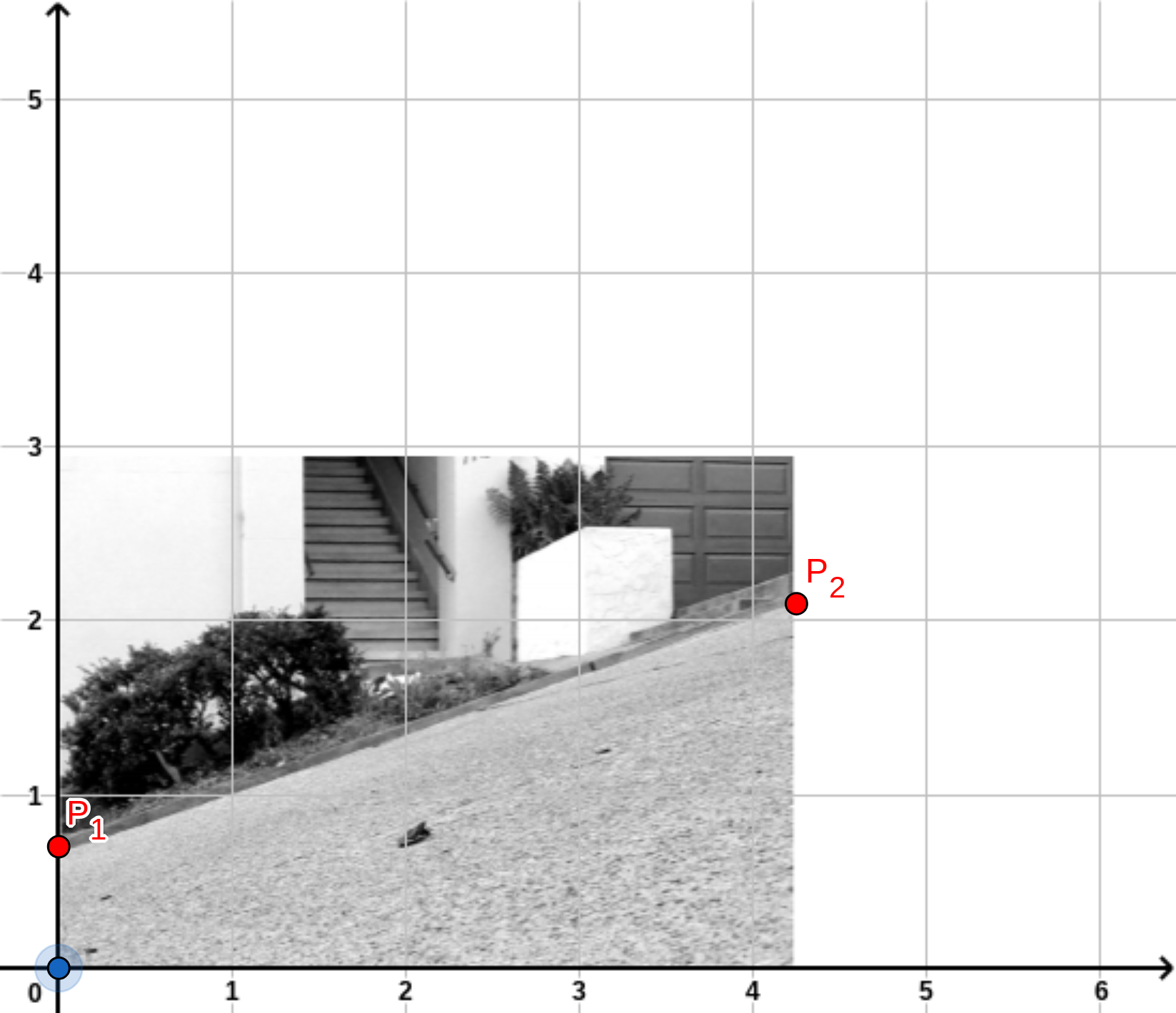
Eine der steilsten Straßen der Welt ist die Filbert Streetin San Francisco. Bestimme mithilfe der Abbildungihre Steigung in Prozent. (2 BE)
Hinweis: Die Steigung einer Straße ist wie die Steigung einer Geraden im Koordinatensystem festgelegt.
- 3
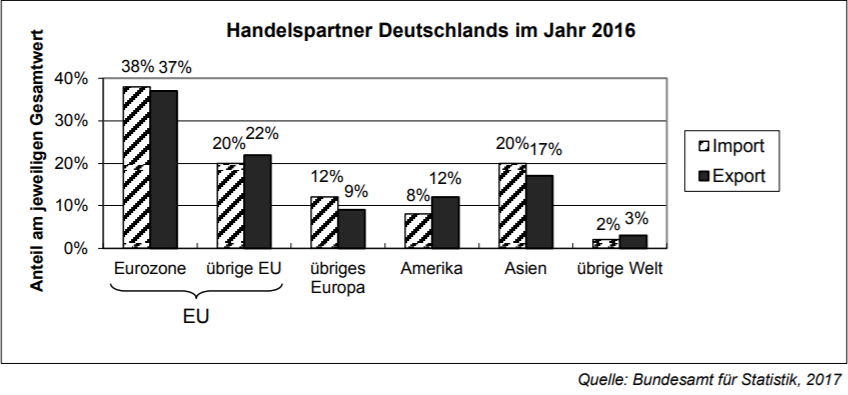
Im Jahr 2016 betrug der Gesamtwert der Importe Deutschlands 950 Mrd. €, der seiner Exporte1200 Mrd. €. Das Diagramm zeigt, wie sich diese Gesamtwerte auf Deutschlands Handelspartnerverteilten.
Berechne mithilfe der Daten des Diagramms, wie viel Prozent der Importe, dieDeutschland aus Europa bezog, auf die EU entfielen. (2 BE)
Gib an, warum 4% von 1200 Mrd. € nicht den Betrag ergeben, um den sich der Wert der Exporte nach Amerika vom Wert der Importe aus Amerika unterscheidet. (1 BE)
Deutschland hatte 2016 etwa 82 Millionen Einwohner. Wie groß ist in etwa der Wert derdeutschen Exporte, der auf einen Einwohner entfiel? (1 BE)
- 4
In Analogie zu einem Spielwürfel wird ein quaderförmiger Tafelschwamm geworfen.

Für das einmalige Werfen des Schwammes wurde experimentell folgendes Modell ermittelt:
Elementarereignis
"Eine der beiden größten Seitenflächen oben"
"Eine der beiden kleinsten Seitenflächen oben"
"Eine der beiden übrigen Seitenflächen oben"
Wahrscheinlichkeit
0,83
0,04
0,13
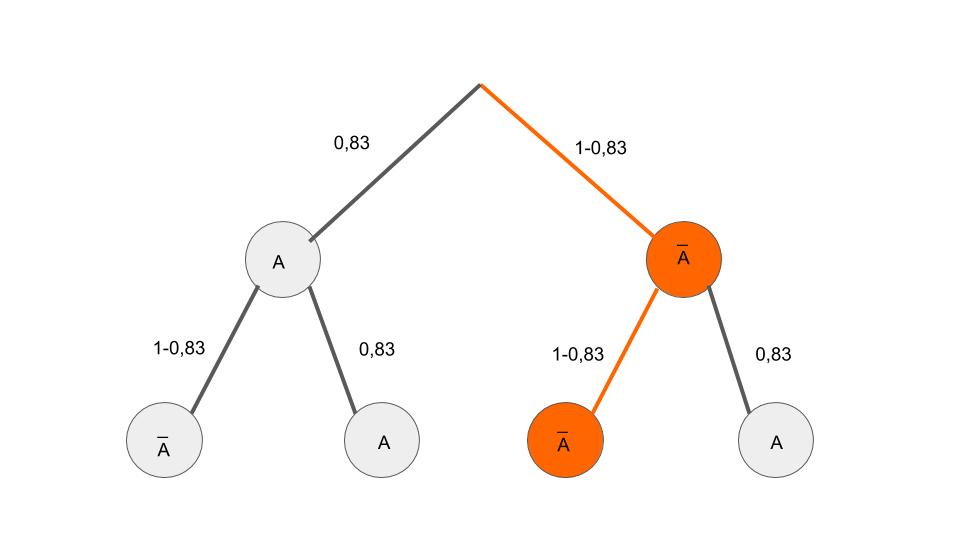
Beschreibe, wie man experimentell einen Schätzwert für die Wahrscheinlichkeit des Ereignisses „Der Tafelschwamm landet bei einmaligem Werfen so, dass eine der beiden kleinsten Seitenflächen oben liegt.” ermitteln kann. (1 BE)
Begründe anhand der Tabelle, dass dieses Zufallsexperiment kein Laplace-Experimentist. (1 BE)
Der abgebildete Schwamm wird einmal geworfen. Gib ein Ereignis an, dessenWahrscheinlichkeit 87% beträgt. (1 BE)
Der abgebildete Schwamm wird zweimal geworfen. Kreuz an, mit welcher Wahrscheinlichkeitder Schwamm dabei nie auf eine der beiden größten Seitenflächen fällt. (1 BE)
- 5
Gegeben ist die Parabel mit dem Funktionsterm p(x)=3x²-8x+7
(vgl. Abbildung)
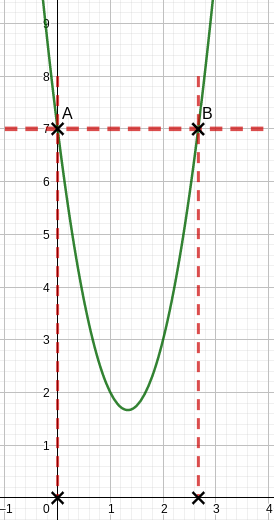
und sind die Lösungen der Gleichung p(x)=7 .
Bestimme graphisch Näherungswerte für und .Gib an, wie man aus und den x-Wert desParabelscheitels ermitteln kann. (2 BE)
Bestimme rechnerisch die Lösungen und der Gleichung p(x)=7. (2 BE)
- 6
Hannah erklärt Simon, wie man schrittweise die Quadratzahlen berechnen kann.„Wenn du zum Beispiel 8²=64 berechnet hast, geht die Berechnung der nächsten Quadratzahl ganz einfach. Du musst nur zur ‚alten‘ Quadratzahl 64 die ‚alte‘ Basis 8 und die‚neue‘ Basis 9 addieren, also 64 + 8 + 9 = 81, und das ist das Quadrat von 9.“
Wende Hannahs Regel auf ein weiteres Zahlenbeispiel an. (1 BE)
Begründe durch eine allgemeine Rechnung, dass Hannahs Regel für jede„alte“ Basis n (n ) gilt. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?