Aufgaben zu den Formeln für das Volumen von Prismen und Zylindern

1
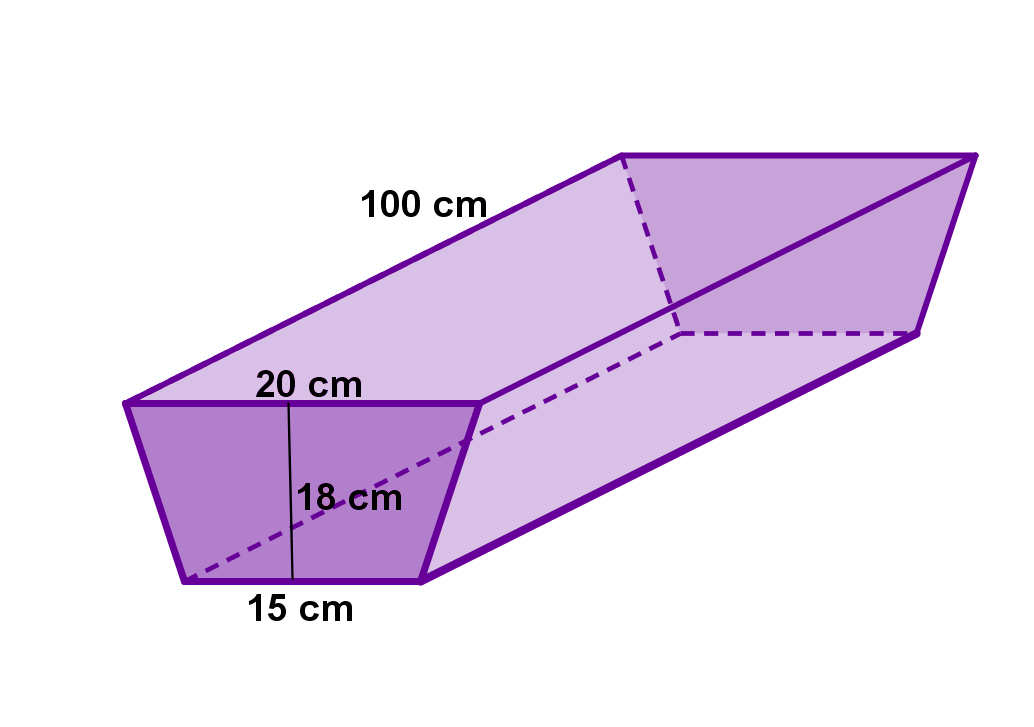
Filmon hat einen Blumenkasten. Der Blumenkasten hat 100 cm Länge und 18 cm Höhe. Unten ist er 15 cm breit und oben 20 cm. Wie groß ist das Volumen des Blumenkastens?
cm³
2
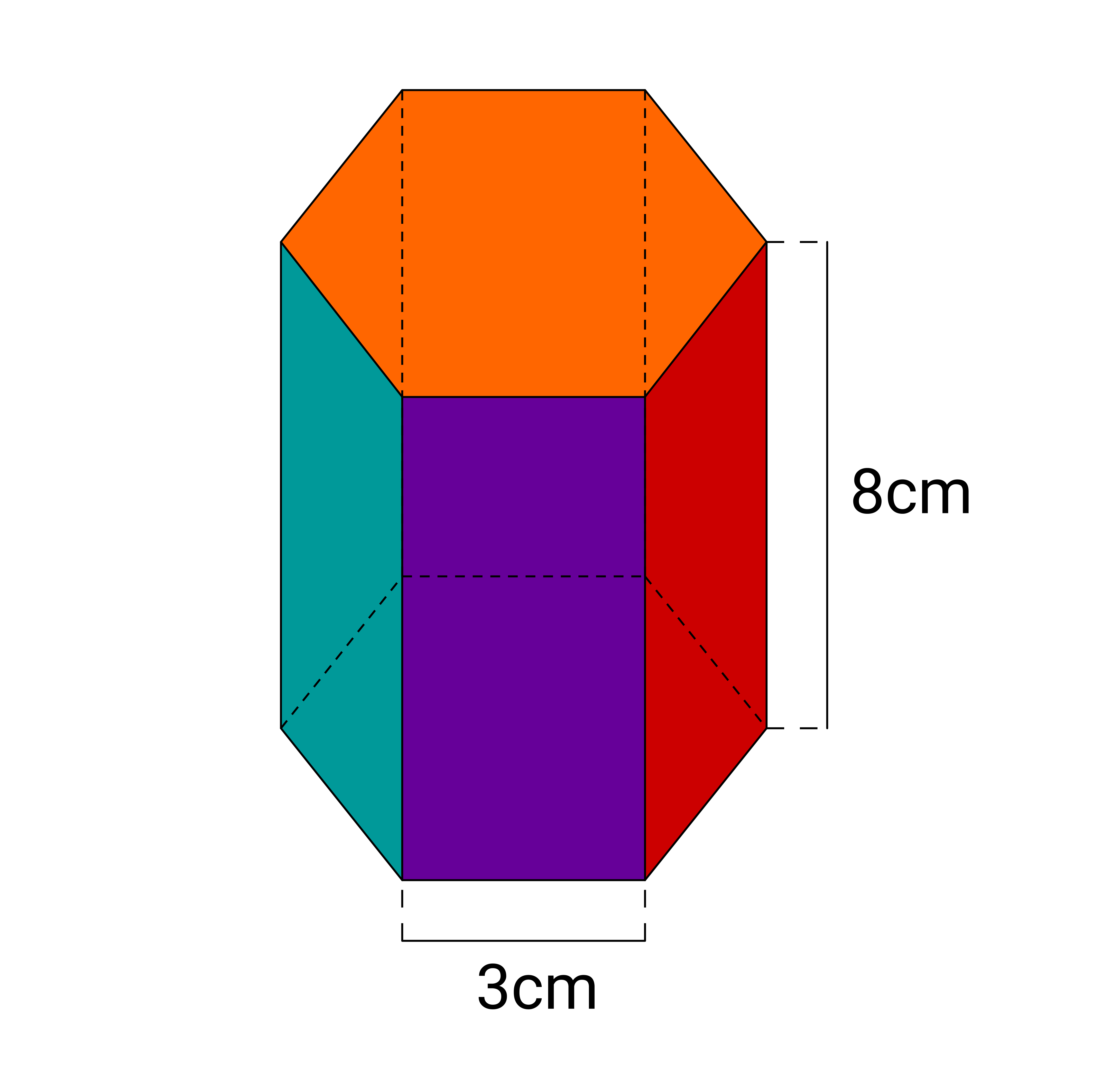
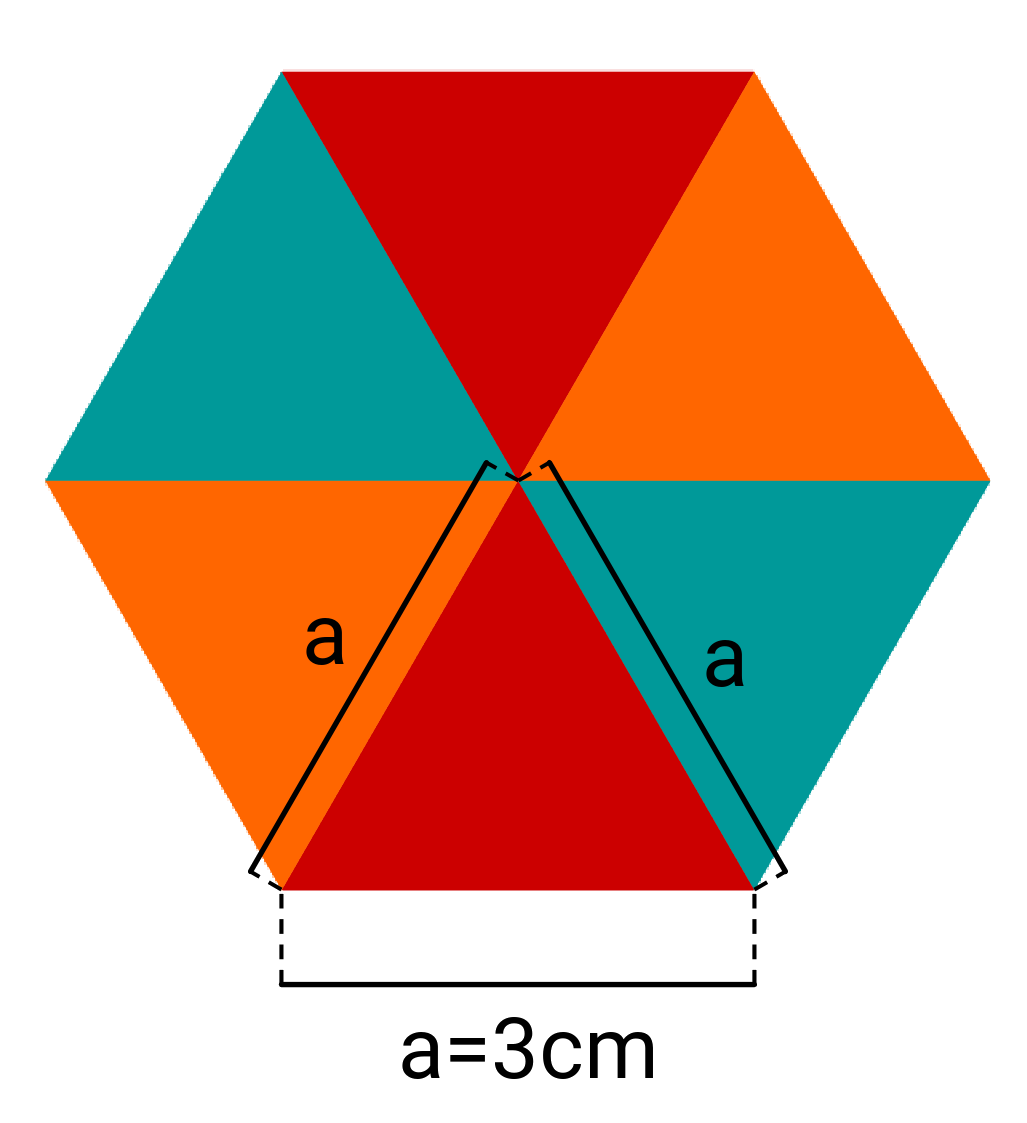
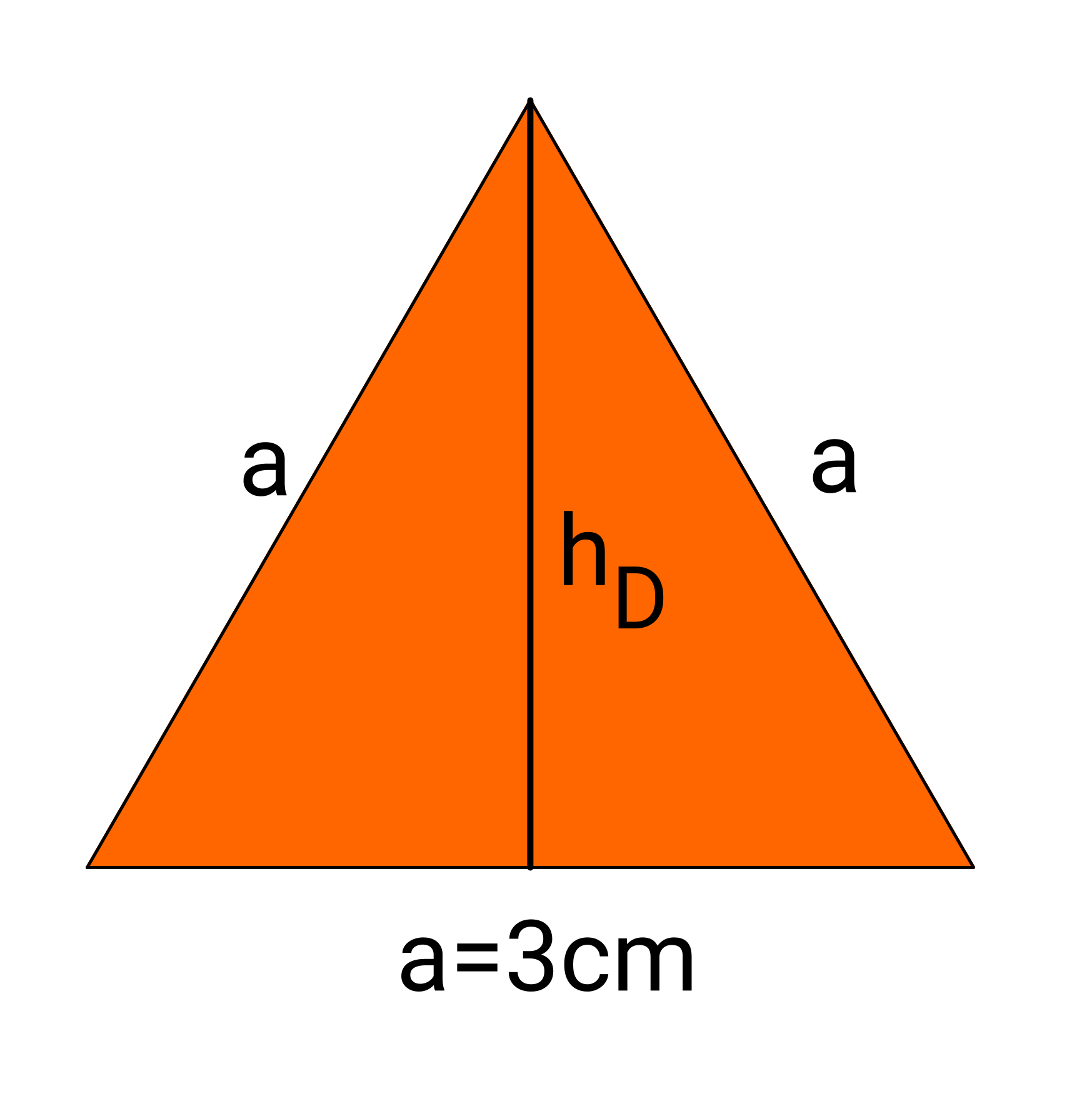
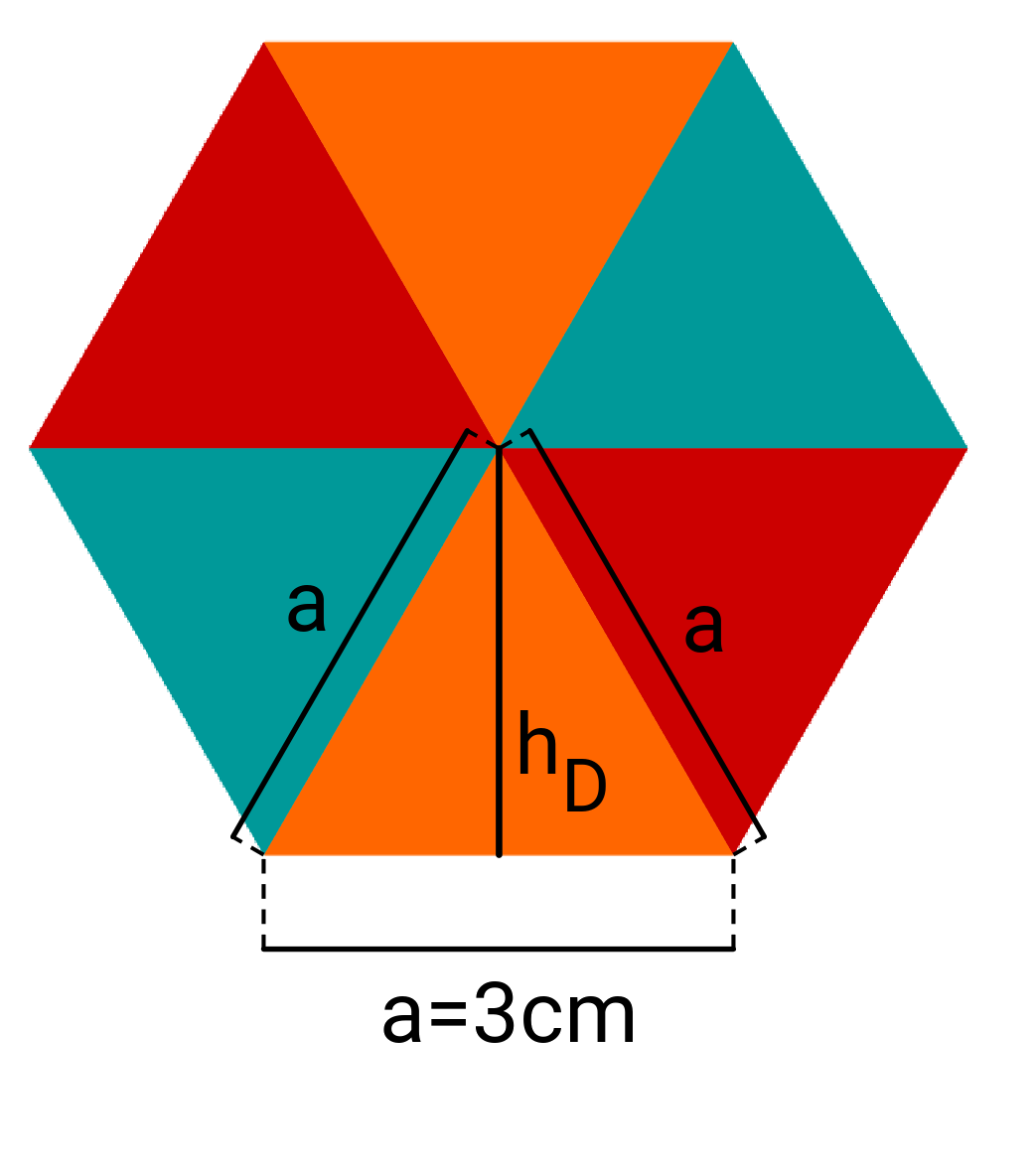
Ein Marmeladenglas hat als Grundfläche ein regelmäßiges Sechseck und ist (abgesehen vom Rand mit Schraubverschluss und Deckel) $8\;\text{cm}$ hoch. Die Seitenlänge des Sechseckes ist $3\;\text{cm}$ .
Wie viel Milliliter Marmelade passen in das Glas, wenn man es bis unter den Rand füllt?
ml
3
Der Durchmesser des Mülleimers ist 30 cm und die Höhe ist 60 cm (ohne den Deckel). Wie groß ist das Volumen?
Runde auf ganze $cm³$ .
cm³
4
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Ein zylindrisches Ausdehnungsgefäß hat d=35cm Durchmesser und h=450mm Höhe.
Wie viel Liter fasst das Gefäß?
5
Dieses Glas hat einen Durchmesser von 7 cm und seine Höhe ist 8 cm.
Berechne das Volumen des Glases. Runde dein Ergebnis auf Einer.
6
In ein Glas mit dem Innendurchmesser 8 cm werden 150 ml Wasser eingegossen.
Wie viele cm steht das Wasser im Glas? Runde auf ganze Zahlen.
7
Welches Volumen hat ein $4{,}5\, \mathrm{m}$ hohes Haus mit der Breite $4\, \mathrm{m}$ und der Länge $7\, \mathrm{m}$ , wenn das Dachgeschoss $2 \, \mathrm{m}$ hoch ist?
Quelle: torange.biz, CC-BY-SA-4.0
8
Gegeben ist ein Zylinder mit einer Oberfläche von $150{,}72cm^2$ und einem Durchmesser von $6cm$ .
Berechne die Höhe des Zylinders.
cm
9
Herr Müller möchte ein Kabel mit einem Volumen von $0{,}63 \,\mathrm{m^3}$ verlegen. Der Radius beträgt $10 \,\mathrm{cm}$ . Berechne die Länge des Kabels. Runde beim Ergebnis auf ganze Zahlen.
m
10
Eine Getränkedose hat eine Höhe $h$ von $16{,}8 \text{cm}$ . Der Durchmesser $d$ beträgt $6{,}7 \text{cm}$ . Berechne das Volumen der Dose.
Runde dein Ergebnis auf ganze Zahlen.
cm³
11
Ein zylinderförmiger Lautsprecher hat eine Höhe von $h = 18 \,\mathrm{cm}$ . Der Radius beträgt $r = 3{,}75 \,\mathrm{cm}$ . Berechne das Volumen.
Runde dein Ergebnis auf ganze Zahlen.
cm³

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?