Aufgaben zum Satz des Pythagoras
- 1
Gib für die rechtwinkligen Dreiecke jeweils die Gleichung nach dem Satz des Pythagoras an.
- 2
Berechne bei den rechtwinkligen Dreiecken die fehlenden Seitenlängen.
- 3
Berechne die Länge der Diagonalen des Rechtecks .
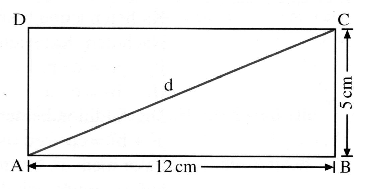 cm
cm - 4
Nach nebenstehender Zeichnung soll ein Doppeltor gebaut werden. Die Maße sind hier jeweils in angegeben. Der Querschnitt der Stäbe ist ein Quadrat mit Kantenlänge .
Berechne die Gesamtlänge an Stäben, die mindestens benötigt wird.
Beachte, wie die Profile zusammengebaut werden.

- 5
Nach nebenstehender Zeichnung soll ein Gartentor aus Vierkantprofil () gefertigt werden.
Bestimme die Gesamtlänge der benötigten Profilstäbe, wenn mit einem Verschnitt von zu rechnen ist.
- 6
Anwendung in der Physik:
Geschwindigkeitspfeile werden oft zerlegt in Horizontalgeschwidigkeit und Vertikalgeschwindigkeit .
Dabei können und je nach Richtung (rechts/links bzw. oben/unten) positiv oder negativ sein.
Beim Vektor betrachten wir hier die Pfeillänge .
Ergänze die folgende Tabelle
5
6
3
7
12
-8
0,8
15
1
17
5
25
- 7
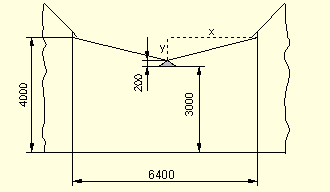
In der Mitte zwischen zwei Häusern soll an einem Spannseil eine Straßenlaterne aufgehängt werden. Das Spannseil hat genau eine Länge von .
Nachdem die Lampe angebracht wurde, hängt das Seil, wie aus nebenstehender Zeichnung zu sehen ist, etwas durch.
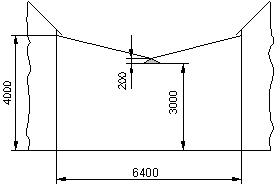
Um welche Länge wurde das Seil durch die Belastung gedehnt?
Wie viel % wird das Seil gedehnt?
- 8
Löse die folgenden Aufgaben
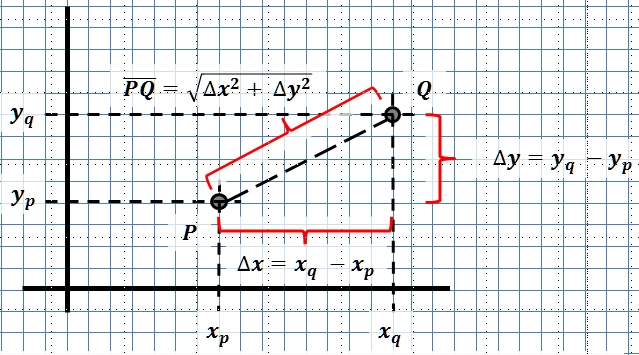
Ermittle die Formel für den Abstand der Punkte und . Mache dir die Formel anhand einer Skizze klar.
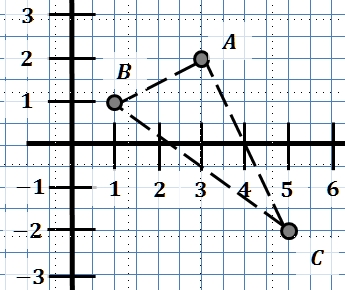
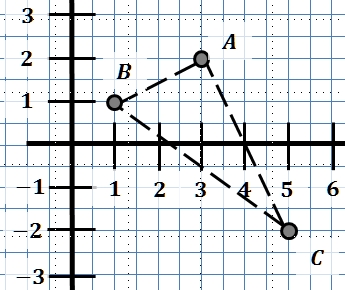
Berechne die Seitenlängen des Dreiecks mit , , .
Vom Satz des Pythagoras gilt auch die Umkehrung, d. h., gilt , so hat das Dreieck bei einen rechten Winkel. Zeige damit, dass das Dreieck aus Teilaufgabe b) bei rechtwinklig ist.
- 9
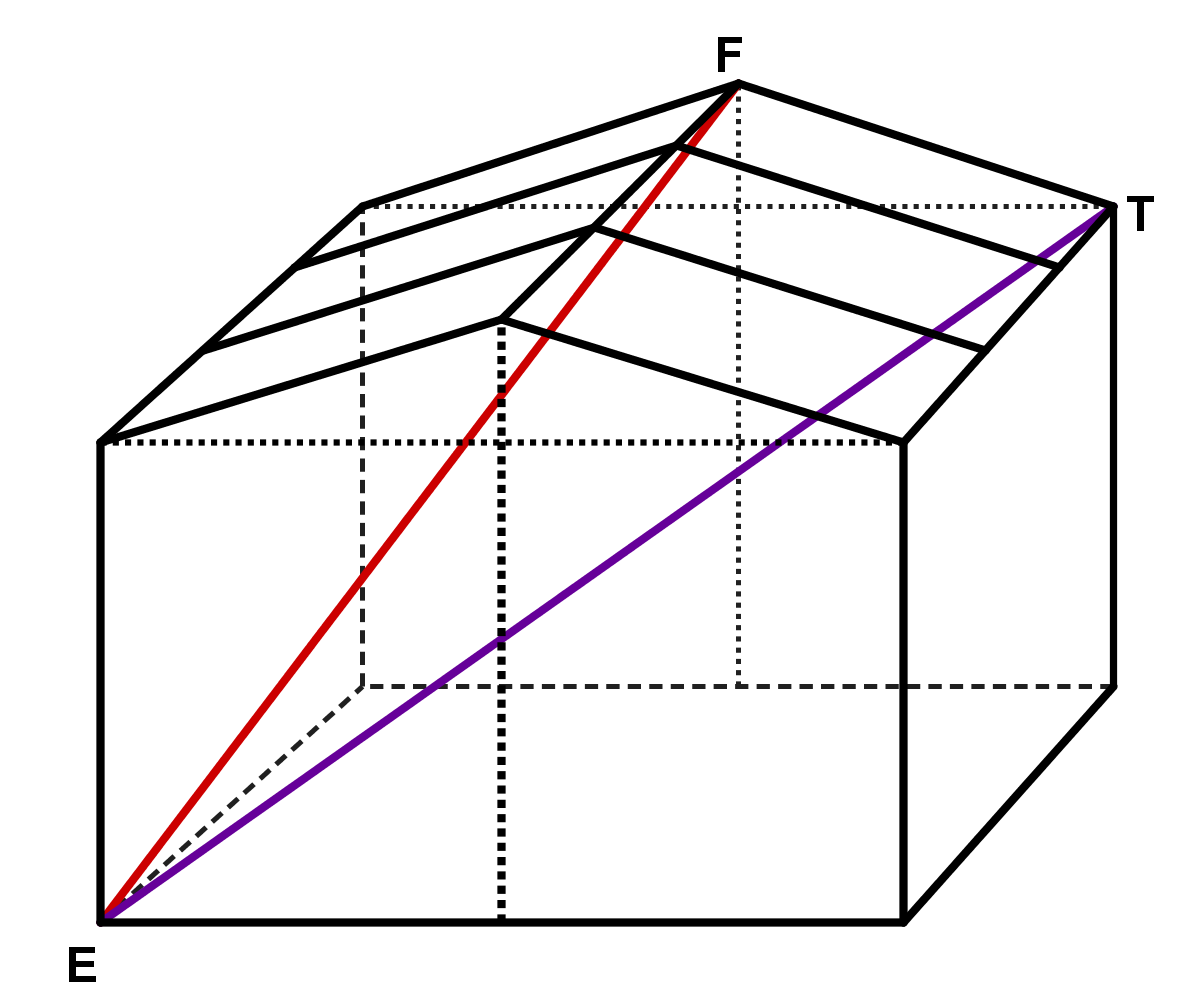
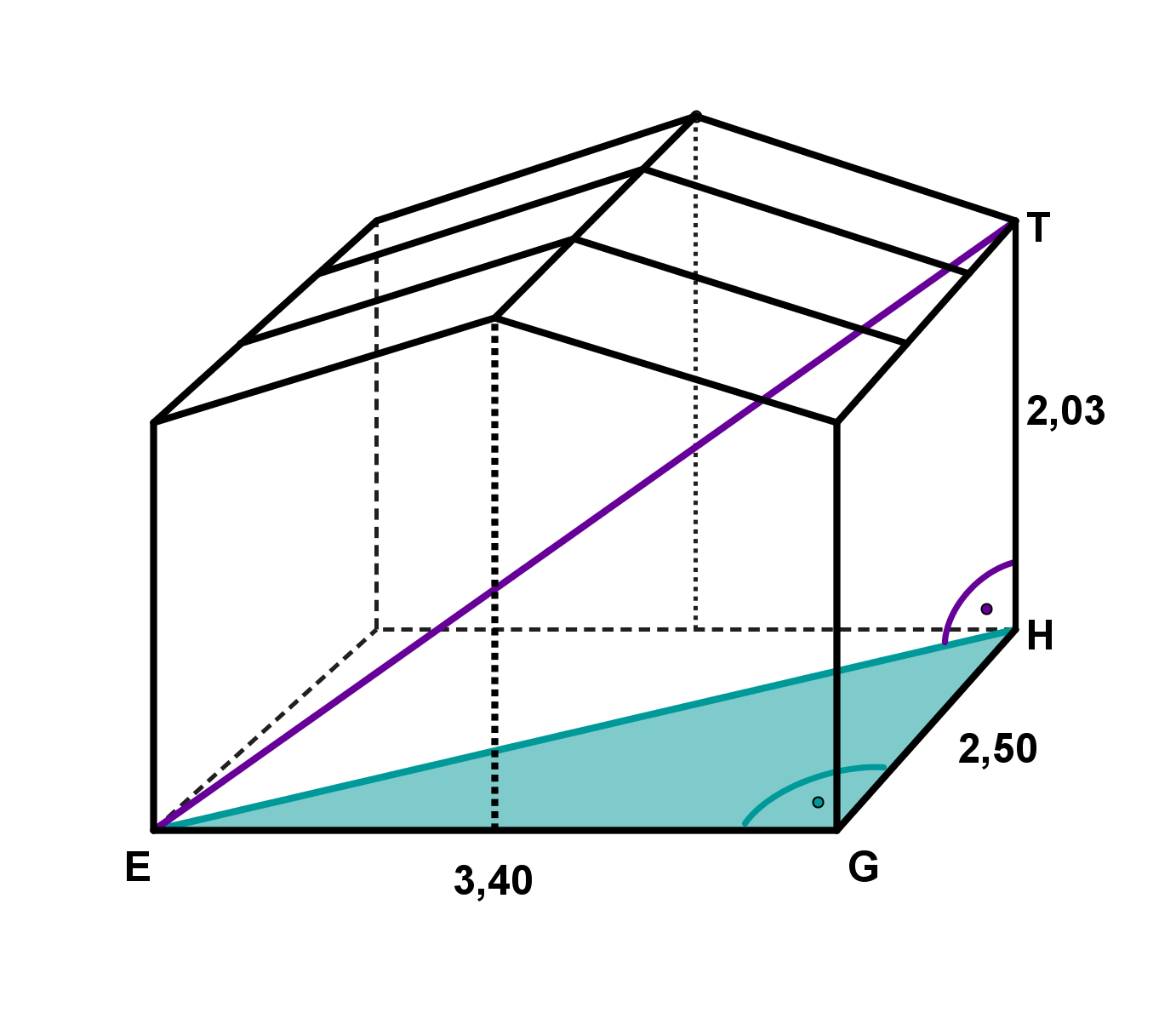
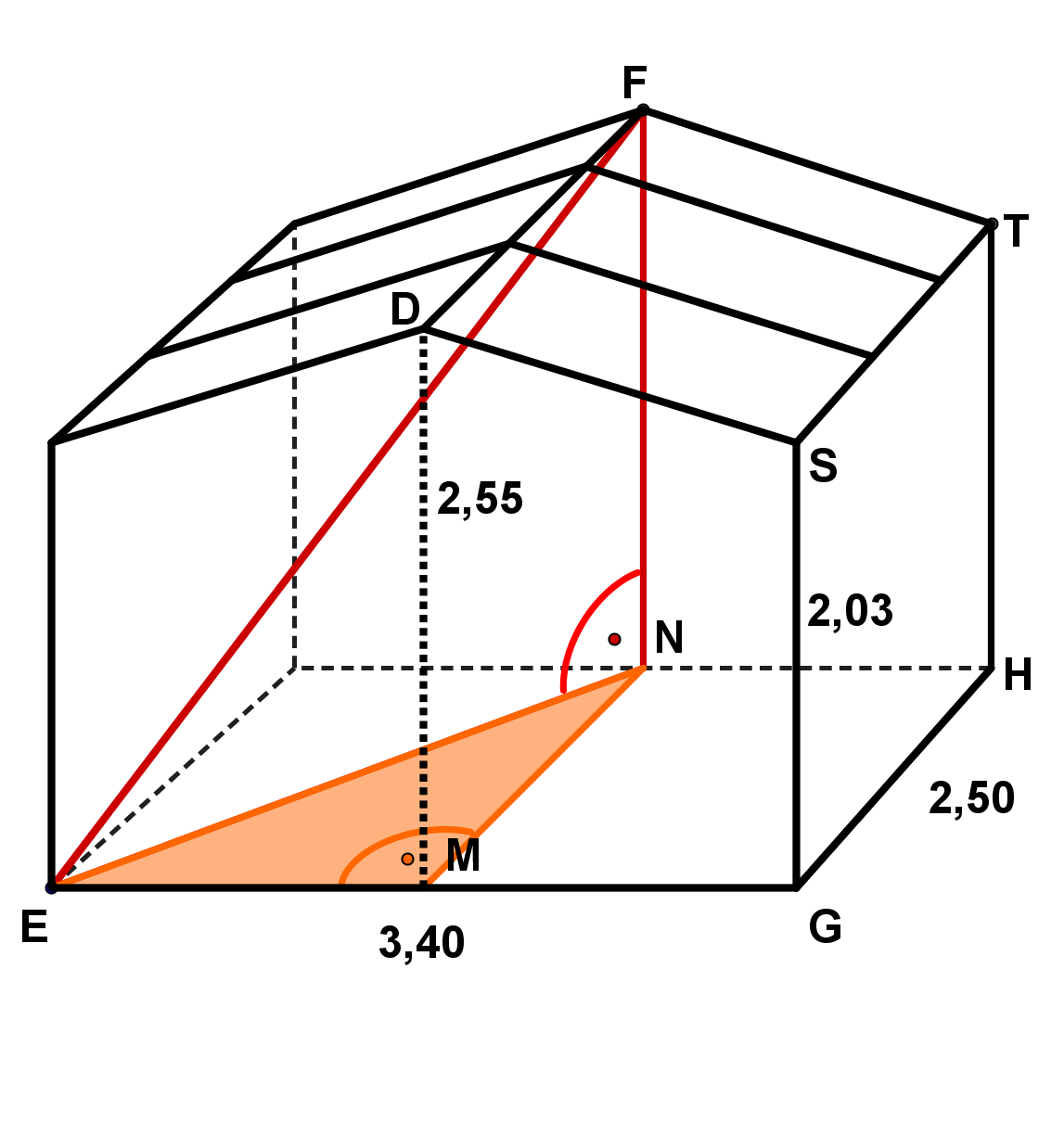
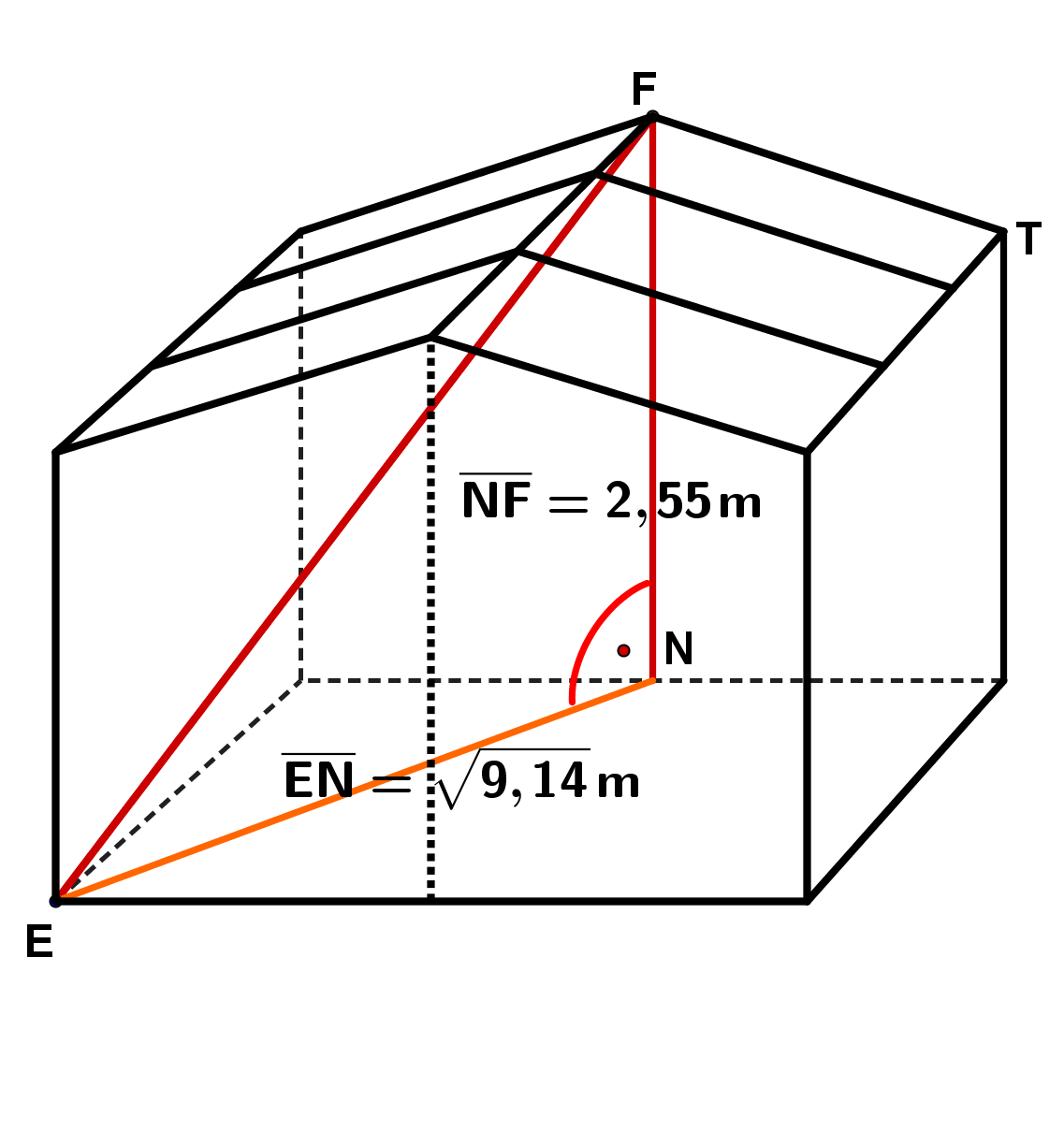
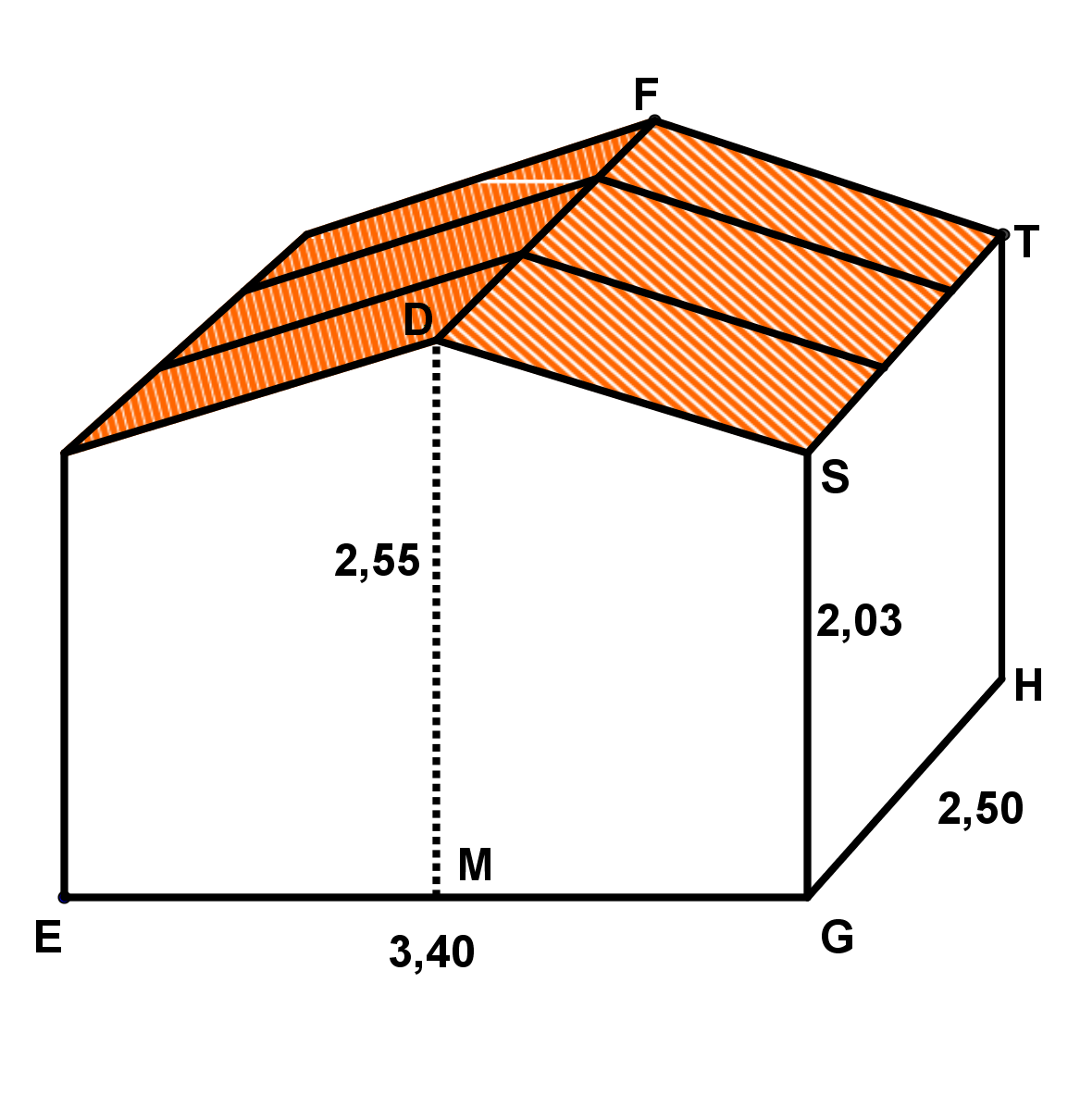
Betrachte folgendes Holzhäuschen (Maße in ):

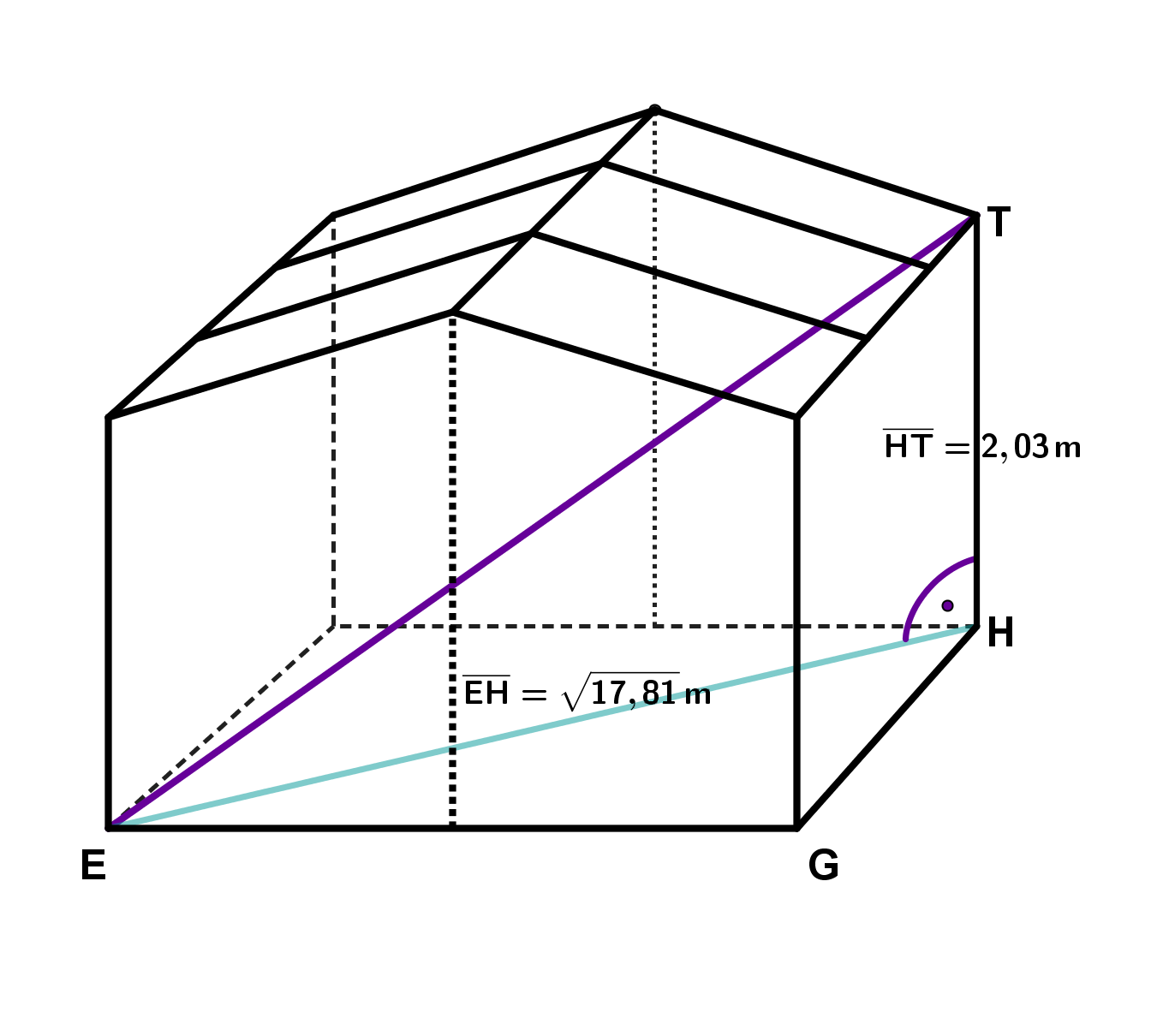
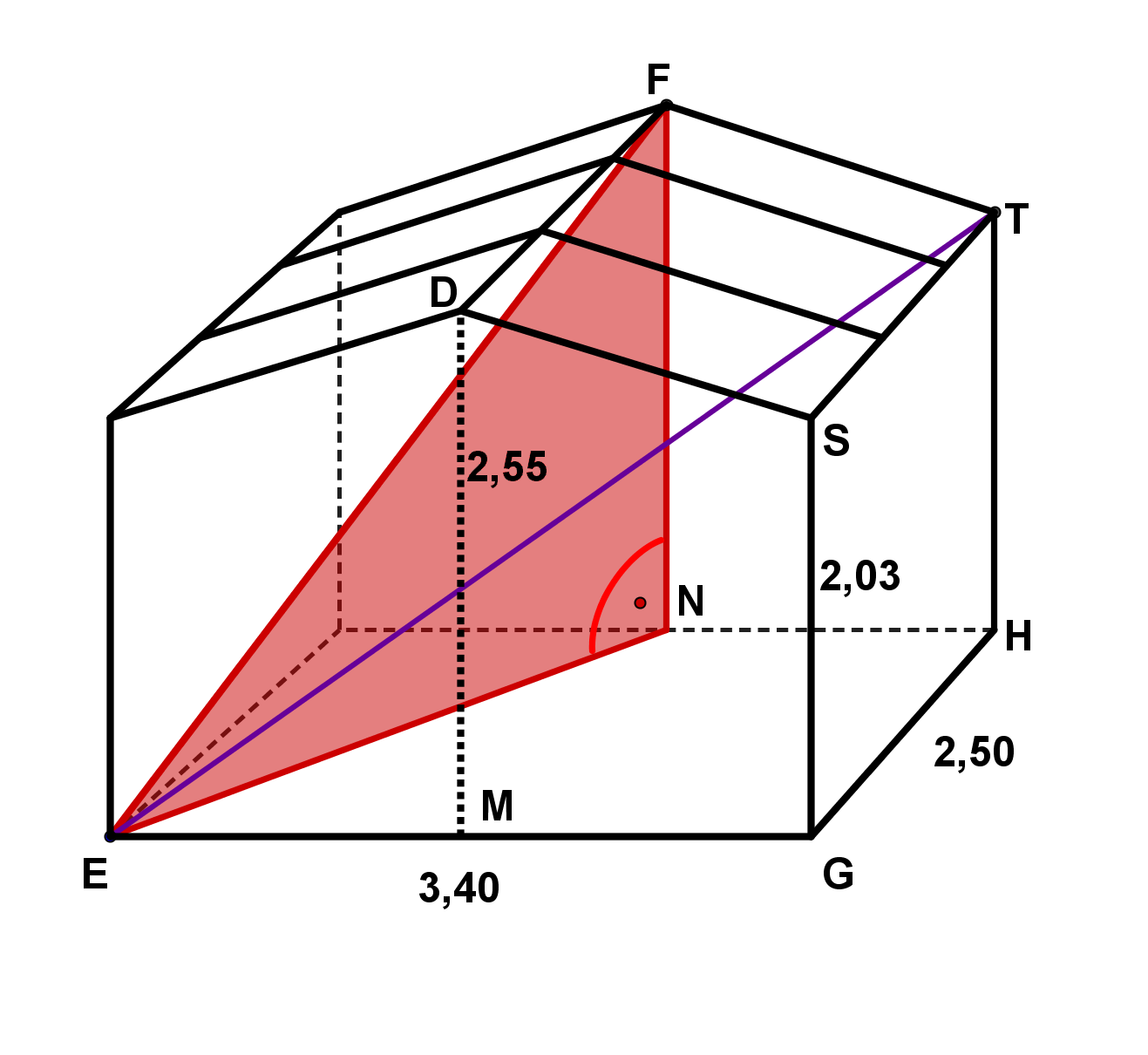
Wie lang ist der längste Faden, den eine Spinne geradlinig im Holzhäuschen spannen könnte?
Wie viel Dachfläche hat das Holzhäuschen?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?