Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Beim Einkauf bezahlt Thomas für 6 Flaschen 4,20€. Wie viel bezahlt er für 10 Flaschen? (1 Punkt)
€ - 2
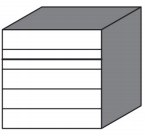
Im abgebildeten -Öltank befinden sich noch .
Zeichne auf der Vorderseite ein, wie hoch das Öl noch im Tank steht. (1 Punkt)
- 3
Welche Zahl wird hier in Potenzschreibweise dargestellt? (1 Punkt)
=
- 4
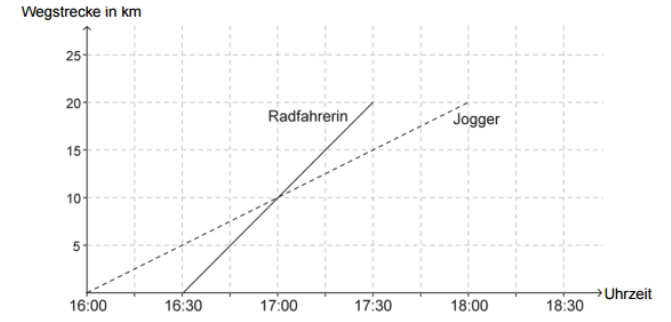
Ein Jogger und eine Radfahrerin legen den gleichen Weg zurück.Die Grafik stellt dies dar.
Ergänze die Aussagen. (1,5 Punkte)
Der Jogger startet Minuten vor der Radfahrerin.
In einer Stunde schafft die Radfahrerin Kilometer.
Nach Kilometern treffen sie sich.
- 5
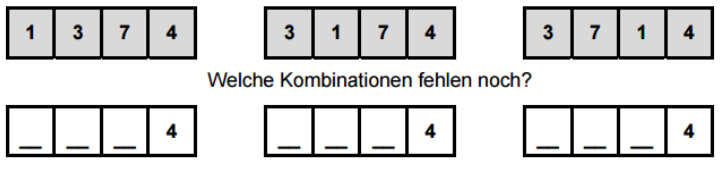
Stefanie hat ihre vierstellige Handy-PIN vergessen. Diese besteht aus den Ziffern 1,3,4 und 7, wobei jede Ziffer nur einmal vorkommt. Die 4 steht an letzter Stelle. Stefanie hat sich schon verschiedene Kombinationen überlegt:
(1,5 Punkte)
- 6
Max behauptet: „Werden bei einem Rechteck alle Seitenlängen verdoppelt, dann verdoppelt sich auch sein Flächeninhalt.“
Hat Max recht? Kreuze an. Begründe deine Entscheidung mit einem Beispiel.(1,5 Punkte)
- 7
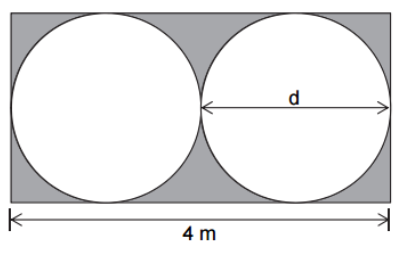
Berechne den Flächeninhalt der grau gefärbten Fläche. (2 Punkte)
Rechne mit π = 3.
- 8
Ina hat bei ihrem Handyvertrag Gesprächsminuten pro Monat frei. Ihren bisherigen Verbrauch kann sie aus folgendem Diagramm ablesen:
Wie viele Gesprächsminuten hat sie noch frei? (1 Punkt)
- 9
Dieser Becher wird gleichmäßig mit Tee gefüllt.Welches Schaubild passt zu diesem Vorgang? Kreuze an. (1 Punkt)
- 10
Löse die Aufgabe.
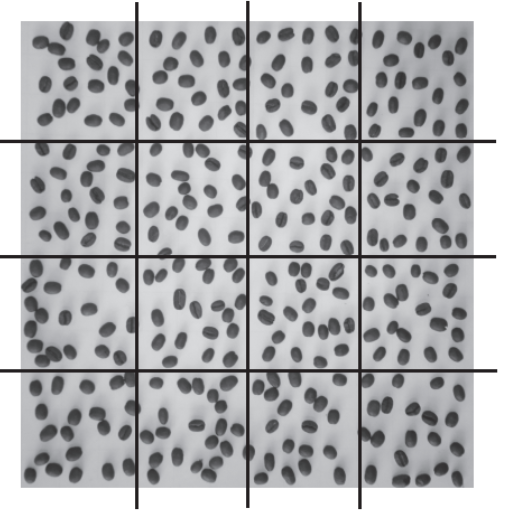
Wie viele Kaffeebohnen sind hier ungefähr abgebildet?
Gib die Anzahl an und begründe das Ergebnis.
Eine geröstete Kaffeebohne wiegt 0,2g.
Berechne, wie viel Gramm eine Packung mit 2500 gerösteten Kaffeebohnen wiegt.
Gib das Ergebnis in Gramm ein.
- 11
Ein Schüler hat eine Gleichung bearbeitet. Dabei hat er einen Fehler gemacht. (2,5 Punkte)
Unterstreiche den Fehler und verbessere nur diese Zeile.
Kreuze an, welche Regel bei folgender Umformung nicht beachtet wurde.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?