Aufgaben zu linearen Funktionen als Geraden im Koordinatensystem
Wie gut kennst du dich mit Geraden aus? Lerne mit diesen Übungsaufgaben, lineare Funktionen als Geraden zu untersuchen!
- 1
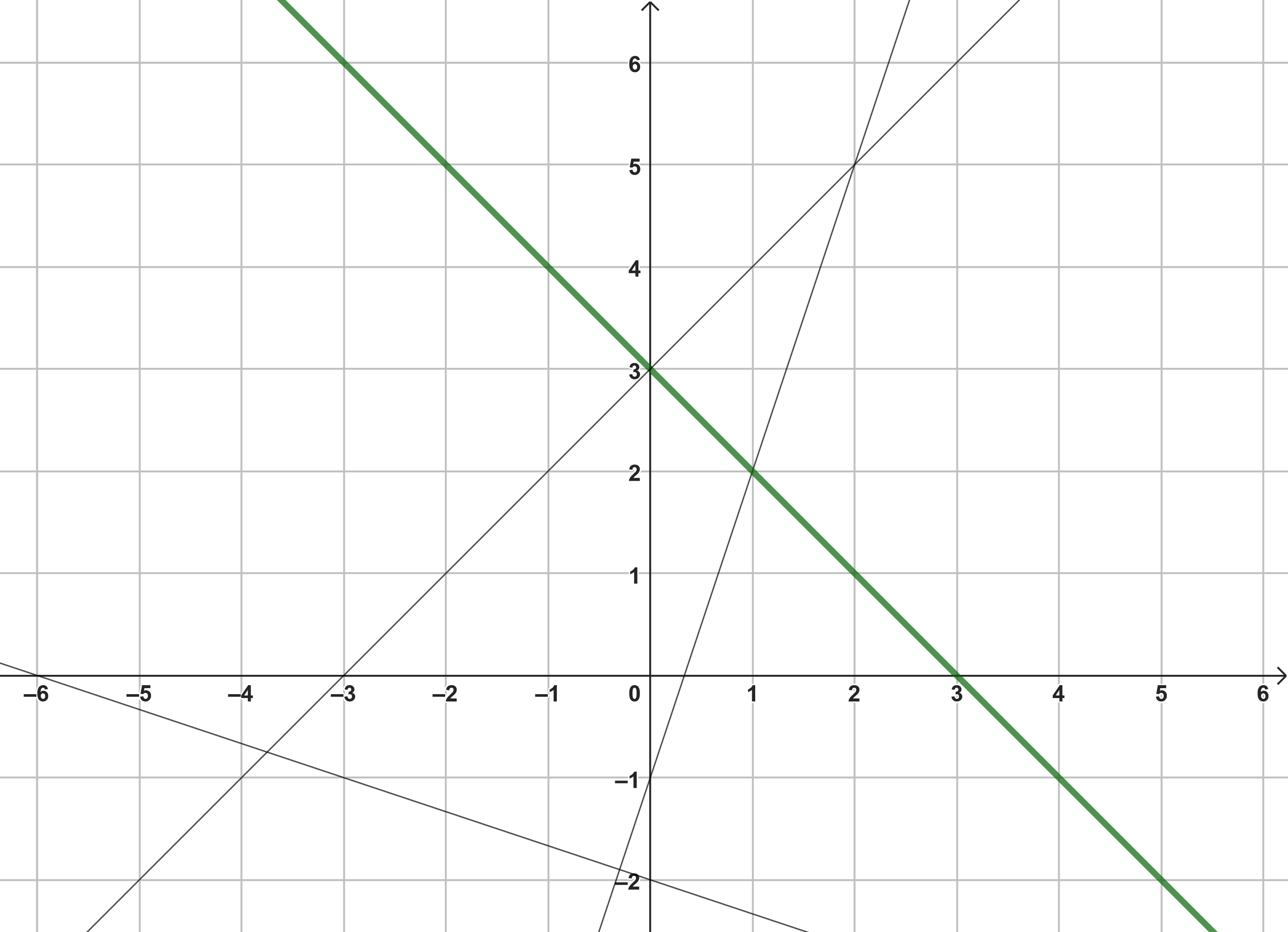
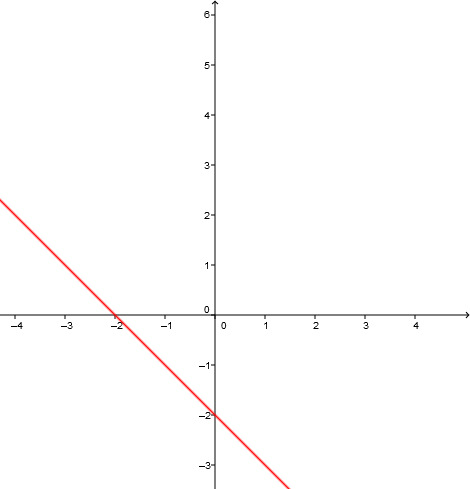
Finde die Gerade
Wähle die Gerade aus.
- 2
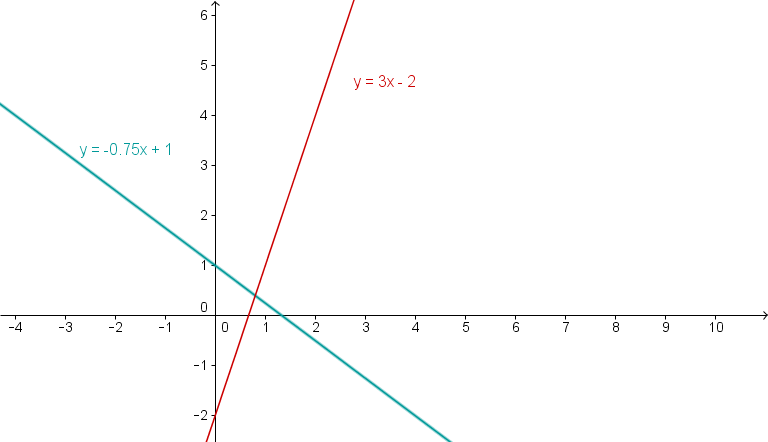
Zeichne die Geraden und in ein Koordinatensystem. Bestimme die Nullstellen und den Schnittpunkt der Geraden.
- 3
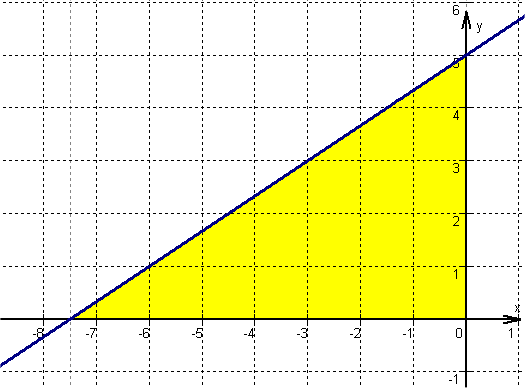
Bestimme den Flächeninhalt des Dreiecks, das von den Koordinatenachsen und der Gerade eingeschlossen wird.
Schreibe dein Ergebnis ohne Flächeneinheiten in das Antwortfeld.
- 4
Eine Gerade durch schließt mit den Koordinatenachsen ein Dreieck ein.
Für welche Steigung ist dieses Dreieck gleichschenklig?
- 5
- 6
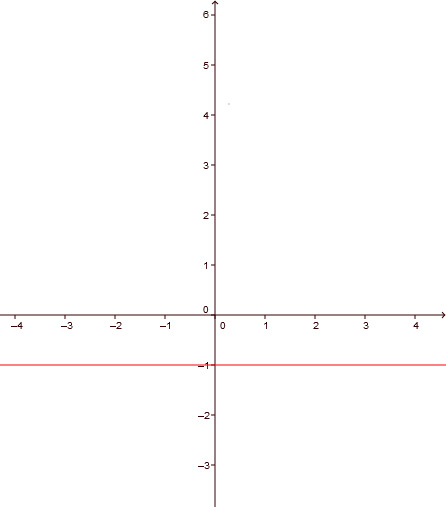
Beschreibe mit Worten die Lage der Geraden mit der Gleichung:
- 7
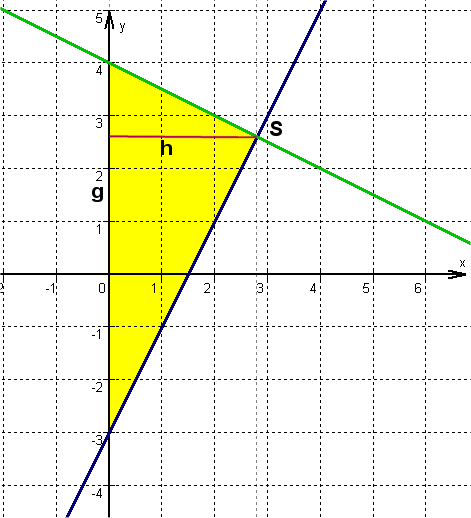
Gegeben sind die Geraden : und : .
Berechne den Schnittpunkt der beiden Geraden.
Gib ihn in der Form "(x;y)" in das Eingabefeld ein. Zum Beispiel:
Berechne die Fläche, des Dreiecks, das von und und der -Achse gebildet wird.
- 8
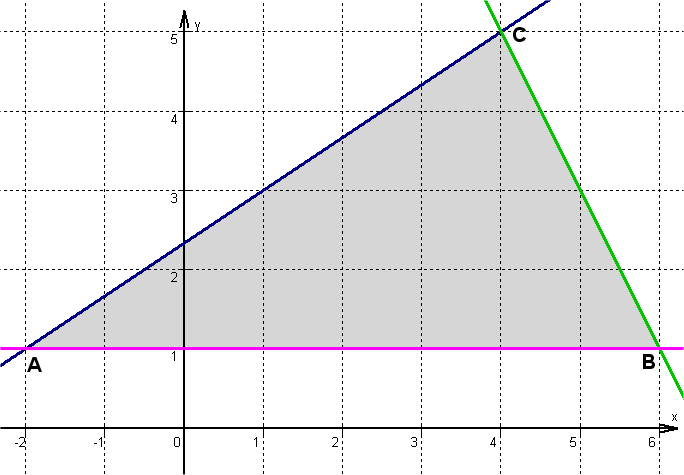
Gegeben sind die drei Punkte , und .
Stelle die Gleichung der Geraden , und auf.
Berechne den Umfang des Dreiecks .
LEBerechne den Flächeninhalt des Dreiecks .
FE
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?