Sachaufgaben zu linearen Funktionen
Hier findest du Anwendungs- und Sachaufgaben zu linearen Funktionen, die dein Verständnis testen.
- 1
Begründe, ob folgende Zuordnungen linear, proportional oder nicht-linear sind.
Anzahl der eingekauften Gurken Gesamtpreis der Gurken
Alter Körpergröße
Menge an Reis Gesamtgewicht der Schüssel mit dem Reis
Geldwert in € Geldwert in $
Lernzeit für eine Prüfung Punkte in der Prüfung
Seitenlänge eines Quadrats Fläche des Quadrats
Anzahl der Schokoriegel Anzahl der durch die Schokoriegel zugeführten Kalorien
Anzahl der Getränke bei einem Diskobesuch Kosten für einen Diskobesuch
(Alle Getränke kosten gleich viel.)
- 2
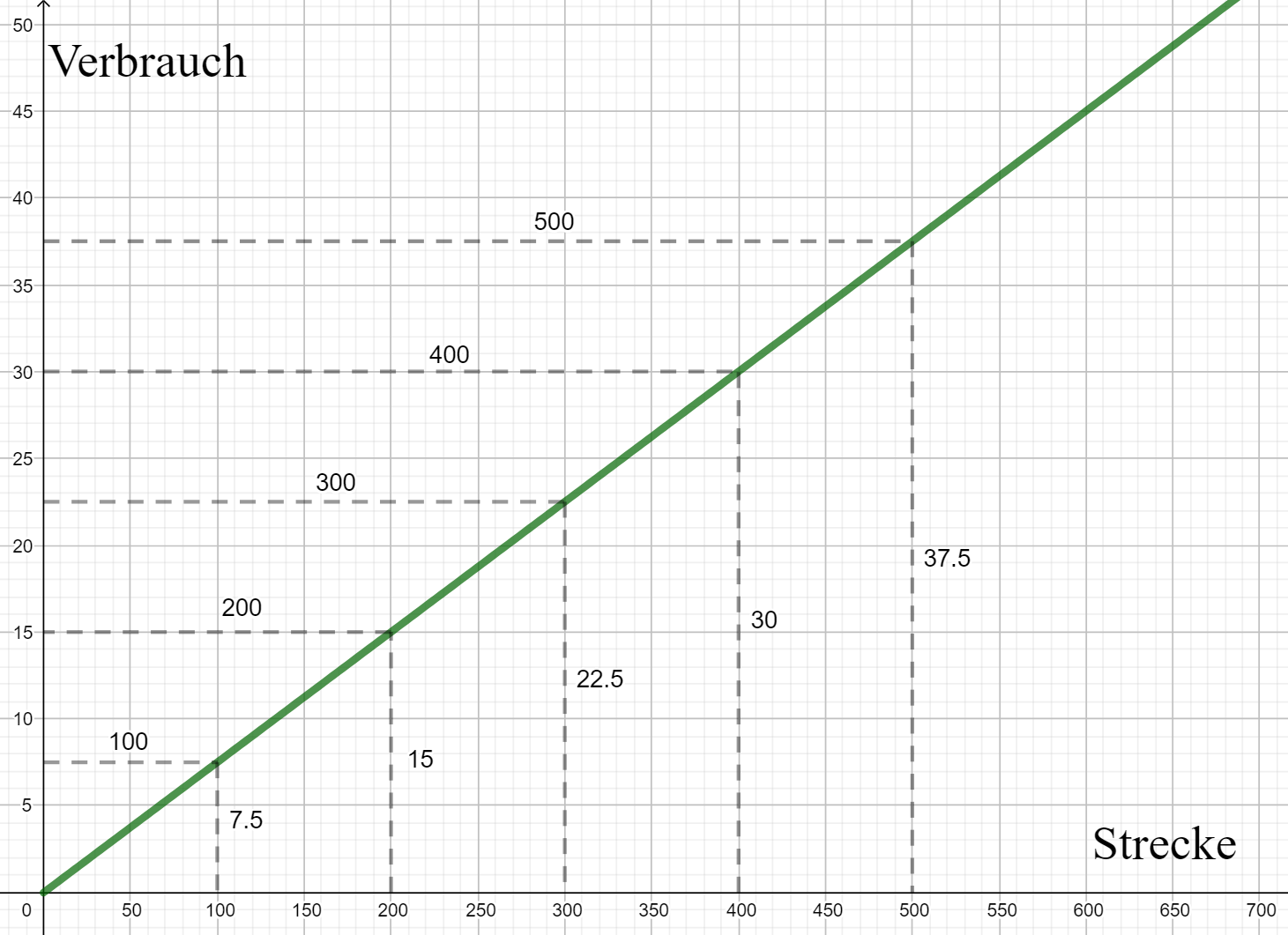
Ein Auto besitzt einen Treibstoffvorrat von 56 Liter Benzin. Auf 100km verbraucht es 7,5 Liter.
Erstelle eine Tabelle für den Verbrauch in Litern. Wähle eine Strecke von 0km bis 600km (100km Abstand)
Stelle den Zusammenhang graphisch dar.
Nach wie viel km wäre der Benzinvorrat aufgebraucht? Bei einem Benzinvorrat von 5L soll der Fahrer tanken gehen. Nach wie viel km muss es erfolgen?
- 3
Herr Breuer hat einen Handyvertrag mit folgenden Konditionen abgeschlossen:
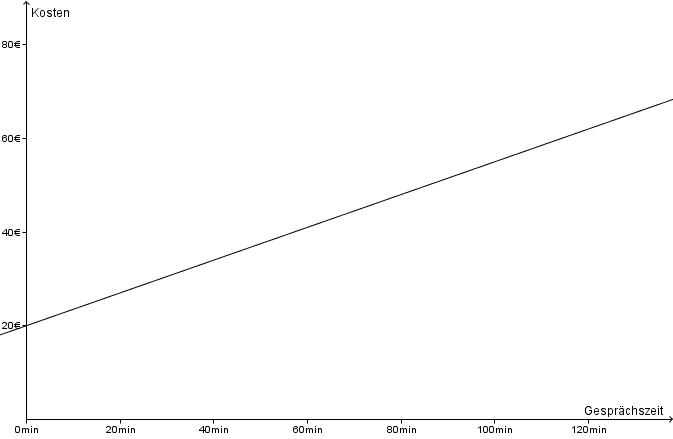
Monatliche Grundgebühr 20€, Telefonkosten pro Minute 0,35€.
Wie hoch ist seine Monatsrechnung, wenn er 40, 80 oder 120 Minuten telefoniert?
Erstelle einen Term für die monatlichen Kosten in Abhängigkeit von der Gesprächsdauer in Minuten.
Stelle den Zusammenhang graphisch dar.
- 4
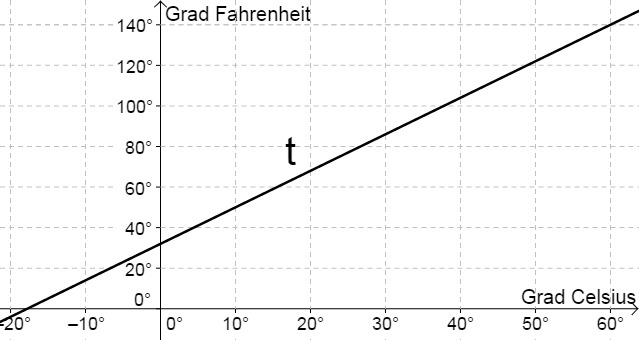
Folgende Tabelle gibt für einige Temperaturen den Wert in Grad Celsius (°C) und Grad Fahrenheit (°F) an.
Temperatur in Celsius
Temperatur in Fahrenheit
-10°
14°
0°
32°
20°
68°
60°
140°
Es handelt sich um einen linearen Zusammenhang. Zeichne mit der Tabelle einen Graphen (x-Achse=Grad Celsius, y-Achse=Grad Fahrenheit) und gib eine Formel an, mit der man Grad Celsius in Grad Fahrenheit umrechnet.
- 5
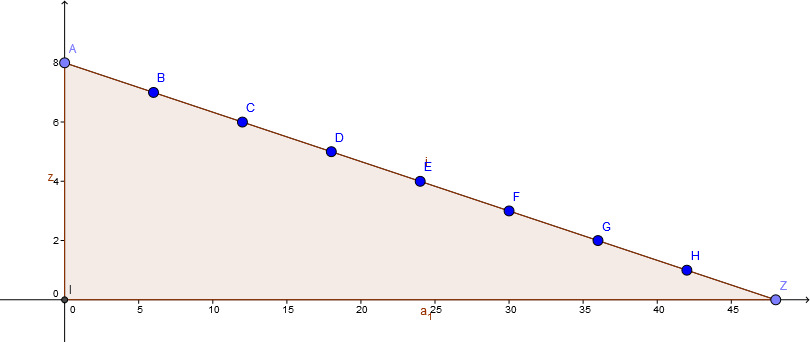
Ein Lieferwagen, der mit 1,2 t beladen ist, transportiert x Stücke zu je und y Kisten zu je .
Stelle den Zusammenhang zwischen x und y in einem Diagramm dar.
Welche Punkte sind möglich, wenn der Lieferwagen maximal 1,2 t beladen ist?
- 6
Eine Zeitschrift, die zum Preis von € zu kaufen ist, hat eine Auflage von Exemplaren. Mit Hilfe der Marktforschung stellt der Verlag fest, dass sich die Auflage bei einer Preissenkung um € pro Zeitschrift um Exemplare erhöhen lässt, bei einer Preiserhöhung von € verliert man Käufer.
Berechnen Sie den Preis bei einer Auflage von 140 000 Exemplaren.
€Welche Verkaufszahlen kann der Verlag erwarten, wenn er den Preis der Zeitschrift auf 1,50€ senkt?
Stück
- 7
“Es ist eine ganz langsam verlaufende völlig undramatische Trennungsgeschichte, Schritt für Schritt: Zwei Zentimeter pro Jahr entfernt sich die Eurasische Kontinentalplatte von der Nordamerikanischen Platte. Würde man heute dem Kurs von Kolumbus folgen, der von Andalusien in die Neue Welt fuhr, müsste man circa ___ Meter mehr an Strecke überwinden. Das bringt einen Kapitän von heute auf der mehr als 6.000 Kilometer langen Fahrt zwischen Europa und Amerika wohl kaum aus der Ruhe.”
Um wie viele Meter hat sich die Strecke verlängert?
mIn wie vielen Jahren kommen weitere 5 Meter Distanz zwischen den Kontinentalplatten hinzu?
Jahren
- 8
Ein Patient erhält eine Infusion. Eine volle Flasche enthält dabei 40ml Infussionsflüssigkeit. Die Tropfgeschwindigkeit wird so eingestellt, dass 3ml der Flüssigkeit pro Minute durchlaufen. Sobald weniger als 5ml in der Flasche sind, muss diese ausgetauscht werden. Nach welcher Zeit ist dies notwendig?
- 9
Jonathan und Hannes steigen auf die Zugspitze. Jonathan beginnt seine Wanderung auf Meereshöhe (), Hannes startet auf dem Zugspitzplatt (). Beide steigen mit pro auf. Der Funktionsterm, mit dem Jonathans Aufstieg beschrieben wird, ist Entscheide, welcher Funktionsterm zum Aufstieg von Hannes passt!
- 10
Max und Jana machen einen Ausflug in den Wildpark "Tierisches Glück" in Tierhausen. Der Eintritt in den Wildpark kostet dabei . Im Wildpark hat man an jedem Gehege zusätzlich die Möglichkeit für ein spezielles Tierfutter zu kaufen, um damit die Tiere zu füttern.

(a) Bestimme wie viel Max und Jana für ihren Ausflug insgesamt ausgeben müssen, wenn sie im Wildpark , bzw. Tierfutter kaufen wollen. Erstelle aus diesen Werte eine Wertetabelle.
(b) Erstelle einen Term für die Kosten des Ausflugs in Abhängigkeit der Anzahl der Tierfutter, die Max und Jana kaufen.
(c) Stelle den Zusammenhang aus Teilaufgabe (b) graphisch dar.
(d) Max und Jana haben zu Beginn ihres Ausflugs dabei. Lese aus dem Graphen ab, wie viel Tierfutter die beiden damit kaufen können.
- 11
Die NASA ist eine Luft- und Raumfahrt Behörde, die Raketen in das Weltall befördert. Dafür muss zunächst (einmalig) eine Startrampe gebaut werden, die die NASA eine Milliarde US-Dollar kostet. Der Bau einer Rakete selbst kostet dagegen eine halbe Milliarde Dollar.
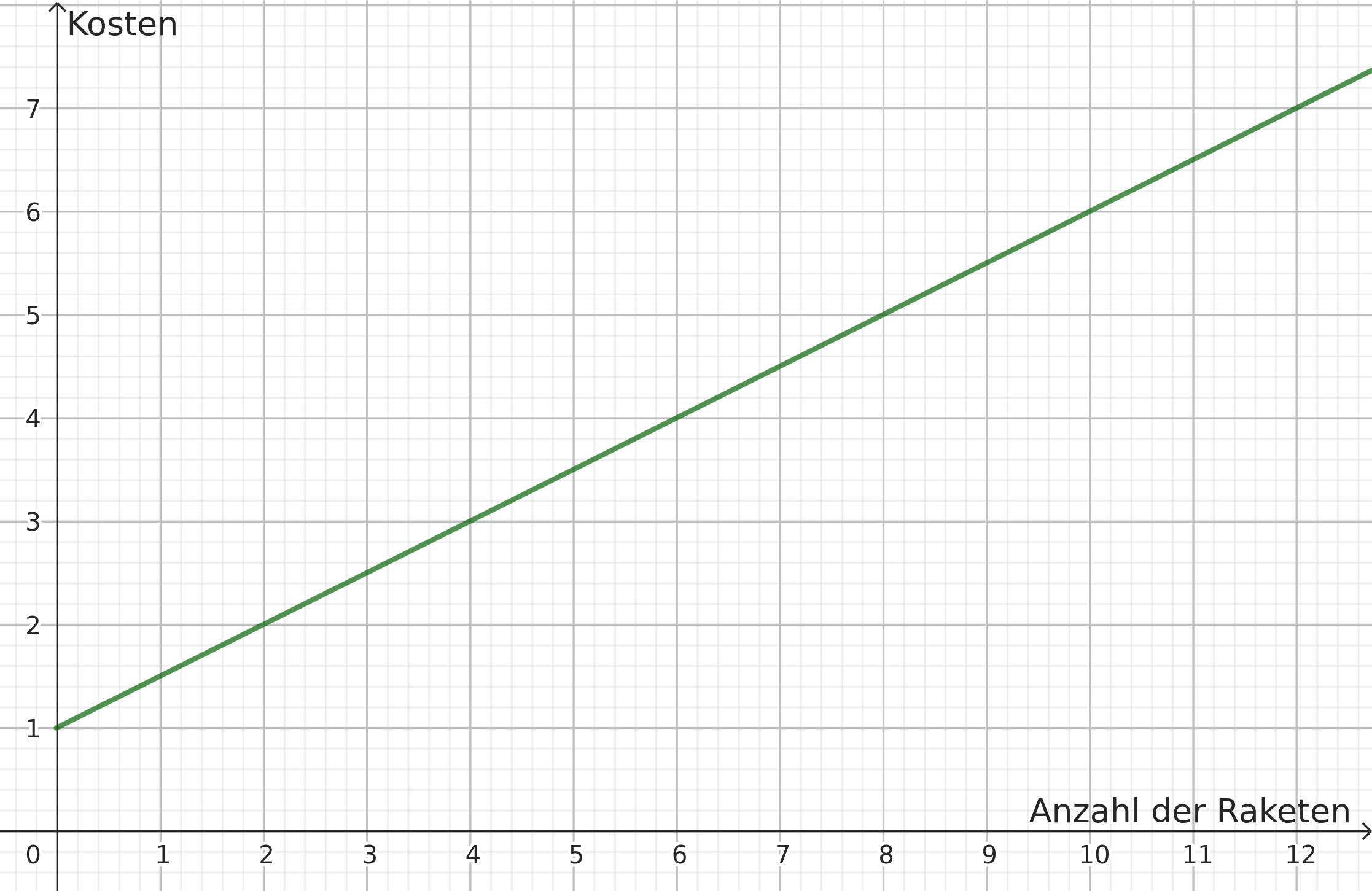
Berechne, wie viel die NASA insgesamt ausgibt, wenn sie 4, 6 bzw. 10 Raketen ins All schießt. Fertige daraus eine Wertetabelle an.
Stelle einen Term auf, der die Gesamtkosten der NASA in Abhängigkeit der Raketen angibt, die ins All gebracht werden.
Stelle den Zusammenhang aus der Teilaufgabe (b) grafisch dar. Verwende als Skalierungseinheit auf der y-Achse eine Milliarde US-Dollar.
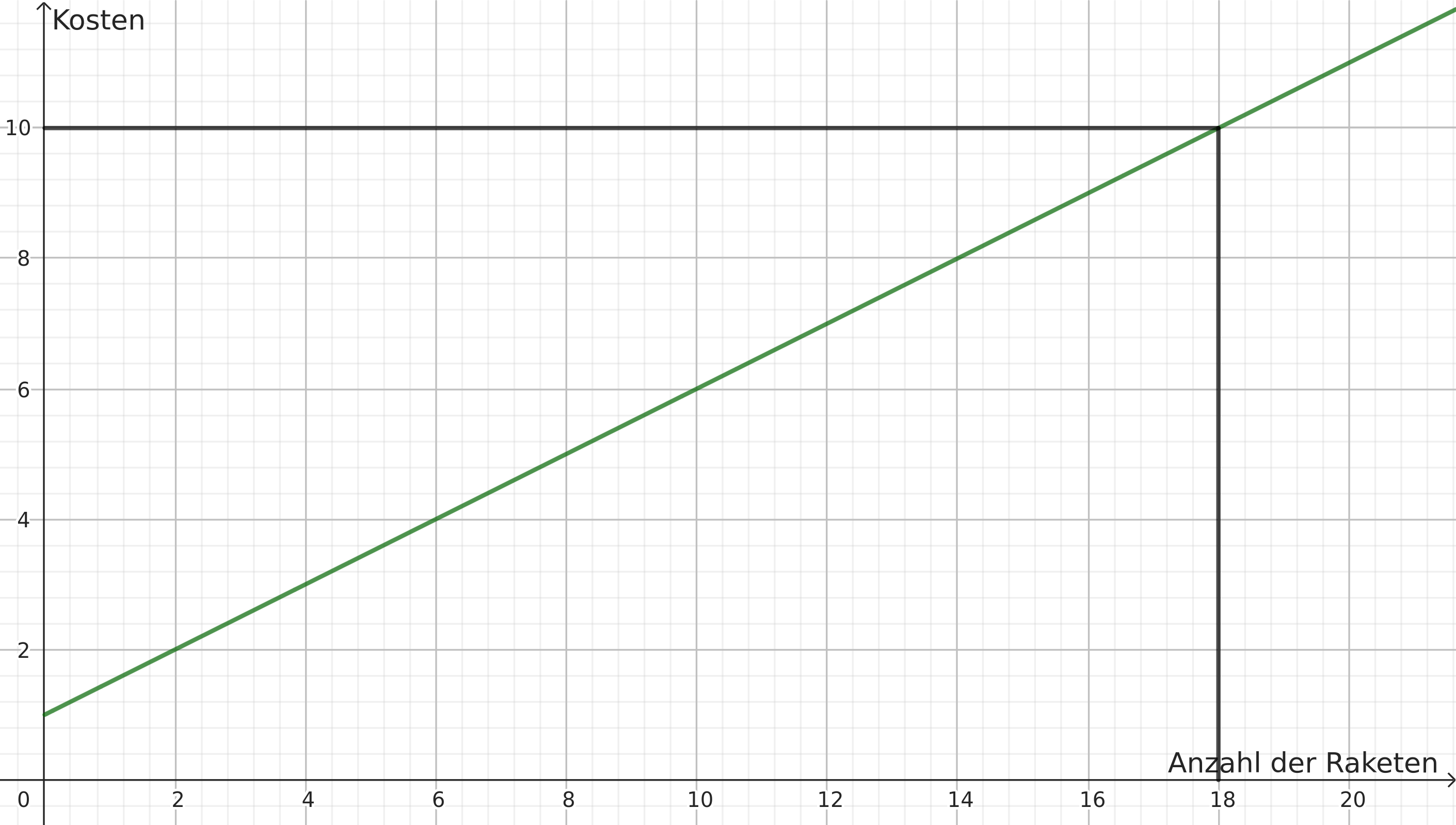
Bestimme wie viele Raketen die NASA mit 10 Milliarden US-Dollar ins All schicken kann.
- 12
In einer Höhe von 5000 m über Trübsalhausen ziehen dunkle Wolken auf und es fängt an zu regnen. Die Regentropfen fallen in einer Minute 500 m weit nach unten.

Berechne, welche Höhe die Regentropfen nach einer, zwei bzw. fünf Minuten über dem Boden haben. Fertige daraus eine Wertetabelle an.
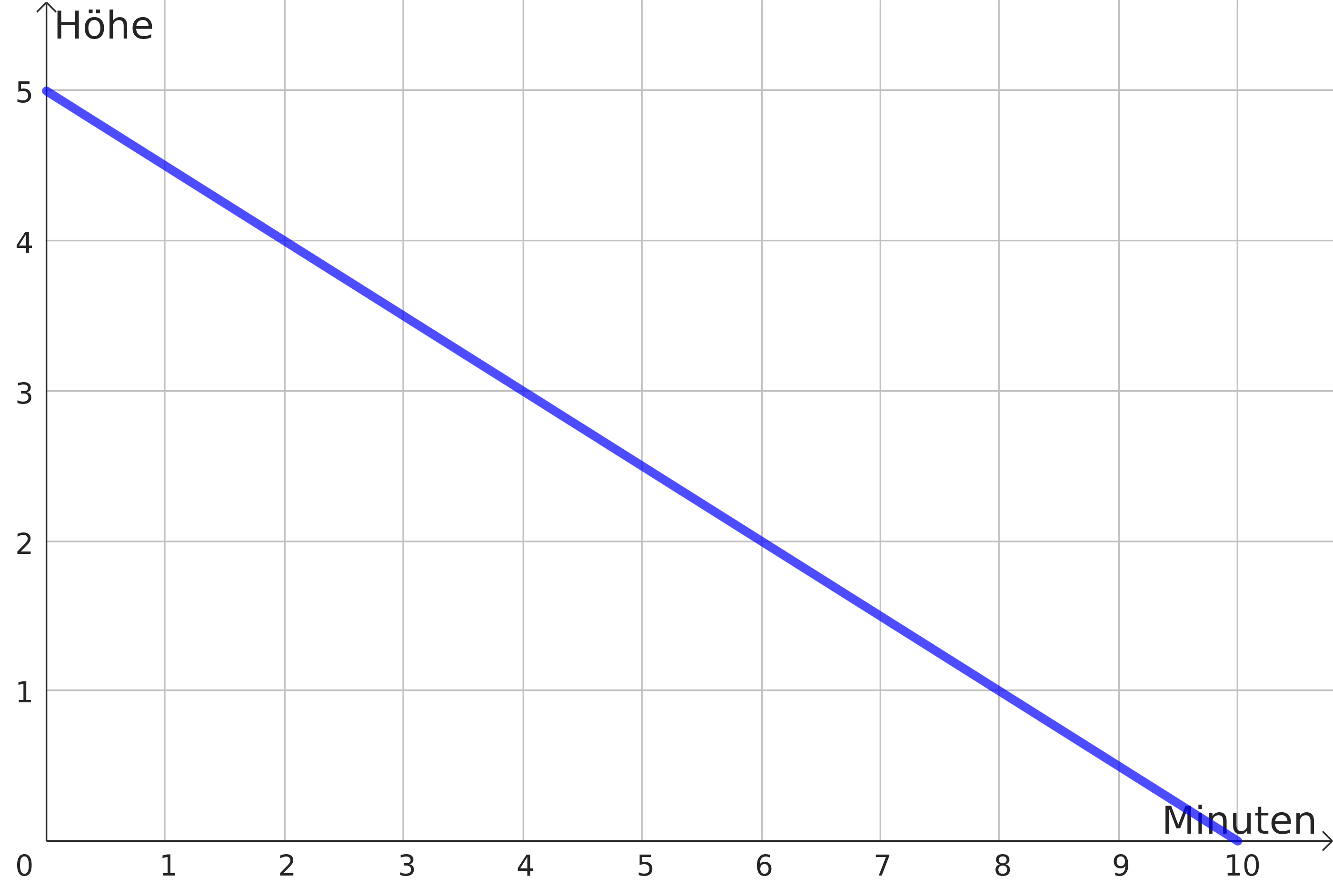
Stelle einen Term auf, der die Höhe der Regentropfen (Einheit ) in Abhängigkeit der Fallzeit in Minuten angibt. Du kannst dabei vernachlässigen, dass die Tropfen nach der Ankunft am Boden nicht mehr weiter fallen.
Zeichne den Zusammenhang aus Teilaufgabe (b) in ein Koordinatensystem.
Bestimme, nach wie vielen Minuten die Regentropfen am Boden angekommen sind.
- 13
Waldstetten ist bekannt für seine vielen grünen Laubbäume. Wie alle Laubbäume verlieren aber auch diese im Herbst ihre Blätter. Im Sommer hängen an einem Baum noch Blätter. Im Herbst, verliert er pro Woche Blätter.

(Bildquelle: https://pixnio.com/de/landschaften/herbst/blaetter-im-herbst-gelblich-blaetter-rote-baeume-laub-herbst-herbst-blaetter-baeume)
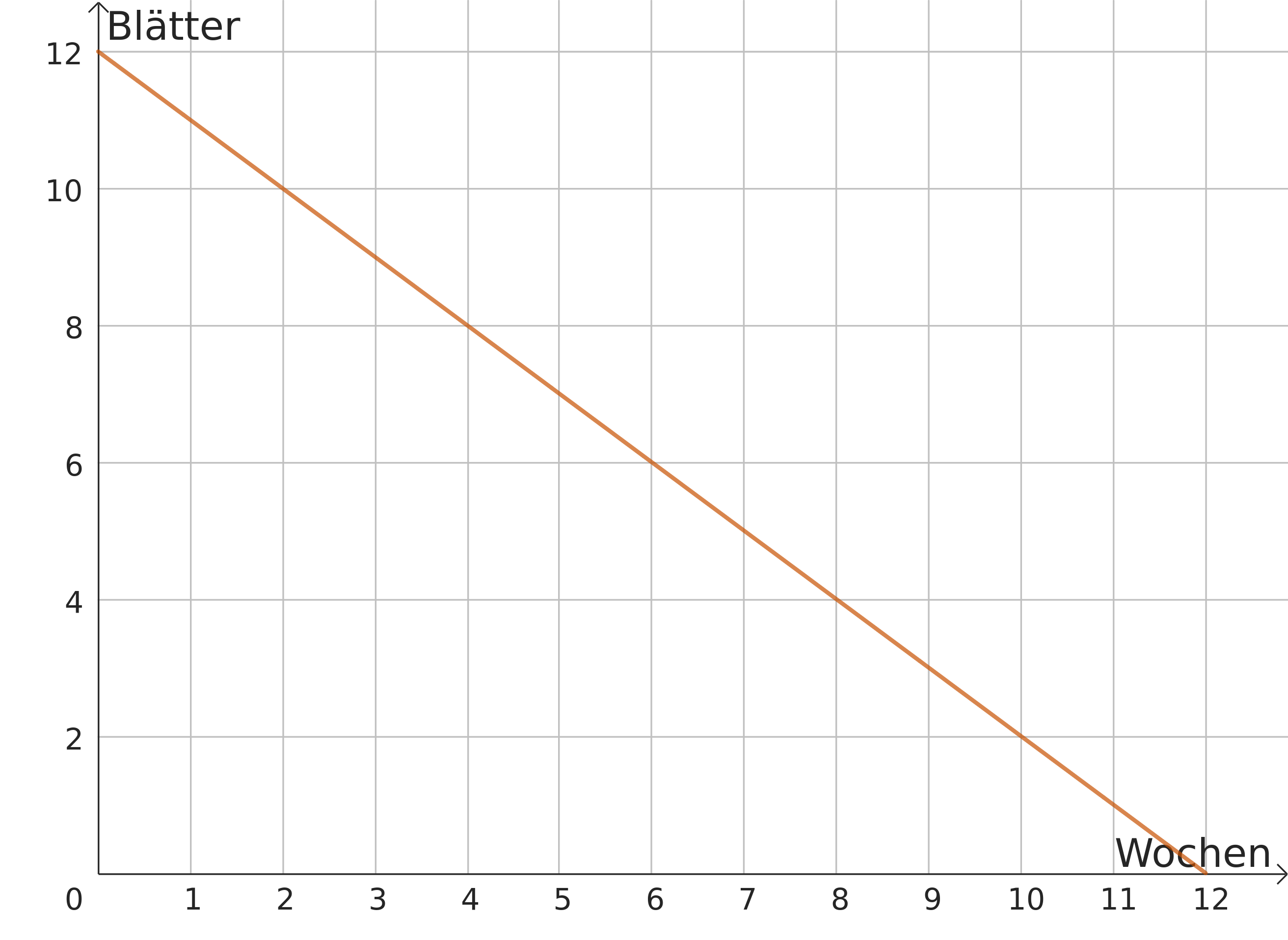
Stelle einen Term auf, der die Anzahl der Blätter eines Baumes in Abhängigkeit der seit Beginn des Herbstes vergangen Wochen angibt.
Zeichne diesen Zusammenhang in einem Koordinatensystem. Trage auf der -Achse die Anzahl der Blätter (mit Einheit Blätter) und auf der -Achse die Anzahl der vergangenen Wochen auf.
Berechne, wie viele Blätter nach bzw. Wochen noch am Baum hängen.
- 14
In einen leeren Whirlpool wird Wasser gefüllt. Pro Minute fließen Wasser in den Pool.

Ergänze die Tabelle:
Zeit (in min)
0
1
2
5
8,2
15
25
Wassermenge (in Litern)
Die Funktion ist durch die Zuordnungsvorschrift: Zeit Wasservolumen gegeben.
Übertrage die Punkte der Funktion in ein Koordinatensystem und zeichne den Graphen der Funktion .
Wie lautet die Funktionsgleichung, die die zugeflossene Wassermenge in Abhängigkeit von der Zeit angibt?
In den Whirlpool dürfen maximal Liter Wasser eingefüllt werden.
Wie muss der Graph aus Aufgabe an diese neue Information angepasst werden?
Lies ab und berechne, nach welcher Zeit (in Minuten) der Wasserzulauf abgestellt werden muss.
- 15
Eine Kerze ist anfangs lang. Wenn sie brennt, wird sie in jeder Stunde um kürzer.

Wie viele Stunden dauert es, bis die Kerze ganz abgebrannt ist?
StundenZeichne den Graphen der Funktion :
Brenndauer Länge .
Notiere die Funktionsgleichung.
Berechne die Länge der Kerze nach bzw. Stunden. Überprüfe deine berechneten Werte anhand des Graphen.
Berechne, nach wie viel Stunden die Kerze nur noch lang ist.
Stunden
- 16
Ein Wasserversorger berechnet pro Wasser (Verbrauchskosten). Zusätzlich muss der Kunde eine monatliche Grundgebühr in Höhe von 6 € bezahlen.
Monatlich ergeben sich die Gesamtkosten aus der Summe der Verbrauchskosten und der Grundgebühr.

Ergänze die Tabelle.
Wasserverbrauch (in m³)
0
1
2
3
7,8
15
20
Verbrauchskosten (in €)
Gesamtkosten (in €)
Zeichne den Graphen der Funktion :
Wasserverbrauch (in ) Gesamtkosten (in €)
Bestimme auch die Funktionsgleichung.
- 17
Ziehe die richtige Gleichung in das Ablagefeld.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?