Aufgaben zu Potenz- und Wurzelfunktionen
Wie gut kennst du dich aus? Hier findest du Übungsaufgaben zu den Potenz- und Wurzelfunktionen.
- 1
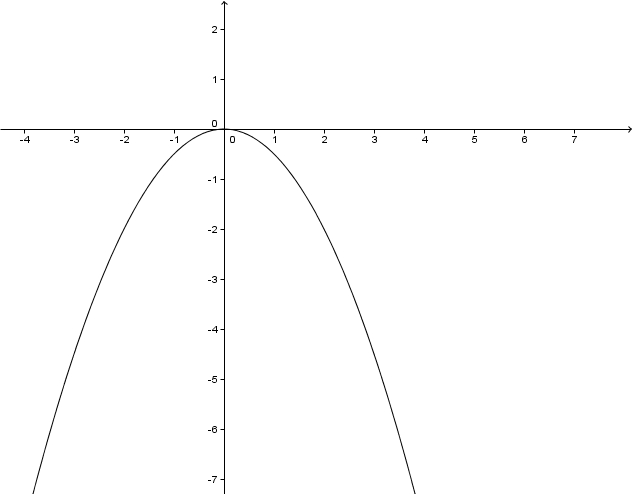
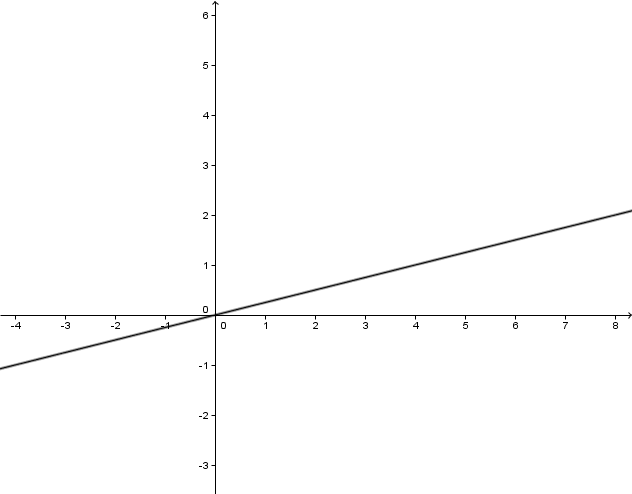
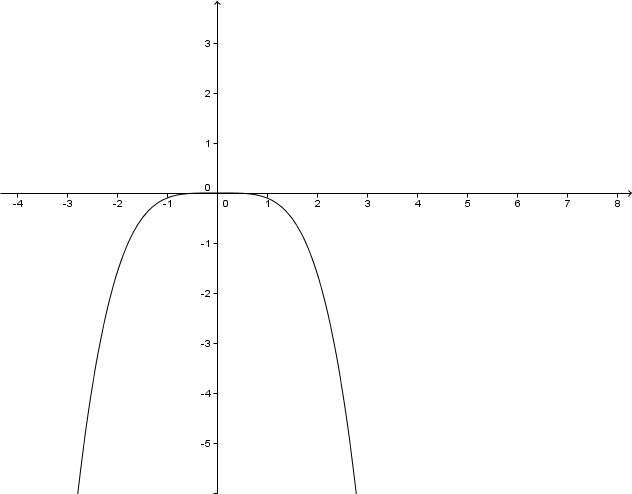
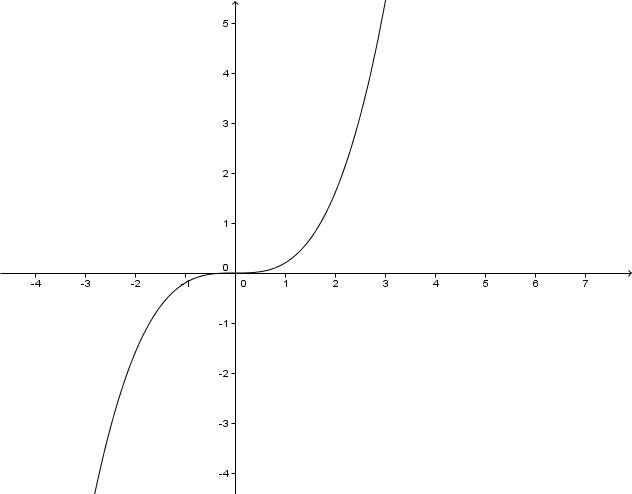
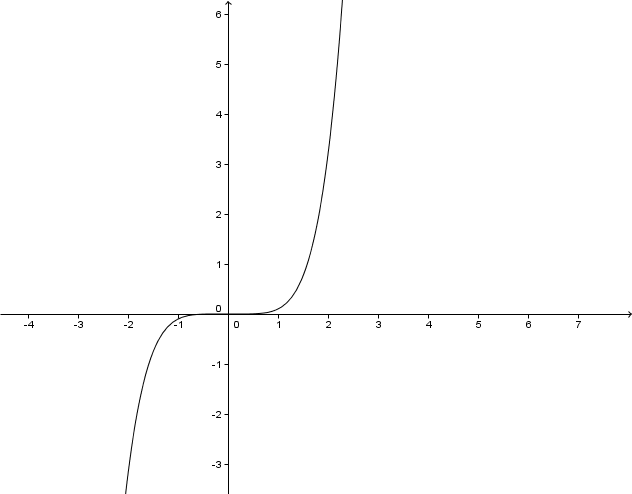
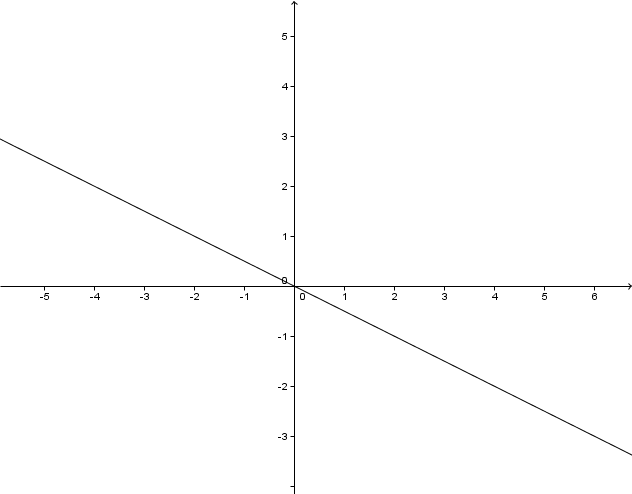
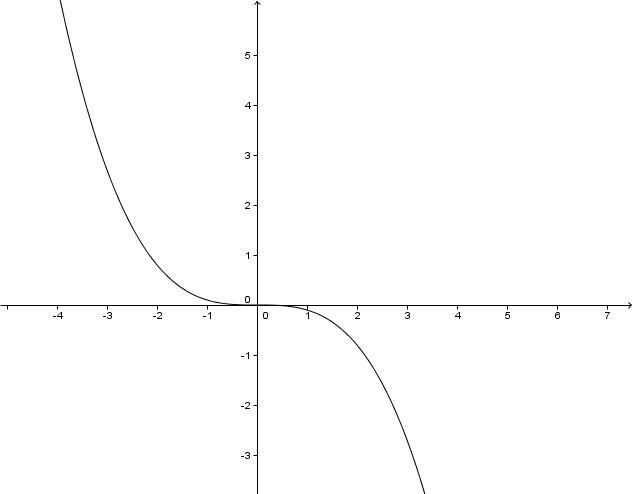
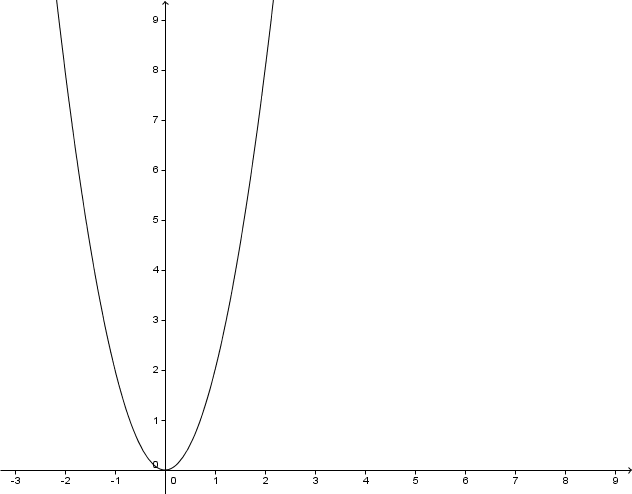
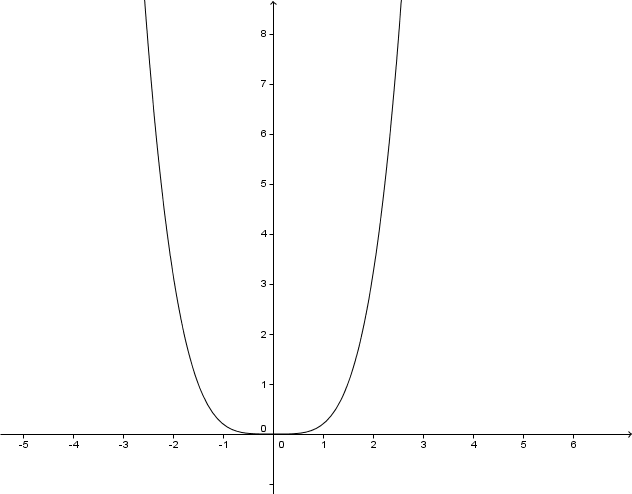
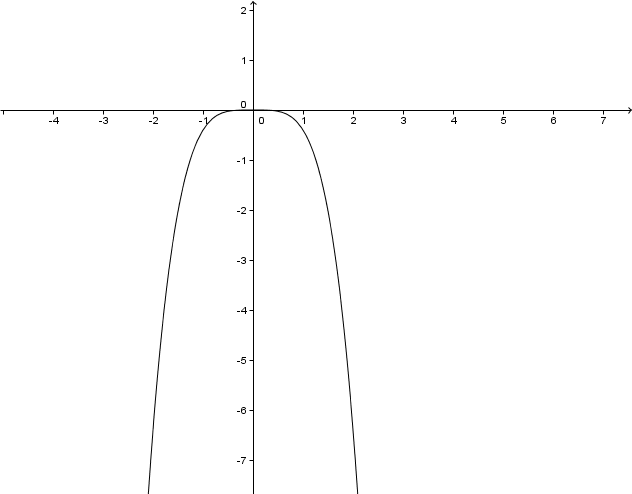
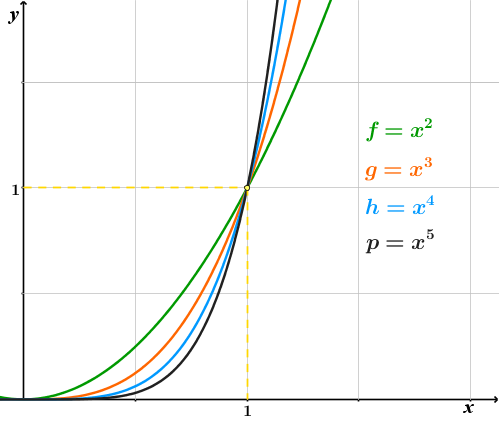
Betrachte die Graphen der Potenzfunktionen im . Quadranten. Für - Werte zwischen und liegt der Graph einer Potenzfunktion höheren Grades unterhalb des Graphen einer Potenzfunktion niederen Grades. Für ist das genau umgekehrt.
Begründe dieses Verhalten.
- 2
Der Graph der Potenzfunktion 3.Grades soll um 2 Einheiten nach links und anschließend um 3 Einheiten nach oben verschoben werden. Gib die Funktionsgleichung für den verschobenen Graphen an.
- 3
Bestimme die Symmetrie und den Verlauf der Graphen folgender Potenzfunktionen und gib jeweils die Wertemenge und den Grad an.
- 4
Bestimme den Grad folgender Potenzfunktionen, mache eine Aussage über das Symmetrieverhalten, den Verlauf des Graphen und die Wertemenge. Zeichne die Graphen jeweils in ein Koordinatensystem.
- 5
Der Graph der Potenzfunktion vierten Grades soll um 3 Einheiten nach rechts verschoben und anschließend um den Faktor 2 gestreckt werden.
a. Gib die Funktionsgleichung für den verschobenen Graphen an.
b. Weise nach, dass der Graph weder zur y-Achse noch zum Ursprung symmetrisch ist.
- 6
Gib jeweils den Definitionsbereich für die Wurzelfunktion an.
- 7
Gegeben sind die beiden Wurzelfunktionen und .
Bestimme für beide Funktionen jeweils den maximalen Definitionsbereich.
Gib für beide Funktionen jeweils die Schnittpunkte mit den Koordinatenachsen an.
Zeichne beide Graphen für in ein Koordinatensystem ein. Rechne dazu einige Funktionswerte aus.
In welchem Punkt schneiden sich die Graphen von und ?
Beide Funktionen werden um nach rechts verschoben und mit dem Faktor gestreckt. Wie heißen die neuen Funktionsgleichungen und ?
- 8
Gegeben ist die Funktion .
Bestimme den maximalen Definitionsbereich.
Zeichne mithilfe einer Wertetabelle den Graphen der Funktion für
Berechne den Schnittpunkt mit der -Achse.
Tipp: Es muss zweimal quadriert werden.
- 9
Der Marineclub hat als Logo einen stilisierten Fisch (siehe Abbildung).
Das Logo wird durch die beiden Randfunktionen und modelliert. Dabei ist die untere Randfunktion gegeben durch .
Wie lautet die Funktionsgleichung von ?
Berechne die Nullstellen von und skaliere die Koordinatenachsen in der Abbildung.
Bestimme den Definitionsbereich der Funktion .
- 10
Gegeben sind die beiden Funktionen und .
Berechne, in welchem Punkt sich die beiden Funktionsgraphen schneiden.
Zeichne die beiden Graphen mithilfe einer Wertetabelle.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?