Aufgaben zu Bernoulli-Kette und Binomialverteilung
Mit diesen gemischten Übungsaufgaben lernst du, Bernoulli-Ketten zu erkennen und Wahrscheinlichkeiten mit der Binomialverteilung zu berechnen.
- 1
In einem Forum wird eine wichtige Frage gestellt, woraufhin 6 Personen eine Antwort formulieren, ohne die Antwort der anderen gesehen zu haben. Hierbei gibt jeder von ihnen mit einer 70%igen Wahrscheinlichkeit die richtige Antwort.
Wie könnte man dies als Bernoulli-Kette darstellen?
Mit welcher Wahrscheinlichkeit
(1) haben alle sechs mit ihrer Antwort recht?
(2) hat keiner von ihnen recht?
(3) geben genau der erste und letzte die richtige Antwort?
(4) gibt mindestens einer die richtige Antwort?
Wie viele Personen müssten mindestens auf die Frage antworten, um mit einer Wahrscheinlichkeit, die größer als 99% ist, zumindest eine richtige Antwort zu erhalten?
- 2
Eine bestimmte Maschine besteht aus 8 unabhängig voneinander arbeitenden Teilen. Jedes Teil funktioniert mit der Wahrscheinlichkeit p nicht. Fallen mindestens 2 dieser Teile aus, wird die Maschine funktionsunfähig.
Wie groß darf p, auf eine Stelle hinter dem Komma gerundet, höchstens sein, damit die Maschine mit (mindestens) 80% Sicherheit arbeiten kann?
- 3
Eine Firma stellt Computertastaturen her, von denen 2 % Ausschuss sind. Bestimme die Anzahl der Tastaturen, die mindestens produziert werden müssen, damit mit 90%iger Wahrscheinlichkeit zumindest eine defekte dabei ist.
- 4
In einem Multiple-Choice-Test gibt es 20 Aufgaben, bei denen man aus drei möglichen Lösungen die richtige ankreuzen muss. Felix hat sich nicht auf den Test vorbereitet. Mit welcher Wahrscheinlichkeit wird er trotzdem genau die Hälfte der Fragen richtig beantworten?
- 5
Aus einem Kartenspiel mit 52 Karten wird immer eine Karte gezogen und dann wieder zurückgesteckt.
Wie oft muss dies wiederholt werden, um mit einer Wahrscheinlichkeit von 60% mindestens zwei Pikkarten zu ziehen?
- 6
In einer Urne befinden sich 13 weiße und 16 rote Kugeln, von denen 10 zufällig herausgegriffen werden. Wie hoch ist die Wahrscheinlichkeit, dass unter ihnen genau 6 weiße sind?
- 7
In einer Bar gibt es jeden Samstag Abend ein Würfelspiel. Hierbei kann der Barbesucher seinen bestellten Cocktail umsonst trinken, wenn er gewinnt.
Die Regeln sind einfach: Barkeeper und Kunde würfeln einen sechsseitigen, nichtgezinkten Würfel.
Würfelt der Besucher eine höhere Zahl als der Barkeeper, gewinnt er.
Wie oft muss ein Besucher würfeln, damit seine Gewinnwahrscheinlichkeit auf einen Gratis-Cocktail bei mindestens 80% liegen?
Eine Gruppe von 5 Personen trinken an einem Samstag 10 Cocktails. Wie wahrscheinlich ist es, dass
AKein Cocktail gewonnen wird?
BGenau drei Cocktails gewonnen werden?
CMehr als drei Cocktails gewonnen werden?
DGenau neun Cocktails gewonnen werden?
EAlle zehn Cocktails gewonnen werden?
Wie oft muss die Gruppe das Spiel mit dem Barkeeper spielen, damit sie zu mindestens 95% Wahrscheinlichkeit zehn Cocktails gewinnen?
Der durchschnittliche Preis für einen Cocktail beträgt 6,90€. Die Kosten für diesen inklusive dem Lohn für den Barkeeper sind für den Betreiber der Bar etwa 4€. Ein durchschnittlicher Gast trinkt 1,5 Cocktails. An einem Freitag (ohne dieses Angebot) trinken die Gäste am Abend etwa 120 Cocktails.
Wie viele Gäste mehr müssen durch das besondere Spiel angelockt werden, damit sich dieses für den Betreiber der Bar lohnt?
Ein Gast ist ein Halunke, der mogelt. Er nutzt die Unaufmerksamkeit des Kellners aus, indem er seinen Wurf zunächst unter dem Würfelbecher heimlich betrachtet und bei einer gewürfelten 1-3 den Würfel nochmal unbemerkt würfelt.
Wie ist nun seine Gewinnchance?
- 8
Eine Firma für Bohrmaschinen stellt mit Ausschuss her. Das heißt, dass jede fünfte Bohrmaschine fehlerhaft hergestellt wird.
Wie hoch ist die Wahrscheinlichkeit, dass unter 100 zufällig gewählten Bohrmaschinen kein Ausschussstück zu finden ist?
Wie hoch ist die Wahrscheinlichkeit, dass genau 20 Bohrmaschinen zum Ausschuss zählen?
- 9
Lukas ist Biathlet und besitzt eine Treffsicherheit von . Nach einem Durchgang auf seinen Langlauf-Ski legt sich Lukas an den Schießstand und gibt Schüsse auf die Scheiben.

Berechne die Wahrscheinlichkeit, dass Lukas alle Scheiben trifft.
Bestimme die Wahrscheinlichkeit, dass Lukas die ersten beiden trifft.
Nach einer weiteren Runde Langlauf, fällt es Lukas schwerer sich zu konzentrieren. Seine Treffsicherheit beträgt ab jetzt . Nach seinem Durchgang zeigen die Scheiben das folgende Muster:
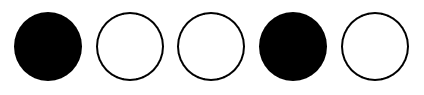
Mit welcher Wahrscheinlichkeit hat er genau dieses Muster getroffen?
Für den letzten Durchgang benötigt er genau vier Treffer. Wie viele Muster kann Lukas auf seinen Scheiben schießen, damit dieses Ereignis erfüllt ist?
Begründe, dass sich die Wahrscheinlichkeit für das Ereignis
folgendermaßen berechnen lässt:
- 10
Was ist der Unterschied zwischen einem Laplace-Experiment und einem Bernoulli-Experiment?
- 11
Was ist eine Bernoulli-Kette im Vergleich zu einem Bernoulli-Experiment?
- 12
Entscheide jeweils, ob es sich um ein Laplace-Experiment, ein Bernoulli-Experiment, beides oder keins von beidem handelt.
Ein fairer Würfel wird geworfen und die Augenzahl notiert
Ein fairer Würfel wird geworfen und notiert, ob eine 6 gefallen ist oder nicht.
Es wird morgens aus dem Fenster geschaut und notiert, welches Wetter draußen ist.
Eine zufällige Person wird nach ihrer Blutgruppe (A/B/AB/0) gefragt.
Eine faire Münze wird einmal geworfen.
Eine gezinkte Münze wird einmal geworfen.
Eine zufällig ausgewählte Person in der Bevölkerung wird gefragt, ob sie raucht.
- 13
Entscheide jeweils, ob es sich um eine Bernoulli-Kette handelt.
Aus einer Urne mit roten und blauen Kugeln wird mit Zurücklegen fünfmal hintereinander gezogen.
Aus einer Urne mit roten und blauen Kugeln werden ohne Zurücklegen fünf Kugeln nacheinander entnommen
- 14
Wofür stehen bei einer Bernoulli-Kette beziehungsweise bei einer binomialverteilten Zufallsgröße die Buchstaben und ?
- 15
Gib für jede Situation an, was und ist.
Du kannst es ins Eingabefeld in der Form eingeben.
(Beispiel für und wäre die Eingabe )
Eine faire Münze wird mal geworfen. Es soll genau mal Zahl angezeigt werden.
der Weltbevölkerung können ihre Zunge rollen. Es werden Personen befragt und sollen die Eigenschaft besitzen.
Eine gezinkte Münze zeigt in der Fälle Kopf. Sie wird mal geworfen. Es soll mal Zahl angezeigt werden.
- 16
Annäherung an die Formel der Bernoulli-Kette
Aus einer Urne mit roten und blauen Kugeln wird dreimal mit Zurücklegen gezogen. Bestimme jeweils einen Term für die Wahrscheinlichkeit der Ereignisse und und vereinfache ihn zunächst, ohne den Termwert zu berechnen.
Erkläre deine Beobachtung, in dem du das Ereignis mit Worten beschreibst und bestimme .
- 17
Die Wahrscheinlichkeit, bei einer Bernoulli-Kette mit Länge und einer Trefferwahrscheinlichkeit genau Treffer zu erzielen, kann bestimmt werden durch:
Erkläre die Bedeutung jedes Faktors im Produkt
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
