Aufgaben zur Kurvendiskussion - lernen mit Serlo!

Es ist die Funktion $f (x) = x^{3} - 3 x - 2$ gegeben.

Bestimme Nullstellen, Extrempunkte und Wendepunkte von $G_{f}$ . Zeichne $G_{f}$ .

Nullstellenbestimmung
Bestimme zuerst die Nullstellen von $f (x) = x^{3} - 3 x - 2$ , indem du die Funktion gleich 0 setzt:
$0 = x^{3} - 3 x - 2$
Die erste Nullstelle muss erraten werden. Durch ausprobieren ermittelt man beispielsweise $x_{1} = - 1$
Mit Polynomdivision wird jetzt eine neue Gleichung aufgestellt.
$\begin{array}{l} (x^{3} - 3 x - 2) : (x + 1) = x^{2} - x - 2 \\ - (x^{3} + x^{2}) \\ - x^{2} - 3 x \\ - (- x^{2} - x) \\ - 2 x - 2 \\ - (- 2 x - 2) \\ 0 \end{array}$
Die berechnete Funktion wird gleich 0 gesetzt um die beiden anderen Nullstellen zu ermitteln.
$0$ $=$ $x^{2} - x - 2$
↓
Löse beispielsweise mit der Mitternachtsformel.
$x_{2,3}$ $=$ $\frac{1 \pm \sqrt{{(- 1)}^{2} - 4 \cdot 1 \cdot (- 2)}}{2 \cdot 1}$
$=$ $\frac{1 \pm \sqrt{1 - (- 8)}}{2}$
$=$ $\frac{1 \pm \sqrt{9}}{2}$
$=$ $\frac{1 \pm 3}{2}$
$x_{2} = \frac{4}{2} = 2; x_{3} = \frac{- 2}{2} = - 1$
Die Funktion hat demnach eine einfache Nullstelle bei $x_{2} = 2$ und eine doppelte Nullstelle bei $x_{1,3} = - 1$ .
Ableiten
Leite die Funktion zweimal ab.
$f (x) = x^{3} - 3 x - 2$
$f^{'} (x) = 3 x^{2} - 3$
$f^{''} (x) = 6 x$
Extrema bestimmen
Setze die erste Ableitung gleich $0$ .
$0$ $=$ $f^{'} (x)$
$0$ $=$ $3 x^{2} - 3$ $+ 3$
$3$ $=$ $3 x^{2}$ $: 3$
$1$ $=$ $x^{2}$
$x_{1} = 1; x_{2} = - 1$
Extremum bei $x_{1} = 1$ :
Setze $x_{1}$ in $f (x) = x^{3} - 3 x - 2$ ein.
$f (1) = 1^{3} - 3 \cdot 1 - 2 = - 4$
Setze $x_{1}$ in $f^{''} (x) = 6 x$ ein:
$f^{''} (x) = 6 \cdot 1 = 6$
Da $f^{''} (1) > 0$ hat $f (x)$ in $T P (1 | - 4)$ einen Tiefpunkt.
Extremum bei $x_{2} = - 1$ :
Setze $x_{2}$ in $f (x) = x^{3} - 3 x - 2$ ein.
$f (- 1) = {(- 1)}^{3} - 3 \cdot (- 1) - 2 = - 1 + 3 - 2 = 0$
Setze $x_{2}$ in $f^{''} (x) = 6 x$ ein:
$f^{''} (x) = 6 \cdot (- 1) = - 6$
Da $f^{''} (- 1) < 0$ hat $f (x)$ in $H P (- 1 | 0)$ einen Hochpunkt.
Wendepunkte bestimmen
Bestimme nun noch die Wendepunkte. Setze dazu $f^{''} (x) = 6 x$ gleich 0.
$f^{''} (x)$ $=$ $0$
$6 x$ $=$ $0$ $: 6$
$x$ $=$ $0$
Setze $x = 0$ in $f (x) = x^{3} - 3 x - 2$ ein:
$f (0) = 0^{3} - 3 \cdot 0 - 2 = - 2$
Da $f^{'''} (x) = 6 \neq 0$ ist, gibt es einen Wendepunkt:
Der Wendepunkt lautet $W P (0 | - 2)$ .
Graph der Funktion
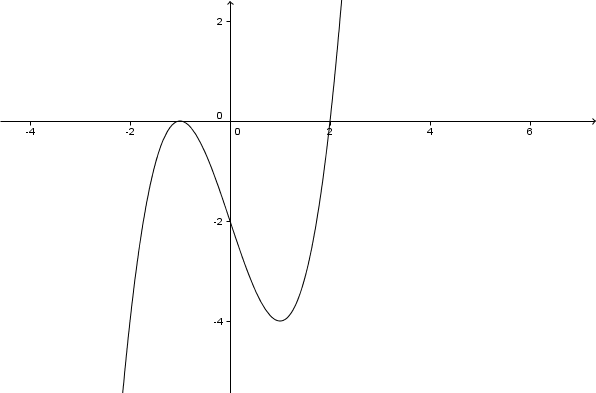
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne die Gleichungen der Tangente $t$ und Normale $n$ im Wendepunkt.

Tangente aufstellen
Stelle die Tangente im Wendepunkt $W P (0 | - 2)$ auf.
Setze den x-Wert des Wendepunkts, also $0$ , in $f^{'} (x) = 3 x^{2} - 3$ ein:
$f^{'} (0) = 3 \cdot 0^{2} - 3 = - 3$
$- 3$ ist die Steigung $m$ der Tangente. Setze das bestimmte m und die Koordinaten des Wendepunkts in die allgemeine Geradengleichung $y = m x + t$ ein, um $t$ zu bestimmen.
$y$ $=$ $m x + t$
↓
$m = - 3$ einsetzen
$y$ $=$ $- 3 x + t$
↓
Setze $W P (0 | - 2)$ in die Gleichung ein. $\Rightarrow x = 0$ und $y = - 2$ .
$- 2$ $=$ $- 3 \cdot 0 + t$
$- 2$ $=$ $t$
Mit $t$ und $m$ kannst du die Gleichung der Tangente aufstellen.
Die Gleichung der Tangente lautet t: $y = - 3 x - 2$
Normale aufstellen
Stelle die Normalengleichung $n$ auf. Für die Steigung der Normalen $m_{n}$ und die Steigung der Tangenten $m_{t} = - 3$ gilt:
$m_{t} \cdot m_{n}$ $=$ $- 1$
↓
$m_{t} = - 3$
$- 3 \cdot m_{n}$ $=$ $- 1$ $: (- 3)$
$m_{n}$ $=$ $\frac{1}{3}$
Das bestimmte $m_{n}$ und die Koordinaten des Wendepunkts kannst du in die allgemeinen Geradengleichung einsetzen, um $t$ zu bestimmen.
$y$ $=$ $m_{n} \cdot x + t$
↓
$m_{n} = \frac{1}{3}$ einsetzen.
$y$ $=$ $\frac{1}{3} x + t$
↓
Setze $W P (0 | - 2)$ in die Gleichung ein. $\Rightarrow x = 0$ und $y = - 2$ .
$- 2$ $=$ $\frac{1}{3} \cdot 0 + t$
$- 2$ $=$ $t$
Mit $t$ und $m_{n}$ kannst du die Gleichung der Tangente aufstellen.
Die Gleichung der Normale lautet $n$ : $y = \frac{1}{3} x - 2$
Graph der Funktion mit Normale und Tangente
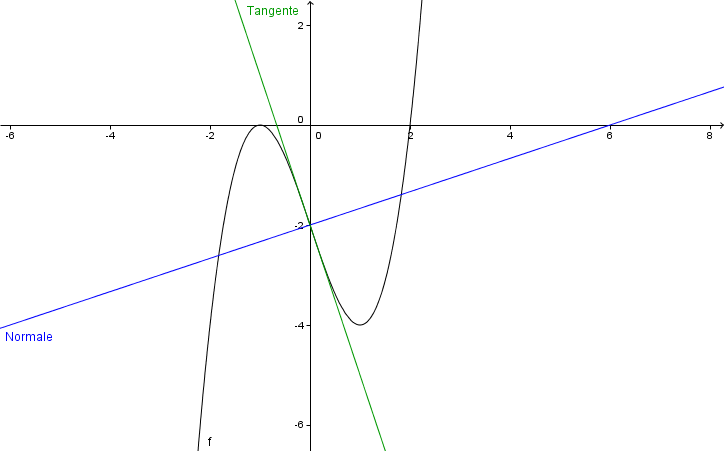
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne den Inhalt der beiden Flächenstücke, die von $G_{f}$ und der Normalen $n$ begrenzt sind.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Zur Bestimmung des Integrals werden die Schnittpunkte der beiden Funktionen benötigt.
Schnittstelle der Funktionen berechnen
Setze beide Funktionen gleich.
$y = \frac{1}{3} x - 2$
$f (x) = x^{3} - 3 x - 2$
$y$ $=$ $f (x)$
$\frac{1}{3} x - 2$ $=$ $x^{3} - 3 x - 2$ $- \frac{1}{3} x + 2$
$0$ $=$ $x^{3} - \frac{10}{3} x$
↓
$x$ ausklammern.
$0$ $=$ $x \cdot (x^{2} - \frac{10}{3})$
Die erste Nullstelle ist $x_{1} = 0$ . Um die weiteren Nullstellen zu bestimmen, muss die Klammer $(x^{2} - \frac{10}{3}) = 0$ berechnet werden.
$0$ $=$ $x^{2} - \frac{10}{3}$ $+ \frac{10}{3}$
$\frac{10}{3}$ $=$ $x^{2}$
$x_{2,3}$ $=$ $\pm \sqrt{\frac{10}{3}}$
Integral aufstellen
Es gibt zwei Flächen die durch die Schnitte entstehen.
$A = | \int_{- \sqrt{\frac{10}{3}}}^{0} ((x^{3} - 3 x - 2) - (\frac{1}{3} x - 2)) dx | + | \int_{0}^{\sqrt{\frac{10}{3}}} ((x^{3} - 3 x - 2) - (\frac{1}{3} x - 2)) dx |$
Vereinfache zuerst den Integranden:
$(x^{3} - 3 x - 2) - (\frac{1}{3} x - 2)$ $=$ $x^{3} - 3 x - 2 - \frac{1}{3} x + 2$
$=$ $x^{3} - \frac{10}{3} x$
Integriere $\int_{- \sqrt{\frac{10}{3}}}^{0} (x^{3} - \frac{10}{3} x) d x$ und dann $\int_{0}^{\sqrt{\frac{10}{3}}} (x^{3} - \frac{10}{3} x) d x$
$\int_{- \sqrt{\frac{10}{3}}}^{0} (x^{3} - \frac{10}{3} x) d x$ $=$ ${[\frac{1}{4} x^{4} - \frac{10}{3 \cdot 2} x^{2}]}_{- \sqrt{\frac{10}{3}}}^{0}$
$=$ $(\frac{1}{4} \cdot 0^{4} - \frac{5}{3} \cdot 0^{2}) - (\frac{1}{4} {(- \sqrt{\frac{10}{3}})}^{4} - \frac{5}{3} {(- \sqrt{\frac{10}{3}})}^{2})$
$=$ $- (\frac{1}{4} \cdot {(\frac{10}{3})}^{2} - \frac{5}{3} \cdot \frac{10}{3})$
$=$ $- (\frac{25}{9} - \frac{50}{9})$
$=$ $\frac{25}{9}$
$\int_{0}^{\sqrt{\frac{10}{3}}} (x^{3} - \frac{10}{3} x) d x$ $=$ ${[\frac{1}{4} x^{4} - \frac{10}{3 \cdot 2} x^{2}]}_{0}^{\sqrt{\frac{10}{3}}}$
$=$ $(\frac{1}{4} {\sqrt{\frac{10}{3}}}^{4} - \frac{5}{3} {\sqrt{\frac{10}{3}}}^{2}) - (\frac{1}{4} \cdot 0^{4} - \frac{5}{3} \cdot 0^{2})$
$=$ $(\frac{1}{4} \cdot {(\frac{10}{3})}^{2} - \frac{5}{3} \cdot \frac{10}{3})$
$=$ $\frac{25}{9} - \frac{50}{9}$
$=$ $- \frac{25}{9}$
$A = | \int_{- \sqrt{\frac{10}{3}}}^{0} ((x^{3} - 3 x - 2) - (\frac{1}{3} x - 2)) dx | + | \int_{0}^{\sqrt{\frac{10}{3}}} ((x^{3} - 3 x - 2) - (\frac{1}{3} x - 2)) dx | = | \frac{25}{9} | + | - \frac{25}{9} | = \frac{25}{9} + \frac{25}{9} = \frac{50}{9}$
Die gesuchte Fläche hat den Flächeninhalt $ \frac{50}{9} \approx 5,56950 \approx 5,57$ Flächeneinheiten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$0$	$=$	$x^{2} - x - 2$
	↓	Löse beispielsweise mit der Mitternachtsformel.
$x_{2,3}$	$=$	$\frac{1 \pm \sqrt{{(- 1)}^{2} - 4 \cdot 1 \cdot (- 2)}}{2 \cdot 1}$
	$=$	$\frac{1 \pm \sqrt{1 - (- 8)}}{2}$
	$=$	$\frac{1 \pm \sqrt{9}}{2}$
	$=$	$\frac{1 \pm 3}{2}$

$0$	$=$	$f^{'} (x)$
$0$	$=$	$3 x^{2} - 3$	$+ 3$
$3$	$=$	$3 x^{2}$	$: 3$
$1$	$=$	$x^{2}$

$y$	$=$	$m x + t$
	↓	$m = - 3$ einsetzen
$y$	$=$	$- 3 x + t$
	↓	Setze $W P (0 \| - 2)$ in die Gleichung ein. $\Rightarrow x = 0$ und $y = - 2$ .
$- 2$	$=$	$- 3 \cdot 0 + t$
$- 2$	$=$	$t$

$m_{t} \cdot m_{n}$	$=$	$- 1$
	↓	$m_{t} = - 3$
$- 3 \cdot m_{n}$	$=$	$- 1$	$: (- 3)$
$m_{n}$	$=$	$\frac{1}{3}$

$y$	$=$	$m_{n} \cdot x + t$
	↓	$m_{n} = \frac{1}{3}$ einsetzen.
$y$	$=$	$\frac{1}{3} x + t$
	↓	Setze $W P (0 \| - 2)$ in die Gleichung ein. $\Rightarrow x = 0$ und $y = - 2$ .
$- 2$	$=$	$\frac{1}{3} \cdot 0 + t$
$- 2$	$=$	$t$

$y$	$=$	$f (x)$
$\frac{1}{3} x - 2$	$=$	$x^{3} - 3 x - 2$	$- \frac{1}{3} x + 2$
$0$	$=$	$x^{3} - \frac{10}{3} x$
	↓	$x$ ausklammern.
$0$	$=$	$x \cdot (x^{2} - \frac{10}{3})$

$0$	$=$	$x^{2} - \frac{10}{3}$	$+ \frac{10}{3}$
$\frac{10}{3}$	$=$	$x^{2}$
$x_{2,3}$	$=$	$\pm \sqrt{\frac{10}{3}}$

$(x^{3} - 3 x - 2) - (\frac{1}{3} x - 2)$	$=$	$x^{3} - 3 x - 2 - \frac{1}{3} x + 2$
	$=$	$x^{3} - \frac{10}{3} x$

$\int_{- \sqrt{\frac{10}{3}}}^{0} (x^{3} - \frac{10}{3} x) d x$	$=$	${[\frac{1}{4} x^{4} - \frac{10}{3 \cdot 2} x^{2}]}_{- \sqrt{\frac{10}{3}}}^{0}$
	$=$	$(\frac{1}{4} \cdot 0^{4} - \frac{5}{3} \cdot 0^{2}) - (\frac{1}{4} {(- \sqrt{\frac{10}{3}})}^{4} - \frac{5}{3} {(- \sqrt{\frac{10}{3}})}^{2})$
	$=$	$- (\frac{1}{4} \cdot {(\frac{10}{3})}^{2} - \frac{5}{3} \cdot \frac{10}{3})$
	$=$	$- (\frac{25}{9} - \frac{50}{9})$
	$=$	$\frac{25}{9}$

$\int_{0}^{\sqrt{\frac{10}{3}}} (x^{3} - \frac{10}{3} x) d x$	$=$	${[\frac{1}{4} x^{4} - \frac{10}{3 \cdot 2} x^{2}]}_{0}^{\sqrt{\frac{10}{3}}}$
	$=$	$(\frac{1}{4} {\sqrt{\frac{10}{3}}}^{4} - \frac{5}{3} {\sqrt{\frac{10}{3}}}^{2}) - (\frac{1}{4} \cdot 0^{4} - \frac{5}{3} \cdot 0^{2})$
	$=$	$(\frac{1}{4} \cdot {(\frac{10}{3})}^{2} - \frac{5}{3} \cdot \frac{10}{3})$
	$=$	$\frac{25}{9} - \frac{50}{9}$
	$=$	$- \frac{25}{9}$

Nullstellenbestimmung

Ableiten

Extrema bestimmen

Extremum bei x1=1:

Extremum bei x2=−1:

Wendepunkte bestimmen

Graph der Funktion

Hast du eine Frage oder Feedback?

Tangente aufstellen

Normale aufstellen

Graph der Funktion mit Normale und Tangente

Hast du eine Frage oder Feedback?

Schnittstelle der Funktionen berechnen

Integral aufstellen

Hast du eine Frage oder Feedback?

Extremum bei $x_{1} = 1$ :

Extremum bei $x_{2} = - 1$ :