Aufgaben zur Diskussion von e-Funktionen

Diskutiere folgende Funktionen so weit, bis du den Graphen zeichnen kannst. Gib gegebenenfalls die Asymptoten an:

$f (x) = e \cdot e^{x}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Definitionsbereich festlegen
Da die Funktion keine Brüche, Wurzeln oder andere Dinge enthält, die den Definitionsbereich einschränken könnten, ist der Definitionsbereich der Funktion $D_{f} = ℝ$ .
Nullstellenbestimmung
Die $e$ -Funktion besitzt keine Nullstelle, weshalb die betrachtete Funktion $f$ ebenfalls keine besitzt.
Ableitungen
1. Ableitung
$f (x) = e \cdot e^{x}$
Die Ableitung von $e^{x}$ ist wiederum $e^{x}$ . Der Faktor $e$ bleibt bestehen.
$f^{'} (x) = e \cdot e^{x}$
2. Ableitung
$f^{'} (x) = e \cdot e^{x}$
Selber Vorgang wie bei der ersten Ableitung.
$f^{''} (x) = e \cdot e^{x}$
Extrema bestimmen
Da $f^{'} (x) = e \cdot e^{x}$ nie Null wird, hat die Funktion keine Extrema.
Wendepunkte bestimmen
Da $f^{''} (x) = e \cdot e^{x}$ nie Null wird, hat die Funktion keine Wendepunkte.
Grenzwertbetrachtung
$D_{f} = ℝ$
Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm \infty$ betrachtet werden.
gegen $+ \infty$
$\lim_{x \to \infty} \underset{\to \infty}{\underset{⏟}{e \cdot e^{x}}} = \infty$
gegen $- \infty$
$\lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{e \cdot e^{x}}} = 0^{+}$
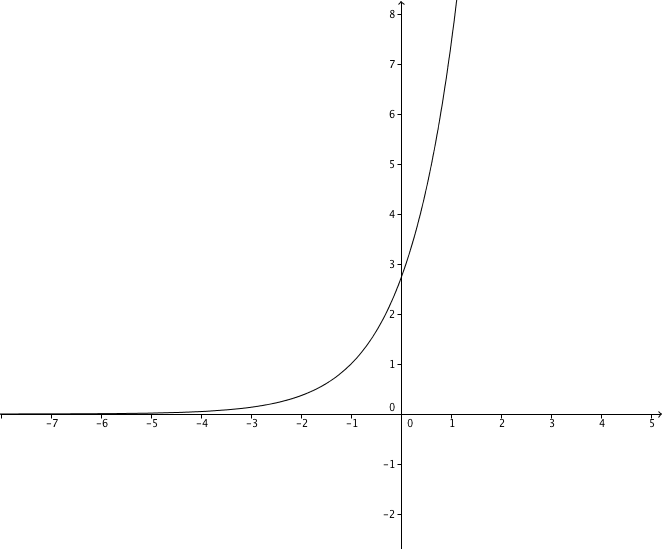
Damit besitzt $f$ eine horizontale Asymptote bei 0 für die Annäherung an $- \infty$ .
Symmetrieverhalten
$f (x) = e \cdot e^{x}$
Ersetze $x$ durch $- x$ .
$f (- x) = e \cdot e^{- x}$
Da $f (- x)$ weder $- f (x)$ noch $f (x)$ ist, weist die Funktion keine Symmetrie auf.
Monotonieverhalten
Um die Monotonie zu ermitteln, betrachte das Vorzeichen von $f^{'} (x)$ . Da $f^{'} (x)$ keine Nullstellen aufweist, ändert sich die Steigung von $f (x)$ auch nicht.
$f^{'} (x) = e \cdot e^{x}$
Der erste Faktor $e$ ist eine Konstante und ist positiv, der zweite Faktor $e^{x}$ ist in $D_{f} = ℝ$ immer positiv, wodurch $f^{'} (x)$ stets positiv ist.
Damit ist die Funktion streng monoton steigend in $D_{f} = ℝ$ .
Graph
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

1. Ableitung

2. Ableitung

Grenzwertbetrachtung

gegen +∞

gegen −∞

Hast du eine Frage oder Feedback?

gegen $+ \infty$

gegen $- \infty$