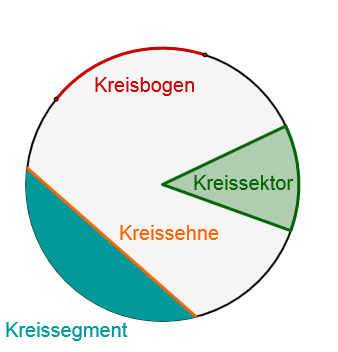
Aufgaben zur Berechnung von Kreisringen und Kreissektoren

1
Wähle die richtige Antwort aus.
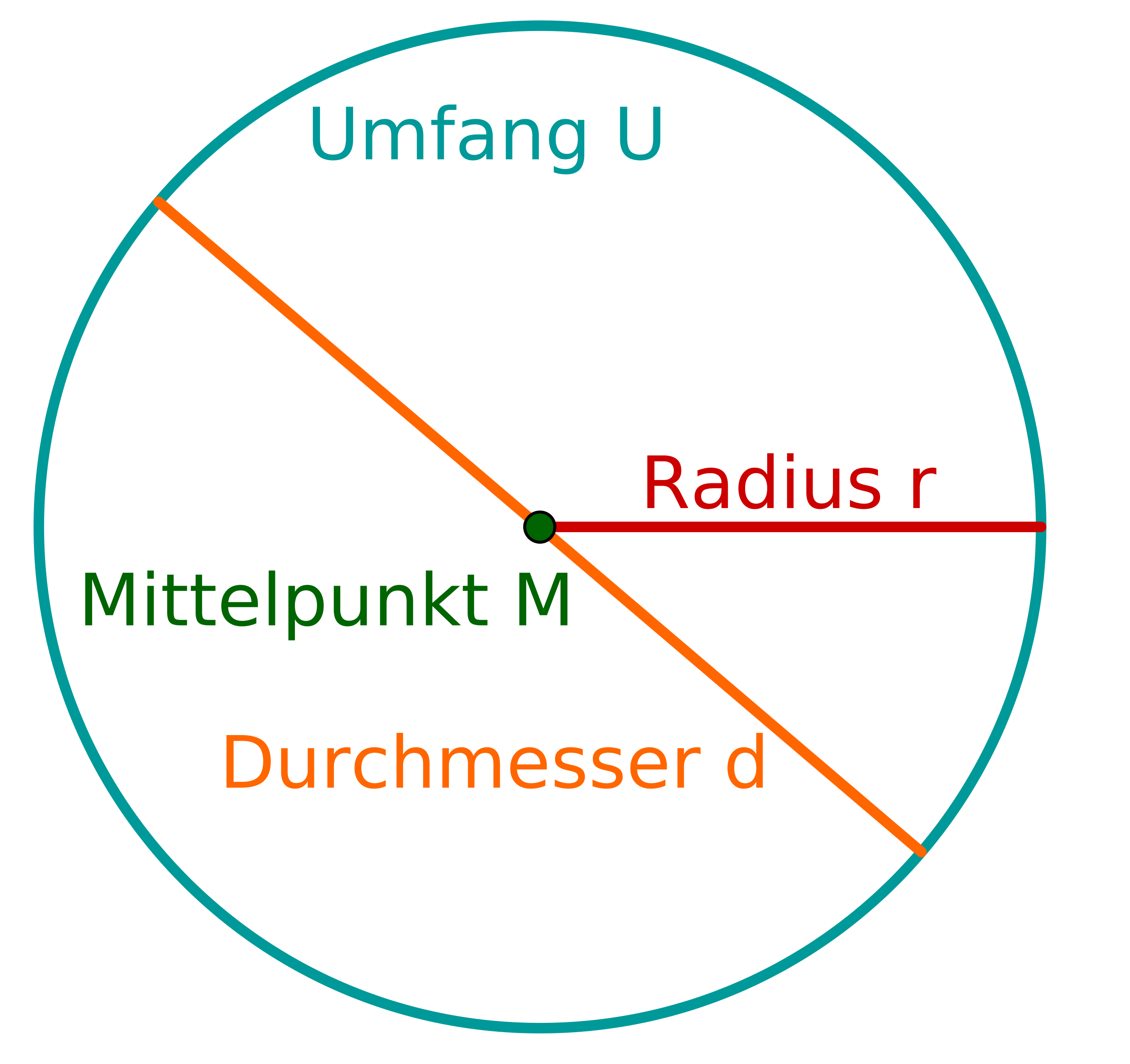
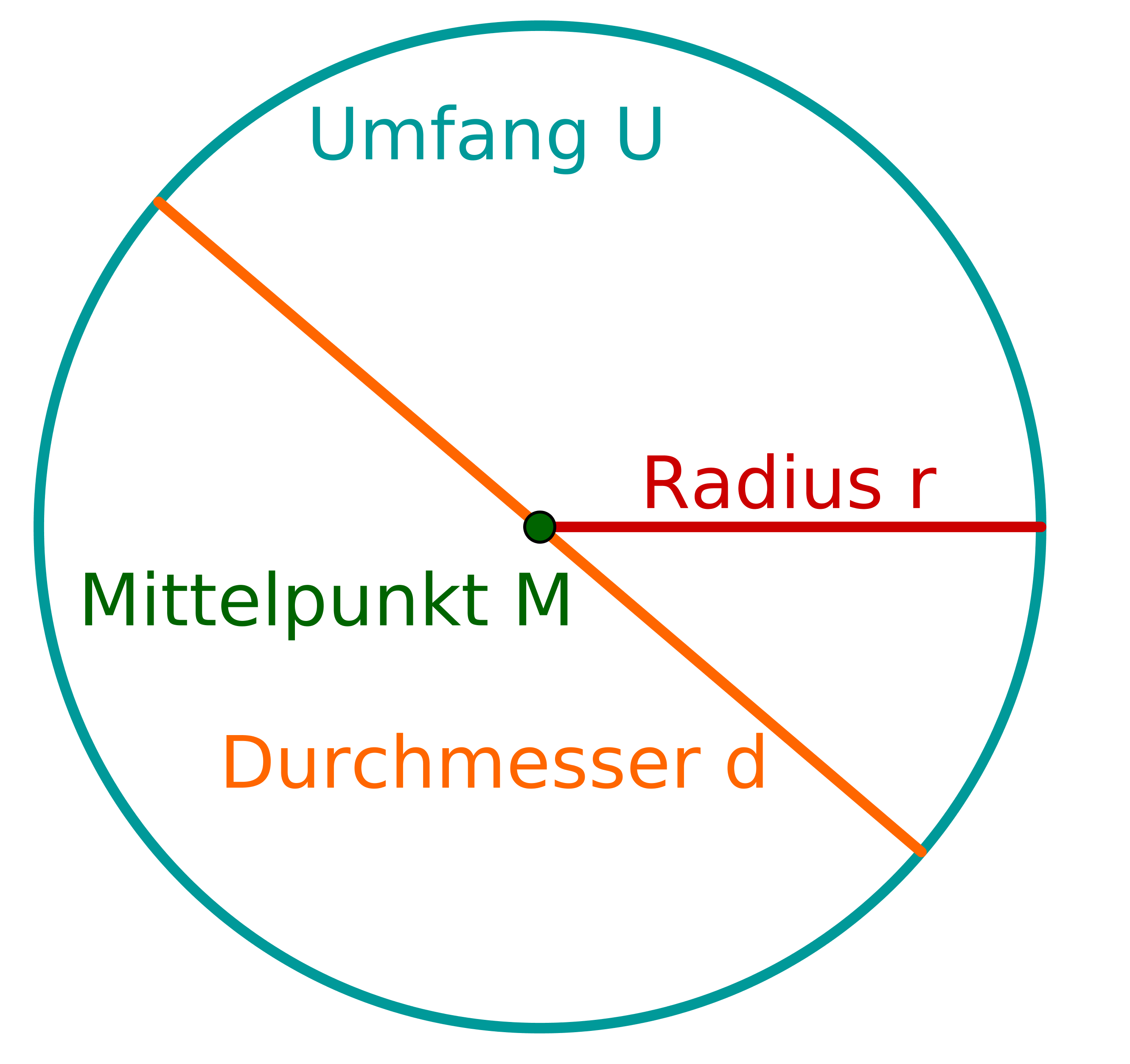
1. In welchem Bild ist der Radius rot markiert?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Radius
  Der Radius ist die Länge einer Strecke vom Mittelpunkt $M$ bis zum Rand des Kreises.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Informiere dich genau über die Begriffe: Umfang, Durchmesser, Radius.
  Sobald du die Definitionen kennst, weißt du die Antwort.
2. Wie berechnet man den Flächeninhalt $A$ von einem Kreis mit Radius $r$ ?
  $A=\pi \cdot r^2$
  $A=\pi^2 \cdot r$
  $A=\dfrac{r}{2}\cdot \pi$
  $A = 2\cdot \pi \cdot r$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Radius
  Die richtige Antwort ist $A=\pi \cdot r^2$ . Sie ist die einzige Formel unter den Antwortmöglichkeiten, bei der du eine Fläche als Ergebnis erhältst. Rechne zum Beispiel mit $r=1\text{ cm}$ . Dann erhältst du $A=\pi \cdot 1 \text{ cm}^2 \approx 3{,}14 \text{ cm}^2$ . In den anderen Formeln kommt der Radius $r$ ohne Quadrat vor und dein Ergebnis wird keine Fläche.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Denke zuerst logisch nach, welche Formel am sinnvollsten für dich erscheint. Wenn du dir nicht weiter helfen kannst, benutze deine Formelsammlung! Wenn du keine hast, recherchiere im Internet.
3. Welche Formel stimmt? (Mit $A$ ist der Flächeninhalt vom Kreis gemeint.)
  $A =\dfrac{U\cdot r}{2}$
  $A=\dfrac{\pi}{r}$
  $r=2 \cdot d$
  $U=\pi \cdot r$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Formeln zum Kreis
  Die richtige Antwort ist $A=\dfrac{U\cdot r}{2}$ .
  Um zu überprüfen, dass die Antwort stimmt, kannst du die Formel für den Umfang $U=2 \cdot \pi \cdot r$ einsetzen.
  $A=\dfrac{U\cdot r}{2} =\dfrac{2 \cdot \pi \cdot r \cdot r}{2}$
  Kürze den Bruch.
  $A=\pi \cdot r \cdot r = \pi \cdot r^2$
  Das ist die richtige Formel für den Flächeninhalt. Es wurden nur Äquivalenzumformungen verwendet. Deshalb ist auch die Ausgangsformel $A=\frac{U \cdot r}{2}$ richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Denke zuerst logisch nach, welche Formel am sinnvollsten für dich erscheint. Wenn du dir nicht weiter helfen kannst, benutze deine Formelsammlung! Wenn du keine hast, recherchiere im Internet.
4. Auf welchem Bild ist ein Kreissegment dargestellt?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis
  
  Ein Kreissegment ist im nebenstehenden Bild zu sehen.
  Die Grundbegriffe zum Kreis musst du auswendig können.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Benutze deine Formelsammlung! Wenn du keine hast, recherchiere im Internet.
2
Bestimme den Flächeninhalt der folgenden Kreissektoren. Gib deine Lösungen auf zwei Stellen nach dem Komma gerundet ein.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Formel für die Berechnung der Kreissektorfläche
  Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen. Rechne anschließend den Term aus:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
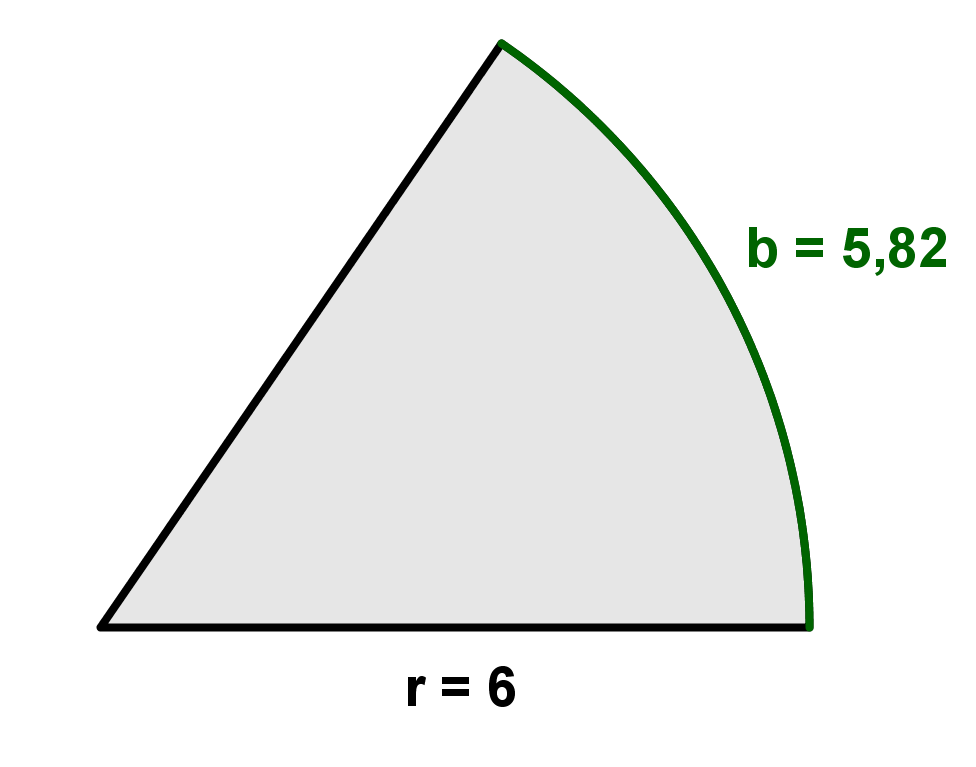
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Kreissektors
  Setze die Bogenlänge und den Radius in die Formel ein, um den Flächeninhalt zu bestimmen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
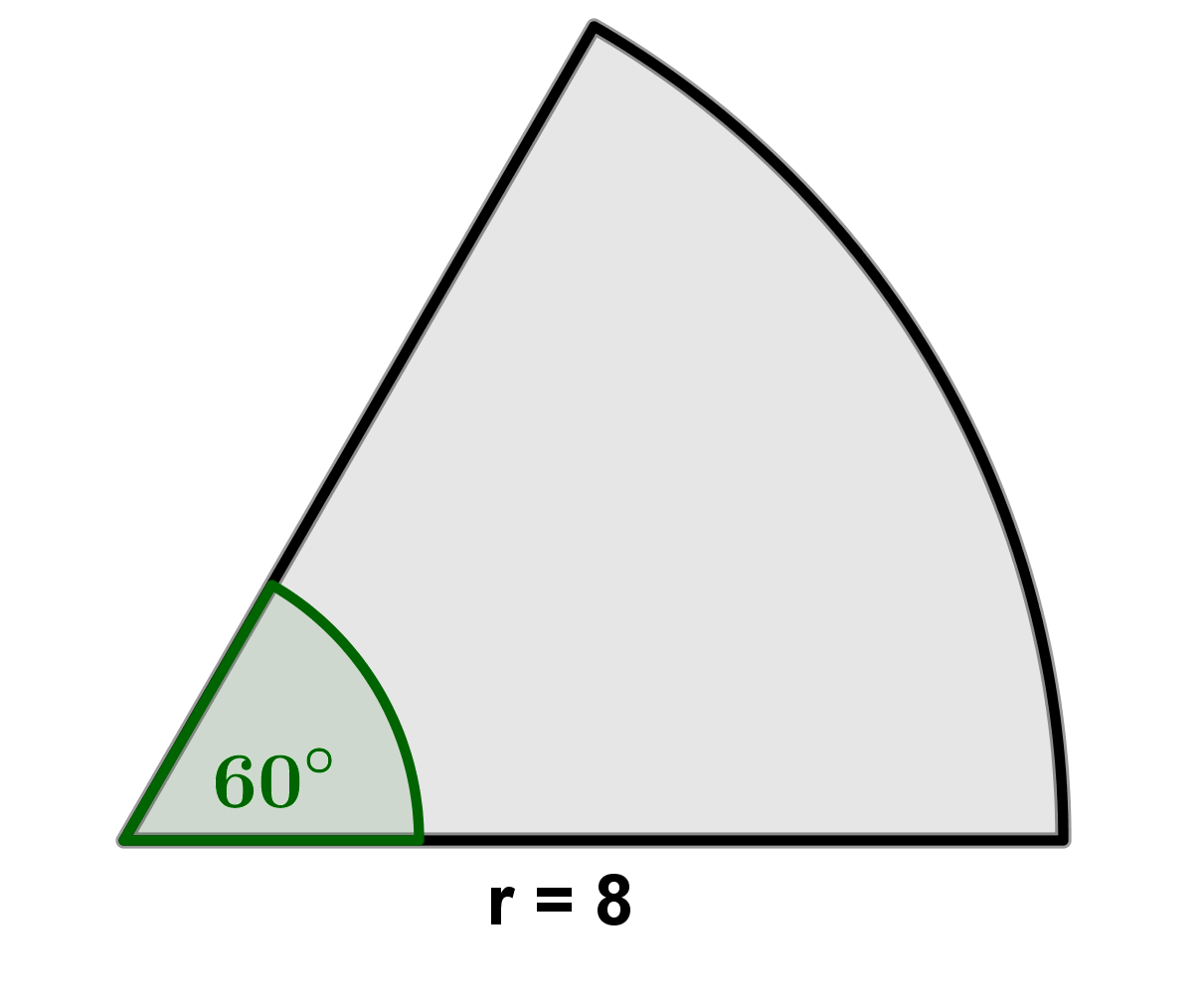
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Kreissektors
  Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen.
  Rechne aus und runde auf zwei Stellen nach dem Komma.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
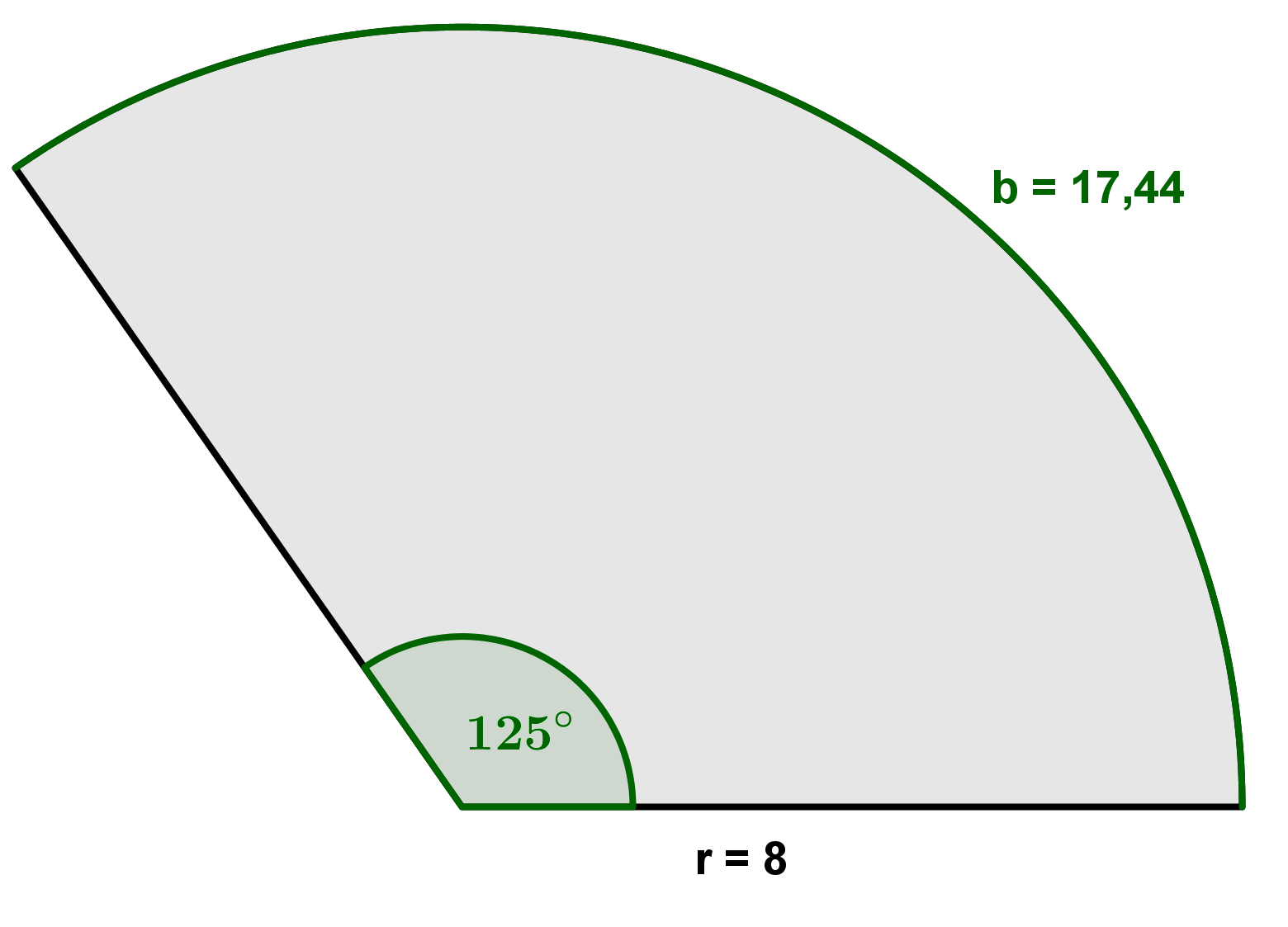
4. Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Kreissektors
  1. Möglichkeit: Mit dem Radius und dem Mittelpunktswinkel
  Benutze die Formel, in der $\alpha$ und $r$ vorkommen:
  Setze den Radius und den Mittelpunktswinkel in die Formel ein, um den Flächeninhalt zu bestimmen.
  Berechne.
  2. Möglichkeit: Mit dem Radius und der Länge des Kreisbogens
  Benutze die Formel, in der $b$ und $r$ vorkommen:
  Setze die Bogenlänge und den Radius in die Formel ein, um den Flächeninhalt zu bestimmen.
  Die kleine Abweichung zum vorherigen Ergebnis kommt vom Runden der Länge des Kreisbogens.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Der abgebildete Rasensprenger schwenkt um 40° und besprüht so eine Rasenfläche von $20\:m^2$ .
Wie groß ist seine Reichweite?
Gib das Ergebnis auf zwei Stellen nach dem Komma gerundet ein.
Quelle: Sebastian & Kari, CC BY-SA 2.0, Wikimedia Commons
m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreissektor
Bei dieser Aufgabe musst du den Radius eines Kreissektors berechnen.
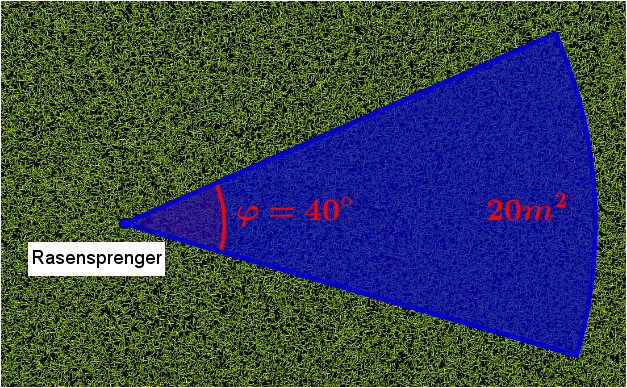
Die besprühte Rasenfläche bildet einen Kreissektor mit dem Mittelpunktswinkel $\varphi=40^\circ$ und dem gesuchten Radius r.
$\dfrac{r^2\cdot\mathrm\pi\cdot\mathrm\varphi}{360^\circ}=20\;m^2$
Setze den Wert $\varphi = 40^\circ$ in die Formel ein.
$\dfrac{r^2\cdot\mathrm\pi\cdot\mathrm40^\circ}{360^\circ}=20\;m^2$
Kürze die Winkel
$\dfrac{r^2\cdot\mathrm\pi}{9}=20\;m^2$
Löse die Gleichung nach r auf.
$r=\sqrt{\dfrac{180\;m^2}{\pi}} = \sqrt{\dfrac{180}{\pi}}m \approx 7{,}57\ m$
Der Rasensprenger reicht also $7{,}57\,\text{m}$ weit.
4
Berechne den Umfang der abgebildeten Figuren.
Beachte bei der Eingabe der Ergebnisse ins entsprechende Eingabefeld auf Folgendes:
Gib die Ergebnisse auf eine Stelle nach dem Komma gerundet und ohne Einheit ein.
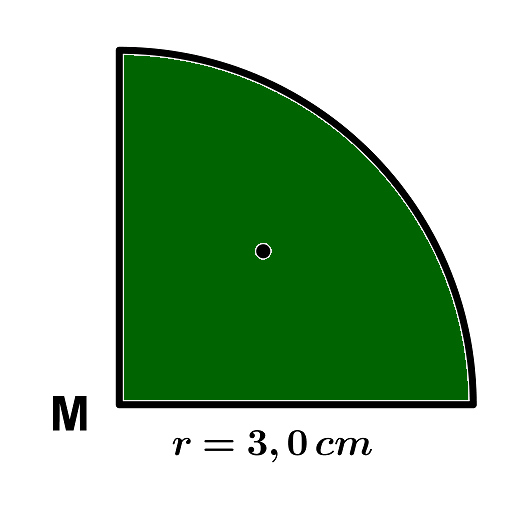
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang
  Umfang des Kreises: $U\;=\;2\cdot\pi\cdot r$
  Bei der Figur handelt es sich um einen rechtwinkligen Kreisausschnitt, also einen Kreisausschnitt mit $90^\circ$ .
  Du kannst demnach diese Gleichung durch 4 teilen bzw. mal ein Viertel nehmen, um den Umfang des Kreisbogens $U_{Kreisbogen}$ zu bestimmen.
  $U_{Kreisbogen}\;=\;\frac14\cdot2\cdot\pi\cdot r$
  Alternativ
  $U_{Kreisbogen}\;=\;2\cdot\pi\cdot r \cdot \dfrac{90^\circ}{360^\circ}= \dfrac14\cdot2\cdot\pi\cdot r$
  Alternativ kannst du aber auch gleich die Formel für die Kreisbogenlänge mit dem Winkel $\varphi = 90^\circ$ verwenden.
  Jetzt fehlen noch die 2 geraden Stücke. Diese haben gerade jeweils die Länge des Radius $r$ des Kreises. Also musst du noch zwei Mal den Radius des Kreises addieren, um den gesamten Umfang der Figur $U_{Figur}$ zu bekommen.
  $U_{Figur}\;=\;\frac14\cdot2\cdot\pi\cdot r\;+\;2\cdot r$
  Jetzt muss nur noch für $r = 3 \, cm$ eingesetzt werden.
  $U_{Figur}\;=\;\frac14\cdot2\cdot\pi\cdot3\;+\;2\cdot3$
  $U_{Figur}\;\approx\;10{,}7\,$
  Das Ergebnis ist gerundet.
  Der Umfang beträgt $10{,}7 \, cm$ ..
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
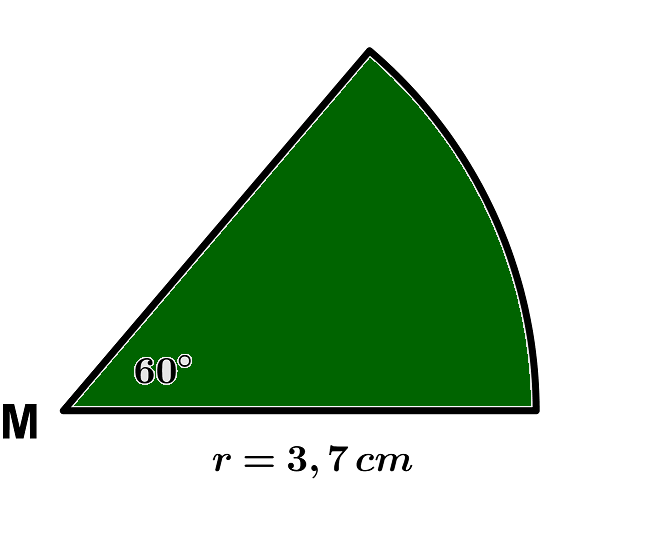
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang
  Der Umfang der Figur $U_{Figur}$ besteht aus der Länge eines Kreisbogens mit dem Winkel $60^\circ$ und den 2 geraden Stücken.
  Diese geraden Stücke haben gerade jeweils die Länge des Radius $r$ des Kreissektors. Also musst du noch zwei Mal den Radius des Kreissektors addieren, um den gesamten Umfang der Figur zu erhalten.
  $U_{Figur}= 2\cdot3{,}7\cdot\mathrm\pi\cdot\cfrac{60^\circ}{360^\circ}+2\cdot3{,}7\approx 11{,}3$
  Der Umfang beträgt $11{,}3 \, cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
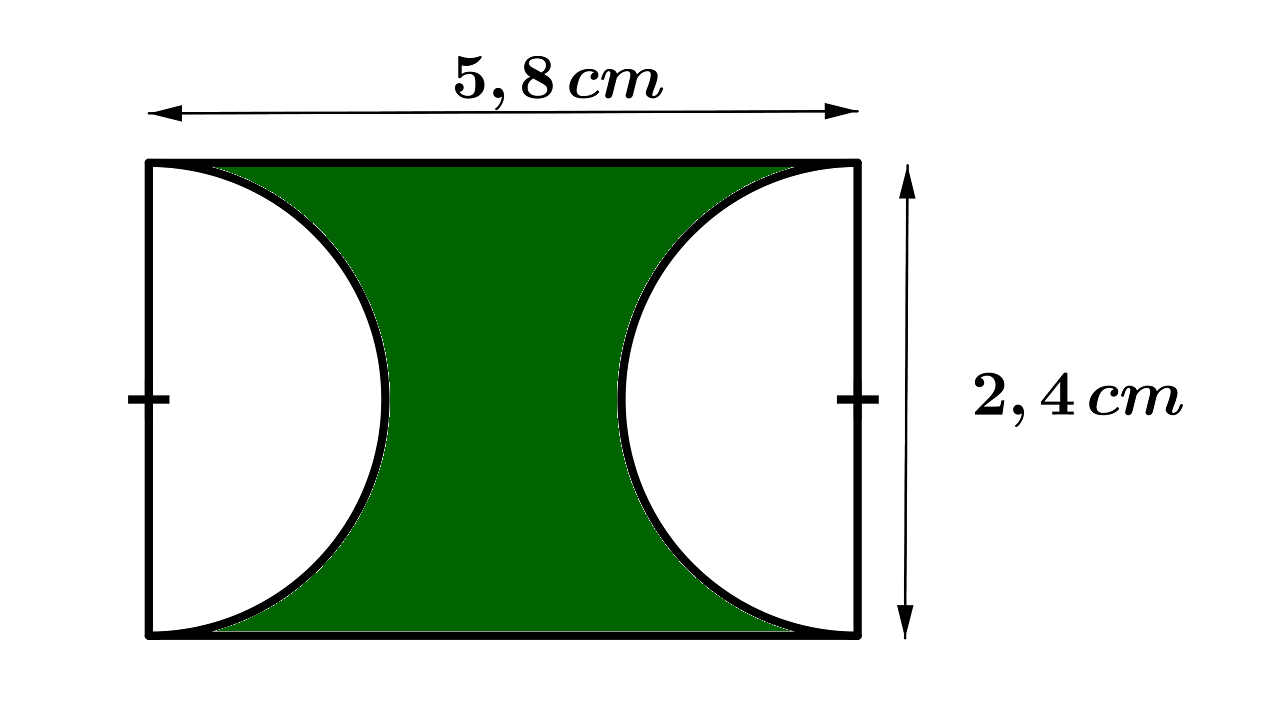
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang
  Der Umfang dieser Figur $U_{Figur}$ besteht aus zwei geraden Stücken jeweils der Länge $5{,}8\,cm$ und aus dem Umfang der zwei Halbkreise mit jeweils dem Radius $1{,}2\,cm$ .
  Wenn du die zwei Halbkreise nebeneinander legst, erkennst du, dass ein Kreis mit dem Radius $1{,}2\,cm$ entsteht.
  Du kannst folglich gleich den Umfang des Kreises ( $U_{Kreis}=2\cdot \pi \cdot r$ ) mit dem Radius $r= 1{,}2\,cm$ statt die Umfänge der zwei Halbkreise hernehmen.
  $U_{gerade \, Stücke} = 2 \cdot 5{,}8$
  $U_{Halbkreise}=U_{Kreis}= 2 \cdot \pi \cdot 1{,}2$
  Ingesamt erhält man
  $U_{Figur}=2\cdot5{,}8+2\cdot \pi \cdot 1{,}2\approx19{,}1%$
  Der Umfang beträgt $19{,}1 \, cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

In einem Kreis mit Radius $r=5\mathrm{\cm}$ ist ein Sektor mit Mittelpunktswinkel $\varphi=45^\circ$ eingezeichnet.

Gib die Fläche des Sektors und die Länge des zugehörigen Bogens an.

Berechne bei den einzelnen Figuren jeweils den Umfang und den Flächeninhalt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis

Berechnung des Umfangs

Der Umfang der Figur $U_F$ setzt sich aus zwei geraden $6 \mathrm{cm}$ langen Strecken und einem Viertel Kreisumfang zusammen.

Die Formel für den Kreisumfang lautet: $U=2\pi r$

Ein Viertel des Kreisumfangs kann dann mit $U_{\frac{1}{4}}=\frac{1}{4}\cdot(2\pi r)=0{,}5\pi r$ berechnet werden. Der Kreisradius $r$ beträgt bei dieser Figur $6 \mathrm{cm}$ , so

dass du für $U_{\frac{1}{4}}$ folgenden Wert erhältst:

$\displaystyle U_{\frac{1}{4}}$	$=$	$\displaystyle 0{,}5\cdot\pi\cdot r$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 0{,}5\cdot3{,}14\cdot6\mathrm{cm}$
	$=$	$\displaystyle 9{,}42\ \text{cm}\$

Damit kannst du den gesamten Umfang der Figur berechnen:

$\displaystyle U_F$	$=$	$\displaystyle 2\cdot \text{Radius}+U_{\frac{1}{4}}$
	$=$	$\displaystyle 2\cdot 6\text{cm}+9{,}42\text{cm}$
	$=$	$\displaystyle 21{,}42\text{cm}$

Antwort: Die Figur hat einen Umfang von etwa $21{,}42 \mathrm{cm}$ .

Berechnung des Flächeninhaltes

Die Kreisfläche berechnest du mit der Formel $A=\pi r^2$ .

Die abgebildete Figur ist ein Viertel eines Kreises mit dem Radius $r=6\mathrm{cm}$ . Den Flächeninhalt $A_F$ dieser Figur kannst du demnach mit $A_F=\dfrac{1}{4}\cdot \pi\cdot r^2$ berechnen:

$\displaystyle A_F$	$=$	$\displaystyle =\dfrac{1}{4}\cdot \pi\cdot r^2$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle \dfrac{1}{4}\cdot3{,}14\cdot (6\mathrm{cm})^2$
	$=$	$\displaystyle 28{,}26\mathrm{cm}^2$

Antwort: Die Figur hat einen Flächeninhalt von etwa $28{,}26 \mathrm{cm}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis

Berechnung des Umfangs

Der Umfang der Figur $U_F$ setzt sich aus vier Vierteln eines Kreisumfangs zusammen. Somit ist der Umfang $U_F$ genau der Umfang eines Kreises mit dem Radius $r=6\mathrm{cm}$ .

Die Formel für den Kreisumfang lautet: $U=2\pi r$

Für den Umfang der Figur $U_F$ gilt:

$\displaystyle U_F$	$=$	$\displaystyle 2\cdot\pi\cdot r$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 2\cdot3{,}14\cdot6\mathrm{cm}$
	$=$	$\displaystyle 37{,}68\ \text{cm}\$

Antwort: Die Figur hat einen Umfang von etwa $37{,}68 \mathrm{cm}$ .

Berechnung des Flächeninhaltes

Für die Berechnung des Flächeninhaltes $A_F$ denke dir ein Quadrat mit der Seitenlänge $12\mathrm{cm}$ um die Figur gezeichnet. So wie in der folgenden Abbildung.

Die Quadratfläche $A_Q$ besteht aus vier $\text{\textcolor{660099}{Viertelkreisflächen}}$ und der Fläche der Figur $A_F$ . Die vier $\text{\textcolor{660099}{Viertelkreisflächen}}$ lassen sich zu einer ganzen Kreisfläche $\textcolor{660099}{A_K}$ zusammensetzen, die du mit der Formel $\textcolor{660099}{A_K=\pi r^2}$ berechnen kannst. Dabei beträgt der Radius $r=6\mathrm{cm}$ . Somit erhältst du den Flächeninhalt $A_F$ der Figur als Differenz der Quadratfläche $A_Q$ und der Kreisfläche $\textcolor{660099}{A_K}$ : $A_F=A_Q-\textcolor{660099}{A_K}$

$\displaystyle A_F$	$=$	$\displaystyle (12\mathrm{cm})^2-\textcolor{660099}{\pi\cdot r^2}$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 144 \mathrm{cm}^2-3{,}14\cdot (6\mathrm{cm})^2$
	$=$	$\displaystyle 144\mathrm{cm}^2-113{,}04\mathrm{cm}^2$
	$=$	$\displaystyle 30{,}96\mathrm{cm}^2$

Antwort: Die Figur hat einen Flächeninhalt von etwa $30{,}96\mathrm{cm}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis

Berechnung des Umfangs

Der Umfang $U_F$ der Figur besteht aus zwei $\textcolor{006400}{\text{ grünen Halbkreisen}}$ mit dem Radius $r =2 \text{cm}$ und zwei $\textcolor{660099}{\text{lilafarbigen Strecken}}$ der Länge $b=10\text{cm}$ . Die zwei $\textcolor{006400}{\text{grünen Halbkreise}}$ kannst du zu einem ganzen Kreis zusammensetzen.

Für den Umfang $U_F$ der Figur gilt demnach:

$\displaystyle U_F$	$=$	$\displaystyle \textcolor{006400}{U_K}+\textcolor{660099}{2\cdot b}$
	$=$	$\displaystyle 2\cdot \pi\cdot r+2\cdot b$
	$=$	$\displaystyle 2\cdot \pi \cdot 2\text{cm}+2\cdot 10\text{cm}$
	$=$	$\displaystyle 4\cdot \pi \text{cm}+20\text{cm}$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 4\cdot 3{,}14\text{cm}+20\text{cm}$
	$=$	$\displaystyle 12{,}56 \text{cm}+20 \text{cm}$
	$=$	$\displaystyle 32{,}56 \text{cm}$

Berechnung des Flächeninhaltes

Bei der Berechnung des Flächeninhaltes kannst du die Strategie "Zerlegen" und "Ergänzen" anwenden. Denke dir den linken $\textcolor{660099}{\text{ lilafarbigen}}$ Halbkreis abgeschnitten und auf der rechten Seite wieder eingefügt. Der Flächeninhalt $A_F$ der Figur ist nun genau der Flächeninhalt eines Rechtecks mit den Seitenlängen $a=12\text{cm}-2\text{cm}=10\text{cm}$

und $b=4\text{cm}$ .

Für den Flächeninhalt $A_F$ der Figur gilt demnach:

$\displaystyle A_F$	$=$	$\displaystyle a\cdot b$
	$=$	$\displaystyle 10\text{cm}\cdot 4\text{cm}$
	$=$	$\displaystyle 40\text{cm}^2$

Antwort: Die Figur hat einen Flächeninhalt von $40\mathrm{cm}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis

Berechnung des Umfangs

Zur Verdeutlichung sind in der obigen Abbildung alle Strecken und Halbkreise farbig gekennzeichnet. Der Umfang der Figur $U_F$ setzt sich aus $\textcolor{cc0000}{5\text{ roten}}$ waagrechten Teilstrecken und $\textcolor{cc0000}{6\text{ roten}}$ senkrechten Strecken sowie $\textcolor{006400}{5\; grünen}$ halben Kreisumfängen zusammen. Den Kreisumfang berechnest du mit: $U_K =2\cdot \pi \cdot r$

$\textcolor{cc0000}{5\text{ rote}}$ waagrechte Teilstrecken: $b=(1+2+4+2+1)\mathrm{cm}=10 \mathrm{cm}$

$\textcolor{cc0000}{6\text{ rote}}$ senkrechte Strecken: $h=(1+1+2+2+1+1)\text{cm}=8\text{cm}$

$\textcolor{006400}{\text{2 kleine grüne}}$ Halbkreise (Nr. 1 und 5) ergeben einen ganzen Kreis mit dem Radius $r=0{,}5 \text{cm}\Rightarrow$

$U_1=2\cdot\pi\cdot0{,}5\text{cm}=\pi\text{cm}$

$\textcolor{006400}{\text{2 mittlere grüne}}$ Halbkreise (Nr. 2 und 4) ergeben einen ganzen Kreis mit dem Radius $r=1 \text{cm}\Rightarrow$

$U_2=2\cdot\pi\cdot1\text{cm}=2\pi\text{cm}$

$\textcolor{006400}{\text{1 großer grüner}}$ Halbkreis (Nr. 3) mit dem Radius $r=2 \text{cm}\Rightarrow$

$U_3=\dfrac{1}{2}(2\cdot\pi\cdot2\text{cm})=2\pi\text{cm}$

Damit erhältst du für den gesamten Umfang der Figur:

$\displaystyle U_F$	$=$	$\displaystyle \textcolor{cc0000}{b+h}+\textcolor{006400}{U_1+U_2+U_3}$
	$=$	$\displaystyle 10\text{cm}+8\text{cm}+(\pi+2\pi+2\pi)\text{cm}$
	$=$	$\displaystyle 18\text{cm}+5\pi\text{cm}$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 18\text{cm}+5\cdot 3{,}14\text{cm}$
	$=$	$\displaystyle 33{,}7\text{cm}$

Antwort: Die Figur hat einen Umfang von etwa $33{,}7 \mathrm{cm}$ .

Berechnung des Flächeninhaltes

Zur Verdeutlichung sind in der obigen Abbildung die 5 Quadrate nicht mehr farbig gekennzeichnet. Der Flächeninhalt der Figur setzt sich aus der Fläche der 5 weißen Quadrate und der Fläche von $\textcolor{006400}{\text{5 grünen}}$ Halbkreisen zusammen. Bei den Quadraten sind jeweils 2 gleich groß. Je 2 Halbkreise lassen sich zu einem ganzen Kreis ergänzen.

Den Flächeninhalt eines Quadrates berechnest du mit $A_Q=a^2$ . Berechne nun den Flächeninhalt der 5 weißen Quadrate:

$\displaystyle A_Q$	$=$	$\displaystyle A_1+A_2+A_3+A_4+A_5$
	↓	$A_1=A_5$ und $A_2=A_4$
	$=$	$\displaystyle 2\cdot(1\text{cm})^2+2\cdot(2\text{cm})^2+(4\text{cm})^2$
	$=$	$\displaystyle (2+8+16)\text{cm}^2$
	$=$	$\displaystyle 26 \text{cm}^2$

Den Flächeninhalt eines Kreises kannst du mit $A_K=\pi\cdot r^2$ berechnen. Berechne nun den Flächeninhalt der $\textcolor{006400}{\text{5 grünen}}$ Halbkreise:

$\textcolor{006400}{\text{2 kleine grüne}}$ Halbkreise (Nr. 1 und 5) ergeben einen ganzen Kreis mit dem Radius $r=0{,}5 \text{cm}\Rightarrow$

$A_{K1}=\pi\cdot(0{,}5\text{cm})^2=0{,}25\pi\text{cm}^2$

$\textcolor{006400}{\text{2 mittlere grüne}}$ Halbkreise (Nr. 2 und 4) ergeben einen ganzen Kreis mit dem Radius $r=1 \text{cm}\Rightarrow$

$A_{K2}=\pi\cdot(1\text{cm})^2=\pi\text{cm}^2$

$\textcolor{006400}{\text{1 großer grüner}}$ Halbkreis (Nr. 3) mit dem Radius $r=2 \text{cm}\Rightarrow$

$A_{K3}=\dfrac{1}{2}(\pi\cdot(2\text{cm})^2)=2\pi\text{cm}^2$

$\displaystyle \textcolor{006400}{A_K}$	$=$	$\displaystyle \textcolor{006400}{A_{K1}+A_{K2}+A_{K3}}$
	$=$	$\displaystyle \textcolor{006400}{(0{,}25\pi+\pi+2\pi)\text{cm}^2}$
	$=$	$\displaystyle \textcolor{006400}{3{,}25 \pi\text{cm}^2}$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle \textcolor{006400}{3{,}25\cdot 3{,}14\text{cm}^2}$
	$=$	$\displaystyle \textcolor{006400}{10{,}205\text{cm}^2}$
	$≈$	$\displaystyle \textcolor{006400}{10{,}21\text{cm}^2}$

Damit erhältst du für den gesamten Flächeninhalt der Figur:

$\displaystyle A_F$	$=$	$\displaystyle A_Q+\textcolor{006400}{A_K}$
	$=$	$\displaystyle 26\text{cm}^2+\textcolor{006400}{10{,}21\text{cm}^2}$
	$=$	$\displaystyle 36{,}21\text{cm}^2$

Antwort: Die Figur hat einen Flächeninhalt von etwa $36{,}21\mathrm{cm}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Eine Firma produziert runde Tischdecken. Jede Tischdecke erhält um ihren Rand ein gemustertes Band (dieses Band wird auch Borte genannt). Berechne jeweils die Länge des gemusterten Bandes. Gib die Länge in Metern ( $\text{m}$ ) gerundet auf zwei Stellen nach dem Komma an.

Der Durchmesser beträgt $150\,\text{cm}$ .

Der Durchmesser beträgt $1700\,\text{mm}$ .

Der Durchmesser beträgt $2{,}10\,\text{m}$ .

Eine Näherin hat ein gemustertes Band mit einer bestimmten Länge abgeschnitten. Dieses Band soll um den Rand einer runden Tischdecke genäht werden. Welchen Durchmesser hat die jeweils dazugehörende runde Tischdecke. Gib den Durchmesser in Metern $\left(\text{m}\right)$ gerundet auf zwei Stellen nach dem Komma an.

Das gemustertes Band hat eine Länge von $6{,}28\,\text{m}$ .

Das gemustertes Band hat eine Länge von $785\,\text{cm}$ .

Das gemustertes Band hat eine Länge von $10990\,\text{mm}$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle b$	$=$	$\displaystyle 2\cdot\pi\cdot r\cdot\frac{\alpha}{360^{\circ}}$
	↓	Setze $r=5\;\text{cm}$ und $\varphi =45^\circ$ ein.
	$=$	$\displaystyle 2\cdot\pi\cdot5\;\text{cm}\cdot\frac{45^\circ}{360^{\circ}}$
	↓	Fasse zusammen.
	$=$	$\displaystyle \frac{5}{4}\pi\;\text{cm}$
	$≈$	$\displaystyle 3{,}93\;\text{cm}$

$\displaystyle A_S$	$=$	$\displaystyle \pi\cdot r^2\cdot\frac{\alpha}{360^{\circ}}$
	↓	Setze $r=5\;\text{cm}$ und $\varphi =45^\circ$ ein.
	$=$	$\displaystyle \pi\cdot \left(5\;\text{cm}\right)^2\cdot\frac{45^{\circ}}{360^{\circ}}$
	↓	Fasse zusammen.
	$=$	$\displaystyle \frac{25}{8}\pi\;\text{cm}^2$
	$≈$	$\displaystyle 9{,}82\;\text{cm}^2$

$\displaystyle U$	$=$	$\displaystyle d \cdot \pi$	$\displaystyle : \pi$
$\displaystyle \dfrac{U}{\pi}$	$=$	$\displaystyle d$

$\displaystyle U$	$=$	$\displaystyle d \cdot \pi$	$\displaystyle : \pi$
$\displaystyle \dfrac{U}{\pi}$	$=$	$\displaystyle d$

$\displaystyle U$	$=$	$\displaystyle d \cdot \pi$	$\displaystyle : \pi$
$\displaystyle \dfrac{U}{\pi}$	$=$	$\displaystyle d$

$\displaystyle U_F$	$=$	$\displaystyle 2\cdot16\mathrm{cm}+2\cdot\pi\cdot3\mathrm{cm}$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 2\cdot16\mathrm{cm}+2\cdot3{,}14\cdot3\mathrm{cm}$
	$=$	$\displaystyle 50{,}84\ \text{cm}\$

$\displaystyle U_F$	$=$	$\displaystyle \textcolor{009999}{U_{großer Kreis}}+U_{kleiner Kreis}$
	$=$	$\displaystyle 2\cdot\pi\cdot6\mathrm{cm}+2\cdot\pi\cdot2\mathrm{cm}$
	↓	$\pi$ $\approx$ 3,14
	$≈$	$\displaystyle 2\cdot 3{,}14\cdot 6\ \text{cm}\ +2\cdot 3{,}14\cdot 2\ \text{cm}$
	$=$	$\displaystyle 37{,}68\text{cm}+12{,}56 \text{cm}$	$\displaystyle$
	$=$	$\displaystyle 50{,}24\text{cm}$

$\displaystyle U_F$	$=$	$\displaystyle 2 \cdot U_K$
	$=$	$\displaystyle 2\cdot(2 \cdot\pi\cdot4\mathrm{cm})$
	↓	$\pi$ $\approx$ 3,14
	$≈$	$\displaystyle 4\cdot 3{,}14\cdot 4\ \text{cm}\$
	$=$	$\displaystyle 50{,}24\text{cm}$

$\displaystyle U_F$	$=$	$\displaystyle \textcolor{ff6600}{\frac{1}{2}\cdot U}+\textcolor{660099}{\text{ U}}$
	$=$	$\displaystyle \textcolor{ff6600}{ \frac{1}{2}\cdot (2\cdot\pi \cdot r_1) }+\textcolor{660099}{{ 2\cdot\pi \cdot r_2}}$
	$=$	$\displaystyle \textcolor{ff6600}{ \frac{1}{2}\cdot (2\cdot\pi \cdot 5\text{cm}) }+\textcolor{660099}{{ 2\cdot\pi \cdot 2{,}5\text{cm}}}$
	$=$	$\displaystyle \textcolor{ff6600}{ \pi \cdot 5\text{cm} }+\textcolor{660099}{{ \pi \cdot 5\text{cm}}}$
	$=$	$\displaystyle 10\cdot \pi \text{cm}$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 10\cdot 3{,}14 \text{cm}$
	$=$	$\displaystyle 31{,}4 \text{cm}$

$\displaystyle A_F$	$=$	$\displaystyle \frac{1}{2}\cdot A_K$
	$=$	$\displaystyle \frac{1}{2}\cdot\pi\cdot r_1^2$
	$=$	$\displaystyle \frac{1}{2}\cdot\pi\cdot (5 \text{cm})^2$
	$=$	$\displaystyle \frac{1}{2}\cdot\pi\cdot 25 \text{cm}^2$
	$=$	$\displaystyle 12{,}5\cdot\pi \text{cm}^2$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 12{,}5\cdot 3{,}14 \text{cm}^2$
	$=$	$\displaystyle 39{,}25 \text{cm}^2$

$\displaystyle U$	$=$	$\displaystyle d\cdot \pi$
	↓	$\pi \approx 3{,}14$
	$≈$	$\displaystyle 150\, \text{cm}\cdot 3{,}14$
	$=$	$\displaystyle 471\, \text{cm}$
	↓	Umrechnung 100 cm sind 1 m
	$=$	$\displaystyle 4{,}71\, \text{m}$

Aufgaben zur Berechnung von Kreisringen und Kreissektoren

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

﻿

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1. Möglichkeit: Mit dem Radius und dem Mittelpunktswinkel

2. Möglichkeit: Mit dem Radius und der Länge des Kreisbogens

Hast du eine Frage oder Feedback?

Alternativ

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?