Manchmal ist es notwendig, die Lösungen einer quadratischen Gleichung, die einen oder mehrere Parameter enthält, mithilfe der Mitternachtsformel zu berechnen.
Die Aufgabe liegt darin, durch Umformen und Ausklammern die Gleichung auf die Form zu bringen, die Koeffizienten , und , die von den Parametern abhängen, richtig abzulesen und dann mit ihnen korrekt weiterzurechnen.
Allgemeine Vorgehensweise
Wenn man auf eine quadratische Gleichung mit Parameter die Mitternachtsformel anwenden will, geht man folgendermaßen vor:
1. Teil: Gleichung auf die richtige Form bringen
1. Schritt | Genau wie bei quadratischen Gleichungen ohne Parameter muss die Gleichung zunächst so umgeformt werden, dass auf der einen Seite 0 steht. Klammern müssen aufgelöst und Zusammengehöriges (wie z. B. zu ) zusammengefasst sein. |
|---|---|
2. Schritt | Aus den Termen, bei denen steht, wird ausgeklammert. Aus den Termen, bei denen steht, wird ausgeklammert. |
3. Schritt: | ist der Faktor, der bei steht (ohne das selbst); ist der Faktor, der bei steht (ohne das selbst); ist der Term, der ohne dasteht. |
Sonderfall: a=0 für bestimmte Parameter
Falls für bestimmte Parameterwerte gleich null wird, muss man diese Werte in Teil gesondert betrachten. Für alle anderen Werte fährt man mit Teil und fort.
2. Teil: Diskriminante berechnen und Fallunterscheidung durchführen
1. Schritt | Man berechnet die Diskriminante mit Hilfe der Formel . |
|---|---|
2. Schritt | Man überprüft die Diskriminante in Abhängigkeit der / des Parameter/s auf ihr Vorzeichen. Dadurch erhält man eine Aussage darüber, wie viele Lösungen die Gleichung besitzt, falls der Parameter einen bestimmten Wert annimmt. |
3. Teil: Mitternachtsformel anwenden und Lösungen angeben
Nun wendet man die Mitternachtsformel an.
Sonderfall a=0
Hier setzt man die Parameterwerte, für die wird, in die Ausgangsgleichung ein und löst jeweils die sich ergebende lineare Gleichung
Beispiele
Da es sehr viele kleine Details zu beachten gilt, versteht man das Prinzip am besten, wenn man sich möglichst viele Beispiele dazu ansieht und durchrechnet.
Beispiel mit einem Parameter
Aufgabenstellung: Löse die Gleichung in Abhängigkeit vom Parameter m.
| ↓ | 1.Teil, 1. Schritt: Bringe alles auf eine Seite. | ||
| ↓ | 1.Teil, 2. Schritt: Klammere x aus . | ||
| ↓ | 1.Teil, 3. Schritt: Lies a, b und c ab. | ||
. Teil, . Schritt: Berechne die Diskriminante ; dabei ist die erste binomische Formel nützlich.
| ↓ | |||
| ↓ | Binomische Formel anwenden und zusammenfassen. | ||
. Teil, . Schritt: Untersuche das Vorzeichenverhalten der Diskriminante, indem du sie gleich null setzt und mithilfe der Mitternachtsformel die Nullstellen berechnest.
Immer noch . Teil, . Schritt: Da eine nach oben geöffnete Parabel ist, ist die Diskriminante für und positiv, für und gleich null und für negativ.
Gib nun mit diesem Ergebnis die Anzahl der Lösungen in Abhängigkeit vom Parameter an.
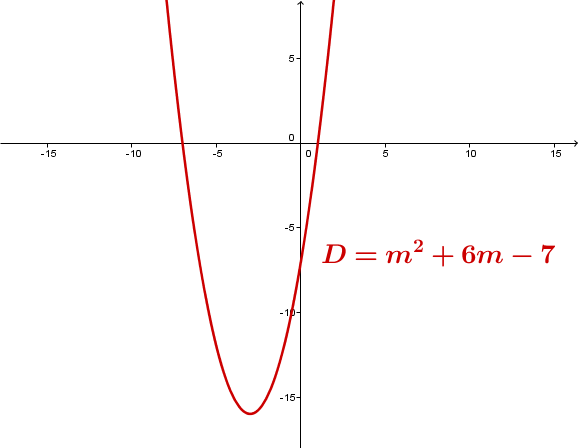
oder : Zwei Lösungen
oder : Eine Lösung
: Keine Lösung
. Teil: Berechne nun mithilfe der Mitternachtsformel die Lösungen in Abhängigkeit vom Parameter .
oder
oder :
Keine Lösung
Beispiel mit zwei Parametern
Aufgabenstellung: Löse die Gleichung in Abhängigkeit von den Parametern .
mit
In diesem Fall lässt du den ersten und zweiten Schritt des . Teils weg, da das Format der Gleichung schon passt, weshalb du jetzt schon , und abliest.
. Teil, . Schritt: Berechne die Diskriminante .
. Teil, . Schritt: Untersuche das Vorzeichenverhalten der Diskriminante, indem du die Parameter betrachtest.
Immer noch . Teil, . Schritt: Lies am Verhalten der Parameter (und damit der Diskriminanten) ab, wie viele Lösungen die Gleichung besitzt.
: zwei Lösungen
: eine Lösung
: keine Lösung
. Teil: Berechne nun mithilfe der Mitternachtsformel die Lösungen in Abhängigkeit der Parameter und .
:
: keine Lösung
Beispiel mit einem Sonderfall
Aufgabenstellung: Löse die Gleichung in Abhängigkeit vom Parameter .
| ↓ | 1.Teil, 1. Schritt: Bringe alles auf eine Seite und fasse zusammen. | ||
| ↓ | 1.Teil, 2. Schritt: Klammere aus . | ||
| ↓ | 1.Teil, 3. Schritt: Lies a, b und c ab. | ||
Im Sonderfall fällt der Term mit weg und es ergibt sich eine lineare Gleichung ; diesen Fall betrachtest du unten gesondert.
Sei nun zunächst .
. Teil, . Schritt: Berechne die Diskriminante ; dabei ist die erste binomische Formel nützlich
. Teil, . Schritt: Untersuche das Vorzeichenverhalten der Diskriminante: Diese ist hier immer positiv, da immer größer oder gleich null ist und deshalb immer echt größer als Null ist.
Immer noch . Teil, . Schritt: Lies aus dem Vorzeichenverhalten der Diskriminante die Anzahl der Lösungen ab.
Für alle gilt zwei Lösungen unabhängig von .
. Teil: Berechne nun mithilfe der Mitternachtsformel die Lösungen in Abhängigkeit vom Parameter .
Sei nun .
In diesem Fall erhältst du eine lineare Gleichung. Setze dazu ein und löse auf.
