Aufgaben mit zwei Unbekannten
Hier findest du gemischte Aufgaben zu linearen Gleichungssystemen mit zwei Unbekannten. Lerne, verschiedene Verfahren anzuwenden!
- 1
Teste dein Wissen!
Ordne die Schritte des Gleichsetzungsverfahrens richtig ein! Trage dafür in das Lösungsfeld die Nummern der Schritte nacheinander und ohne Leerzeichen ein (z. B. 123).
Die Variable in eine Gleichung einsetzen.
Die Gleichungen und gleichsetzen.
Die entstandene Gleichung nach einer Variable auflösen.
Welche der folgenden Aussagen beschreibt einen Schnittpunkt?
Warum brauchst du ein lineares Gleichungssytem?
- 2
Löse die Gleichungssysteme.
Gib die Lösungsmenge in der Form in das Eingabefeld ein. Beispiel:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Lineares Gleichungssystem mit Gleichsetzungsverfahren
1. Beide Gleichungen nach y auflösen
Löse beide Gleichungen nach einer Variablen auf. In diesem Fall ist schon einzeln, also ist es einfacher nach aufzulösen.
2. Gleichsetzen
Setze die beiden Gleichungen und gleich.
3. Gleichung nach x auflösen
4. x einsetzen, um y heraus zu finden
Setze in oder ein.
Gib die Lösungsmenge an.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Lineares Gleichungssystem mit Gleichsetzungsverfahren
1. Beide Gleichungen nach x auflösen
Löse beide Gleichungen nach einer Variablen auf. Zum Beispiel nach der Variablen .
2. Gleichsetzen
Setze die beiden Gleichungen und gleich.
3. Gleichung nach y auflösen
4. einsetzen, um heraus zu finden
in einsetzen
Gib die Lösungsmenge an
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Lineares Gleichungssystem mit Gleichsetzungsverfahren
1. Beide Gleichungen nach einer Variable auflösen
Löse beispielsweise nach auf
2. Gleichsetzen
Setze und gleich.
3. Nach der einen Variable auflösen
Löse nach auf.
4. In eine Gleichung einsetzten, um die andere Variable heraus zu finden
Setze beispielsweise in ein.
wird für eingesetzt.
Lösungsmenge angeben!
Hast du eine Frage oder Feedback?
- 3
Löse die Linearen Gleichungssysteme mit dem Einsetzungsverfahren.
Gib die Lösungsmenge in der Form in das Eingabefeld ein. Beispiel:
Brüche werden mit einem "/" angegeben. Beispiel: sind im Eingabefeld 3/8.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Als erstes musst du eine der beiden Gleichungen nach einer Variablen auflösen. In diesem Fall erkennst du, dass Gleichung schon nach aufgelöst ist.
Setze aus Gleichung in ein
Multipliziere die Klammer aus und löse nach auf.
Setze aus Gleichung in ein
↓ Kürze den linken Bruch mit 3 und schreibe 4 als Bruch.
↓ Erweitere mit 3, um die Brüche zu addieren.
↓ Addiere die Brüche
Gib zum Schluss die Lösungsmenge an.
.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Als erstes musst du eine der beiden Gleichungen nach oder auflösen. Es bietet sich hier an, Gleichung nach umzustellen.
Stelle Gleichung nach um.
Setze aus Gleichung in ein
Multipliziere die Klammer aus und löse nach auf.
Setze in die umgeformte zweite Gleichung ein, um zu bestimmen.
Gib nun noch die Lösungsmenge an.
.
Hast du eine Frage oder Feedback?
- 4
Löse das folgende Gleichungssystem mit dem Additions-/Subtraktionsverfahren!
Gib die Lösungsmenge in der Form in das Eingabefeld ein. Beispiel:
Brüche werden mit einem "/" im Eingabefeld eingegeben. Beispiel: wird zu 3/8.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Additions-/ Subtraktionsverfahren
0. Schritt: Aufräumen der Gleichungen und Auswahl einer Variablen
Da die Gleichungen schon schön geordnet sind fällt dieser Punkt weg. In diesem Fall ist es gleich aufwendig die Aufgabe zu lösen, egal ob du oder auswählst.
Die Lösung wird für die Variable vorgerechnet.
1. Schritt: Vervielfachen der Gleichungen
In Gleichung sind es , in Gleichung sind es . Ein gemeinsames Vielfaches ist also . Multipliziere dafür die erste Gleichung mit und die zweite Gleichung mit .
Gleichung 1
Gleichung 2
2. Schritt: Entfernung einer Variablen durch Addition/Subtraktion
Die Vorzeichen der ausgesuchten Variable sind beide Male gleich. Deswegen musst du das Subtraktionsverfahren anwenden.
3. Schritt: Werte der beiden Variablen bestimmen
Wert von bestimmen
Wert von bestimmen: Einsetzen von in
Die Lösung ist also und : .
- 5
Teste dein Wissen! Mit welchen Verfahren ist es sinnvoll die folgenden Gleichungssysteme zu lösen?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Die Gleichung ist bereits nach aufgelöst. Es bietet sich also an, das Einsetzungsverfahren zu verwenden.
Bei den anderen beiden Verfahren müssen noch Umformungsschritte vorgenommen werden, bevor man sie anwenden kann.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Alle drei Verfahren können direkt angewendet werden und sind daher sinnvoll. Am einfachsten ist aber hier das Gleichsetzungsverfahren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
In Gleichung steht , in Gleichung . Da bei Addition das wegfällt, eignet sich das Additionsverfahren.
Bei den anderen beiden Verfahren müssen noch Umformungsschritte vorgenommen werden, bevor man sie anwenden kann.
Hast du eine Frage oder Feedback?
- 6
Löse mit dem am besten geeigneten Verfahren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
In dieser Aufgabe bietet sich das Additions-/Subtraktionsverfahren an. Du verwendest das Subtraktionsverfahren, da in beiden Gleichungen vorkommt.
Löse nach auf
Setze in eine der Gleichungen ein
in
Bestimme die Lösungsmenge.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Eine sehr schöne Lösung ergibt sich mit dem Einsetzungsverfahren.
Die Gleichung ist nach aufgelöst und in Gleichung steht . Du kannst sogar ohne Umformung das Einsetzungsverfahren verwenden.
Schreibe Gleichung um.
Setze aus Gleichung in Gleichung ein.
Fasse zusammen und löse nach auf.
Wie du jetzt sehen kannst, gleichen sich die Ergebnisse nicht wodurch sich ein Widerspruch ergibt. Daraus folgt, dass das LGS keine Lösungen hat, da für keine Zahl zugeordnet werden kann.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Du verwendest am Besten das Additionsverfahren, da du mit einem scharfen Blick siehst, dass das -fache von ist.
Vervielfache die erste Gleichung
Wie du jetzt sehen kannst, sind beide Gleichungen identisch. Daraus folgt, dass das LGS unendlich viele Lösungen hat. Graphisch betrachtet können das zwei Geraden sein, die aufeinander liegen.
Löse die Gleichung noch nach einer Variablen auf um die Lösungsmenge anzugeben.
Hast du eine Frage oder Feedback?
- 7
Bestimmen Sie die Lösungsmengen folgender Gleichungssysteme.
Gib die Lösungsmenge in der Form in das Eingabefeld ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
In diesem Fall ist das Einsetzungsverfahren sinnvoll, da die zweite Gleichung bereits nach einer Variablen aufgelöst ist.
Setz die Gleichung in ein.
Lös nach auf.
Nun kannst du in einsetzen und nach auflösen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineares Gleichungssystem
In diesem Fall ist das Einsetzungsverfahren sinnvoll, da die zweite Gleichung bereits nach einer Variablen aufgelöst ist.
Setz die Gleichung in ein.
Löse nach auf.
Setz in ein und löse nach auf.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineares Gleichungssystem
In diesem Fall ist das Einsetzungsverfahren sinnvoll, da die zweite Gleichung bereits nach einer Variablen aufgelöst ist.
Setz die Gleichung in ein.
Lös nach auf.
Setz nun in ein und lös nach auf.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineares Gleichungssystem
Lösung mit Einsetzungsverfahren
In diesem Fall ist das Einsetzungsverfahren sinnvoll, da die zweite Gleichung bereits nach einer Variablen aufgelöst ist.
Teile durch 2, um nach der Variablen aufzulösen.
Setze in ein.
in eingesetzt:
Löse dann nach auf.
Setze anschließend in ein und löse nach auf.
in eingesetzt:
Alternative Lösung: Gleichsetzungsverfahren
Eine weitere Möglichkeit ist, hier das Gleichsetzungsverfahren anzuwenden, da auf der linken Seite von und auf der rechten Seite von fast der gleiche Term steht.
Multipliziere mit , um auf der rechten Seite zu erzeugen.
Setze die rechte Seite von mit der linken von gleich und löse nach auf.
Setze in (oder auch ) ein und löse nach auf.
Alternative Lösung: Kombination Additionsverfahren und Einsetzverfahren
Auch das Additionsverfahren kann hier sinnvoll eingesetzt werden. Dazu stellt man die Gleichungen zunächst so um, dass die passenden Terme untereinander stehen:
Subtrahiere die zweite von der ersten Gleichung.
Da die erste Gleichung nun nach aufgelöst ist, kann man wieder das Einsetzungsverfahren anwenden.
Setze dazu in ein und löse nach auf.
Setze in ein und löse nach auf.
Hast du eine Frage oder Feedback?
- 8
Löse die folgenden Gleichungssysteme mit 2 Gleichungen und 2 Variablen zunächst graphisch und dann rechnerisch.
Gib die Lösungsmenge in der Form in das Eingabefeld ein. Beispiel:
Brüche werden mit einem "/" in das Eingabefeld eingegeben. Beispiel: wird zu 3/8.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichunssysteme
Lineares Gleichungssystem mit zwei Unbekannten
Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen), die alle erfüllt werden sollen, zusammen.
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.

Der Schnittpunkt liegt bei und . Somit lautet die Lösungsmenge .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Du kannst nun die Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Lineares Gleichungssystem mit zwei Unbekannten
Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen), die alle erfüllt werden sollen, zusammen.
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.

Der Schnittpunkt liegt bei und . Somit lautet die Lösungsmenge .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Du kannst nun die Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Lineares Gleichungssystem mit zwei Unbekannten
Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen), die alle erfüllt werden sollen, zusammen.
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
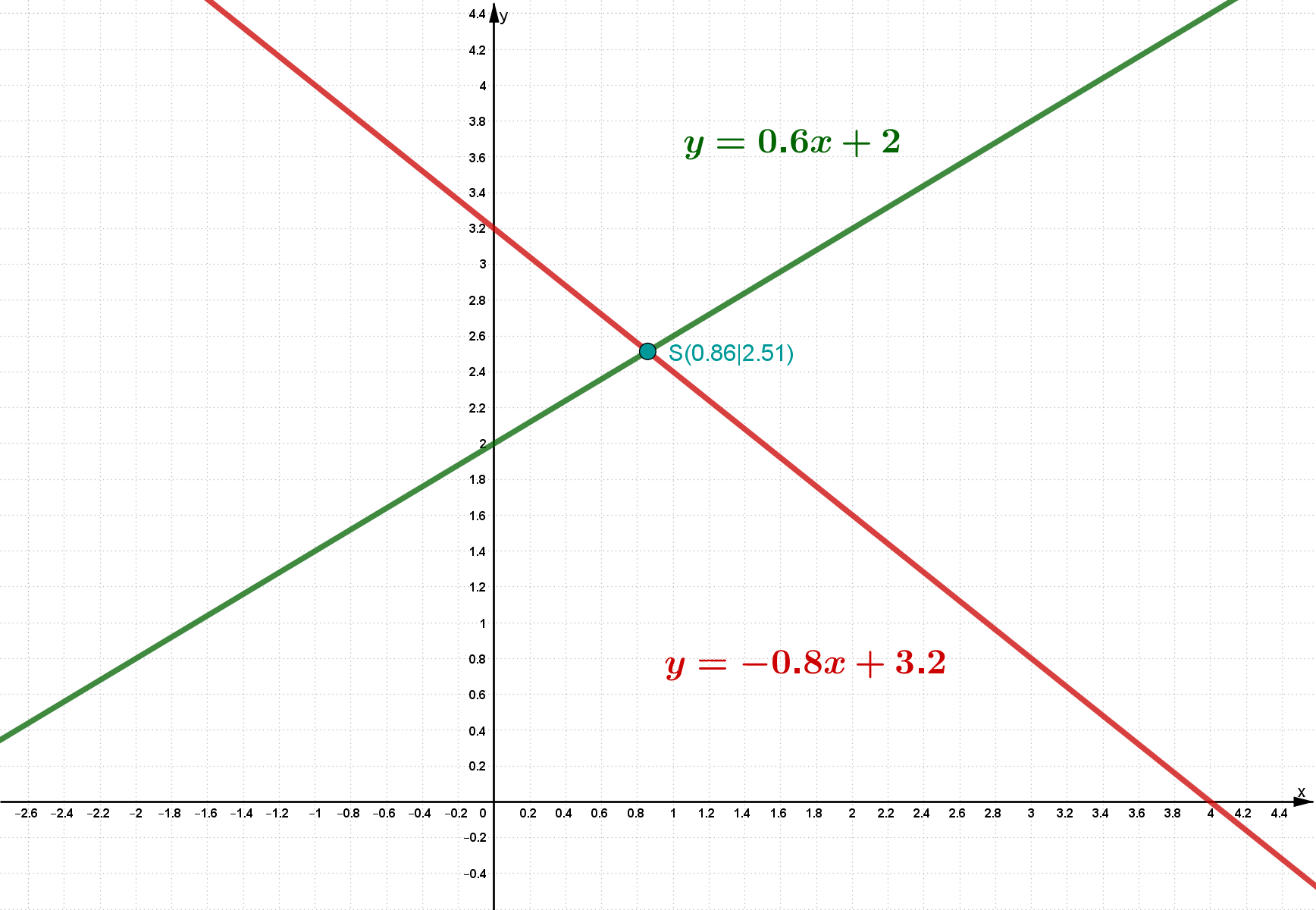
Der Schnittpunkt liegt bei und . Somit lautet die Lösungsmenge .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Du kannst nun die Lösungsmenge angeben.
Hast du eine Frage oder Feedback?
- 9
Teste dein Wissen!
Welche der folgenden Systeme ist ein lineares Gleichungssystem? Markiere alle zutreffenden Antworten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungsystem
Überlege dir, was ein lineares Gleichungssystem überhaupt ist:
Mehrere Gleichungen, die gleichzeitig erfüllt sein müssen, nennt man Gleichungssystem.
Wenn zusätzlich noch jede Variable höchstens mit dem Exponenten auftaucht, wird es Lineares Gleichungssystem genannt.
Überprüfe nun die beiden Kriterien.
Du erkennst, dass…
… kein Lineares Gleichungssystem ist, weil in der ersten Gleichung sowohl als auch den Exponenten haben.
Du erkennst weiter, dass…
… kein Lineares Gleichungssystem ist, weil in der zweiten Gleichung mit dem Exponenten auftaucht.
In allen anderen Fällen sind beide Kriterien erfüllt. Es handelt es sich somit um lineare Gleichungssysteme.
Hast du eine Frage oder Feedback?
Wie viele Lösungen hat folgendes lineares Gleichungssystem?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lösbarbarkeit von Gleichungssystemen
Du zeigst, dass die Gleichungen und nicht gleichzeitig erfüllt sein können. Dabei verwendest du am besten das Subtraktionsverfahren.
Subtrahiere Gleichung von Gleichung .
Die Gleichung ist offensichtlich falsch. Damit ist auch das gegebene Gleichungssystem falsch und hat keine Lösung.
Die Lösungsmenge ist somit .
Hast du eine Frage oder Feedback?
Wie viele Lösungen hat folgendes Gleichungssystem?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lösbarkeit von Gleichungssystemen
Du zeigst, dass die Gleichungen und äquivalent sind. Das heißt, jedes und , das Gleichung löst, liefert auch für Gleichung eine wahre Aussage.
Eine Möglichkeit, dies zu zeigen, ist das Einsetzungsverfahren.
Stelle zunächst Gleichung nach y um.
Setze nun in Gleichung ein. Du erhältst die neue Gleichung .
Fasse die linke Seite der Gleichung zusammen.
Die Gleichung ist wahr und zwar unabhängig von . Es gibt also unendlich viele Lösungen.
Hast du eine Frage oder Feedback?
Wie viele Lösungen hat folgendes lineares Gleichungssystem?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lösbarkeit der Gleichungssysteme
Ein lineares Gleichungssystem hat genau eine Lösung, wenn es eindeutig nach und aufgelöst werden kann.
Um das herauszufinden, bietet sich das Einsetzungsverfahren an, da man zum Beispiel Gleichung sehr einfach nach umstellen kann.
Stelle zunächst Gleichung nach um.
Setze nun in Gleichung ein. Du erhältst die neue Gleichung .
Fasse die linke Seite zusammen.
Löse nach auf.
zum Beispiel in Gleichung ein, um zu bestimmen.
Löse nach auf.
Es gibt also genau eine Lösung.
Hast du eine Frage oder Feedback?
- 10
Bestimme die Lösungsmengen folgender linearer Gleichungssysteme.
Gib die Lösungsmenge in der Form in das Eingabefeld ein. Beispiel:
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Lineare Gleichungssysteme kannst du mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren lösen.
Mit den verschiedenen Lösungsverfahren kannst du wie folgt die Lösung berechnen. Das Einsetzungsverfahren eignet sich hier aber am Besten.
Einsetzungsverfahren
Hier die Lösung mit dem Einsetzungsverfahren:
Gegeben:
Gleichung ist nach aufgelöst. Dieser Term kommt auch in Gleichung vor. Setze also die Gleichung in ein.
↓ Aus Gleichung : einsetzen.
↓ Löse die Klammer auf.
↓ Löse nach auf.
Um zu finden, setze den Wert von in ein.
↓ Setze ein.
Gib die Lösungsmenge an, dabei zuerst die Lösung für , dann für eintragen.
Lösung mithilfe der anderen Verfahren
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Lineare Gleichungssysteme kannst du mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren lösen.
Mit den verschiedenen Lösungsverfahren kannst du wie folgt die Lösung berechnen. Das Einsetzungsverfahren eignet sich hier am Besten.
Einsetzungsverfahren
Hier die Lösung mit dem Einsetzungsverfahren:
Gegeben:
Forme so um, dass auf der einen Seite steht.
Setze in ein und löse nach auf.
↓ Setze ein.
↓ Berechne die Brüche.
Setze in ein.
↓ Setze ein.
Gib die Lösungsmenge an, dabei zuerst die Lösung für , dann für .
Lösung mithilfe anderer Verfahren
Hast du eine Frage oder Feedback?
- 11
Ein Hotel verfügt über 105 Betten, die sich in 40 Zwei-bzw.-Dreibettzimmern befinden. Wie viele Zwei-und-Dreibettzimmer kann das Hotel vermieten?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Gleichungen aus dem Text aufstellen
Was ist bekannt? Die Summe der Anzahl der Zweibettzimmer und der Anzahl der Dreibettzimmer beträgt 40. Diese Aussage liefert dir Gleichung :
In einem Zweibettzimmer stehen zwei Betten. In Zweibettzimmern stehen somit Betten und entsprechend stehen in den Dreibettzimmern Betten. Insgesamt hat das Hotel 105 Betten, so dass du Gleichung aufstellen kannst:
Du hast nun folgendes lineare Gleichungssystem mit zwei Gleichungen und zwei Unbekannten erhalten:
Gleichungssystem lösen
Zur Lösung dieses Gleichungssystems stehen dir drei Lösungsverfahren zur Verfügung:
Lösung mit dem Einsetzungsverfahren
Löse Gleichung nach einer der beiden Variablen auf und setze diese Variable in Gleichung ein. Es spielt keine Rolle, ob du nach oder auflöst.
. Eingesetzt in
Setze in Gleichung ein:
Die Lösungsmenge deines Gleichungssystems lautet also :
Antwort: Das Hotel verfügt über Zweibettzimmer und über Dreibettzimmer.
Lösung mit dem Gleichsetzungsverfahren
Löse beide Gleichungen nach derselben Variablen auf. Du hast beim Einsetzungsverfahren schon Gleichung nach aufgelöst.
. Nun muss Gleichung auch nach aufgelöst werden:
Setze nun die beiden rechten Seiten der Gleichungen und gleich:
Setze in Gleichung ein:
Die Lösungsmenge deines Gleichungssystems lautet also :
Antwort: Das Hotel verfügt über Zweibettzimmer und über Dreibettzimmer.
Lösung mit dem Additionsverfahren
Ziel ist es, dass sich durch Addition der beiden Gleichungen eine der unbekannten Größen aufhebt. In diesem Gleichungssystem kannst du z.B. die Gleichung mit multiplizieren . Durch Addition der beiden Gleichungen und erhältst du schon die Lösung für :
Setze in Gleichung ein:
Die Lösungsmenge deines Gleichungssystems lautet also :
Antwort: Das Hotel verfügt über Zweibettzimmer und über Dreibettzimmer.
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable für die Anzahl der Zweibettzimmer und die Variable für die Anzahl der Dreibettzimmer.
- 12
Ein Bauer hält in seinem Stall Hühner und Kaninchen. Er zählt insgesamt 120 Beine. Es gibt dreimal mehr Hühner als Kaninchen. Wie viele Hühner und Kaninchen hat der Bauer?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Gleichungen aus dem Text aufstellen
Die Anzahl der Hühner bezeichnest du mit der Variablen und mit der Variablen die Anzahl der Kaninchen. Was ist bekannt? Ein Huhn hat zwei Beine, ein Kaninchen hat vier Beine. Somit haben Hühner Beine und Kaninchen haben Beine. Diese Aussage liefert dir Gleichung :
"Es gibt dreimal mehr Hühner als Kaninchen" muss als Gleichung formuliert werden. Da die Anzahl der Kaninchen ist, musst du mit multiplizieren um die Anzahl der Hühner zu erhalten. Du kannst nun Gleichung aufstellen:
Du hast nun folgendes lineare Gleichungssystem mit zwei Gleichungen und zwei Unbekannten erhalten:
Zur Lösung dieses Gleichungssystems stehen dir drei Lösungsverfahren zur Verfügung:
Hier bietet sich das Einsetzungsverfahren an, da Gleichung schon nach der Variablen aufgelöst ist.
Lösung mit dem Einsetzungsverfahren
Setze Gleichung in Gleichung ein:
Setze in Gleichung ein:
Die Lösungsmenge deines Gleichungssystems lautet also :
Antwort: Der Bauer besitzt Hühner und Kaninchen.
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable für die Anzahl der Hühner und die Variable für die Anzahl der Kaninchen.
- 13
Bestimme die Lösungsmengen folgender nicht-linearer Gleichungssysteme.
Gib die Lösungsmenge in der Form in das Eingabefeld ein. Beispiel:
wobei
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Lineare Gleichungssysteme kannst du mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren lösen.
Probiere diese Verfahren für dieses nicht-lineare Gleichungssystem aus.
Hier eignet sich das Additionsverfahren. Wenn man die beiden Gleichungen so umformt, dass die Terme mit oder identisch sind, kann man die beiden umgeformten Gleichungen voneinander abziehen und muss nur noch eine Gleichung mit einer Variablen lösen.
Lösung mithilfe des Additionsverfahren
Mit dem Additionsverfahren kommst du auf diese Lösung:
Gegeben:
Die Gleichung enthält den Term und die Gleichung ein Vielfaches von und zwar . Nimm also mal und addiere dann die Gleichungen, um den Term zu eliminieren.
Das neue Gleichungssystem lautet also:
:
Löse nun die neu entstandene Gleichung nach auf.
↓ Bilde die Kehrbrüche.
Setze nun in eine der obigen Gleichungen ein, z.B. in , und löse nach auf.
↓ Setze ein.
Gib die Lösungsmenge an. .
Hast du eine Frage oder Feedback?
Versuche die Lösung für diese nicht-linearen Gleichungen mithilfe der Verfahren zu lösen, die du schon bei linearen Gleichungssystemen kennst.
wobei
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Lineare Gleichungssysteme kannst du mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren lösen.
Probiere diese Verfahren für dieses nicht-lineare Gleichungssystem aus.
Hier eignet sich das Additionsverfahren. Wenn man die beiden Gleichungen so umformt, dass die Terme mit oder identisch sind, kann man die beiden umgeformten Gleichungen voneinander abziehen und muss nur noch eine Gleichung mit einer Variablen lösen.
Lösung mithilfe des Additionsverfahren
Mit dem Additionsverfahren kommst du auf diese Lösung:
Gegeben:
Forme so um, dass auf einer Seite alle Variablen und auf der anderen nur Zahlen sind.
Das neue Gleichungssystem lautet nun:
Die Gleichung enthält den Term und die Gleichung ein Vielfaches von und zwar . Nimm also mal und addiere dann die Gleichungen, um den Term zu eliminieren.
:
Setze nun in eine der obigen Gleichungen ein, z.B. in , und löse nach auf.
↓ Setze ein.
↓ Bilde Kehrbrüche.
Gib die Lösungsmenge an.
Hast du eine Frage oder Feedback?
Versuche die Lösung für diese nicht-linearen Gleichungen mithilfe der Verfahren zu lösen, die du schon bei linearen Gleichungssystemen kennst.
wobei und
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Lineare Gleichungssysteme kannst du mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren lösen.
Das gegebene nicht-lineare Gleichungssystem kannst du jedoch in ein lineares Gleichungssystem umwandeln.
Gegeben:
Forme und so um, dass beide Gleichungen keinen Bruch mehr beinhalten.
↓ Multipliziere mit den Nennern.
↓ Multipliziere mit den Nennern.
Das lineare Gleichungssystem lautet also:
Nun kannst du die bekannten Verfahren für die Lösung des Gleichungssystems anwenden.
Lösung mithilfe des Einsetzungsverfahren
Mit dem Einsetzungsverfahren kommst du auf diese Lösung:
Gegeben:
Forme so um, dass nur noch auf einer Seite steht.
Setze in ein.
↓ Setze ein.
↓ Löse nun nach auf.
Setze in ein, um zu berechnen.
↓ Setze ein.
Gib die Lösungmenge an.
Zusatz: Überprüfe deine Lösung durch eine Probe
Setze und in deine Gleichungen und ein und prüfe, ob die Gleichung stimmt.
↓ Setze und ein.
↓ Setze und ein.
Beide Gleichungen sind richtig, also stimmt unsere Lösung.
Hast du eine Frage oder Feedback?
Versuche die Lösung für diese nicht-linearen Gleichungen mithilfe der Verfahren zu lösen, die du schon bei linearen Gleichungssystemen kennst.
wobei und
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineares Gleichungssystem
Lineare Gleichungssysteme kannst du mit dem Einsetzungsverfahren, Gleichsetzungsverfahren oder Additionsverfahren lösen.
Probiere diese Verfahren für dieses nicht-lineare Gleichungssystem aus.
Hier eignet sich das Additionsverfahren. Wenn man die beiden Gleichungen so umformt, dass die Terme mit oder identisch sind, kann man die beiden umgeformten Gleichungen voneinander abziehen und muss nur noch eine Gleichung mit einer Variablen lösen.
Lösung mithilfe des Additionsverfahren
Mit dem Additionsverfahren kommst du auf diese Lösung:
Gegeben:
Die Gleichung enthält den Term und die Gleichung ein Vielfaches von und zwar . Nimm also mal und addiere dann die Gleichungen, um den Term zu eliminieren.
Das neue Gleichungssystem lautet also:
:
Löse nun die durch die Addition entstandene Gleichung nach auf.
↓ Bilde die Kehrbrüche.
Setze nun in eine der obigen Gleichungen ein, z.B. in , und löse nach auf.
↓ Setze ein.
↓ Bilde den Kehrbruch.
Gib die Lösungsmenge an, dabei zuerst die Lösung für , dann für .
Hast du eine Frage oder Feedback?
Versuche die Lösung für diese nicht-linearen Gleichungen mithilfe der Verfahren zu lösen, die du schon bei linearen Gleichungssystemen kennst.
- 14
Einem Schüler sind beim Lösen der folgenden Aufgaben einige Fehler unterlaufen. Korrigiere seine Lösungen.
Korrigiere die Lösung mithilfe des Gleichsetzungsverfahren
↓ Gleichsetzen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Der Fehler liegt bei dem Auflösen von , das alleine stehen muss, weshalb man durch 2 teilt
↓ Teile Gleichung I durch 2, damit alleine steht
Nun kannst du das Gleichsetzungsverfahren durchführen
Setze Gleichung I und II gleich
↓ ↓ Bring das x2 auf die andere Seite, um alle Vorkommen auf einer Seite zu haben
↓ Subtrahiere auf beiden Seiten 5
↓ Teile durch 0,5
Setze nun in Gleichung I ein.
L={(2/-2)}
Hast du eine Frage oder Feedback?
Korrigiere die folgende Lösung mithilfe des Einsetzungsverfahren
↓ Einsetzen
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Der Fehler hierbei ist, dass beim Einsetzen nicht in Klammern gesetzt wurde und somit falsch multipliziert wurde.
Setze die rechte Seite der Gleichung II vor dem Einsetzen unbedingt in eine Klammer. Ersetze in Gleichung I durch den rechten Teil von Gleichung II.
↓ ↓ Multipliziere alle Werte in der Klammer mit 3
↓ Vereinfache die Gleichung I
↓ Subtrahiere von beiden Seiten 9
↓ Teile beide Seiten durch -2
↓ Setze in Gleichung II ein
Setze in Gleichung II ein.
↓ Berechne den Term unter Beachtung von Punkt vor Strich
L={(2|0,5)}
Hast du eine Frage oder Feedback?
Korrigiere folgende Lösung mithilfe des Additionsverfahren
L = {(2/4)}
Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionsverfahren
Der Fehler hierbei ist, dass in der Regel mit addieren eine Variable wegfallen soll, was hier aber nicht funktioniert. Man muss subtrahieren.
I. - II.
↓ Nun kannst du = -3 in Gleichung I einsetzen
L = {(1/-3)}
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
