2021
Die Aufgaben findest du hier zum Ausdrucken als PDF.
- 1
Berechne
- 2
Berechne den Wert der Determinante
- 3
Die Zahl 870000 soll mit einer Zehnerpotenz dargestellt werden. Kreuze die entsprechende Darstellung der Zahl an.
- 4
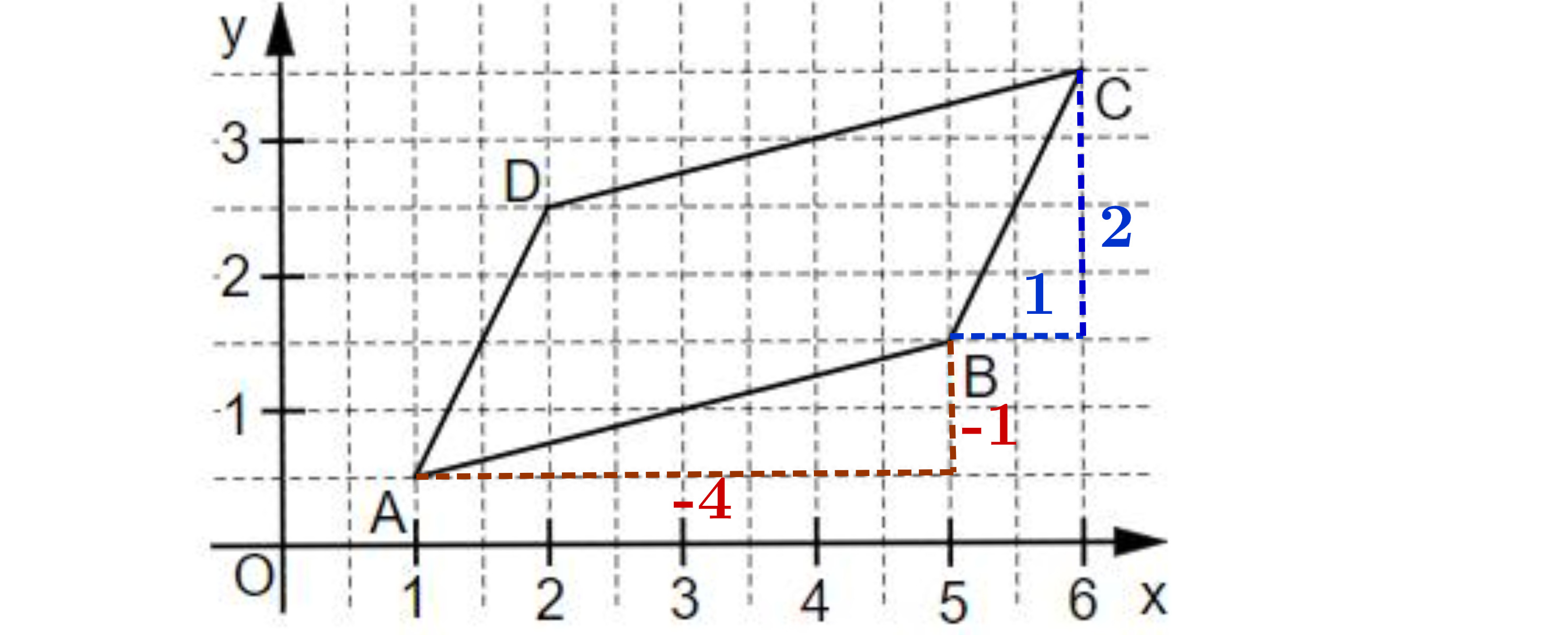
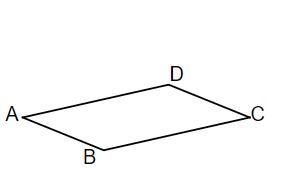
Für das Viereck ABCD gilt:
,
Begründe, wie man anhand der Pfeilkoordinaten erkennen kann, dass es sich bei dem Viereck ABCD um ein Parallelogramm handelt.
- 5
Gib die Lösungsmenge L der Gleichung an:
, (G = }
L = { _______ }
- 6
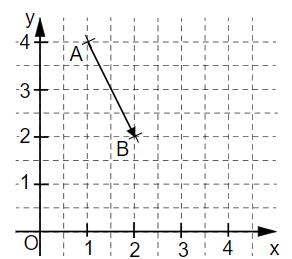
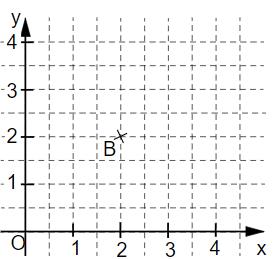
Zeichne den Pfeil in das Koordinatensystem ein.
- 7
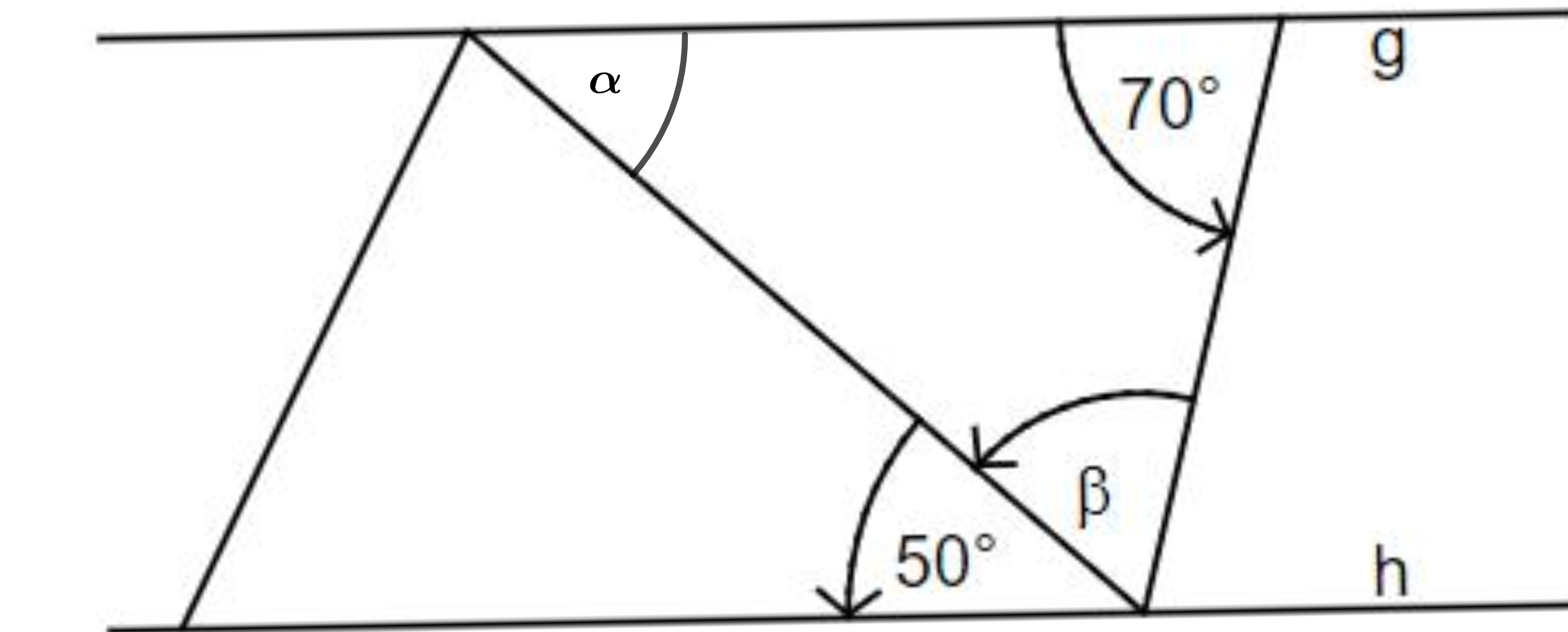
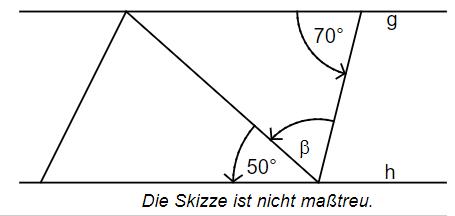
Gib das Winkelmaß β an. Es gilt: g || h.
 °
° - 8
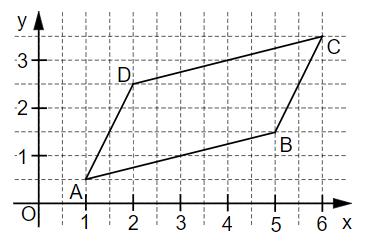
Es soll der Flächeninhalt A des Parallelogramms ABCD (siehe Abbildung) berechnet werden. Ergänze die Lücken in der Determinante.
FE
- 9
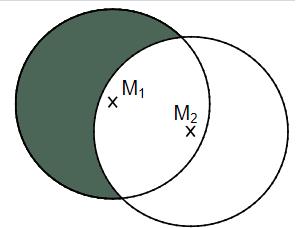
Gegeben sind zwei Kreise mit den Mittelpunkten und . Beide Kreise haben einen Radius von 4 LE. Markiere alle Punkte, die weniger als 4 LE von und zugleich mehr als 4 LE von entfernt sind.
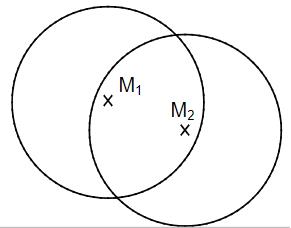
- 10
Bei der Parallelverschiebung der Figur mit dem Vektor sind Fehler unterlaufen (siehe Abbildung). Gib eine Treueeigenschaft der Parallelverschiebung an, die nicht mehr zutrifft.
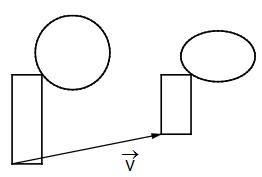
- 11
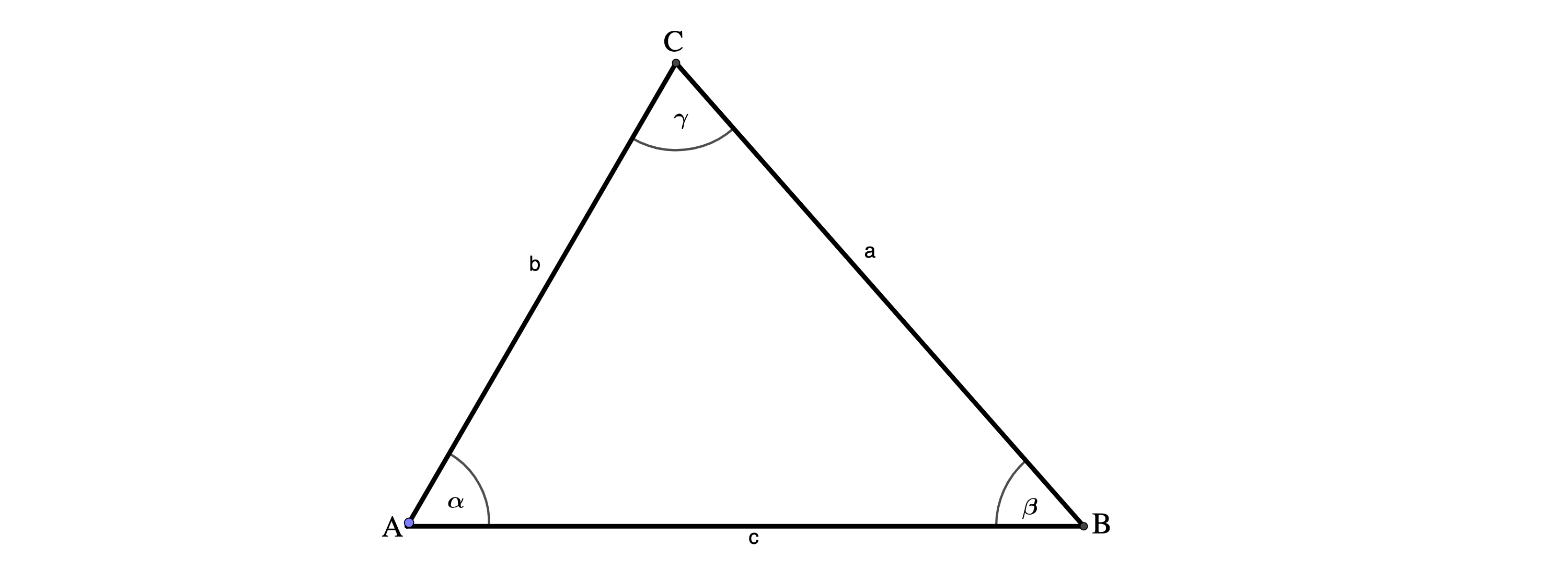
Zeichne das Dreieck ABC mit den Maßen c = 4 cm, β = 50° und γ = 70°.
- 12
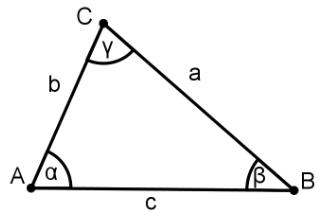
Begründe, dass es ein Dreieck ABC mit den folgenden Maßen nicht geben kann:
a = 7,5 cm; b = 3 cm; c = 5 cm; α = 40°; β = 60°; γ = 80°.
- 13
Für zwei Dreiecke sind folgende Größen bekannt:
Dreieck : cm; cm; °;
Dreieck : cm; cm; °.
Nach welchem Kongruenzsatz sind die beiden Dreiecke kongruent? Kreuze an.
- 14
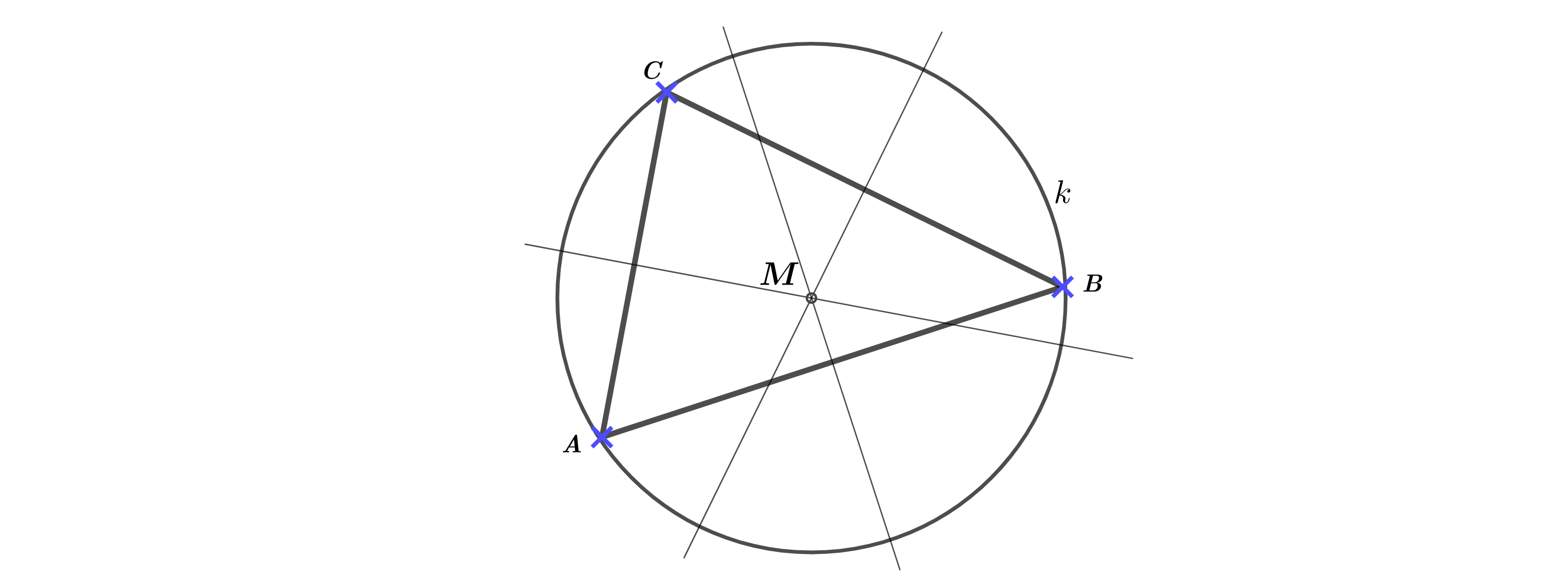
Ermittle den Mittelpunkt M des Kreises k mithilfe des Dreiecks ABC.
Es gilt: A, B, C ∈ k.
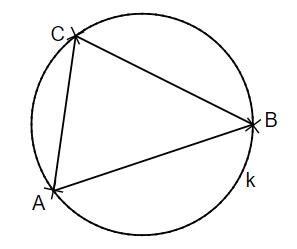
- 15
Gib zu der unten dargestellten Wertetabelle einen möglichen Term an (G = ).

T(x)=________
- 16
Welche Ungleichung passt zum Text ()?
Kreuze an. „Die Summe aus –4 und 12 ist mindestens so groß wie das Dreifache einer ganzen Zahl.“
- 17
In einem Laden wirbt der Besitzer: „Wir bieten Ihnen 20% Rabatt auf alles“. Im Schaufenster hängt eine Jeans mit einem bereits reduzierten Preis von 48 €. Berechne den ursprünglichen Preis der Hose.
€ - 18
Kreuze den Graphen an, der eine indirekte Proportionalität darstellt.
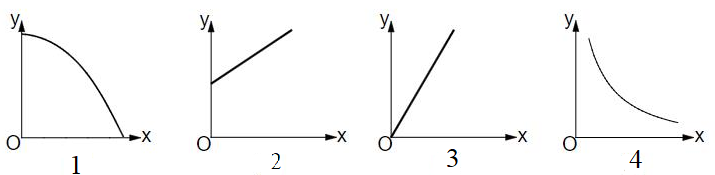
- 19
Die Grundfläche des Quaders ABCDEFGH liegt in der Ebene, die durch die Punkte A, B und C festgelegt wird. Gib drei Punkte an, die in einer Ebene liegen, die senkrecht auf der Grundfläche steht und die die Strecke beinhaltet.
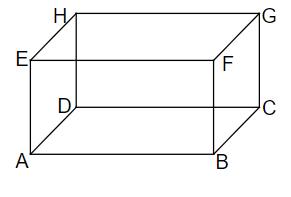
- 20
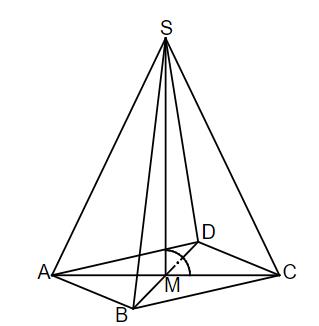
Für das Schrägbild der Pyramide ABCDS wurde bereits die Grundfläche ABCD gezeichnet. Vervollständige das Schrägbild der Pyramide ABCDS mit der Höhe , wobei M der Diagonalenschnittpunkt der Grundfläche ist.
Es gilt: = 5 cm.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?