Prüfungsaufgaben Mathematik 2025

🎓 Prüfungsbereich für Berlin

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Basisaufgaben
1. Auf ein T-Shirt gibt es $6 €$ Rabatt. Das sind $20 %$ des alten Preises. Geben Sie den alten Preis des T-Shirts an.
  
  _______ €
  [1 Pkt]
2. Geben Sie $1,5 h$ in Minuten an.
  ________ min
  [1 Pkt]
3. Kennzeichnen Sie in dem abgebildeten Quadrat ein Viertel der Fläche.
  [1 Pkt]
4. Geben Sie den Exponenten der Zehnerpotenz so an, dass die Gleichung stimmt.
  $850 000 = 8,5 \cdot 10^{\dots \dots}$
  [1 Pkt]
5. Bestimmen Sie den Anteil der grau markierten Fläche in Prozent.
  [2 Pkte]
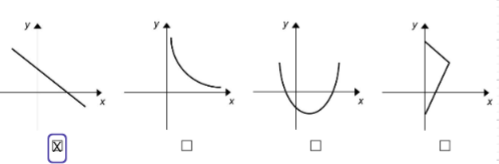
6. Kreuzen Sie die Abbildung mit dem Graphen einer linearen Funktion an.
  [1 Pkt]
7. Ergänzen Sie die Gleichung passend zur Abbildung.
  $\sin γ =_____$
  [1 Pkt]
8. Einer der unten stehenden Werte für $x$ erfüllt die Gleichung $x (x + 5) = - 6$ .
  $x = 2$
  $x = 3$
  $x = - 2$
  $x = - 6$
9. In der Abbildung ist ein Rechteck dargestellt.
  Kreuzen Sie die Gleichung an, mit der man den Flächeninhalt des gesamten Rechtecks berechnen kann.
  $A = 2 \cdot (a + b + c)$
  $A = a + 2 \cdot a \cdot b$
  $A = a \cdot (b + c)$
  $A = a \cdot b \cdot c$
2
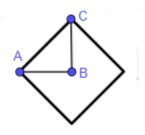
Drachenviereck
Die Diagonalen des abgebildeten Drachenvierecks haben die Maße:
$| A C | = 50 cm$
$| B D | = 80 cm$
1. Kreuzen Sie an, wie viele Symmetrieachsen das Drachenviereck hat.
  Bestätigen Sie rechnerisch, dass die Strecke $B F$ eine Länge von 55 cm hat.
  Berechnen Sie die Länge der Strecke $A B$ .
  [4 Pkte]
2. Ermitteln Sie den Flächeninhalt des Drachenvierecks $A B C D$ .
  [2 Pkte]
3. Begründen Sie, dass $γ = 90^{\circ}$ ist.
  [2 Pkte]
3
Zahlenscheiben
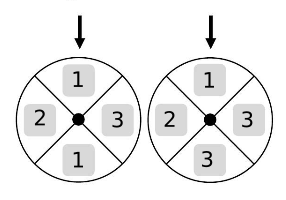
Bei einem Spiel dreht man gleichzeitig an zwei Scheiben.
Wenn sich die Scheiben nicht mehr drehen, liest man an den Pfeilen zuerst die linke und danach die rechte Ziffer ab.
Das abgebildete Beispiel zeigt die Zahl $12$ .
1. Notieren Sie alle möglichen Zahlen, die beim Drehen entstehen können.
  [1 Pkt]
2. Berechnen Sie die Wahrscheinlichkeit dafür, dass eine 33 gedreht wird.
  Esra behauptet: „Die Wahrscheinlichkeit, eine 22 zu drehen, ist genauso hoch wie die Wahrscheinlichkeit, eine 33 zu drehen."
  Entscheiden Sie, ob die Behauptung von Esra wahr ist.
  Begründen Sie Ihre Entscheidung.
  [3 Pkte]
3. Bestimmen Sie die Wahrscheinlichkeit, eine $12$ oder $21$ zu drehen.
  [2 Pkte]
4. Tragen Sie in die beiden Scheiben Ziffern so ein, dass die Wahrscheinlichkeit, eine 13 zu drehen, bei $25 %$ liegt.
  Begründen Sie Ihre Einträge durch eine Rechnung.
  [2 Pkte]
4
Rampe
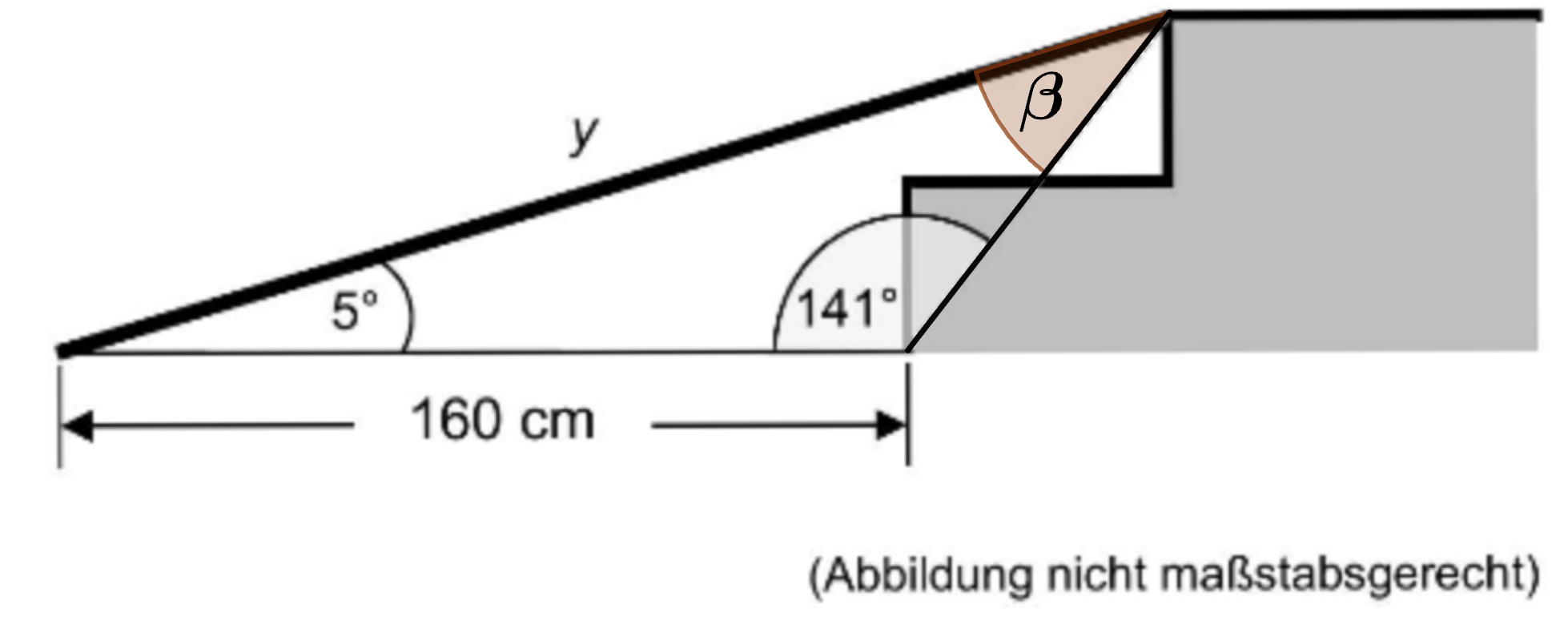
Familie Yücel möchte ihr Haus auch für Personen im Rollstuhl zugänglich machen.
An die Stufe der Eingangstür soll eine feste Rampe gebaut werden.
1. Berechnen Sie die Länge $x$ der Rampe.
  Berechnen Sie die Größe des Anstiegswinkels $α$ .
  [4 Pkte]
2. Damit eine Person im Rollstuhl eine Rampe ohne Hilfe hochfahren kann, darf die Steigung einer Rampe maximal $6 %$ betragen.
  Vervollständigen Sie den folgenden Satz:
  Eine Steigung von $6 %$ bedeutet, dass auf einer waagerechten Strecke von _____ Metern ein Höhenunterschied von _____ Metern erreicht wird.
  Frau Yücel behauptet: „Unsere Rampe wird zu steil, da die Steigung mehr als $6 %$ beträgt."
  Hat Frau Yücel Recht? Überprüfen Sie die Aussage.
  [3 Pkte]
3. Für die Treppe am Hinterausgang müssen zwei Stufen überwunden werden. Dafür wird eine mobile Rampe an die Treppe angelegt.
  Berechnen Sie die Länge $y$ der Rampe.
  [3 Pkte]
5
Funktionen
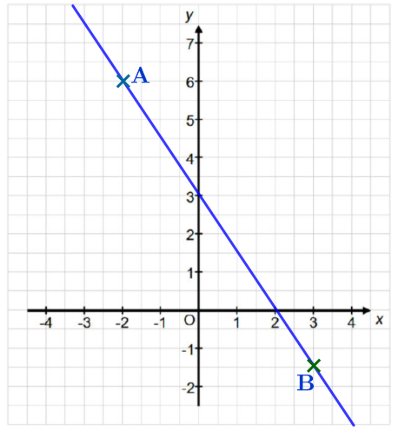
1. Der Graph einer linearen Funktion $f$ verläuft durch die Punkte $A (- 2 | 6)$ und $B (3 | - 1,5)$ .
  Zeichnen Sie den Graphen $f$ von in das abgebildete Koordinatensystem ein. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.
  Kreuzen Sie an.
  Geben Sie eine Gleichung der Funktion $f$ an.
  [4 Pkte]
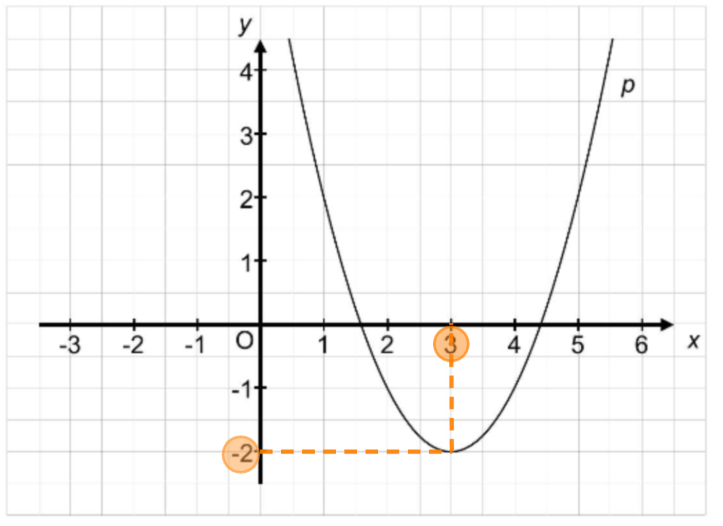
2. Gegeben ist die quadratische Funktion $p$ mit $p (x) = x^{2} - 6 x + 7$ .
  Die Abbildung zeigt die Parabel p.
  Geben Sie die Koordinaten des Scheitelpunktes $S$ von $p$ an.
  $S (|) |$
  Geben Sie eine Gleichung der Funktion $p$ in Scheitelpunktform an.
  $p (x) =$
  [2 Pkte]
3. Berechnen Sie die Koordinaten der Schnittpunkte der Parabel $p$ mit der $x$ -Achse.
  [4 Pkte]
6
Kita
1. In einer Kita wurde das Alter der Kinder und der Erziehenden erfasst.
  Die folgende Liste zeigt das Alter der Kinder einer Gruppe:
  Kreuzen Sie die falsche Aussage an und korrigieren Sie diese.
  [2 Pkte]
2. Die folgende Liste zeigt das Alter der 11 Erziehenden in der Kita:
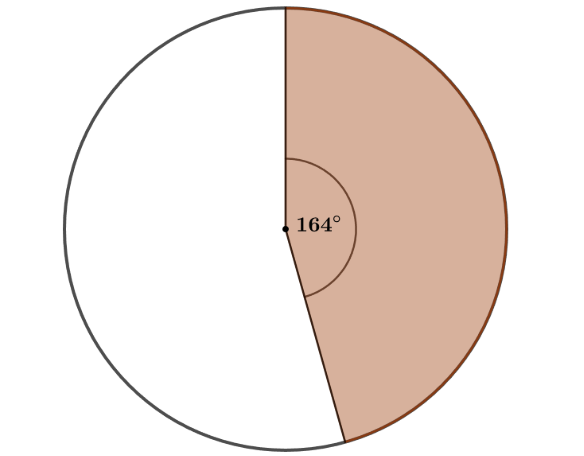
  Ermitteln Sie den prozentualen Anteil der Erziehenden, die jünger als 50 Jahre sind.
  Stellen Sie diesen prozentualen Anteil im Kreisdiagramm dar.
  [3 Pkte]
3. Bestimmen Sie das Durchschnittsalter der Erziehenden in der Kita.
  Die älteste und die jüngste Person in der Gruppe der Erziehenden verlassen die Kita.
  Erklären Sie, wie sich diese Veränderung auf das Durchschnittsalter auswirkt.
  [3 Pkte]
7
Bakterien
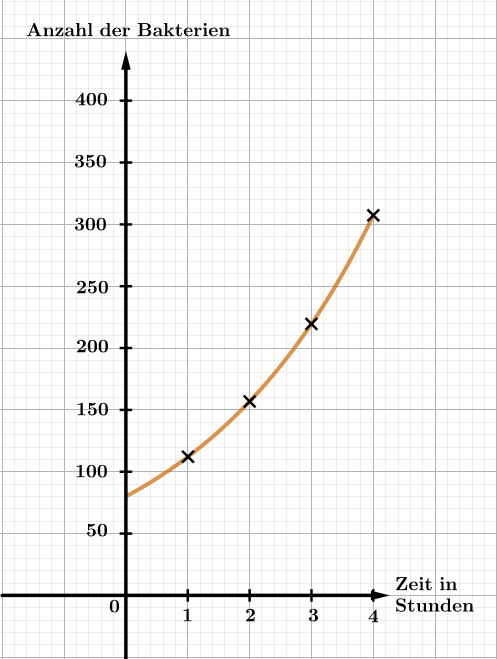
Das exponentielle Wachstum eines Bakterienstammes wird beobachtet.
1. Die Tabelle zeigt das Wachstum des Bakterienstammes in den ersten 4 Stunden.
  Stellen Sie das Bakterienwachstum im Koordinatensystem dar.
  [2 Pkte]
2. Weisen Sie nach, dass der Wachstumsfaktor 1,4 beträgt.
  Geben Sie eine Gleichung an, die das Bakterienwachstum nach $t$ Stunden beschreibt.
  Überprüfen Sie rechnerisch, ob folgende Aussage wahr ist:
  „Nach 24 Stunden ist der Bakterienstamm auf mehr als $250 000$ Bakterien angewachsen."
  [4 Pkte]

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Prüfungsaufgaben Mathematik 2025

Basisaufgaben

Drachenviereck

Zahlenscheiben

Rampe

Funktionen

Kita

Bakterien