Anwendungsaufgaben mit gebrochen rationalen Funktionen
- 1
Anwendungsbeispiele:
Zur Bestimmung der Schwerkraft y (in N) auf einen Körper der Masse 1kg in der Entfernung x von der Erdoberfläche (in km) gilt die Formel . Was erhält man für x=0? Was für sehr große x-Werte?
Ist das Anfangskapital eines Aktienbesitzers und das Endguthaben bei der Rendite ("Zinssatz") x (als Dezimalzahl, also x = 0,03 bei 3%), so berechnet man das Endguthaben mit = . Umgekehrt war also das Anfangsguthaben bzw. als Funktionsterm geschrieben z. B. bei = 15000:
Wie müssten in diesem Beispiel negative x-Werte (z.B. x=-0,8) interpretiert werden? Wie die Definitionslücke? Wie die waagrechte Asymptote?
- 2
Auf einem Streckenabschnitt soll eine Autobahnteilstrecke neu gebaut werden.
Durch Steigungen und Gefälle können Probleme für die Verkehrsteilnehmer entstehen.Deshalb werden beim Neubau von Autobahnen Steigungen über vermieden.
Das Steigungsprofil der geplanten Autobahnstrecke wird durch die Funktion beschrieben (siehe Figur 1).

Begründe rechnerisch, warum die neue Autobahnstrecke mit diesem Steigungsprofil nicht gebaut werden kann.
Im Intervall [-4;+4] soll die Autobahn daraufhin parabelförmig mit dem Höhenverlauf
untertunnelt werden (siehe Figur 2 und die Vergrößerung in Figur 3).

Kann die geplante Autobahnteilstrecke jetzt gebaut werden?
Bestätige deine Rechenergebnisse z.B. mithilfe von Geogebra graphisch.
- 3
Beim Neubau von Autobahnen werden Steigungen über 6% vermieden. Deshalb sind oft Untertunnelungen oder Geländeabtragungen nötig.
Bei dieser Aufgabe wird das Steigungsprofil der geplanten Autobahnstrecke durch die Funktion
beschrieben (siehe Fig. 1).
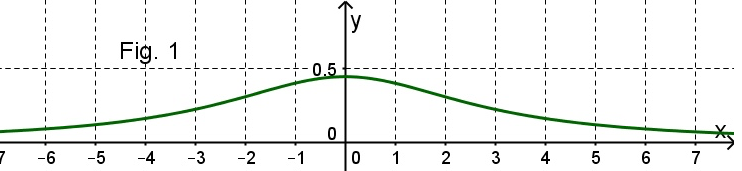
Begründe rechnerisch, warum die neue Autobahnstrecke mit diesem Steigungsprofil nicht gebaut werden kann.
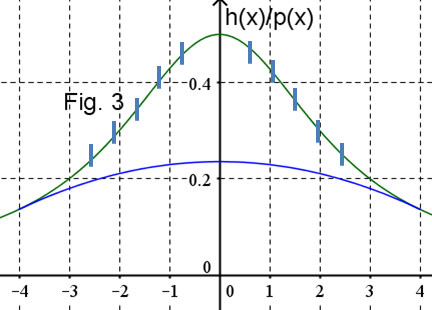
Im Intervall [-2;+2] soll das Gelände daraufhin parabelförmig mit dem Höhenprofil
abgetragen werden (siehe die Fig.2 und die Vergrößerung in Fig.3)
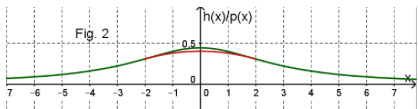
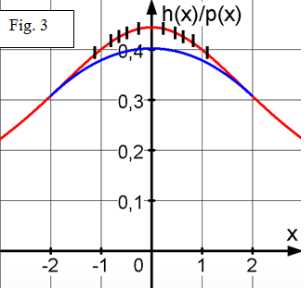
Kann die Autobahn jetzt gebaut werden?
Bestätige das Rechenergebnis graphisch, indem du z.B. in einem Geogebra-Applet die kritischen Steigungswerte überprüfst!
- 4
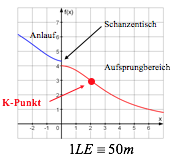
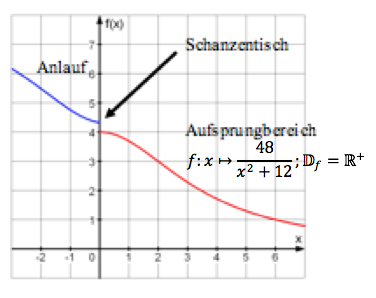
Das Aufsprungprofil einer Skisprungschanze wird näherungsweise durch folgende Funktion beschrieben:
Unter dem "K-Punkt" einer Sprungschanze versteht man den Aufsprungpunkt mit der geringsten Aufsprungbelastung für den Springer.
Berechne die horizontale Entfernung des K-Punktes vom Schanzentisch sowie den Neigungswinkel der Aufsprungbahn im K-Punkt.
Maßstab der Zeichnung:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?