Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Berechnen Sie die reellen Zahlen x und y, die das folgende Gleichungssystem erfüllen: (2 BE)
- 2
Ein Lastwagen beliefert ein Ferienhaus im Süden Europas mit Wasser. Schätzen Sie mithilfe der Abbildung ab, wie viele Kubikmeter Wasser der Wassertank des Lastwagens fasst. (2 BE)
Hinweis: Bei einer Abschätzung muss grundsätzlich der Lösungsweg nachvollziehbar sein.
- 3
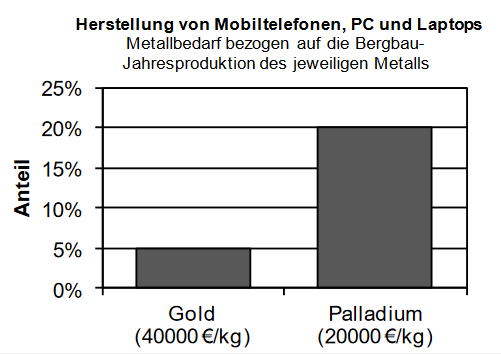
Die Abbildung zeigt für das Jahr 2010, welcher Anteil der Bergbau-Jahresproduktion von Gold bzw. Palladium für die Herstellung von Mobiltelefonen, PC und Laptops aufgewendet wurde. Außerdem ist für die beiden Edelmetalle jeweils der Wert pro Kilogramm in Euro angegeben.
Im Jahr 2010 wurden weltweit für die Herstellung von ungefähr zwei Milliarden Mobiltelefonen, PC und Laptops 40 Tonnen Palladium verwendet. Kreuzen Sie an, wie viele Tonnen Palladium im Jahr 2010 durch Bergbau gewonnen wurden. (1 BE)
Man geht davon aus, dass sich in Deutschland in den Haushalten 100 Millionen Mobiltelefone befinden, die nicht mehr verwendet werden. Durchschnittlich enthält ein Mobiltelefon 20 Milligramm Gold. Berechnen Sie den Gesamtwert (in Euro) des in diesen Mobiltelefonen enthaltenen Golds. (2 BE)
- 4
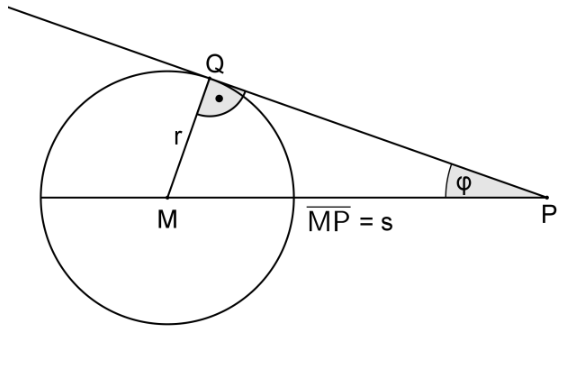
Die Abbildung zeigt einen Kreis mit dem Mittelpunkt und dem Radius . Der Punkt hat von die Entfernung . Eine durch verlaufende Tangente an den Kreis berührt diesen im Punkt .
Beschreiben Sie in Kurzform, wie man den Punkt konstruieren kann, wenn nur der Kreis mit dem Mittelpunkt sowie der Punkt gegeben sind. (2 BE)
Hinweis: In der geforderten Kurzform müsste z. B. die Konstruktion einer Parallelen nicht beschrieben werden.
Geben Sie einen Term an, mit dem aus und berechnet werden kann. (1 BE)
Durch den Punkt wird eine zweite Tangente an den Kreis gezeichnet. Sie berührt den Kreis im Punkt , der mit und die Eckpunkte eines Drachenvierecks bildet. Geben Sie einen Term an, mit dem man den Flächeninhalt dieses Drachenvierecks aus und berechnen kann. (1 BE)
Entscheiden Sie für jede der folgenden Gleichungen, ob sie richtig oder falsch ist. Kreuzen Sie nur die richtigen Gleichungen an. (2 BE)
- 5
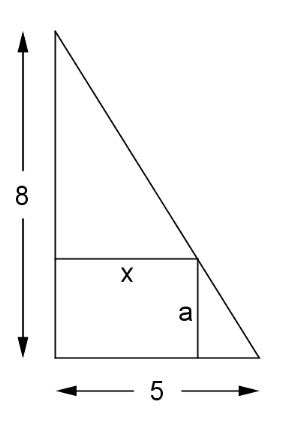
Eine von Gehwegen begrenzte Rasenfläche hat die Form eines rechtwinkligen Dreiecks, dessen Katheten acht Meter bzw. fünf Meter lang sind. Für die Rasenfläche ist ein Sandkasten in der Form eines Rechtecks vorgesehen, dessen Eckpunkte wie abgebildet auf den Seiten des Dreiecks liegen. Dieses Rechteck ist Meter lang und Meter breit.
Mithilfe des Strahlensatzes wurde eine Gleichung aufgestellt, die den Zusammenhang zwischen und richtig beschreibt. Kreuzen Sie diese Gleichung an. (1 BE)
Der Flächeninhalt des abgebildeten Rechtecks lässt sich in Abhängigkeit von durch die Funktion mit
und beschreiben. Geben Sie die Nullstellen der Funktion und mithilfe dieser Nullstellen die x-Koordinate des Scheitels der zu gehörenden Parabel an. (2 BE)
Deuten Sie im Sachzusammenhang die x-Koordinate des Scheitels der zu gehörenden Parabel. (1 BE)
- 6
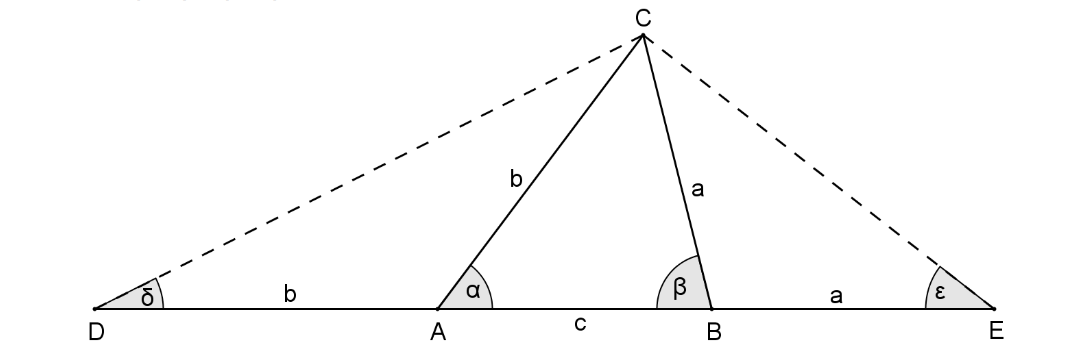
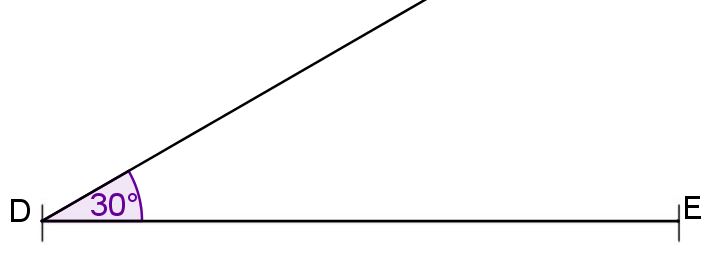
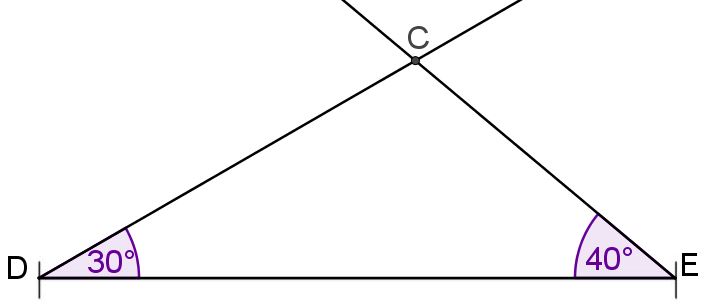
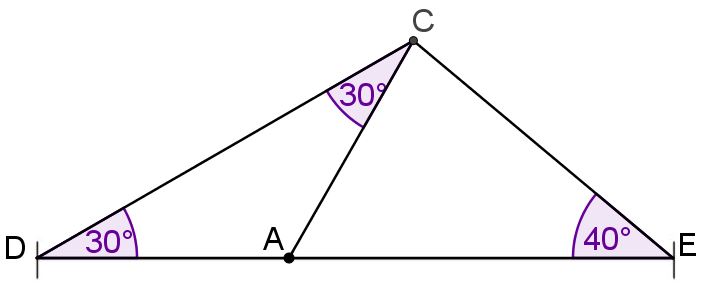
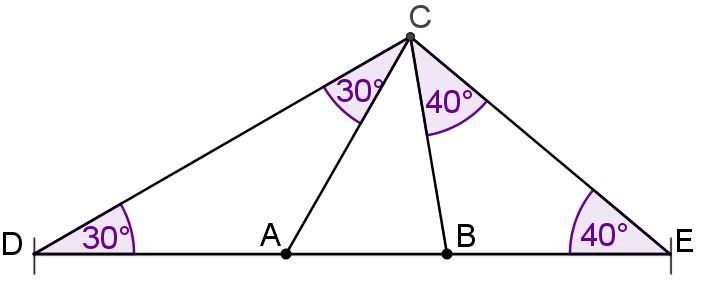
Es soll ein Dreieck ABC gezeichnet werden, für das der Umfang sowie die Winkelgrößen und gegeben sind; dazu soll die abgebildete, nicht maßstabsgetreue Überlegungsfigur genutzt werden.
Begründen Sie, dass gilt. (2 BE)
Zeichnen Sie das Dreieck , wenn sein Umfang u durch die unten gezeichnete Strecke gegeben ist. Beschriften Sie Ihre Zeichnung so, dass der Lösungsweg erkennbar wird. (2 BE)
Hinweis: Im Originaltext wurde auf dem Blatt eine Strecke für den Umfang vorgegeben.
Wenn du die Aufgabe bearbeiten möchtest, zeichne als Umfang eine etwa lange Strecke wie unten abgebildet.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?