Aufgaben zu Graphen linearer Funktionen
- 1
Zeichne den Graphen der linearen Funktionen in ein Koordinatensystem ein!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm linearer Funktionen
Zeichnen der linearen Funktion
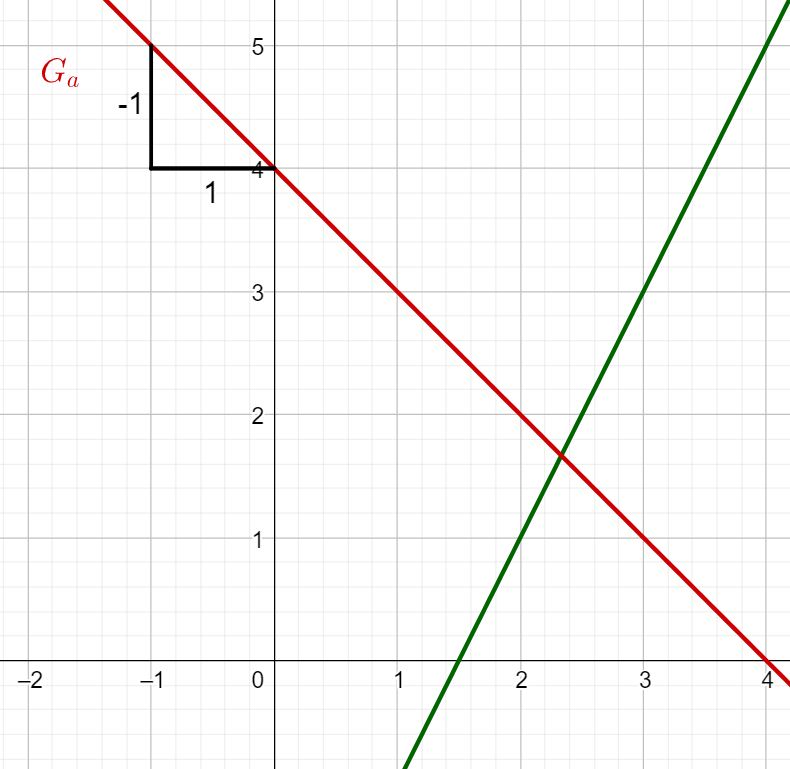
Lese zunächst -Achsenabschnitt und die Steigung aus dem Funktionsterm der linearen Funktion ab.
In diesem Fall:
Du erhältst für den -Achsenabschnitt und für die Steigung .
Zeichne zuerst den Schnittpunkt mit der -Achse ein, der sich durch den -Achsenabschnitt ergibt. Dieser lautet also .
Zeichne anschließend mithilfe der Steigung ein Steigungsdreieck. Gehe dafür eine Längeneinheit nach rechts und zwei Längeneinheiten nach unten. Dadurch erhältst du den Punkt . Ziehe nun die Gerade durch die Punkte und .
Du erhältst den Graphen von .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm der linearen Funktion
Zeichnen der linearen Funktion
Lese zunächst -Achsenabschnitt und die Steigung aus dem Funktionsterm der linearen Funktion ab.
In diesem Fall:
Du erhältst für den -Achsenabschnitt und für die Steigung .
Zeichne zuerst den Schnittpunkt mit der -Achse ein, der sich durch den -Achsenabschnitt ergibt. Dieser lautet also .
Zeichne anschließend mithilfe der Steigung ein Steigungsdreieck. Gehe dafür zwei Längeneinheiten nach rechts und eine Längeneinheit nach oben. Du erhältst den Punkt .
Zeichne die Gerade durch die Punkte und .
Du erhältst den Graphen von .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm der linearen Funktion
Zeichnen der linearen Funktion
Die Funktion stellt einen Spezialfall der linearen Funktionen dar. Die Steigung von ist gleich .
Das bedeutet, dass sich der Funktionswert unabhängig der Variable nicht ändert.
Wenn du also für jeden Wert den Funktionswert in ein Koordinatensystem einzeichnest erhältst du eine Gerade, die parallel zur -Achse auf der Höhe verläuft.
Hast du eine Frage oder Feedback?
- 2
Zeichne die Graphen der Funktionen mit folgender Funktionsgleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme die Steigung der Funktion
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Gehe von dem zuvor ermittelten Punkt eine Einheit nach rechts und 3 nach oben, da m gleich 3 ist. Hier befindet sich ein zweiter Punkt der Funktion.
Verbinde anschließend die beiden Punkte zu einer Geraden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Gleichung umstellen
Die Gleichung wird umgestellt, damit sie das Format der allgemeinen Geradengleichung hat.
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend m, nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
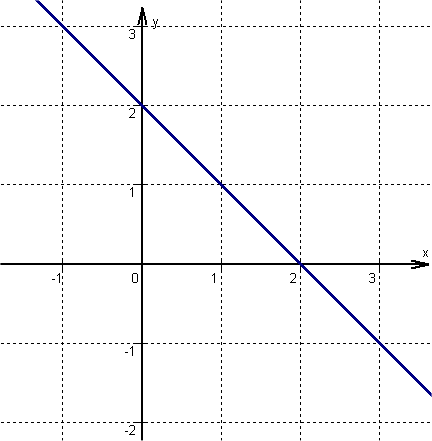
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Ein Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend , nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion.
Anschließend die beiden Punkte zu einer Geraden verbinden.
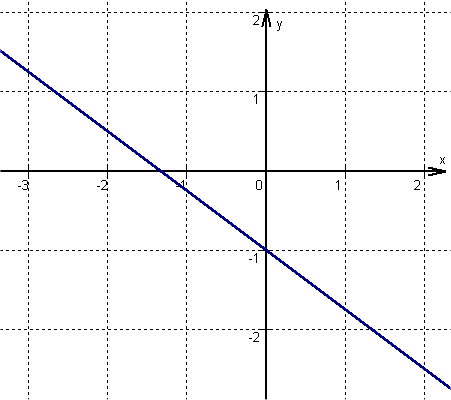
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend , nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
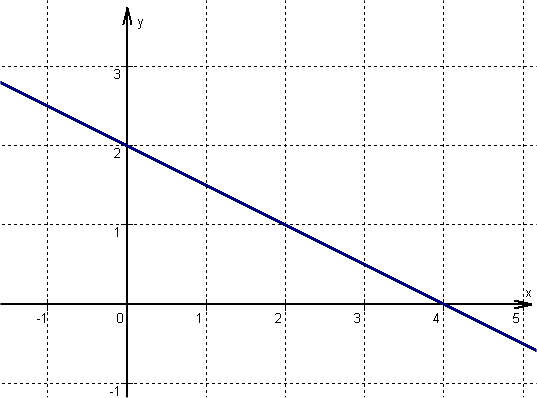
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht m der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend m, nach oben gehen, da m positiv ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
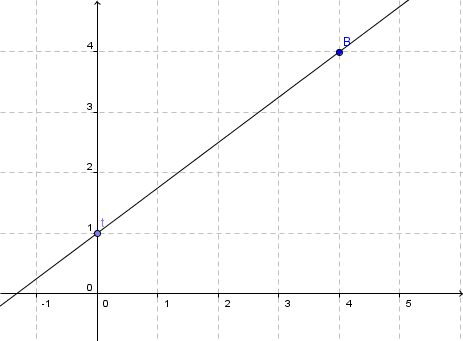
Hast du eine Frage oder Feedback?
- 3
Zeichne die Graphen folgender Geraden mit dem Schnittpunkt mit der y-Achse und dem Steigungsdreieck. Berechne den Schnittpunkt mit der x-Achse und überprüfe das Ergebnis anhand des Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
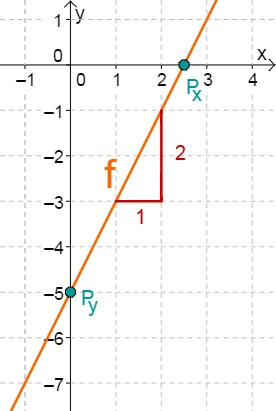
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
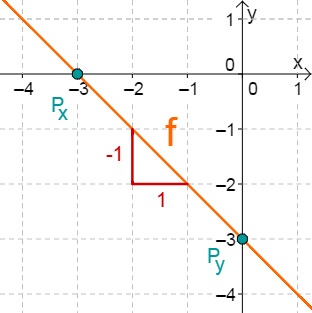
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
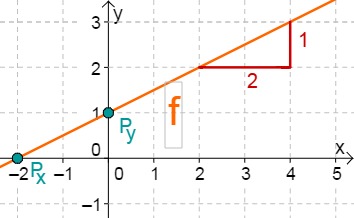
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
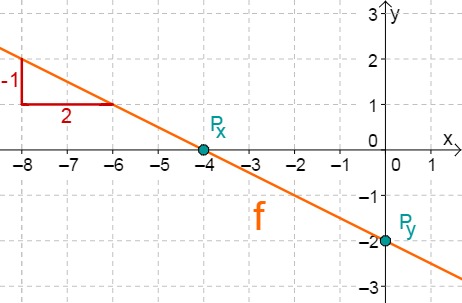
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
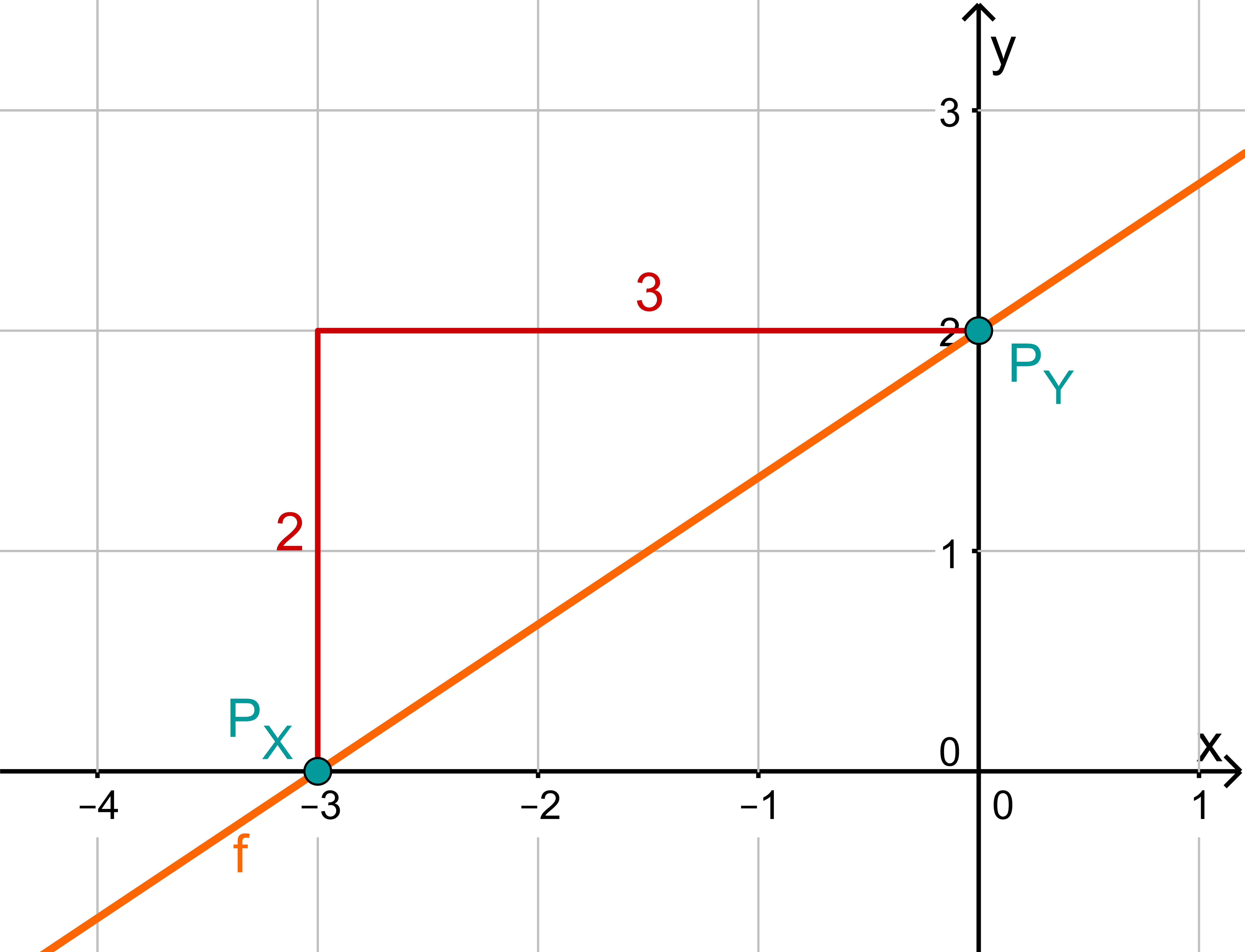
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
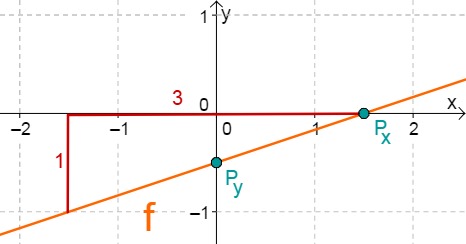
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
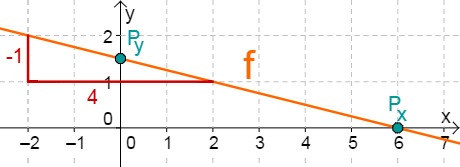
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
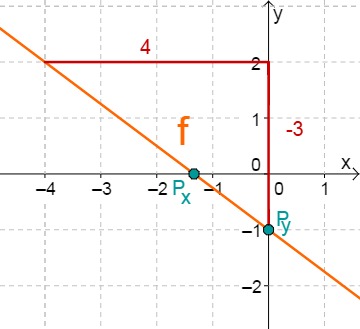
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
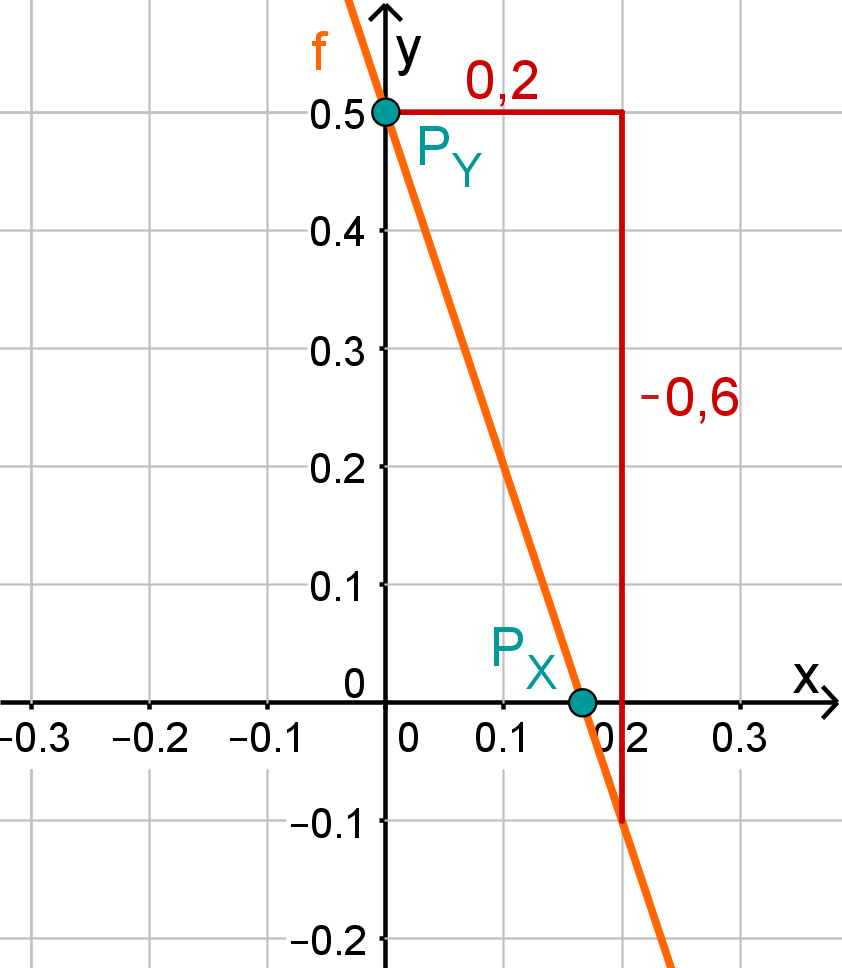
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
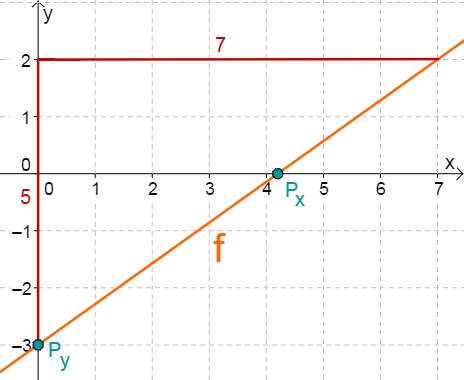
Hast du eine Frage oder Feedback?
- 4
Zeichnen Sie die Graphen folgender Funktionen jeweils in ein Koordinatensystem.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
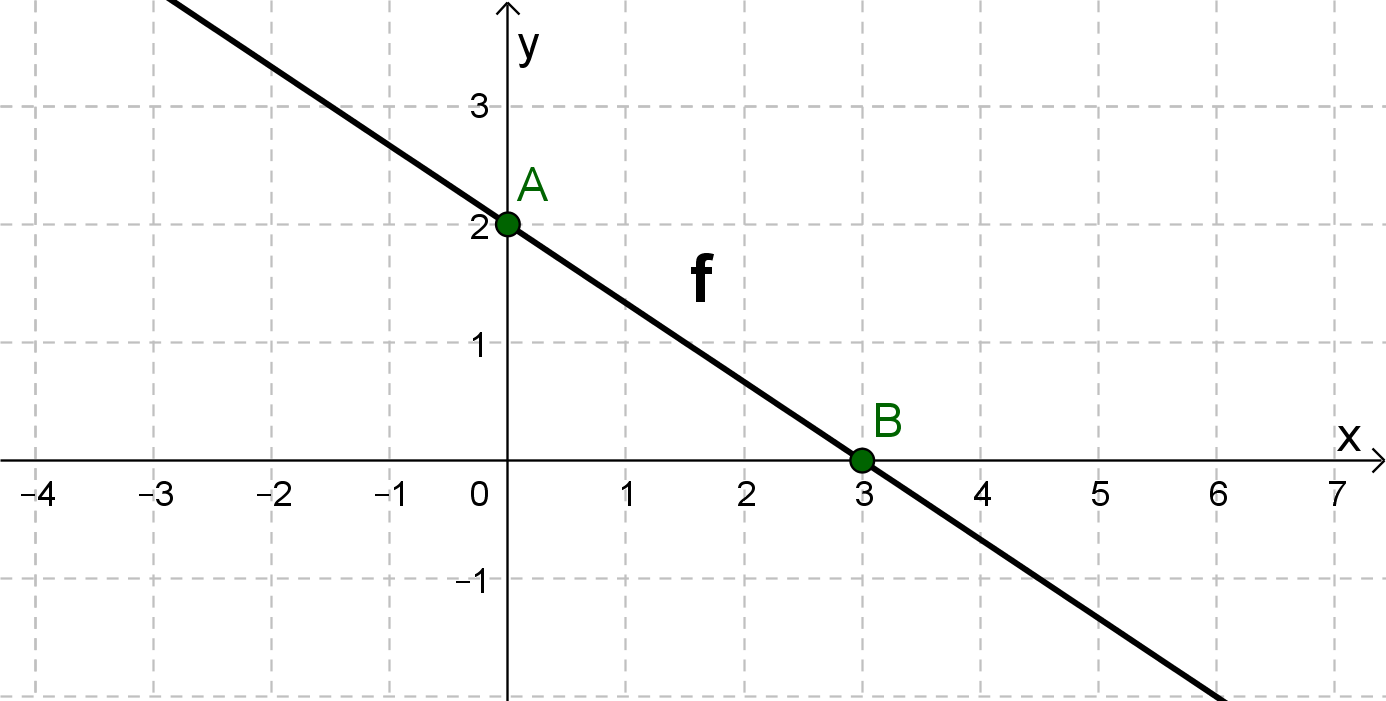
Hast du eine Frage oder Feedback?
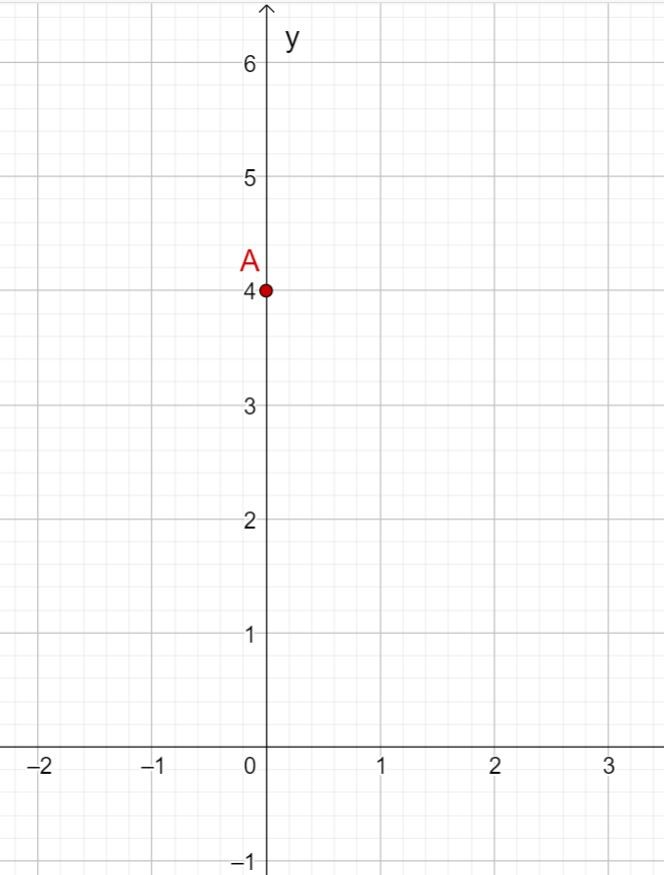
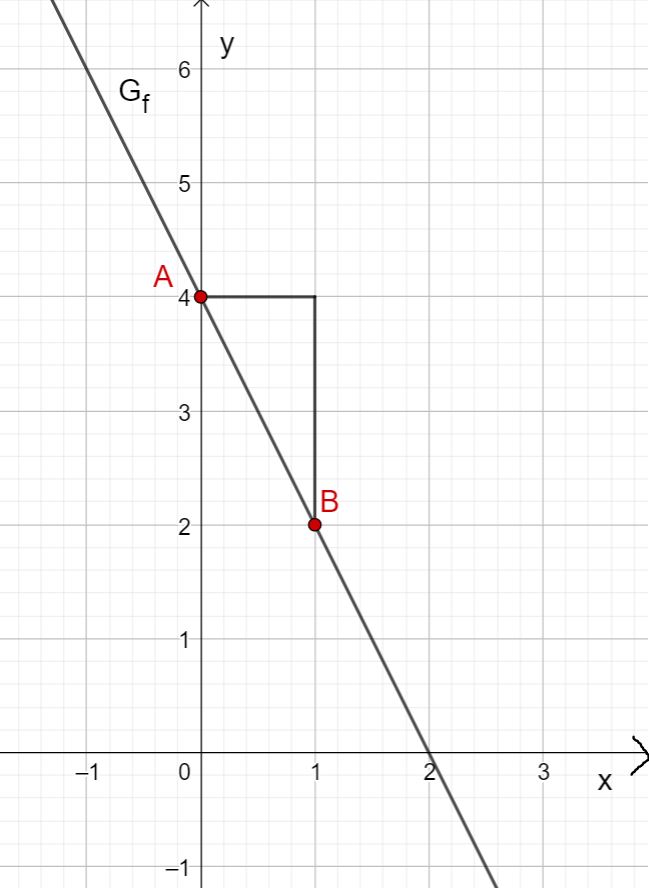
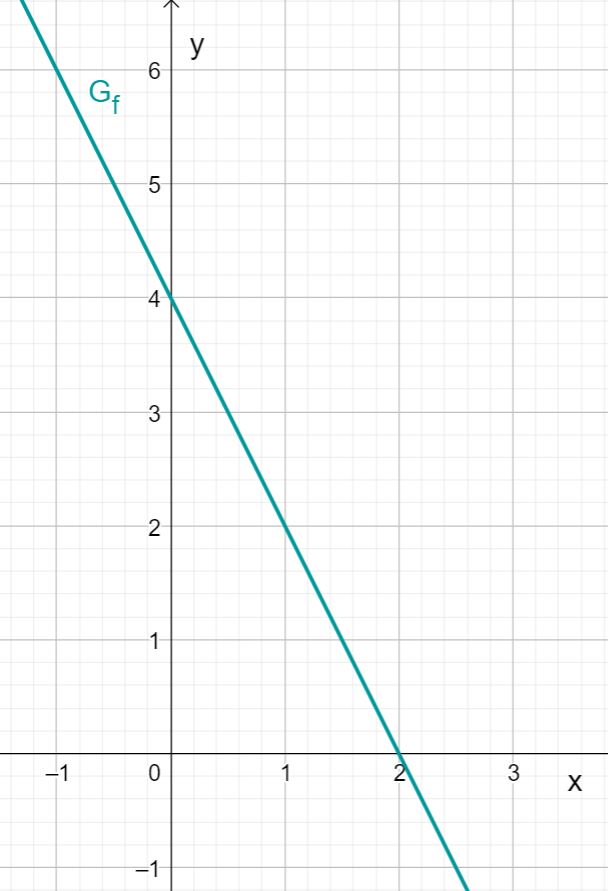
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|2)).
Gehe entsprechend der Steigung 3 nach rechts und 2 nach unten und zeichne den Punkt ein (hier B(3|0)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
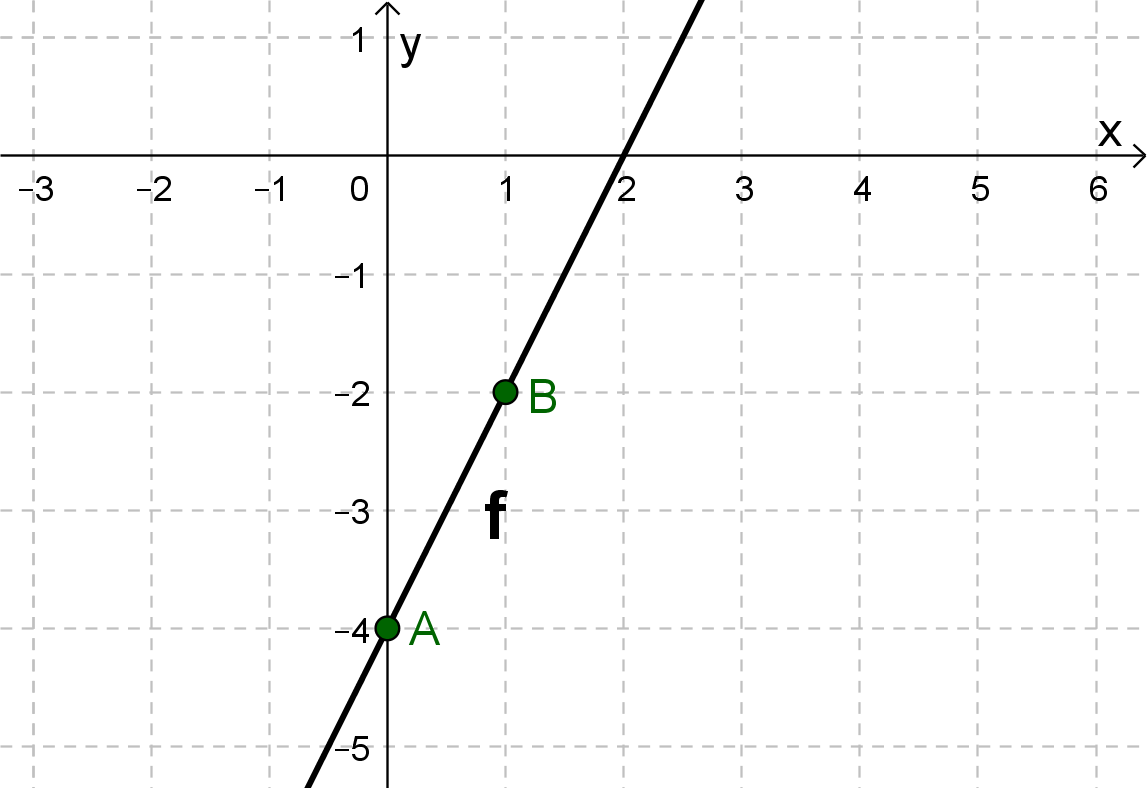
Hast du eine Frage oder Feedback?
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|-4)).
Gehe entsprechend der Steigung 1 nach rechts und 2 nach oben und zeichne den Punkt ein (hier B(1|-2)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
Hast du eine Frage oder Feedback?
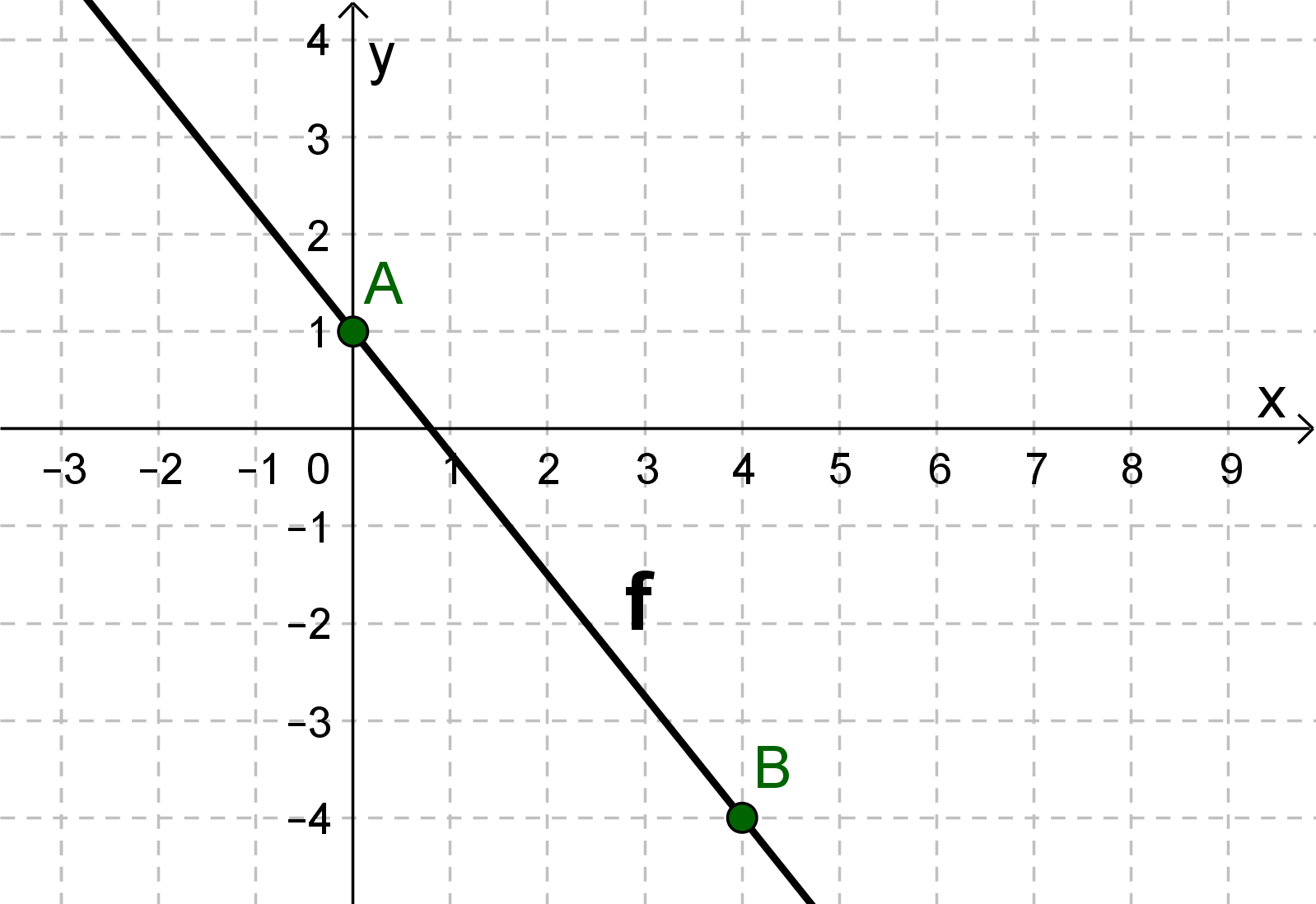
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|1)).
Gehe entsprechend der Steigung 4 nach rechts und 5 nach unten und zeichne den Punkt ein (hier B(4|-4)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
Hast du eine Frage oder Feedback?
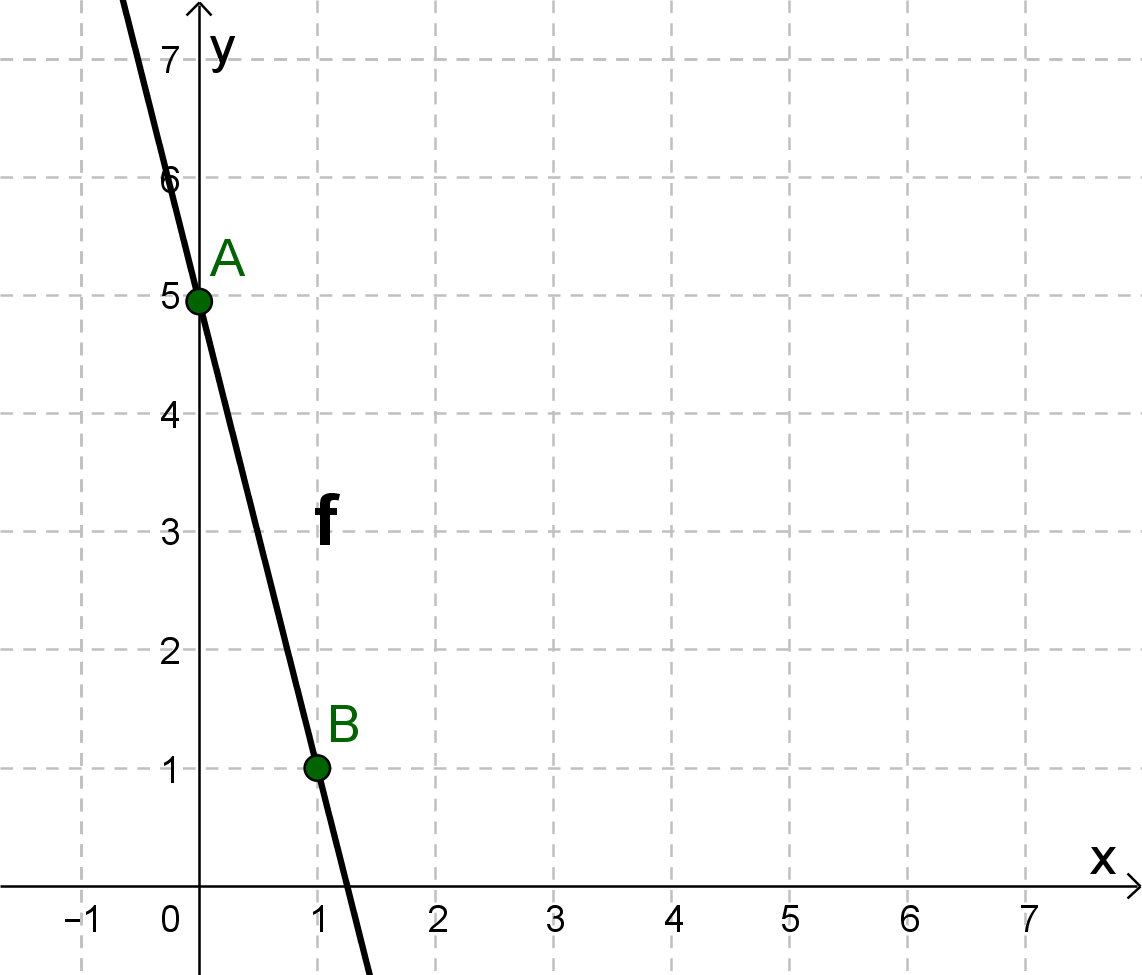
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|5)).
Gehe entsprechend der Steigung 1 nach rechts und 4 nach unten und zeichne den Punkt ein (hier B(1|1)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
Hast du eine Frage oder Feedback?
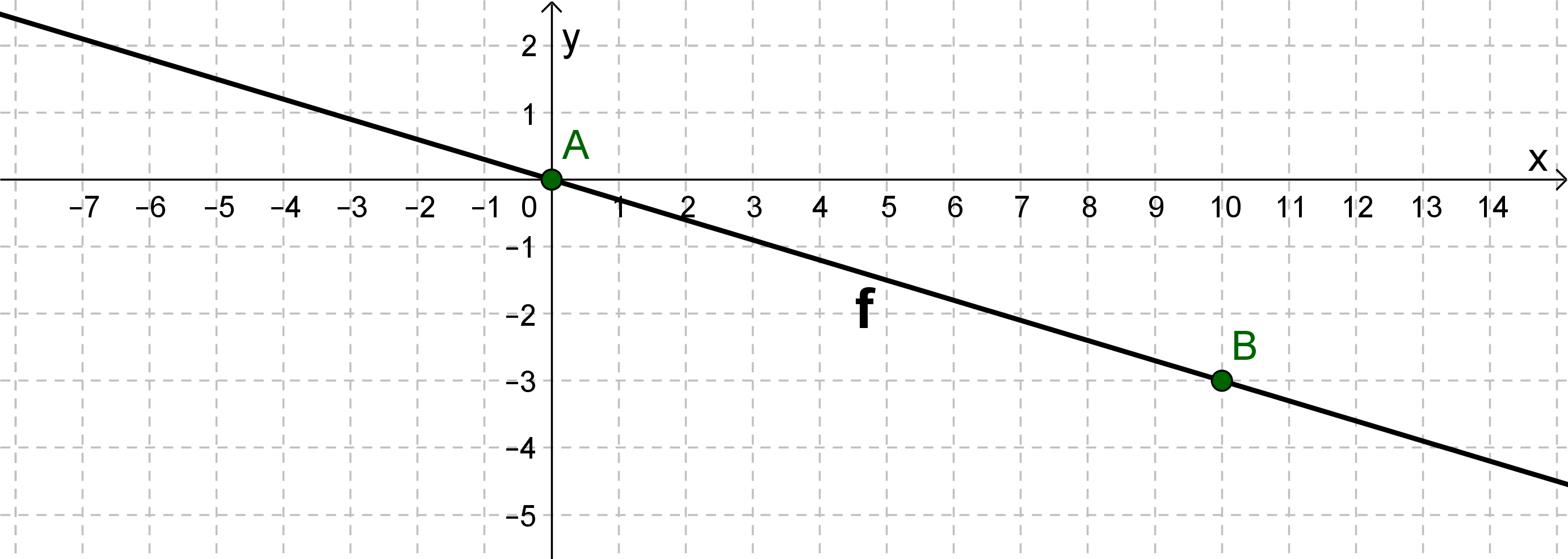
Der Vergleich mit der allgemeinen Form der Geradengleichung , ergibt: Achsenabschnitt und Steigung
Aus dem Wert des y-Achsenabschnitt folgt, dass es sich um eine Ursprungsgerade handelt. Der eine Geradenpunkt ist deshalb der Ursprung: .
Schreibe die Steigung als Bruch: . Gehe entsprechend der Steigung 10 nach rechts und 3 nach unten. Dort ist der zweiten Geradenpunkt .
Die Gerade verläuft durch die beiden Punkte und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
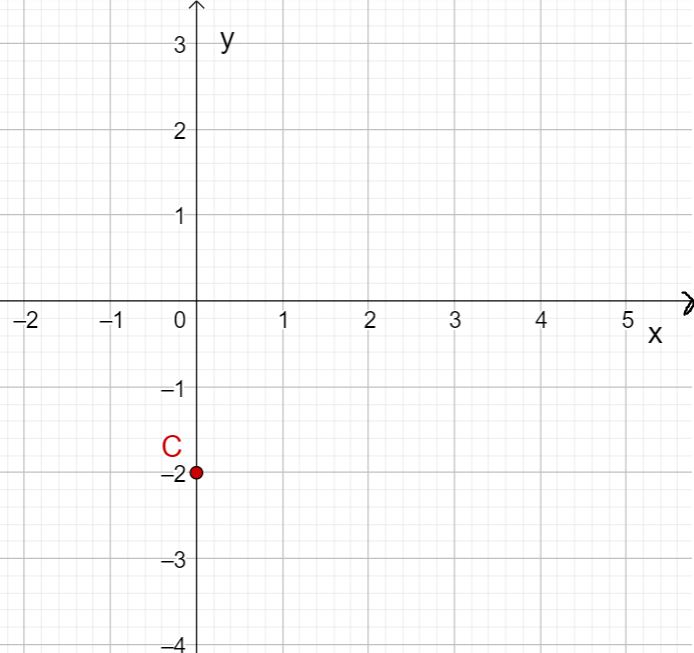
Der y-Wert der Gerade ist immer 2,5. Darum ist die Gerade eine Parallele zur x-Achse.

Hast du eine Frage oder Feedback?
- 5
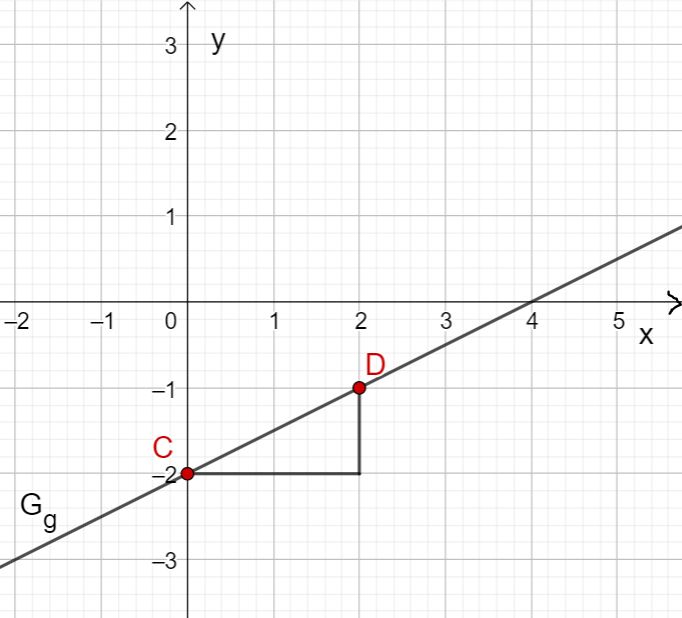
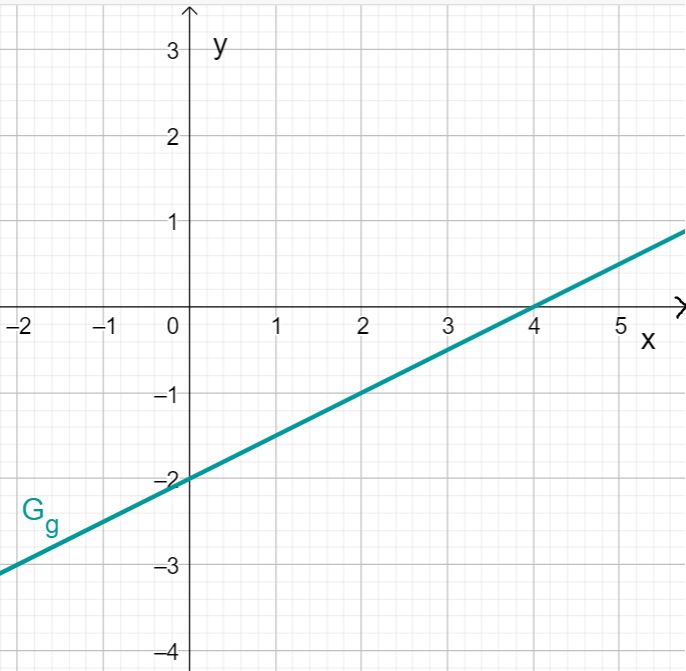
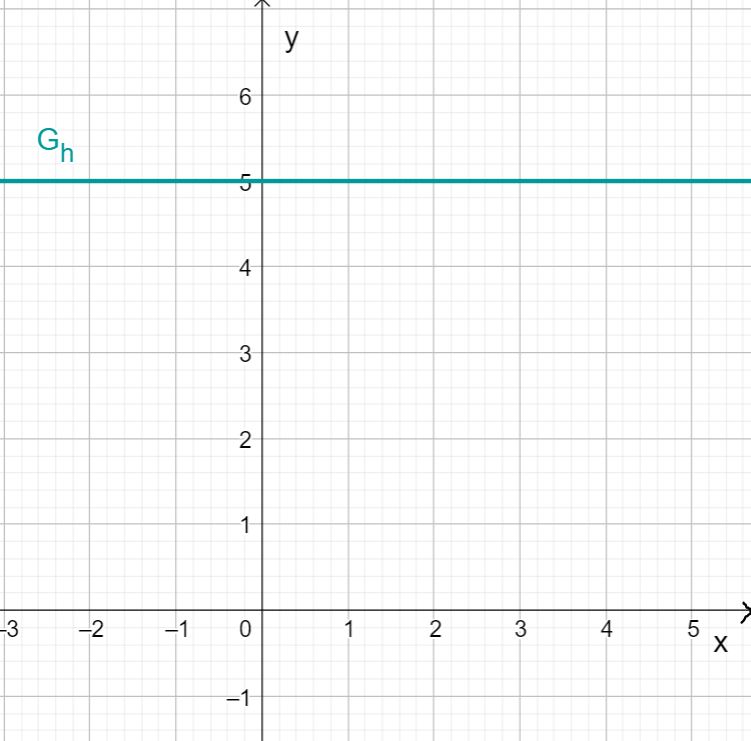
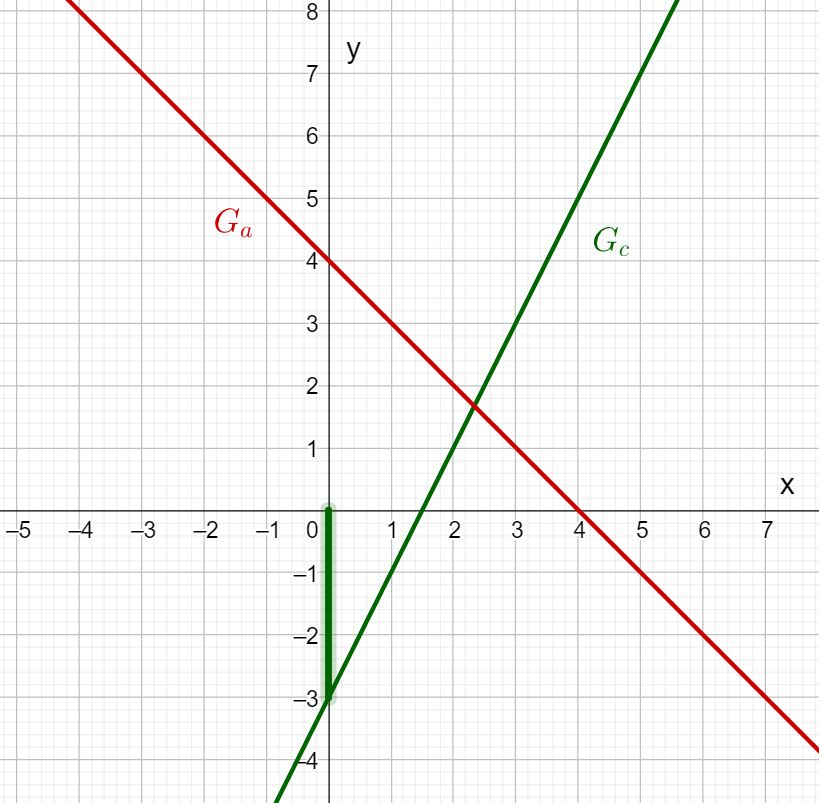
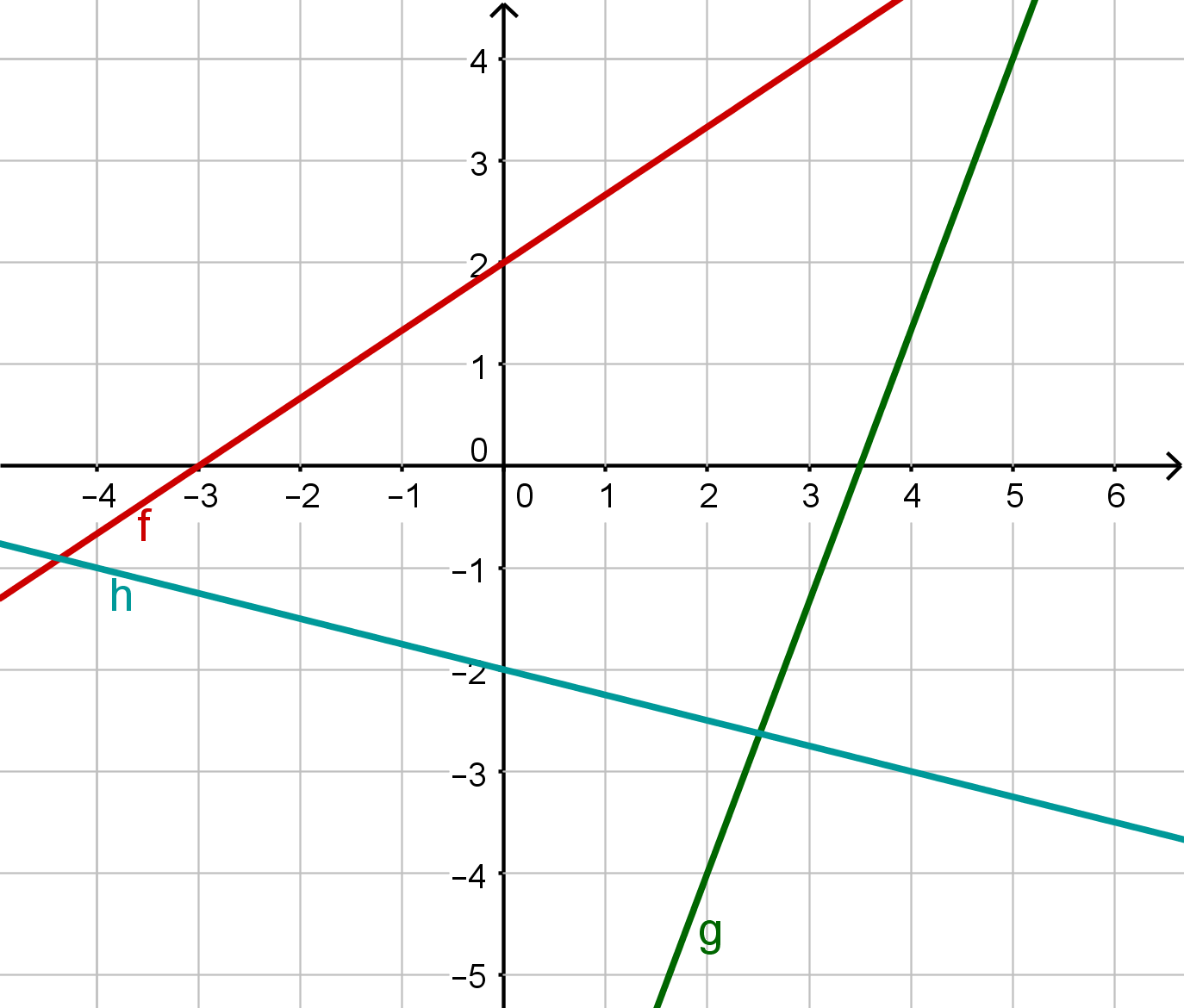
Bestimmung von Schnittpunkten
Gegeben ist eine Gerade g und eine Gerade h.
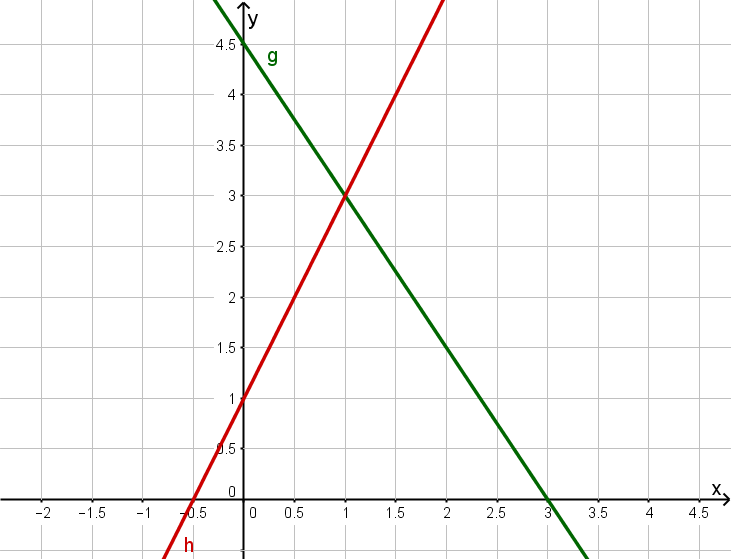
Bestimme die Geradengleichungen von g und h.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Der Parameter ist die Steigung der Geraden. Der Parameter ist der y-Achsenabschnitt.
Gerade g:
Die Gerade g hat die Steigung , das heißt .
Sie schneidet die y-Achse bei , das heißt .
Gerade h:
Die Gerade h hat die Steigung , das heißt
Die Gerade schneidet die y-Achse bei , das heißt .
Hast du eine Frage oder Feedback?
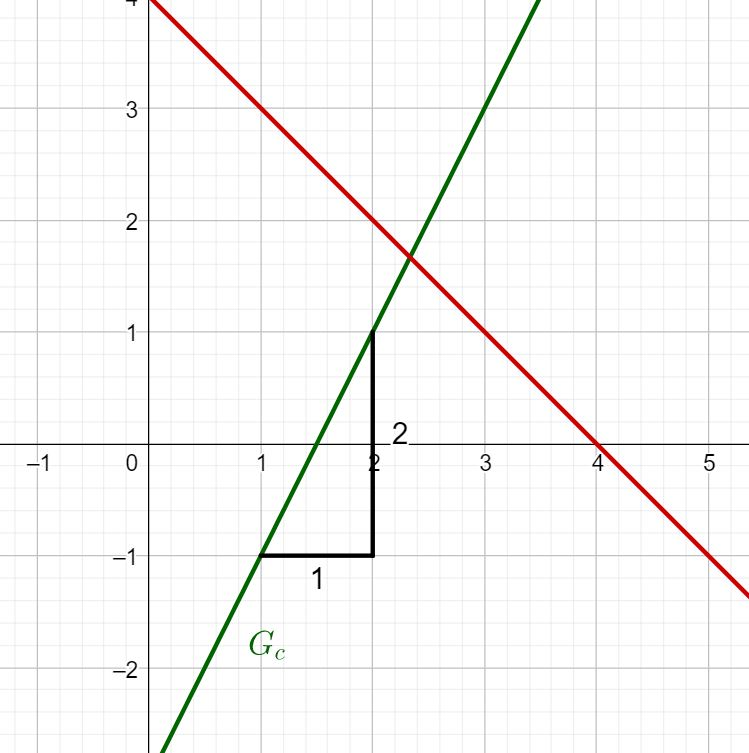
Lies den Schnittpunkt ab.
Gib den Punkt in das Eingabefeld ein. Beispiel: "(-2;1)" oder "(-2|1)"
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt
Schnittpunkte ablesen
Wir lesen aus der Zeichnung den Schnittpunkt ab.
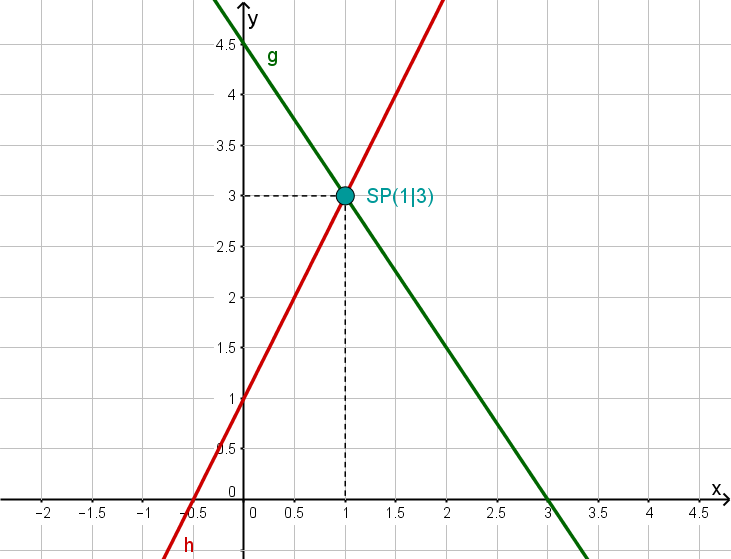
Hast du eine Frage oder Feedback?
- 6
Lies aus dem Graphen die Steigung ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du gehst vom y-Achsenabschnitt (hier ) um nach rechts und um nach oben.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du gehst vom y-Achsenabschnitt (hier ) um nach rechts und um nach unten.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du gehst vom y-Achsenabschnitt (hier ) um nach rechts und um nach oben.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du gehst vom y-Achsenabschnitt (hier ) um nach rechts und um nach unten.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du gehst vom y-Achsenabschnitt (hier ) um nach rechts und um nach oben.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
- 7
Bestimme die Steigung der folgenden Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Der Graph ist steigend. Also können nur Antwortmöglichkeiten 2,5 und 1 richtig sein. Wenn du vom y-Achsenabschnitt (hier ) um nach rechts gehst, musst du etwa eins noch nach oben, um die Gerade wieder zu erreichen.
Deine Steigung lautet also: .
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du sucht dir im Koordinatensystem zwei Punkte, deren Koordianten du leicht ablesen kannst. Hier z.B. und . Um von zu zu kommen, gehst du nach rechts und um nach unten.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Die Gerade ist fallend. Daher kann die Steigung nur negativ sein. als mögliche richtige Lösungen kommen also nur noch oder in Frage.
Wenn du im Koordinatensystem vom y-Achsenabschnitt um nach rechts gehst, musst du weniger als nach unten, um die Gerade wieder zu treffen. Also kann die Antwort nicht stimmen.
Wenn man den Graphen sehr sehr genau ansieht, kommt man auf das Ergebnis:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Der Graph ist steigend, also kann die Steigung nur positiv sein. Die Antwortmöglichkeiten oder oder stehen also noch zur Wahl.
Such dir einen Punkt auf der Geraden, dessen Koordinaten du leicht ablesen kannst. Hier eignet sich zum Beispiel der Punkt . Von hier gehts du um nach rechts und weniger als 2 nach oben, um die Gerade wieder zu erreichen. Daher bleibt nur noch die Antwortmöglichkeit übrig.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Du gehst vom y-Achsenabschnitt (hier ) um nach rechts und um nach unten.
Deine Steigung lautet also:
Hast du eine Frage oder Feedback?
Überlege dir, wie du ein Steigungsdreieck einzeichnen könntest.
- 8
Betrachte die Graphen der Funktionen und . Lies den -Achsenabschnitt und die Steigung der Geraden ab und trage sie in die Felder ein! Kannst du daraus den Funktionsterm aufstellen?
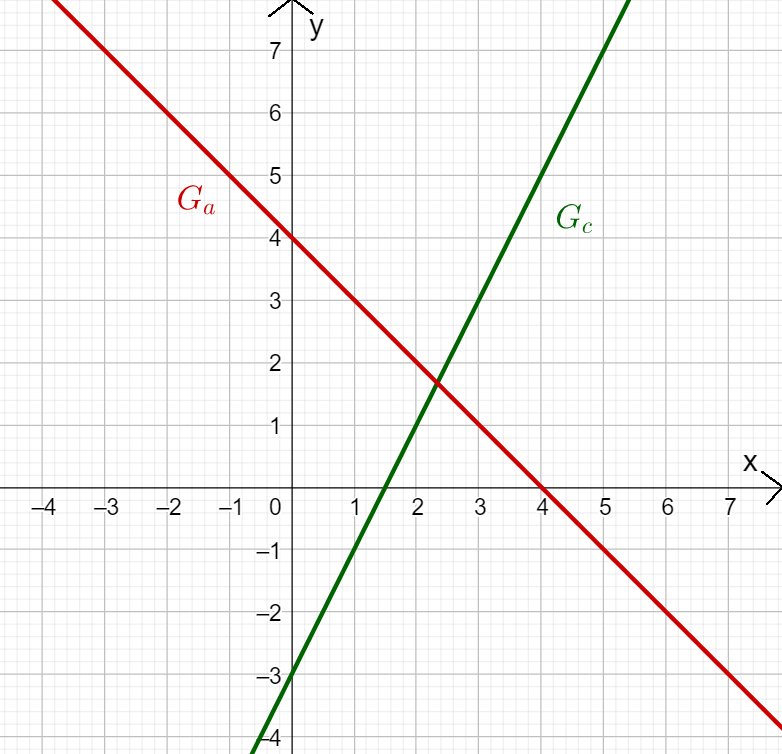
Welchen -Achsenabschnitt hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
-Achsenabschnitt bestimmen
Den -Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Gerade mit der -Achse betrachtest.
In diesem Fall:
Der -Achsenabschnitt ist der -Wert des Schnittpunkts , also .
Hast du eine Frage oder Feedback?
Achte darauf, wo die Gerade die y-Achse schneidet.
Bestimme dann den Schnittpunkt!
Welche Steigung hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Geraden
Steigung bestimmen
Die Steigung einer Geraden bestimmt man am einfachsten mithilfe eines Steigungsdreiecks.
Im Fall von :
Du kannst ablesen, dass du eine Längeneinheit nach unten und eine Längeneinheit nach rechts gehst.
Du erhältst für die Steigung:
Hast du eine Frage oder Feedback?
Kreiere dafür ein Steigungsdreieck (siehe unten).
Bestimme dann die Steigung.
Welchen Funktionsterm hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Funktionsterm aufstellen
Der Funktionsterm einer linearen Funktion hat die Form:
Dabei steht für die Steigung und für den -Achsenabschnitt.
Setzt du die Werte aus den vorigen Teilaufgaben ein erhältst du:
Vereinfacht ist das:
Die Funktionsgleichung von ist also:
.
Hast du eine Frage oder Feedback?
Schau dir das Grundwissen zu der linearen Funktion an.
Setze deine bisherigen Werte in die Funktion ein (siehe unten für eine ausführlichere Erklärung).
Welchen -Achsenabschnitt hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
-Achsenabschnitt bestimmen
Den -Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Gerade mit der -Achse betrachtest.
In diesem Fall:
Der -Achsenabschnitt von ist also .
Hast du eine Frage oder Feedback?
Achte darauf, wo die Gerade die y-Achse schneidet.
Bestimme dann den Schnittpunkt!
Welche Steigung hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Geraden
Steigung bestimmen
Die Steigung einer Geraden bestimmt man am einfachsten mithilfe eines Steigungsdreiecks.
Im Fall von :
Du kannst ablesen, dass du eine Längeneinheit nach rechts und zwei Längeneinheiten nach oben gehst.
Du erhältst für die Steigung:
Hast du eine Frage oder Feedback?
Kreiere dafür ein Steigungsdreieck (siehe unten).
Bestimme dann die Steigung.
Welchen Funktionsterm hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Funktionsterm aufstellen
Der Funktionsterm einer linearen Funktion hat die Form:
Dabei steht für die Steigung und für den -Achsenabschnitt.
Setzt du die Werte aus den vorigen Teilaufgaben ein erhältst du:
Die Funktionsgleichung von ist also:
Hast du eine Frage oder Feedback?
Schau dir das Grundwissen zur linearen Funktion an.
Setze deine bisherigen Werte in die Funktion ein (siehe unten für eine ausführlichere Erklärung).
- 9
Bestimme die Gleichung folgender Gerade:
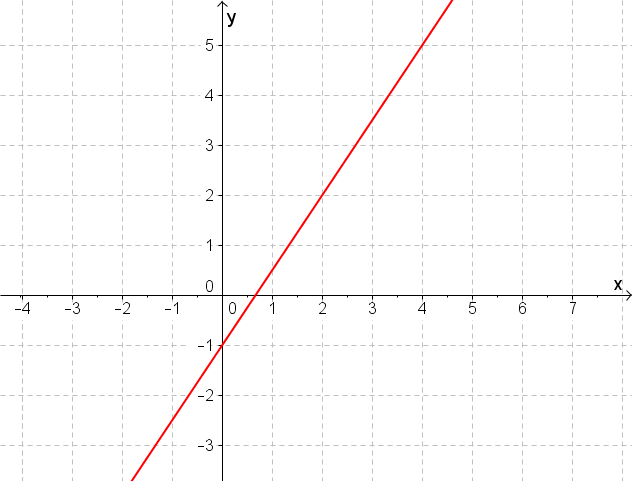
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Die allgemeine Geradengleichung ist:
Lese den y-Achsenabschnitt , also die Stelle, an der die Gerade die y-Achse schneidet, aus der Zeichnung ab.
Suche zwei Punkte mit (bestenfalls) ganzzahligen Koordinaten.
und liegen auf der Gerade.
Um die Steigung zu bestimmen, gibt es zwei Möglichkeiten:
1.
Setze die Koordinaten von und ein!
2.
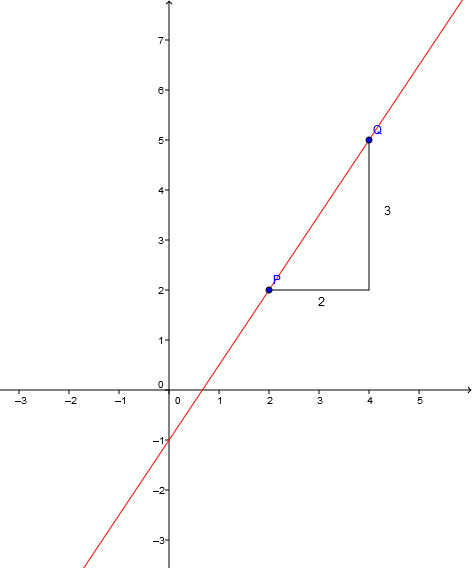
Zeichne ein Steigungsdreieck zwischen den Punkten. Der senkrechte Abstand ist der Zähler, der waagerechte Abstand ist der Nenner des Bruches, der die Steigung beschreibt.
Die Geradengleichung ist also gegeben durch:
- 10
Folgende Abbildungen enthalten Graphen von linearen Funktionen.
Bestimme die Funktionsterme.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies den y-Achsenabschnitt an der Abbildung ab.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab und berechne die Steigung:
Du kannst zum Beispiel diese Punkte verwenden:
und
und
Für die Steigung erhältst du dann durch einsetzen:
Setze die berechneten Werte von und nun in die allgemeine Form ein:
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um die Steigung zu berechnen.
Beispielsweise kannst du diese beiden Punkte verwenden:
und
und
Die Steigung ist dann:
Da der y-Achsenabschnitt nicht sichtbar ist, musst du ihn berechnen. Stelle dafür die Geradengleichung auf.
Setze einen der Punkte ein, zum Beispiel .
Löse nun nach auf.
Setze die Werte von und in die allgemeine Form der linearen Funktion ein und du bekommst die Geradengleichung:
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um die Steigung zu berechnen.
Du kannst zum Beispiel diese beiden Punkte verwenden:
und
und
Mit ihnen kannst du nun die Steigung berechnen:
Lies entweder ab oder berechne den Wert. Um ihn zu berechnen, stelle die Geradengleichung auf.
Setze einen Punkt ein, der auf der Gerade liegt, zum Beispiel .
Löse nun noch nach auf.
Setze und in die allgemeine Form ein und du erhältst die Geradengleichung:
Hast du eine Frage oder Feedback?
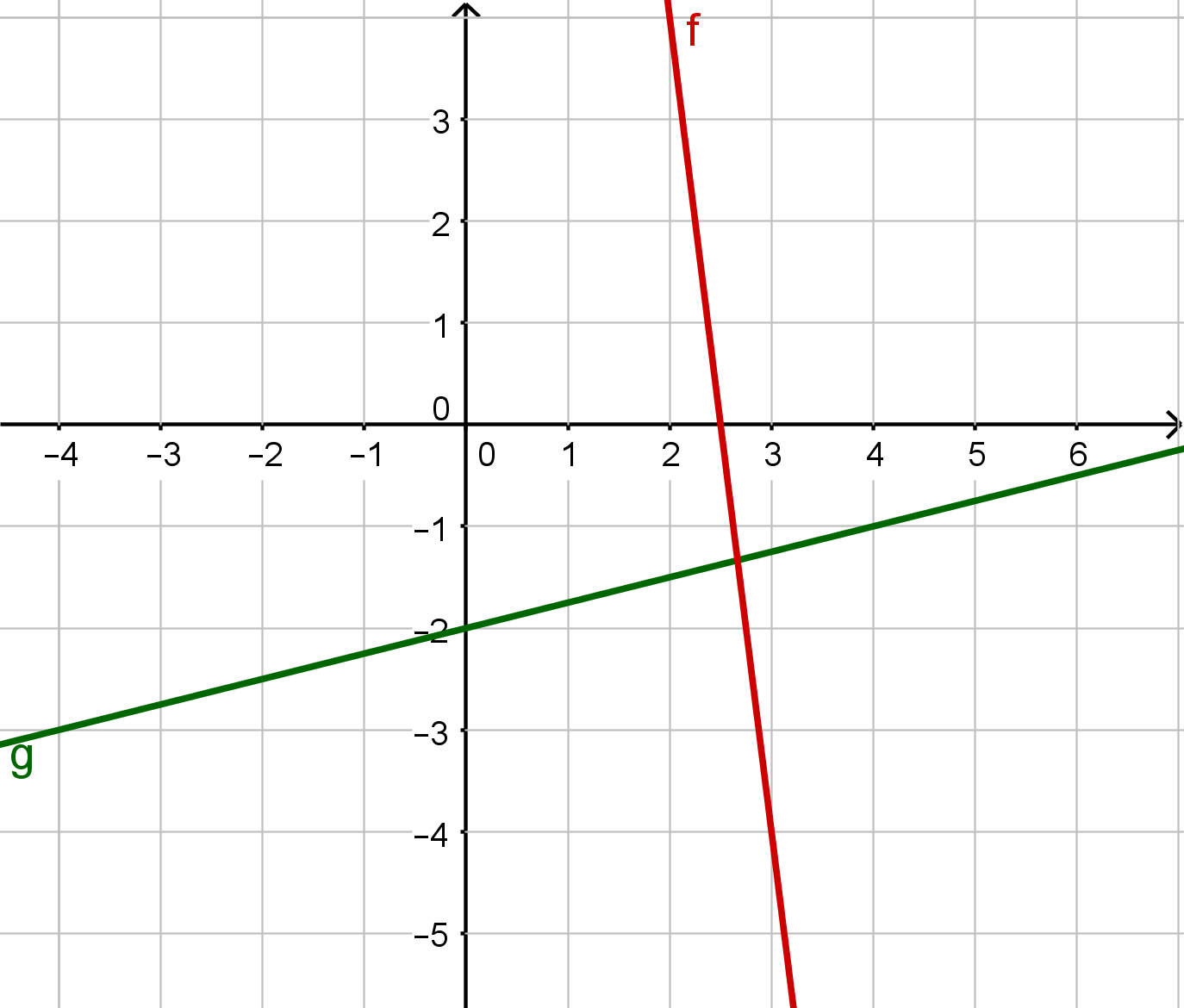
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um mit ihnen die Steigung zu berechnen:
Du kannst zum Beispiel diese beiden Punkte verwenden:
und
und
Als Steigung ergibt sich:
Da der y-Achsenabschnitt nicht sichtbar ist, musst du ihn berechnen. Stelle daher die Geradengleichung auf:
Setze einen der Punkte, zum Beispiel , ein:
Löse nach auf.
Setze und in die allgemeine Form ein und du bekommst als Ergebnis die Geradengleichung:
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um mit ihnen die Steigung zu berechnen:
Du kannst zum Beispiel diese beiden Punkte verwenden:
und
und
Berechne mit ihnen nun die Steigung:
Lies den y-Achsenabschnitt an der Abbildung ab.
Setze und in die allgemeine Form der linearen Funktion ein und du erhältst die Geradengleichung von :
Hast du eine Frage oder Feedback?
- 11
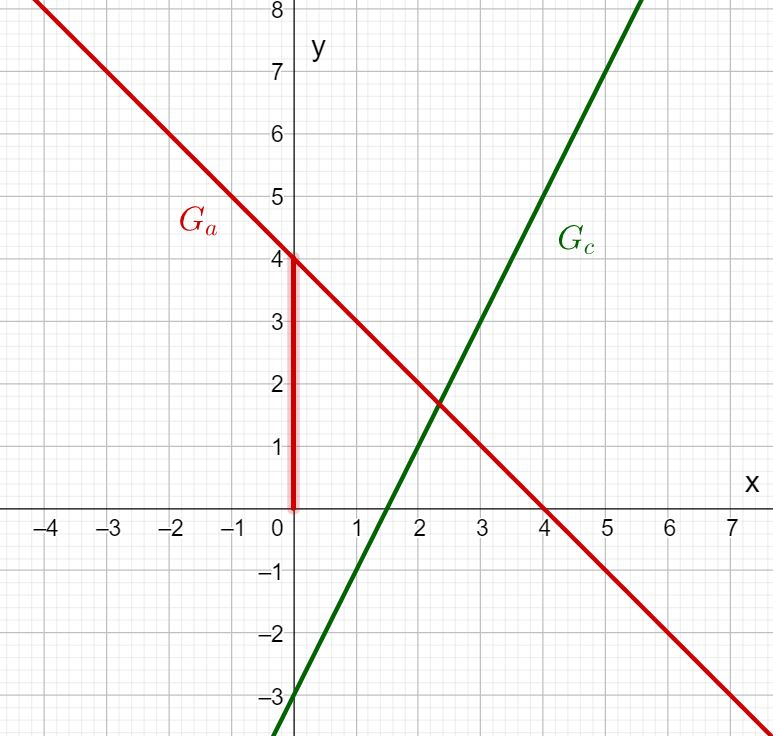
Gegeben sind die folgenden Funktionsgraphen:
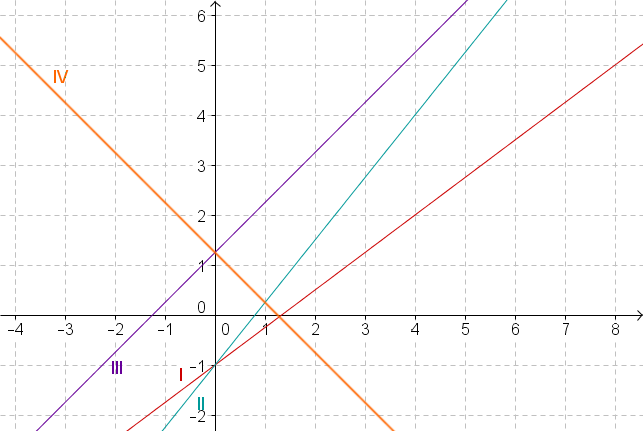
Welcher der vier Graphen gehört zur Gleichung
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
Vorgegebene Graphengleichung:
Du kannst die Steigung und den y-Achsenabschnitt dieses Graphen an der Gleichung ablesen.
Überprüfe zuerst bei welchen Funktionen der y-Achsenabschnitt beträgt, indem du den y-Wert jedes Graphen abliest, indem die y-Achse geschnitten wird.
Nur Graph I und II haben den y-Achsenabschnitt also kannst du jeden anderen Graphen ausschließen.
Überprüfe nun welcher der beiden Graphen die Steigung besitzt, indem du vom Punkt ausgehend eins nach rechts gehst und überprüfst, welcher der beiden y-Werte sich um erhöht.
Beide Graphen beginnen beim Punkt . Da die gesuchte Gerade die Steigung hat, geht sie auch durch den Punkt .
Durch diesen Punkt läuft nur die Gerade II.
Der Graph II ist der Graph, der zu der vorgegebenen Gleichung gehört.
Hast du eine Frage oder Feedback?
Wie lautet die Gleichung zum Graphen III?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
zu überprüfende Gerade: Graph III
Lies zuerst wo der Graph die y-Achse schneidet, um den y-Achsenabschnitt zu ermitteln.
Der y-Wert des Punktes, indem die y-Achse geschnitten wird, beträgt . Somit ist .
Lies nun ab um wieviel sich der y-Wert verändert, wenn du ausgehend von , eins nach rechts gehst. Dadurch ermittelst du die Steigung.
Der y-Wert erhöht sich von auf . Somit beträgt die Steigung .
Stelle die Gleichung auf.
⇒ Der Graph III hat die Gleichung
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?