Was ist eine Funktion?

Bemerkung: Häufig bezeichnet man Funktionen mit einem einzelnen Buchstaben. Der gewöhnlichste Name für eine Funktion ist $f$.

Mit diesem Namen kann man einfach verdeutlichen, dass $y$ der Funktionswert an der Stelle $x$ ist, indem man $y=f(x)$ schreibt. Gelesen wird dies "$y$ ist gleich $f$ von $x$".

Beispiele von Funktionen

Beispiel 1

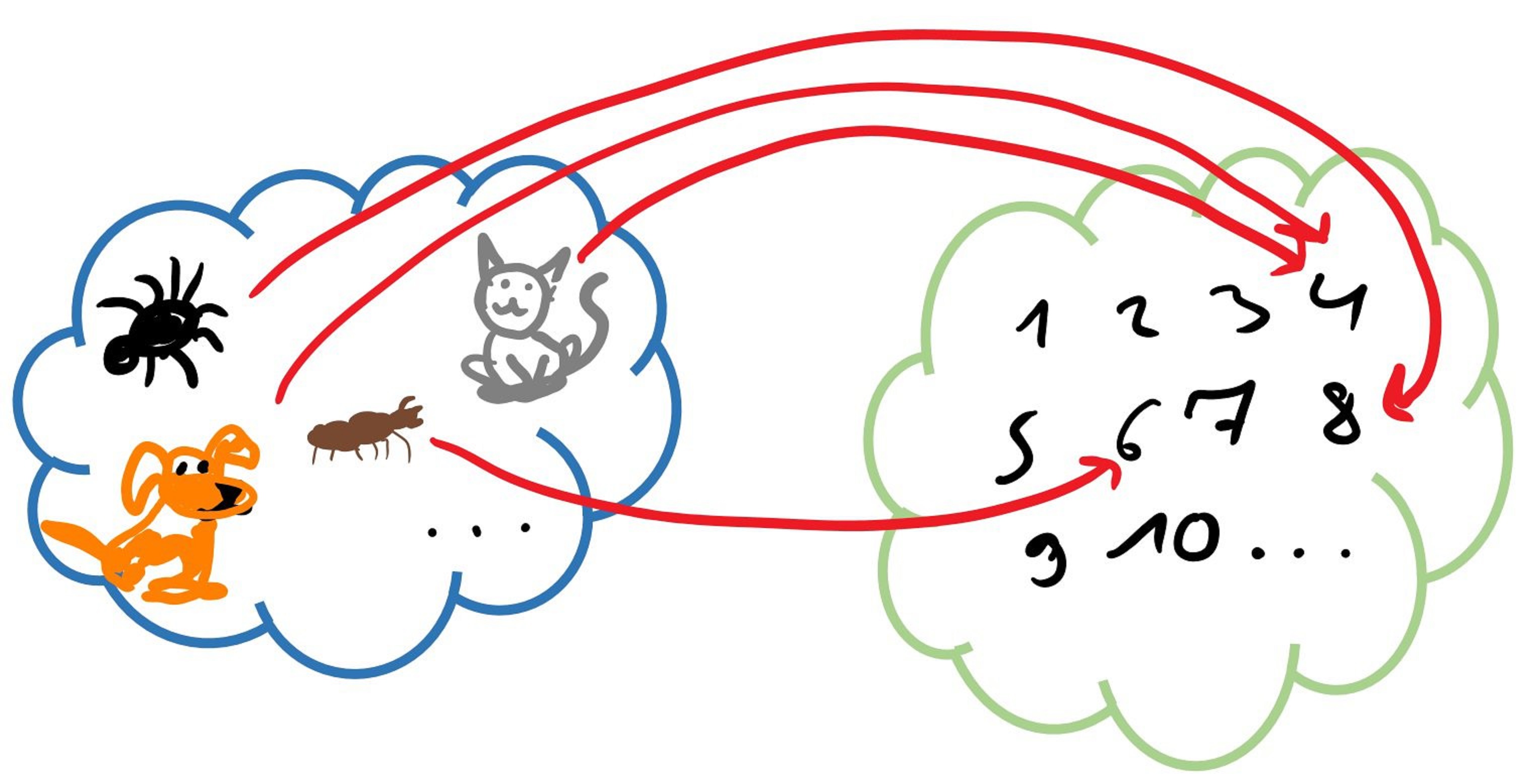
Beispiele für Funktionswerte sind dann:

• $f(\text{Katze})=4$ ("der Funktionswert an der Stelle Katze ist $4$")

• $f(\text{Spinne})=8$ ("$f$ von Spinne ist gleich $8$")

• $f(\text{Ameise})=6$ ("$f$ von Ameise ist gleich $6$")

• $f(\text{Hund})=4$ ("$f$ von Hund ist gleich $4$")

Warum ist $f$ eine Funktion?

Ganz einfach:

• $f$ hat einen Definitionsbereich (die Menge aller Tierarten).

• $f$ hat einen Wertebereich (die Menge ${\mathbb{N}}_{\mathrm{𝟘}}$ aller natürlichen Zahlen mit der Null)

• und jeder Tierart kann eindeutig eine solche Anzahl an Beinen zugeordnet werden.

Beispiel 2

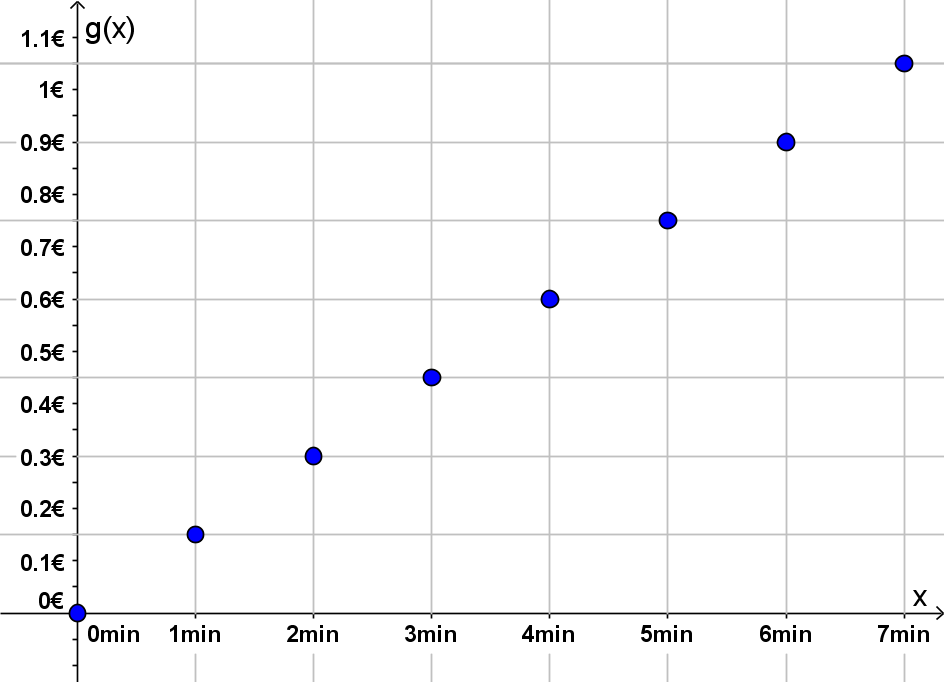
Der Definitionsbereich ist in diesem Beispiel durch die natürlichen Zahlen inklusive der Null gegeben (${\mathbb{N}}_0$). Denn laut der Aufgabenstellung wird bei der Minutenangabe aufgerundet.

Am Graphen ist gut erkennbar, dass je länger man telefoniert, die Kosten steigen. Somit können Funktionen gut Zusammenhänge wiedergeben.

Beispiel 3

$h$ soll die Funktion sein, die jeder natürlichen Zahl das Doppelte ihres Wertes zuordnet. Für jede Zahl ist diese Zuordnung offensichtlich eindeutig.

Beispiele für Funktionswerte:

• $h(1)=2\cdot 1=2$ (das Doppelte von 1 ist 2)

• $h(3)=2\cdot 3=6$

• $h(4)=8$

• $h(7)=14$

Oft verwendete Schreibweisen

An einem Beispiel sollen die häufig verwendeten Bezeichnungen gegenüber gestellt werden.

Am Anfang steht die Zuordnungsvorschrift, sie legt den Namen, die Variable und den Wert der Funktion fest:

Weil die Funktionswerte sehr oft mit einer Formel, also einem Term berechnet werden, gibt man statt y meistens gleich diesen Term an

Zum Beispiel:

Diese Funktion heißt also $f$. Sie ordnet jeder Einsetzung für $x$ eine Wert $y$ zu, der mit dem Funktionsterm $f(x)$ berechnet wird. Die Einsetzungen werden aus der Definitionsmenge $D$ gewählt. Häufige andere Bezeichnungen sind $g$ oder mit Index, zum Beispiel $f_1$ oder $g_3$.

Damit ist schon geklärt, was es mit dem Funktionsterm auf sich hat. Bei jedem Term werden die Termvariablen in Klammern angegeben. In den meisten Fällen gibt es nur die Variable $x$. Dann heißt der Funktionsterm eben $f(x)$ oder $g(x)$ oder $f_3(x)$, je nachdem welche Bezeichnung die Funktion erhalten hat.

Es liegt also eine Gleichung mit zwei Variablen vor.

Der Funktionsterm kann also Bestandteil der Zuordnungsvorschrift oder der Funktionsgleichung sein.

Diese Sichtweise ist wichtig, wenn man Funktionen über ihre Wertepaare $(x,y)$ in eine $x$-$y$-Koordinatensystem einträgt. Diese Menge von Punkten, die durch die Wertepaare gebildet werden, nennt man den Graphen der Funktion $f$, man bezeichnet ihn mit $G_f$. Der Graph ist die Menge aller Punkte:

Wichtig: Oft werden für Funktionsnamen und Variable andere Buchstaben verwendet. In der Physik verwendet man zum Beispiel t als Variable, wenn $t$ dabei die Zeit beschreiben soll (tempus ist das lateinische Wort für Zeit).

Betrachtet man mehrere Funktionen gleichzeitig, bietet es sich an, eine als $f$, eine als $g$, eine als $h$ und so weiter zu bezeichnen.

Besondere Eigenschaften von Funktionen

Stetigkeit 

Eine Funktion $f$ heißt genau dann stetig an einer Stelle $x_0$, wenn der Funktionswert an dieser Stelle mit sowohl dem links- als auch rechtsseitigem Grenzwert identisch ist, d. h. wenn gilt:

$f(x_0)={\lim }_{x\to x_0^{-}}f(x)={\lim }_{x\to x_0^{+}}f(x)$

Mehr zum Thema in unserem Artikel Stetigkeit.                             

Differenzierbarkeit

Eine Funktion $f$ heißt differenzierbar an einer Stelle $x_0$ ihres Definitionsbereichs, falls der Differentialquotient existiert:

${\lim }_{x\to x_0}{\displaystyle \frac{f(x)-f(x_0)}{x-x_0}}$

Mehr zum Thema in dem Artikel Differenzierbarkeit.

Periodizität einer Funktion

Eine reelle Zahl $T$ heißt Periode einer Funktion, wenn für alle Elemente $x$ aus der Definitionsmenge gilt: $f(x)=f(x+T)$.

Die Funktion hat also im "Abstand $T$" immer den gleichen Funktionswert.

Anders ausgedrückt:

Verschiebt man den Graphen in $x$-Richtung um $T$, so ändert sich der Funktionsgraph nicht.

Mehr zum Thema in dem Artikel Periode (einer Funktion)

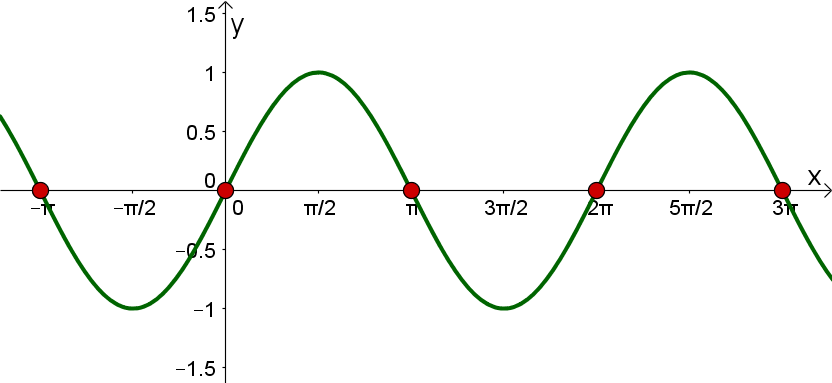
Umkehrfunktion   

Die Umkehrfunktion $f^{-1}$ einer Funktion $f$ bezeichnet die Funktion, die die Funktionswerte $f(x)$ wieder auf ihre Argumente $x$ abbildet (wenn so eine Funktion existiert, also wenn $f$ umkehrbar ist). Die Umkehrfunktion existiert nur, wenn jeder Wert in der Wertemenge höchstens einmal "getroffen" wird.

Mehr zum Thema auf unserer Partnerseite www.brinkmann-du.de.