Aufgaben zum Rechnen mit Brüchen - ohne negative Zahlen
Hier findest du Aufgaben, in denen du das Rechnen mit Brüchen üben kannst. Lerne, Brüche aufzustellen und Rechengesetze mit Brüchen anzuwenden!
- 1
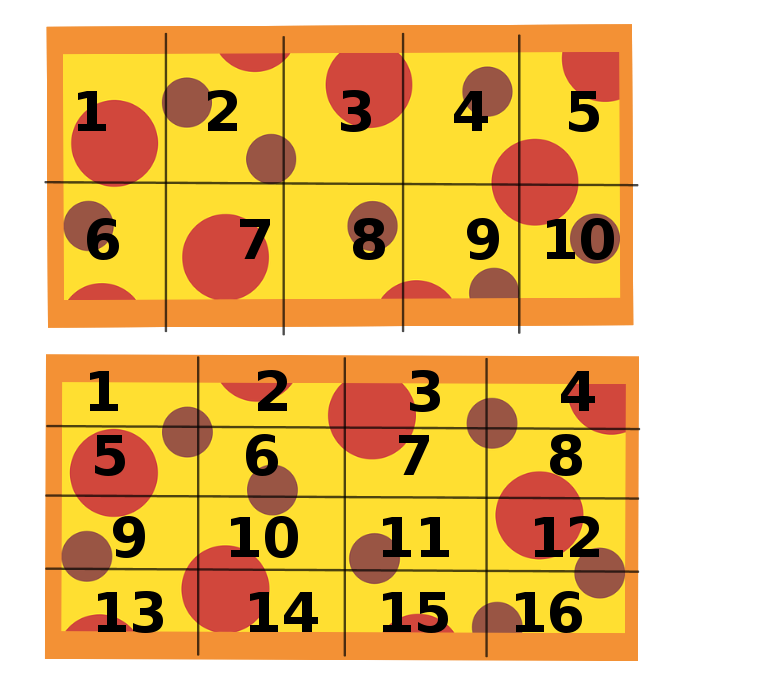
Denke dir eine Textaufgabe zu folgender Situation aus und löse sie! (Hinweis: Im Bild sind zwei gleich große Pizzen zu sehen. Die Pizzastücke einer Pizza haben immer dieselbe Größe.)
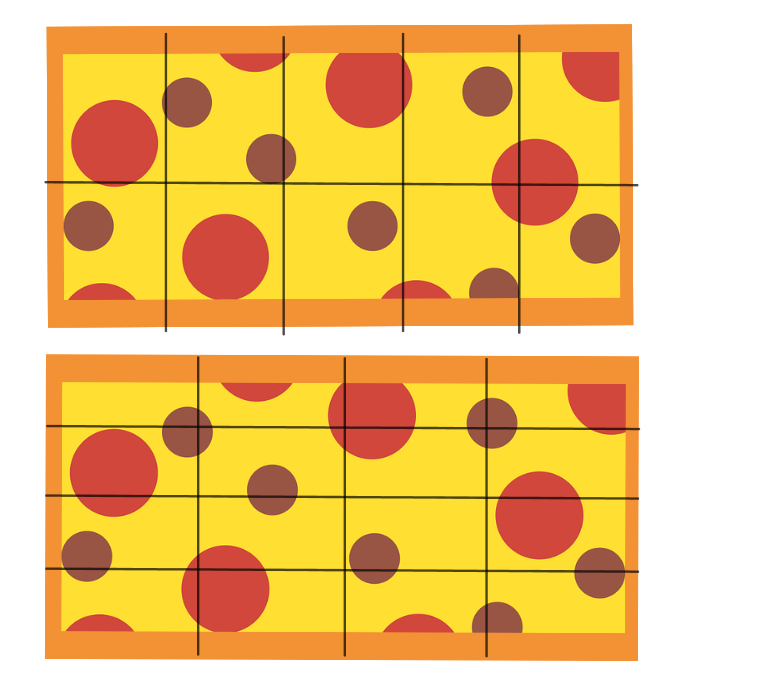
20 Minuten später:
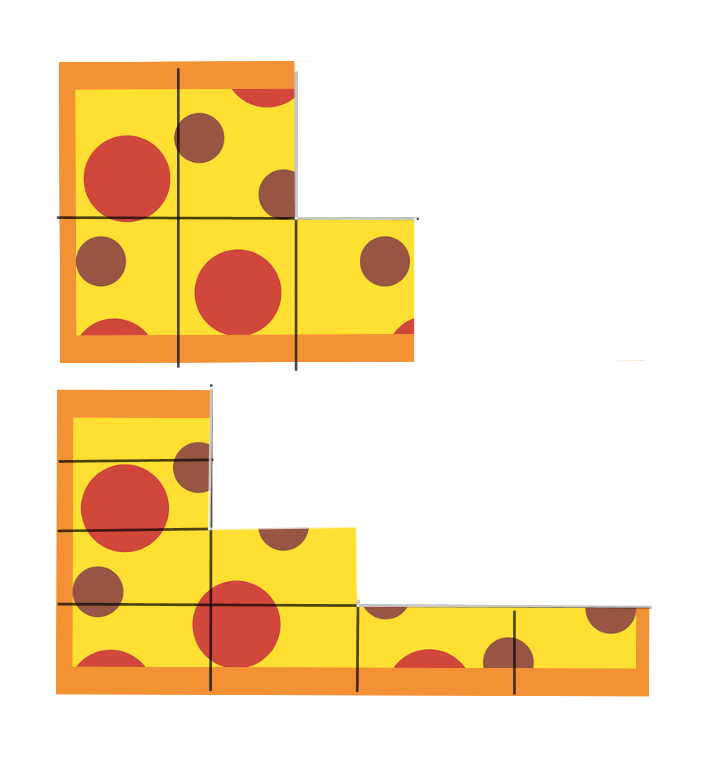
- 2
Berechne den Wert des Terms . Gib das Ergebnis als Bruch der Form a/b, z.B. 4/5, ein.
- 3
Welche Aussagen über den Bruch sind wahr? Wähle alle richtigen Antworten aus!
- 4
Berechne den Wert des Terms . Gib dein Ergebnis als Bruch der Form a/b ein!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?