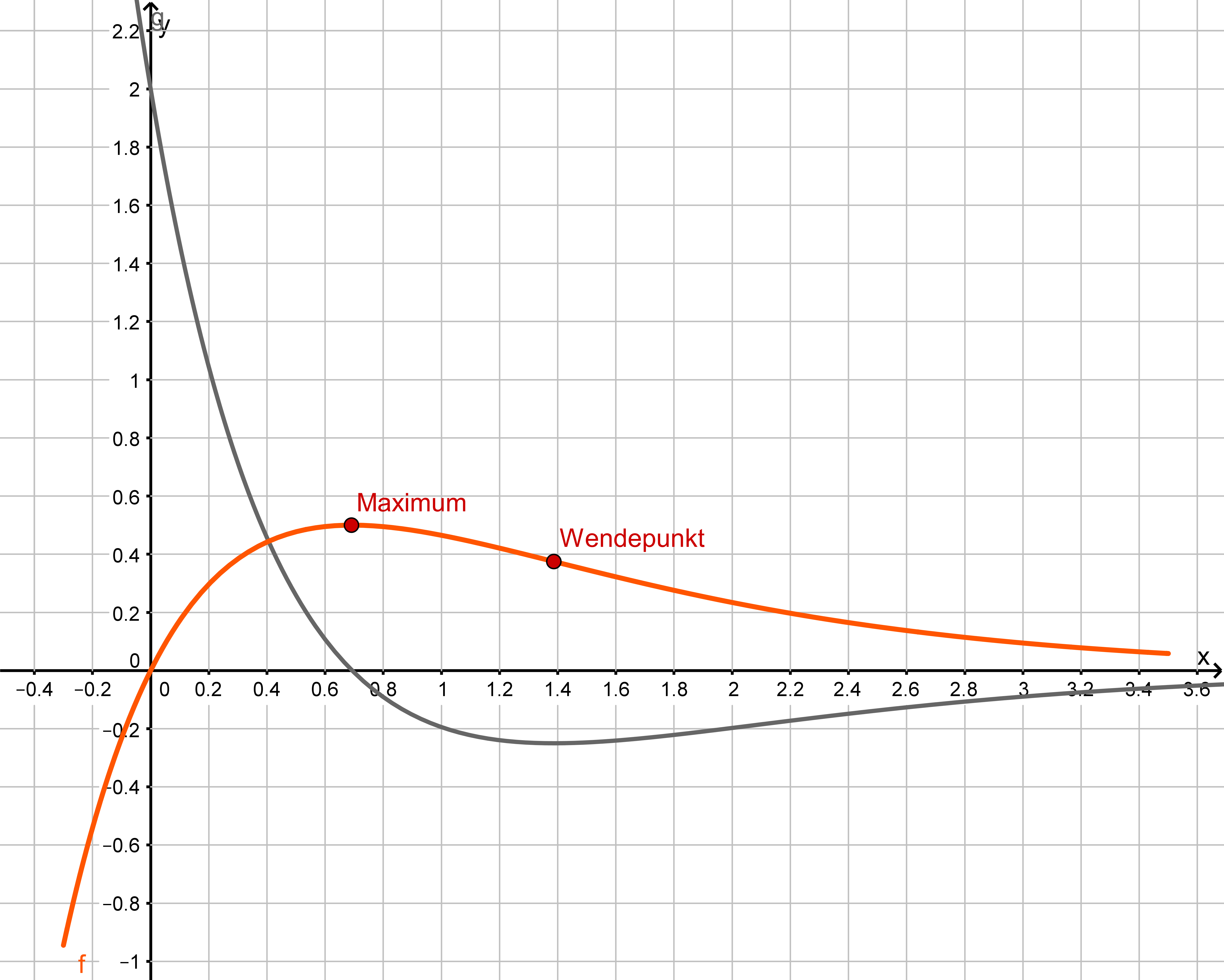
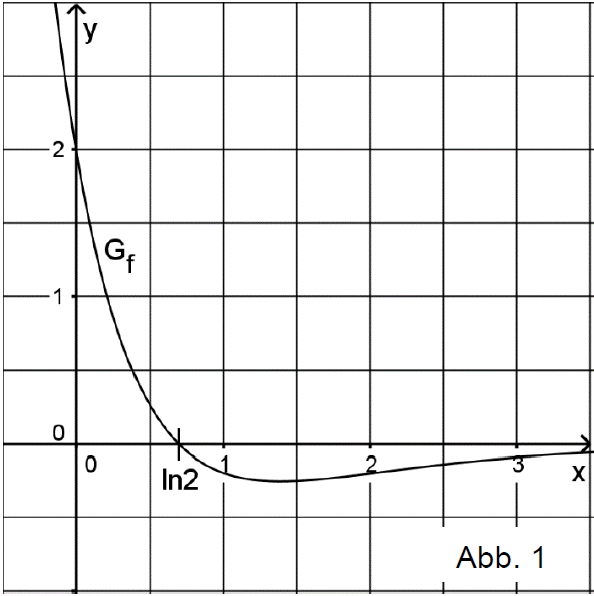
Gegeben ist die Funktion mit und . Abbildung 1 zeigt den Graphen von sowie die einzige Nullstelle von .
Zeigen Sie, dass für den Term der Ableitungsfunktion von gilt: . (3 BE)
Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von . (4 BE)
(Teilergebnis: x-Koordinate des Extrempunkts: )
Zusätzlich ist die Funktion mit und gegeben.
Zeigen Sie, dass eine Stammfunktion von ist, und begründen Sie anhand des Terms von , dass gilt. (3 BE)
Der Graph von verläuft durch den Punkt . Begründen Sie ohne weitere Rechnung, dass keine größeren Werte als annehmen kann und bei eine Wendestelle besitzt. Berechnen Sie die y-Koordinate des zugehörigen Wendepunkts. (5 BE)
Zeichnen Sie den Graphen von unter Berücksichtigung der bisherigen Ergebnisse sowie des Funktionswerts im Bereich in Abbildung 1 ein. (4 BE)
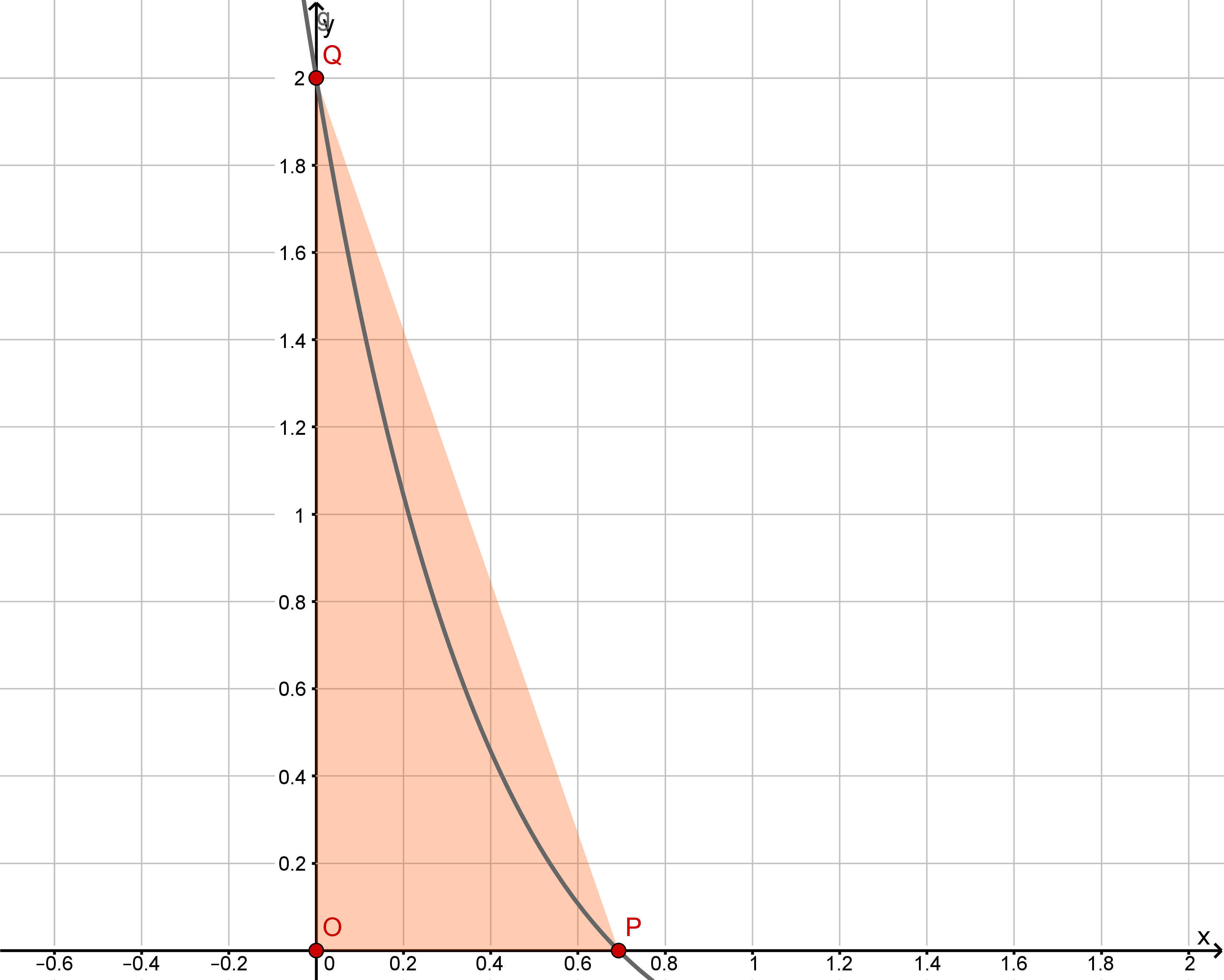
Der Graph von schließt mit den Koordinatenachsen ein Flächenstück ein, das durch das Dreieck mit Eckpunkten , und angenähert werden kann. Berechnen Sie, um wie viel Prozent der Flächeninhalt des Dreiecks vom Inhalt des Flächenstücks abweicht. (4 BE)
Betrachtet wird nun die Integralfunktion mit und .
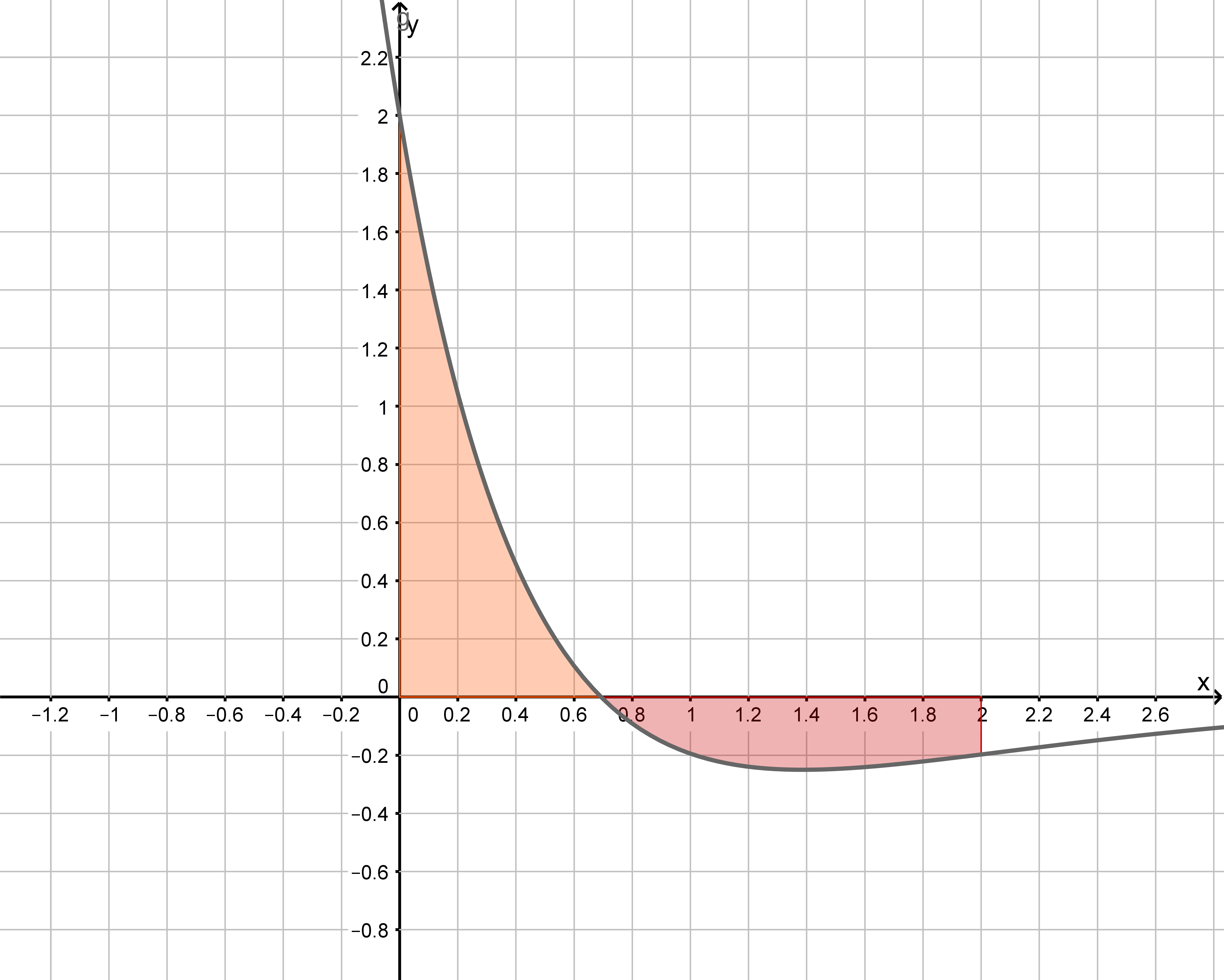
Begründen Sie, dass mit der betrachteten Stammfunktion von übereinstimmt. Interpretieren Sie geometrisch den Wert mithilfe von in Abbildung 1 geeignet zu markierenden Flächenstücken. (4 BE)
Geben Sie den Term einer in definierten Funktion an, die eine Stammfunktion, aber keine Integralfunktion von ist. (2 BE)