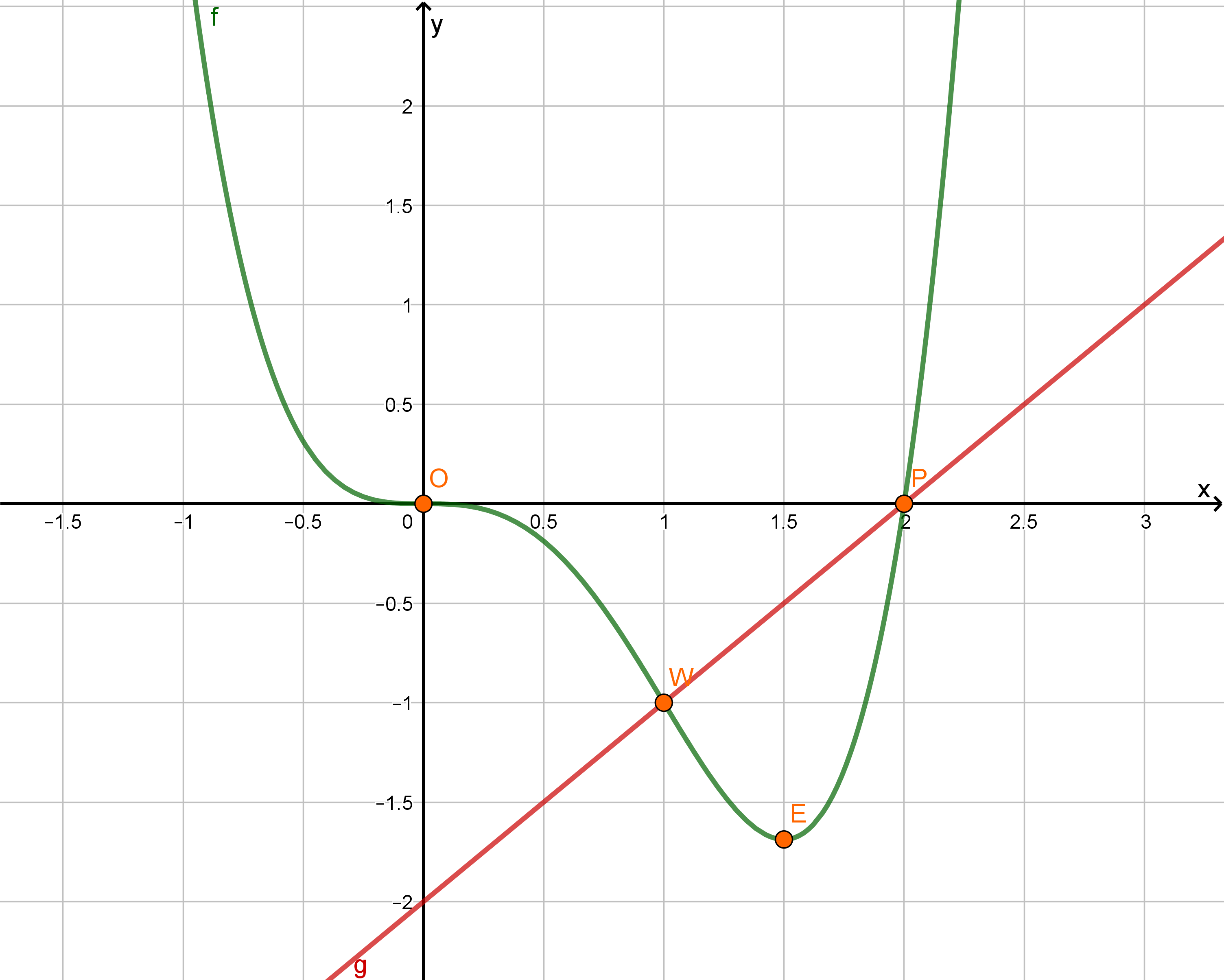
Der Graph einer in definierten Funktion mit besitzt im Punkt O einen Wendepunkt mit waagrechter Tangente.
W ist ein weiterer Wendepunkt von . Bestimmen Sie mithilfe dieser Information die Werte von und . (4 BE)
Bestimmen Sie Lage und Art des Extrempunkts von . (4 BE)
Die Gerade schneidet in den Punkten und .
Zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse sowie die Gerade in ein Koordinatensystem ein. Geben Sie die Gleichung der Geraden an. (4 BE)
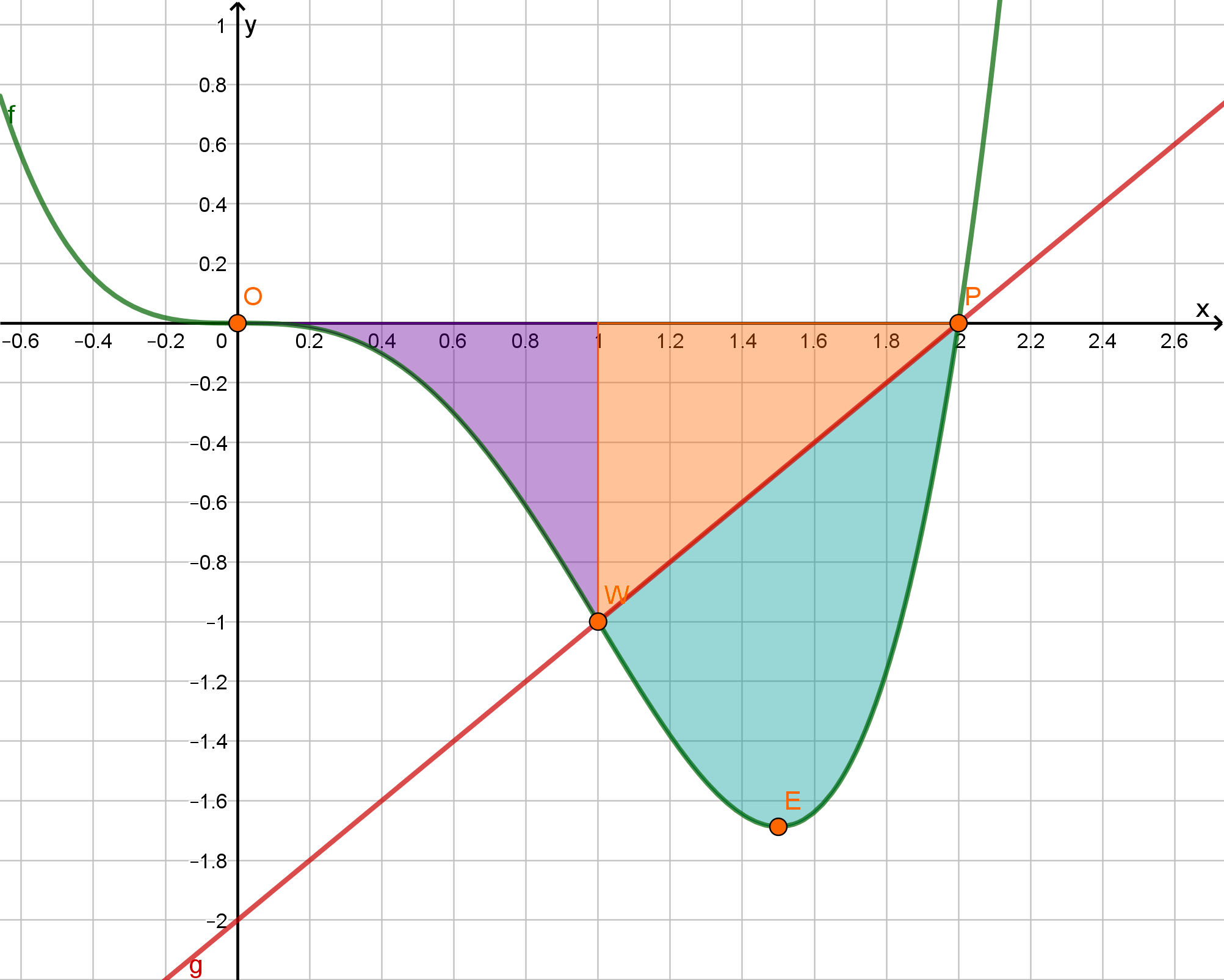
und die x-Achse schließen im IV. Quadranten ein Flächenstück ein, das durch die Gerade in zwei Teilflächen zerlegt wird. Berechnen Sie das Verhältnis der Flächeninhalte dieser beiden Teilflächen. (6 BE)