1 Übersicht
Inhalt des Kurses
Du lernst das Rechenverfahren der Polynomdivision kennen und kannst es sicher durchführen.
Vorkenntnisse
Grundrechenarten, vor allem die schriftliche Division ganzer Zahlen
Definition von Polynomen

Kursdauer:
ca. 3 Stunden
2 Du kannst schon ziemlich viel
Mit Polynomen kannst du schon ganz gut rechnen. Du kannst sie…
Aber kannst du auch schon Polynome dividieren?
kannst du bereits berechnen. Hierfür benutzt du die Potenzgesetze:
.
Aber wie kannst du zum Beispiel berechnen?
Genau das lernst du in diesem Kurs.
3 Das Distributivgesetz der Division
Beim Dividieren von Polynomen muss man das Distributivgesetz der Division beachten. Die Distributivgesetze verbinden die Strichrechnung (Addition und Subtraktion) mit der Punktrechnung (Multiplikation und Division).
Das Distributivgesetz der Division lautet:
Beispiele:

Achtung Falle!
Beispiel:
denn richtig ist:
denn richtig ist:

4 Übungsaufgaben zum Distributivgesetz der Division
Löse die Klammern auf. Entscheide, ob du dafür das Distributivgesetz der Division nutzen kannst oder nicht.
Laden
Laden
Laden
Laden
Weitere Aufgaben zur Anwendung des Distributivgesetzes der Division findest du bei den Vorübungen zur Polynomdivision.
5 Schriftliche Division ganzer Zahlen
Zunächst wiederholen wir, wie du ganze Zahlen schriftlich dividierst. So kannst du später die Polynomdivision leichter nachvollziehen.
Die wesentlichen, sich in der Regel wiederholenden Arbeitsschritte, des schriftlichen Dividierens sind:
Dividieren (ganzzahlig) der ersten Ziffern
Multiplizieren als "Probe"
Subtrahieren als Restbildung

Beispiel
1. Berechnung der 1. Stelle
Dividieren: Teile .
Die passt mal in die .
Multiplizieren: Multipliziere nun .
Wir erhalten .
Subtrahieren: Berechne .
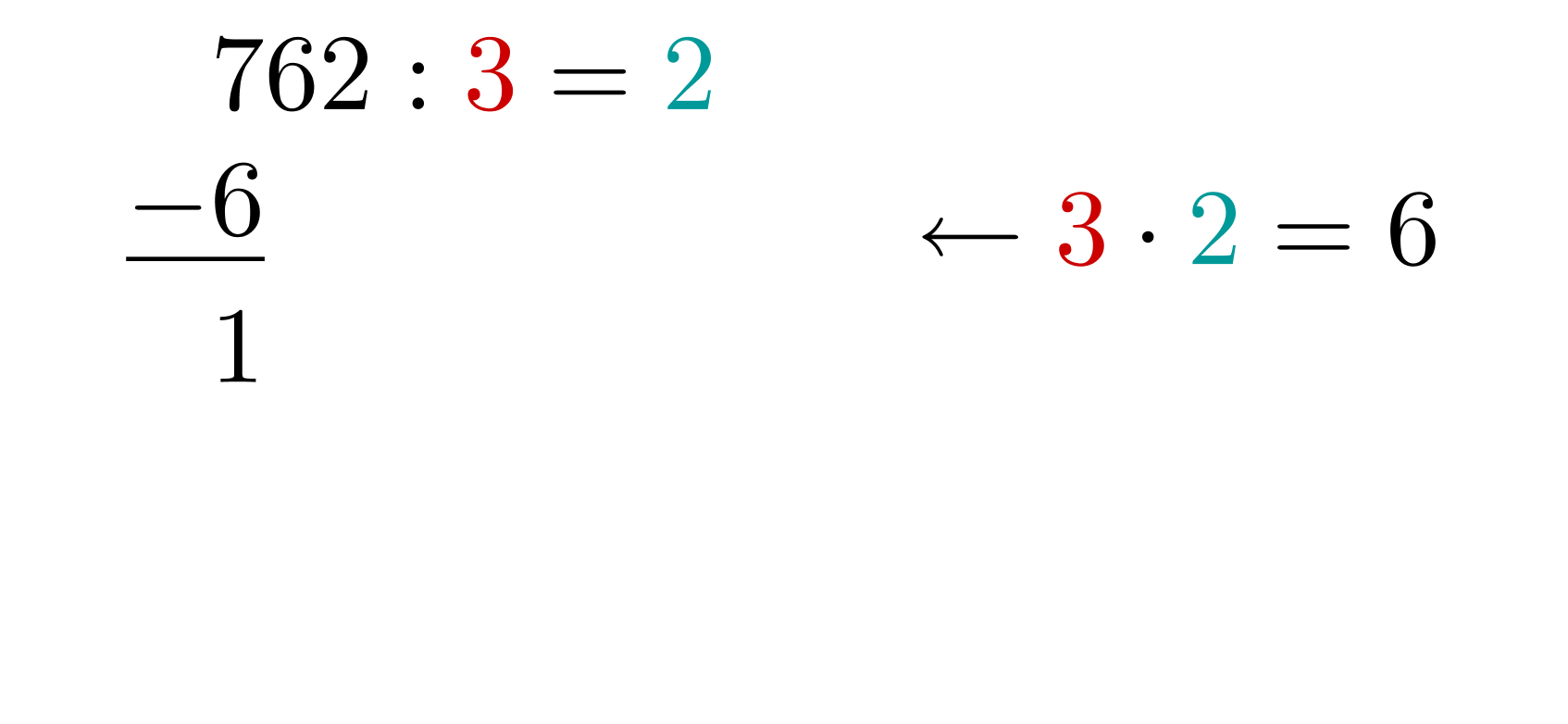
2. Berechnung der 2. Stelle
Dividieren: Nehme zum Rest die nächste Stelle von oben herunter, also die und teile nun .
Die passt mal in die .
Multiplizieren: Multipliziere .
Wir erhalten .
Subtrahieren: Berechne .
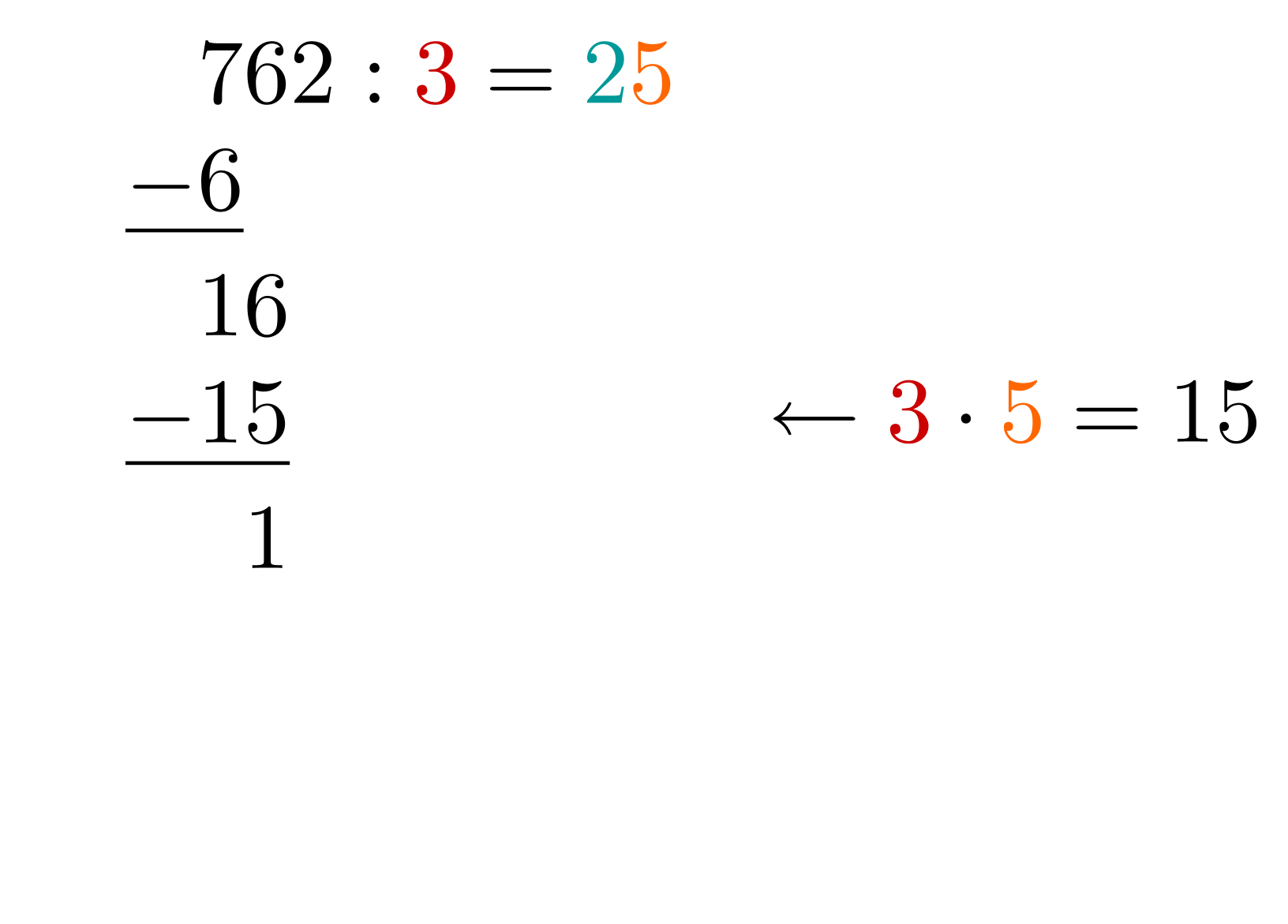
3. Berechnung der 3. Stelle
Dividieren: Nehme zum Rest die nächste Stelle von oben herunter, also die und teile nun .
Die passt mal in die .
Multiplizieren: Multipliziere .
Wir erhalten .
Subtrahieren: Berechne .

Im folgenden Applet kannst du die Arbeitsschritte in einem weiteren Beispiel nachvollziehen. Sie werden auch für die Technik von Polynomdivisionen gebraucht.
6 Übungsaufgaben zur Division ganzer Zahlen
Führe die Divisionen folgender Aufgaben ohne Benutzung eines Taschenrechners aus.
Laden
Laden
Laden
7 Geordnete Polynome
Um die Polynomdivision anwenden zu können, hilft es dir, wenn du die Polynome erst ordnest. Aber was heißt hier ordnen? Ein Polynom heißt geordnet, wenn das Polynom zusammengefasst und nach fallenden Exponenten sortiert ist.

Beispiele für Polynome
nicht zusammengefasst und ungeordnet:
zusammengefasst und ungeordnet:
geordnet:
Übungsaufgaben
Ordne die fogenden Polynome. Fasse zuerst zusammen, falls nötig.
Laden
Laden
Laden
Laden
Weitere Übungsaufgaben zum Ordnen von Polynomen findest du im Aufgabenorder zum Thema Potenzen und Polynome.
8 Polynomdivision (1/2)
Nachdem wir jetzt nochmal wiederholt haben, wie man schriftlich dividiert und wie man Polynome ordnet, versuchen wir nun dieses Wissen auf die Division von Polynomen zu übertragen.
Wir berechnen .
Auch hier gilt: Dividieren macht Spaß!!!

Vorbereitung zur Polynomdivision
Zunächst müssen wir prüfen, ob der Dividend und der Divisor geordnet sind, also die Terme zusammengefasst und absteigend nach den vorkommenden Exponenten sortiert sind.
Der Dividend ist zusammengefasst, da keine Potenz doppelt vorkommt, aber nicht absteigend nach den Potenzen sortiert. Durch Sortieren erhalten wir als geordnetes Polynom .
Der Divisor ist bereits geordnet.
Wir berechnen nun:
… auf der nächsten Kursseite.
9 Polynomdivision (2/2)
Mithilfe der Polynomdivision können wir berechnen.
1. Berechnung der 1. Stelle
Dividieren: Wir teilen nun das erste Monom des Dividenden durch das erste Monom des Divisors und schreiben das Ergebnis hinter das Gleichheitszeichen. Also:

Multiplizieren: Multipliziere nun mit dem gesamten Divisor und schreibe das Ergebnis unter den Dividenden.
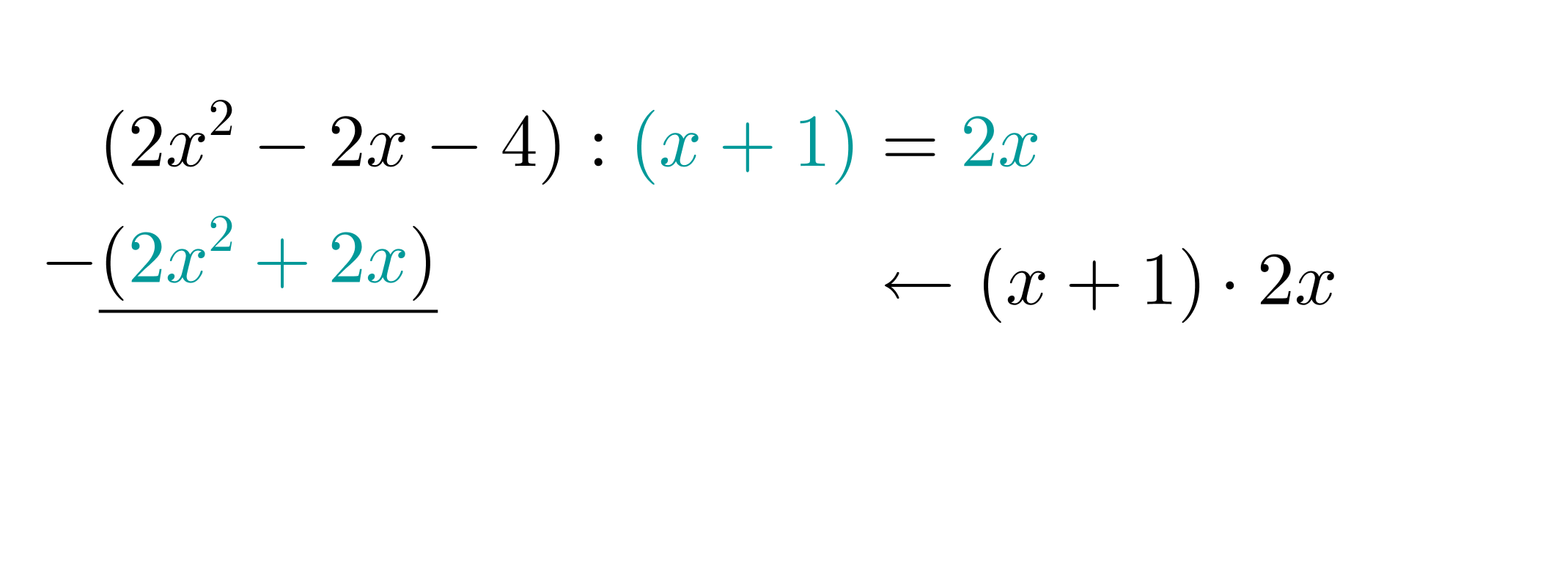
Subtrahieren: Ziehe nun vom Dividenden ab und schreibe die Potenz mit dem nächst kleineren Exponenten neben dein Ergebnis.
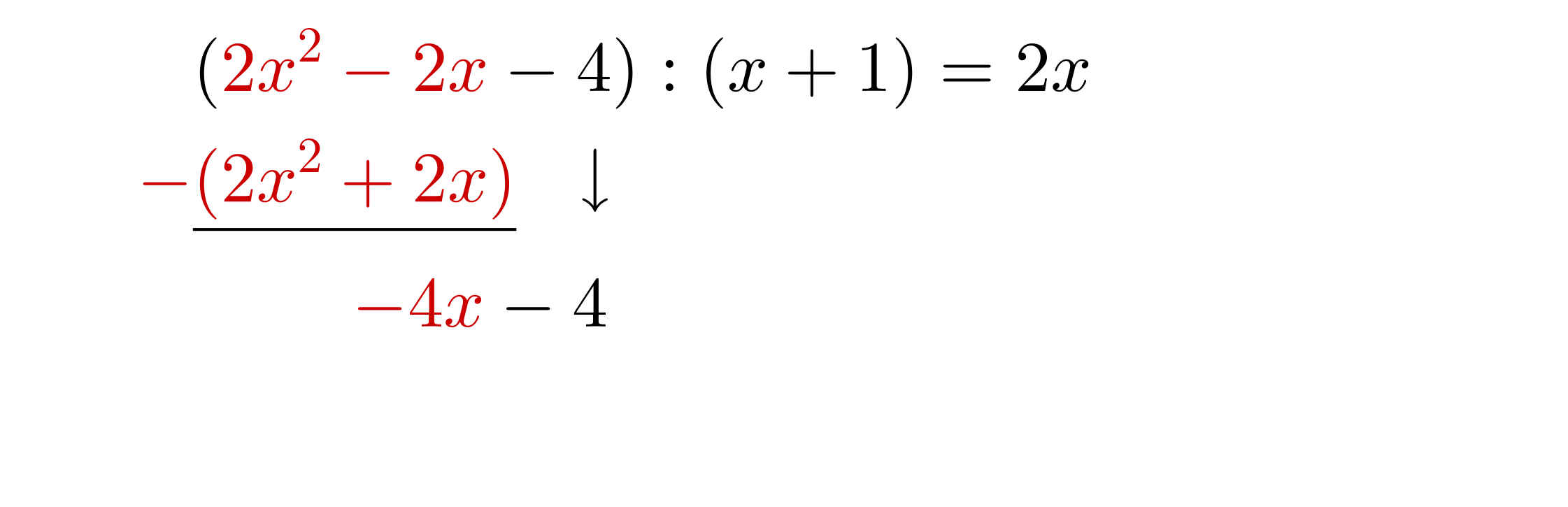
2. Berechnung der 2. Stelle
Dividieren: Teile nun durch das erste Monom des Divisors und schreibe das Ergebnis hinter das Gleichheitszeichen.

Multiplizieren: Multipliziere nun und den Divisor. Schreibe das Ergebnis unter .
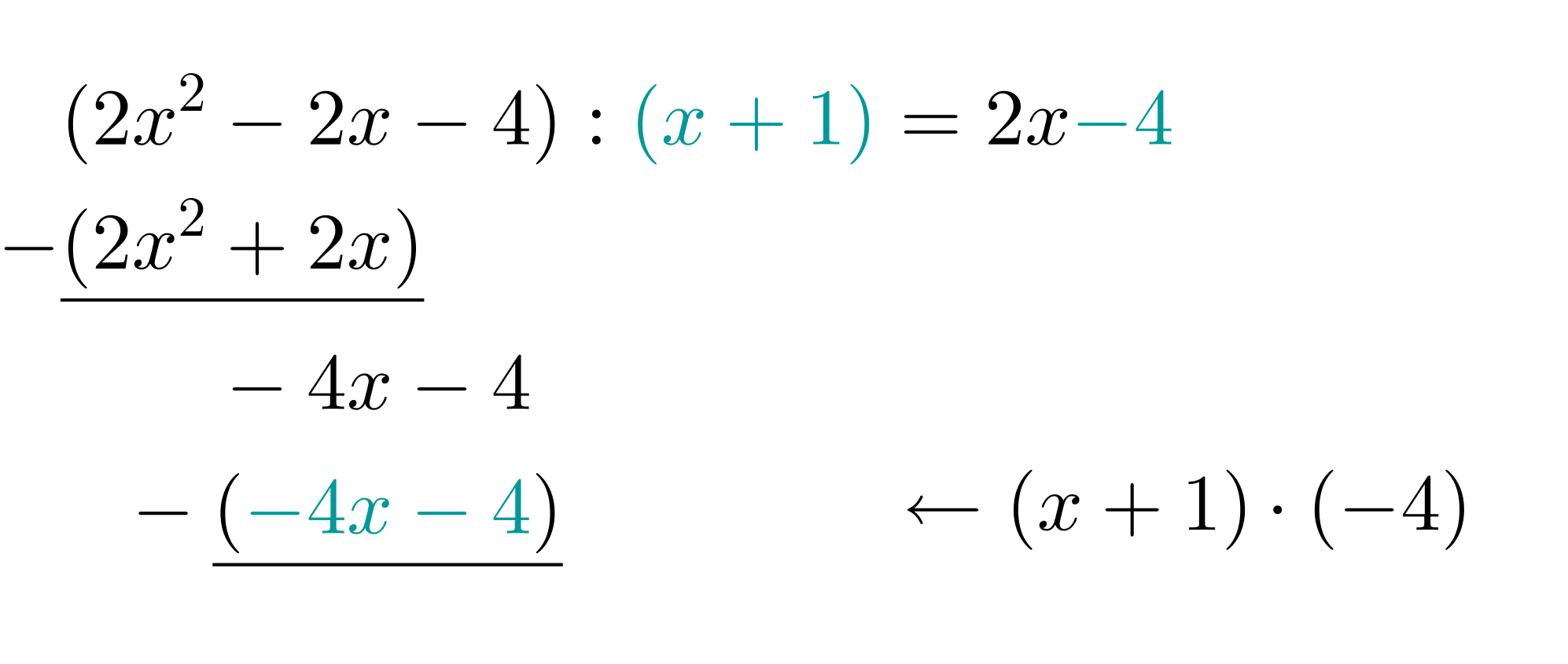
Subtrahieren: Subtrahiere jetzt vom restlichen Dividenden.
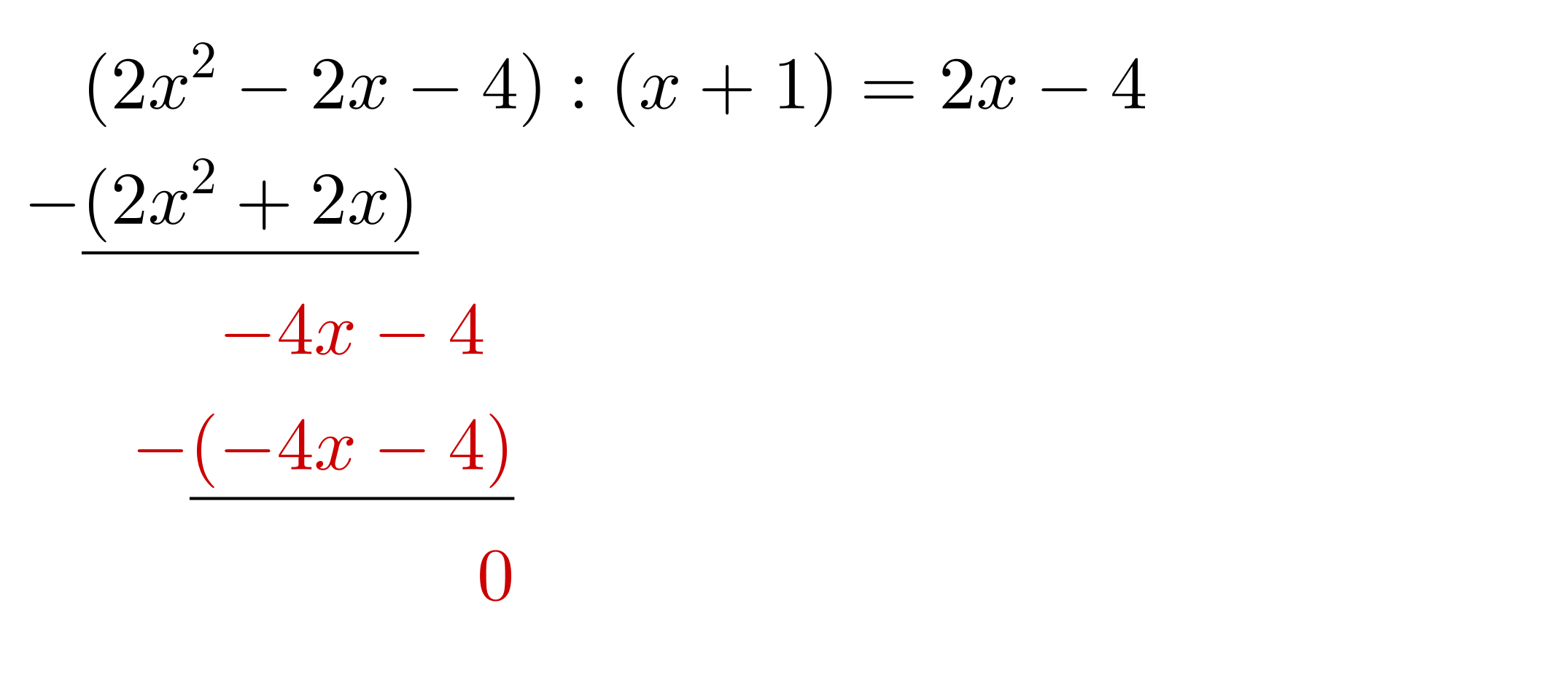
10 Übungsaufgaben zur Polynomdivision
Laden
Laden
Laden
Laden
11 Sonderfall: Exponenten fehlen
Bei Polynomen kann es vorkommen, dass vom höchsten Exponenten aus absteigend nicht alle Exponenten vorkommen.
Das kann uns von der Division von Polynomen aber nicht abhalten! Die fehlenden Monome können wir ergänzen, indem wir diese mal nehmen. So wird aus: .
Da gilt, wird somit auch nicht der Wert des Polynoms verändert.
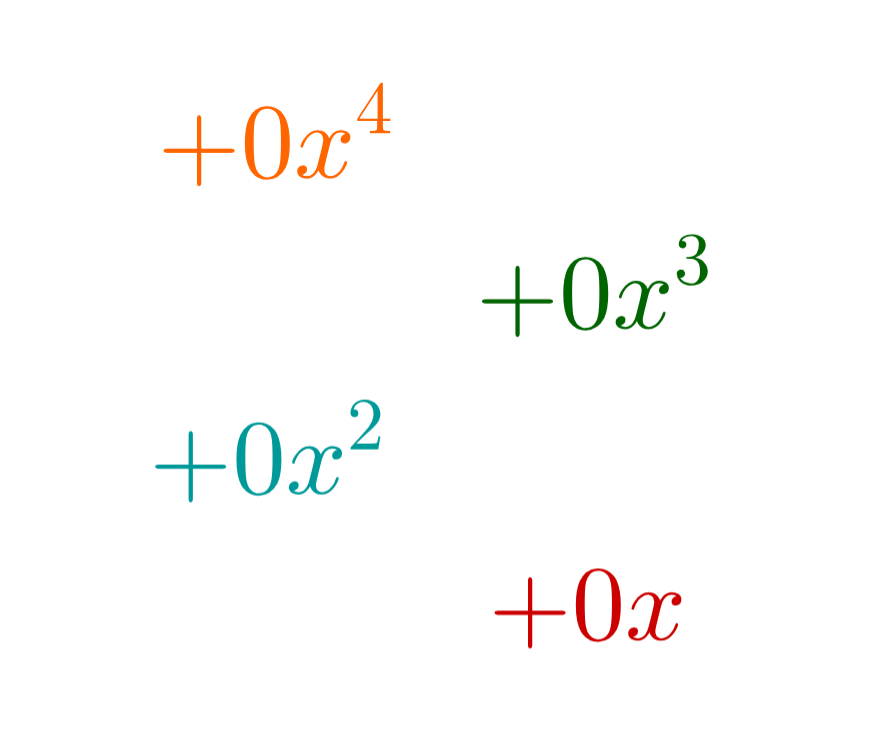
Führen wir die folgende Polynomdivision durch: .
Vorbereitung zur Polynomdivision
Zunächst müssen wir prüfen, ob der Dividend und der Divisor geordnet sind. Das ist hier der Fall, also müssen wir nichts umsortieren.
Im Dividendenpolynom fehlt das Monom zweiten Grades. Addiere also im Dividendenpolynom, damit du das Verfahren der Polynomdivision wie gewohnt anwenden kannst.
Wir berechnen nun: .
Durchführung der Polynomdivision
Gehe bei der Polynomdivision nach dem gleichen Schema vor, wie auf der Kursseite Polynomdivision (2/2) beschrieben.

12 Übungsaufgaben
Aufgaben zur "normalen" Polynomdivision und dem ersten Sonderfall.
Laden
Laden
Laden
13 Sonderfall: Division mit Rest
Nicht immer geht eine Division ohne Rest auf. Du kennst das bereits, wenn du zum Beispiel rechnen möchtest. Du erhältst Rest . Wenn du den Rest durch den Dividenden teilst, bekommst du so:
.
Dieses Vorgehen wenden wir nun auf die Polynomdivision an.
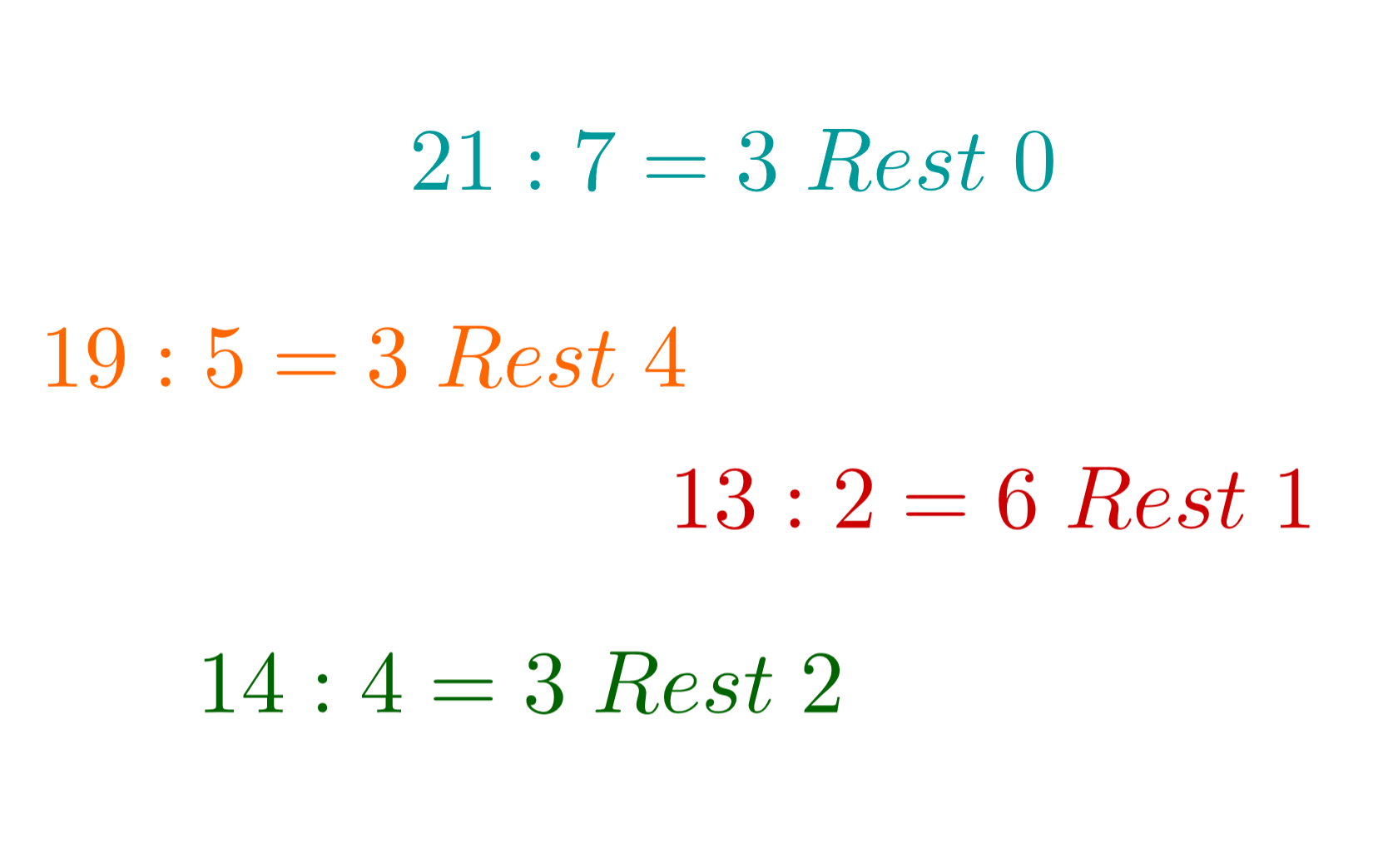
Berechne hierfür:
Vorbereitung zur Polynomdivision
Zunächst müssen wir prüfen, ob der Dividend und der Divisor geordnet sind. Das ist hier der Fall. Also haben wir in der Vorbereitung nichts zu tun.
Durchführung der Polynomdivision
Gehe bei der Polynomdivision nach dem gleichen Schema vor, wie auf der Kursseite Polynomdivision(2/2) beschrieben.

Ende
ist der erste vorkommende Rest, dessen Grad kleiner ist als der Grad des Divisors . Somit sind wir mit der Polynomdivision fertig und erhalten mit Rest . So wie bei der Division von ganzen Zahlen, können wir den Rest noch umschreiben, indem wir ihn durch den Divisor der Polynomdivision teilen.
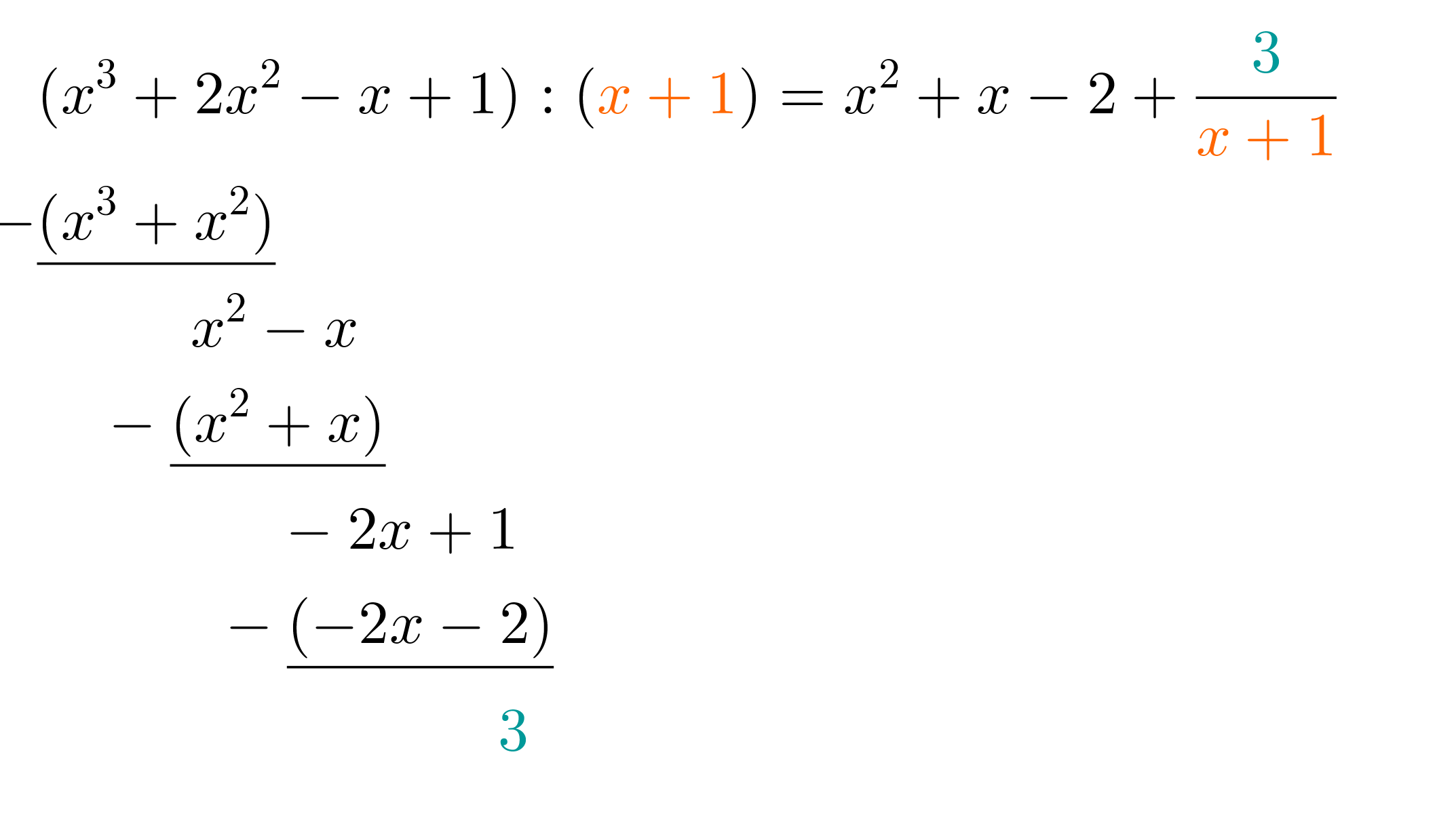
Somit erhalten wir
14 Übungsaufgaben
Hier findest du Aufgaben zu allen Sonderfällen und "normalen" Polynomdivisionen.
Laden
Laden
Laden
Laden
Weitere Übungsaufgaben zur Polynomdivision auch mit Anwendungen findest du im Aufgabenorder zur Polynomdivision.
15 Polynomdivision zur Nullstellenbestimmung
Sind für eine Polynomfunktion vom Grad bereits Nullstellen bekannt (z.B. durch Raten), kannst du die Funktion durch eine Polynomdivision vereinfachen, sodass weitere Nullstellen leichter (z.B. mit der Mitternachtsformel) berechnet werden können.
Dabei kannst du folgendermaßen vorgehen:
1. Schritt: Errate eine Nullstelle durch systematisches Probieren.
2. Schritt: Teile die Ausgangsfunktion durch den zur Nullstelle gehörigen Linearfaktor .
3. Schritt: Überprüfe, ob du die Nullstellen des erhaltenen Polynoms mit einer dir bekannten Formel oder Methode bestimmen kannst. Ist dies nicht der Fall, wiederhole Schritt bis bei diesem Polynom.
4. Schritt: Ermittle die Nullstellen des erhaltenen Polynoms
16 Zusammenfassung
So funktioniert die Polynomdivision:
Vor der Durchführung einer Polynomdivision sind beide Polynome nach fallenden Exponenten zu ordnen.
Eine Polynomdivision vollzieht sich in der Regel in mehreren, jeweils dreigliedrigen Arbeitsschritten:
Division der jeweils ersten Glieder des Dividenden und Divisors. Multiplikation des Divisionsergebnisses mit dem gesamten Divisor. Subtraktion des Multiplikationsergebnisses zur Restbildung.
Eine Polynomdivision geht genau dann auf, wenn das Restpolynom ist.
Eine Polynomdivision endet, wenn ein Restpolynom von kleinerem Grad ist als das Divisorpolynom. Das Ergebnis der Polynomdivision ist dann ein gebrochenrationaler Funktionsterm.

Eine kurze Darstellung des Verfahrens einer Polynomdivision mit Hinweisen auf Anwendungen findest du im Artikel Polynomdivision.
