Aufgaben zu wichtigen Begriffen rund um Funktionen
- 1
Lies aus dem Graphen die Nullstelle ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
- 2
Zeichne anhand der gegebenen Wertetabelle den zugehörigen Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Zeichne die fünf gegebenen Punkte in ein Koordinatensystem und ziehe eine Gerade durch die Punkte.
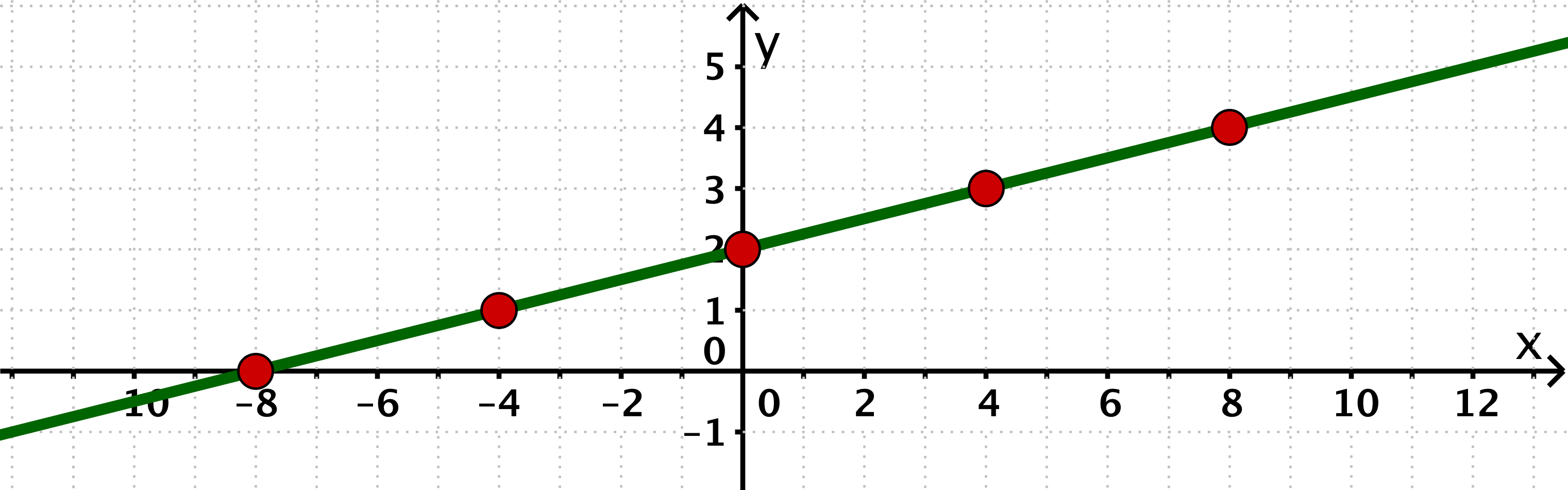
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Zeichne die vier gegebenen Punkte in ein Koordinatensystem und ziehe eine Gerade durch die Punkte.
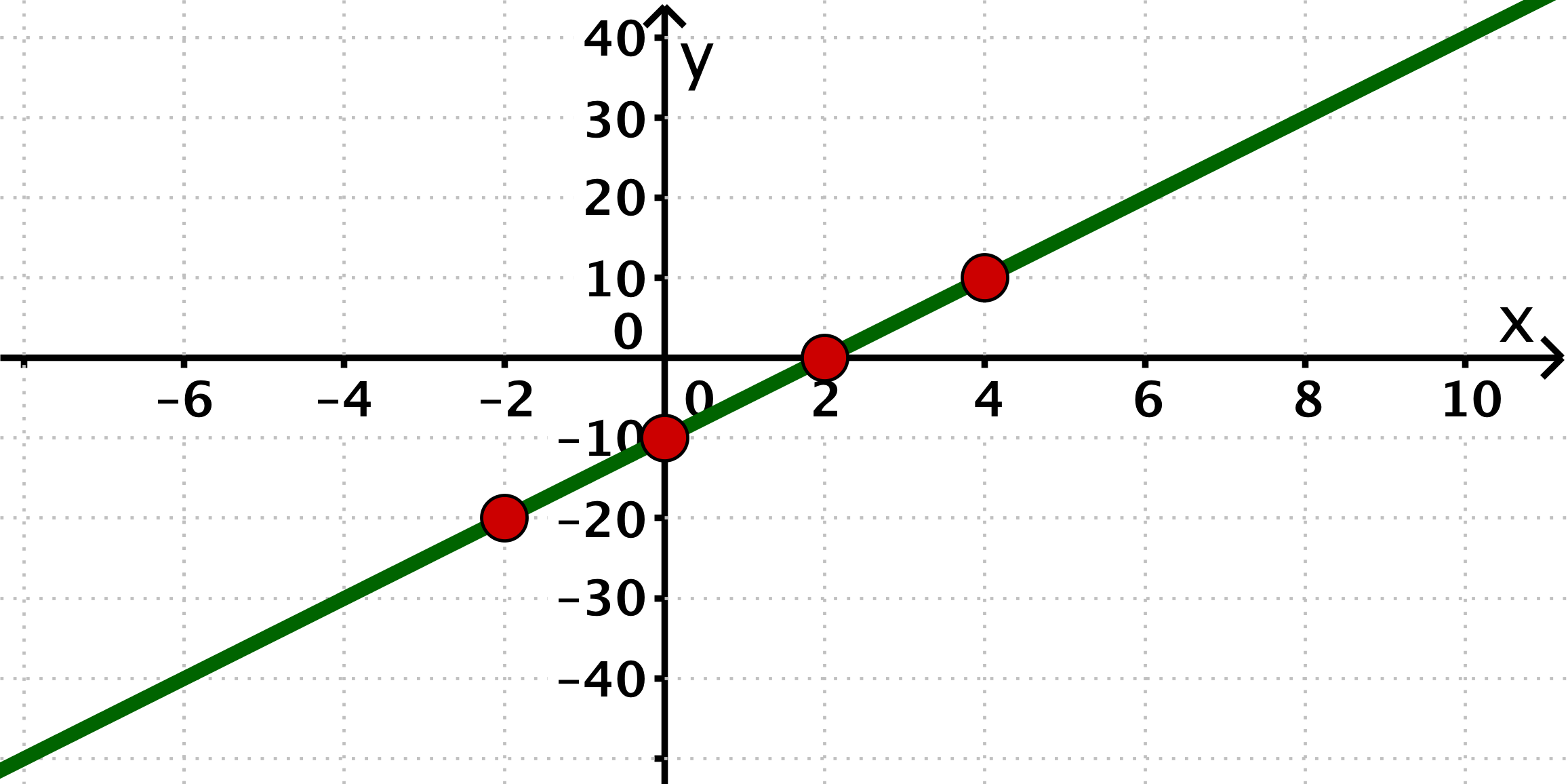
Hast du eine Frage oder Feedback?
- 3
Zeichne die Graphen folgender Geraden mit dem Schnittpunkt mit der y-Achse und dem Steigungsdreieck. Berechne den Schnittpunkt mit der x-Achse und überprüfe das Ergebnis anhand des Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
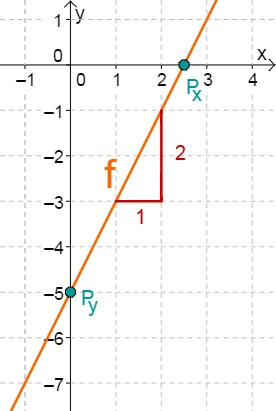
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
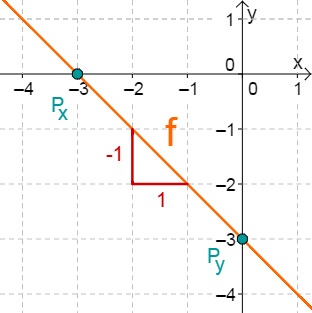
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
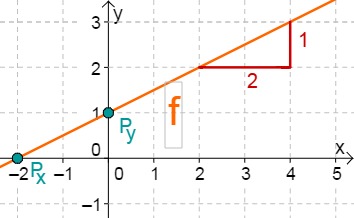
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
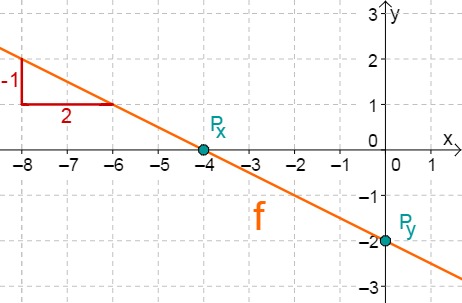
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
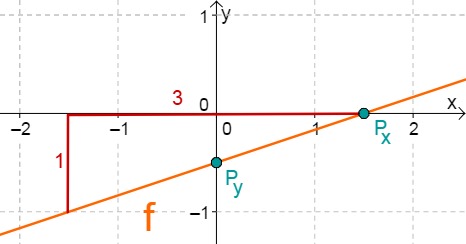
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
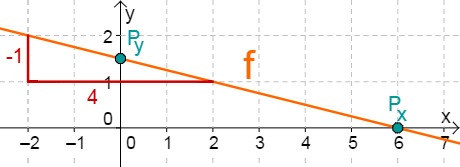
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
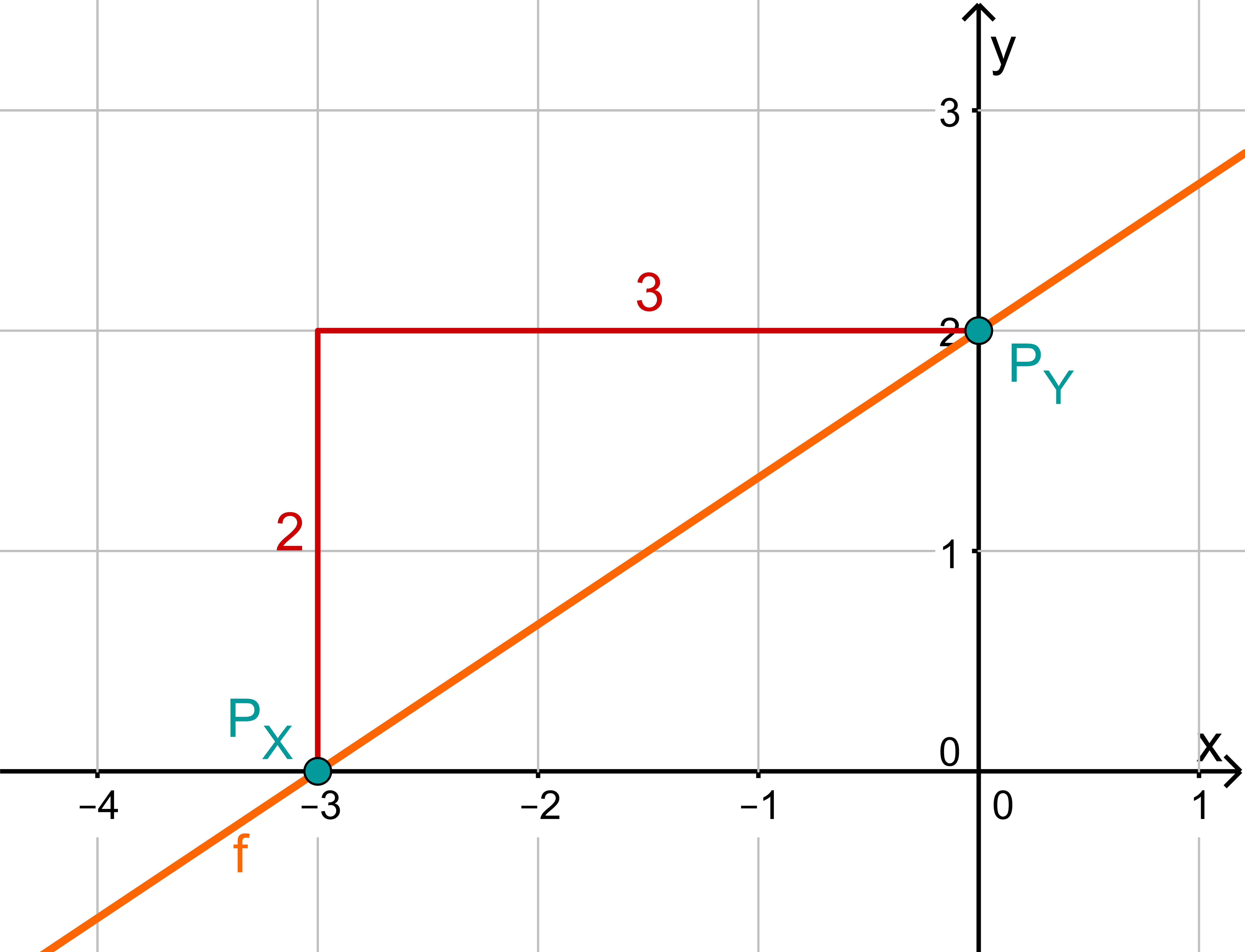
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
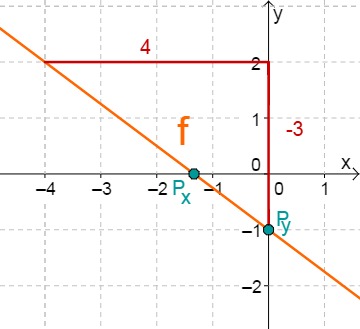
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
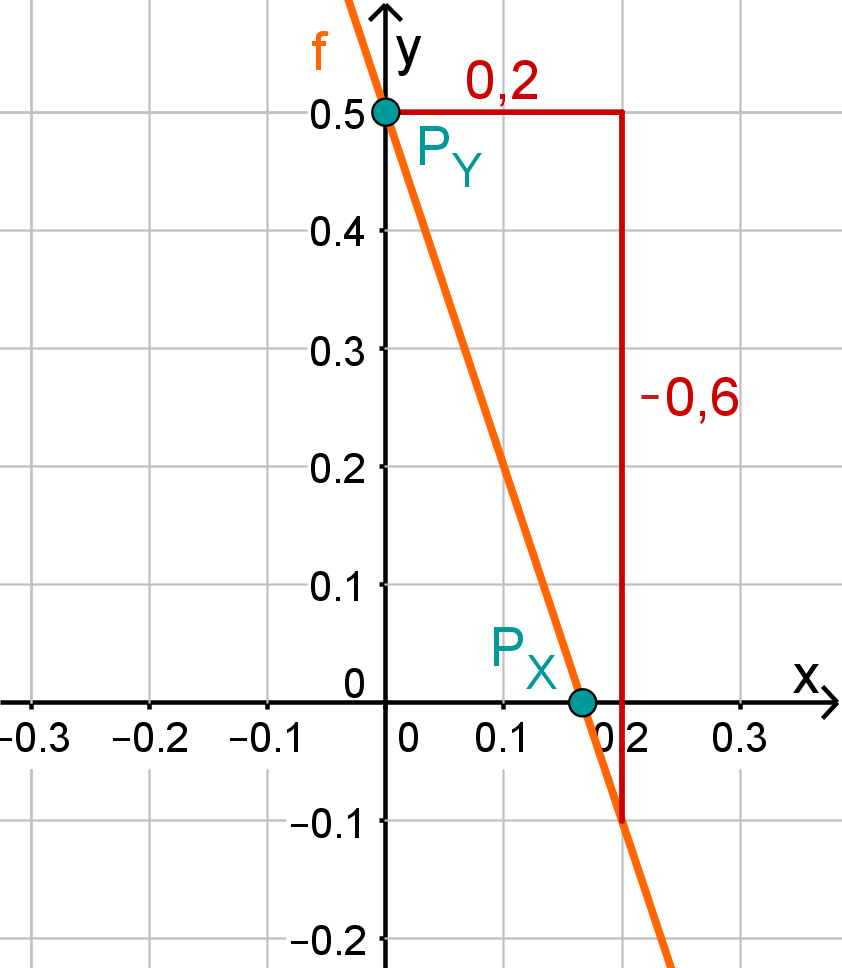
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
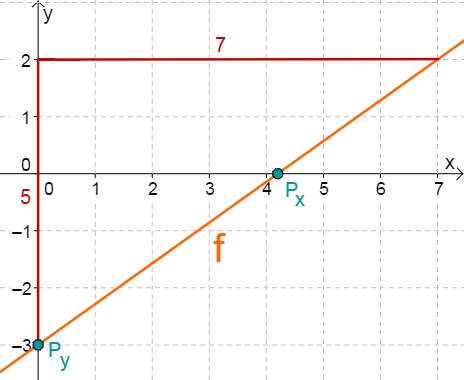
Hast du eine Frage oder Feedback?
- 4
Du fährst mit dem Fahrrad durch die Stadt. Eine App in deinem Handy misst alle 2 Minuten deine aktuelle Geschwindigkeit.
Beschreibe deine Fahrt, zum Beispiel, indem du erst einen Graphen zeichnest und diesen dann deutest. Was könnten Gründe für die jeweiligen Geschwindigkeiten sein?
Minuten nach Fahrtbeginn
0
2
4
6
8
10
12
14
16
18
20
aktuelle Geschwindigkeit (km/h)
0
5
5
0
10
5
5
2
2
0
0
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graphen mit einer Wertetabelle zeichnen
Graph zeichnen
Trage die Punkte aus der Wertetabelle in ein Koordinatensystem ein:
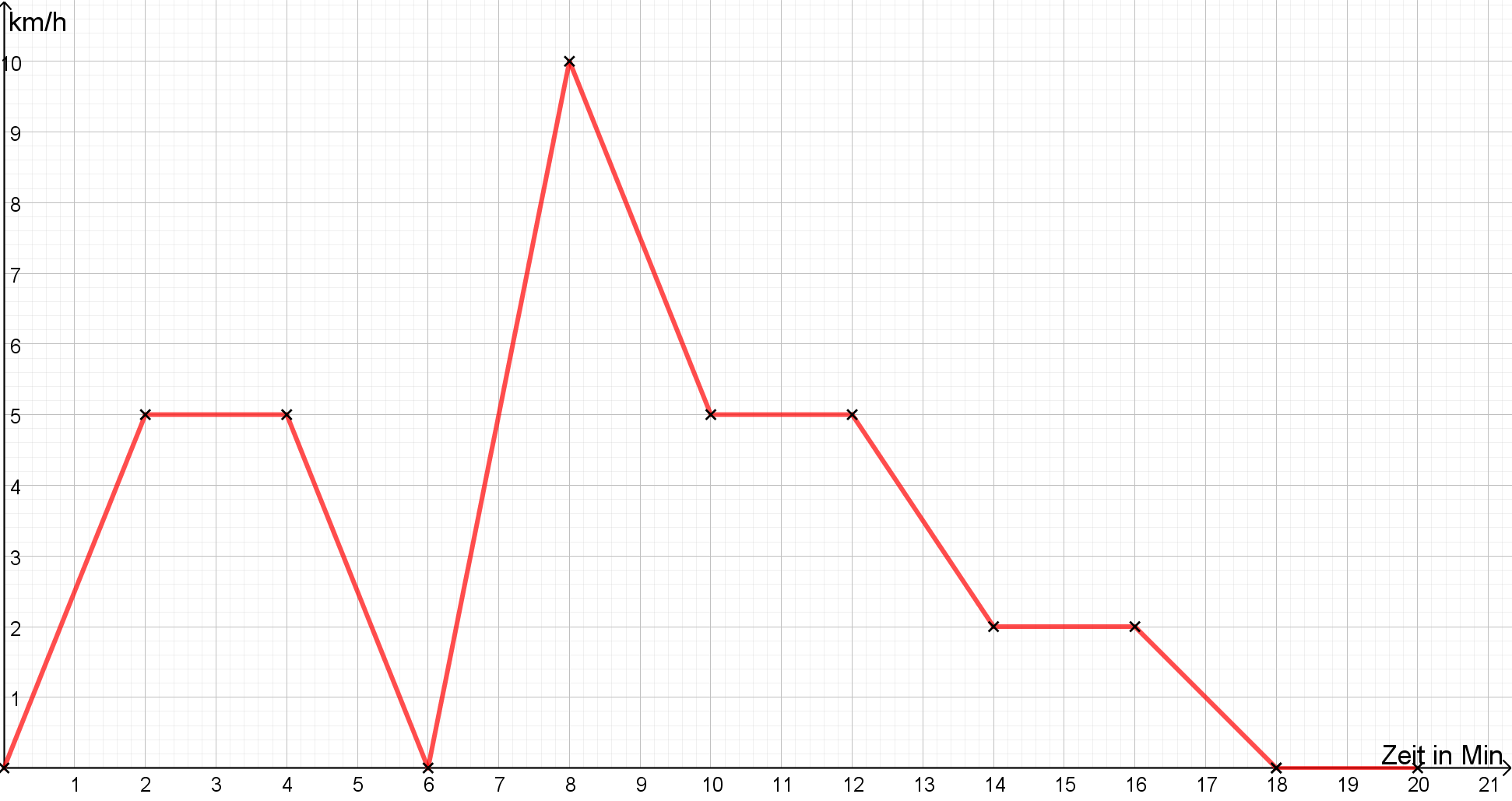
Graph/Tabelle beschreiben
Zunächst beschleunigst du und fährst dann für längere Zeit mit 5 km/h.
Dann bremst du und stehst während Minute 6.
Danach beschleunigst du sehr stark auf 10 km/h.
Anschließend fährst du erneut längere Zeit mit 5 km/h.
Während der 14. und 16. Minute fährst du langsamer, mit 2 km/h.
Nach der 18. Minute stehst du.
Deutung der Werte
Vermutlich fährst du auf geraden Strecken sehr bequem mit 5 km/h.
In der 6. Minute könntest du an einer Ampel stehen oder nochmal angehalten haben, um kurz etwas nachzusehen.
Danach geht es bergab, weshalb du sehr schnell fahren kannst.
Während du 2 km/h fährst, könnte es sein, dass du einen Berg hinauf fährst oder mehr Verkehr herrscht.
Vermutlich bist du nach 18 Minuten am Ziel angekommen.
Zeichne zuerst den Graphen oder stelle ihn dir vor und deute dann die Werte.
- 5
Bestimme von folgenden Geraden die Schnittpunkte mit den Koordinatenachsen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Klammer auflösen
Um eine allgemeine Geradengleichung zu erhalten, multipliziere die Klammer aus.
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein und löse nach auf.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Gleichung umstellen
Um eine allgemeine Geradengleichung zu erhalten, vertausche auf der rechten Seite beide Elemente.
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
- 6
Bestimmung von Schnittpunkten
Im Koordinatensystem sind drei Geraden eingezeichnet. Lies die Schnittpunkte aus der Abbildung ab und gib sie nacheinander in das Eingabefeld ein.
Punkte können in dieser Form eingegeben werden: "(-2|0,5)"
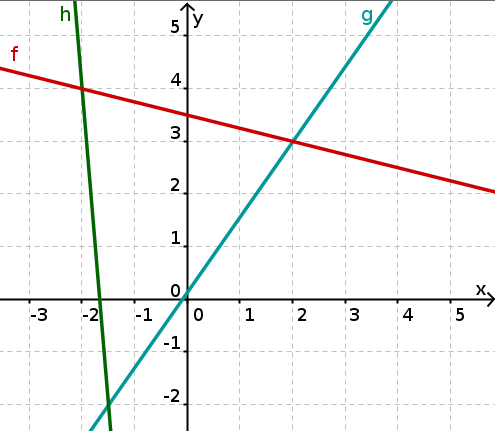
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineares Gleichungssystem
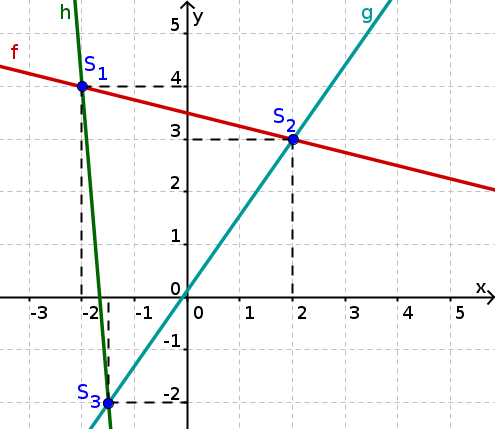
Schnittpunkte ablesen
Im Bild rechts kann man die Koordinaten der drei Punkte ungefähr bestimmen. Diese lauten:
- 7
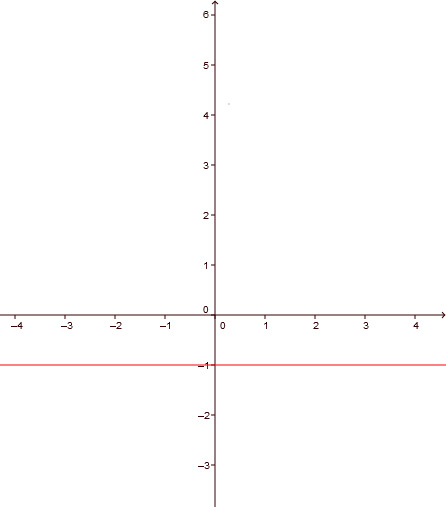
Beschreibe mit Worten die Lage der Geraden mit der Gleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Beschreibung von Geradengleichungen
Es handelt sich hier um eine konstante Funktion, d.h. die Funktion hängt nicht von ab. Jeder der -Werte hat den -Wert .Die Gleichung beschreibt eine Gerade, die eine Paralelle zur x-Achse ist, und die 1 unterhalb der x-Achse liegt.
beschreibt also eine Gerade mit Steigung durch den Punkt .
So sieht der Graph aus:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Beschreibung von Geradengleichungen
Forme um, sodass alleine auf der einen Seite des Gleichheitszeichen steht.
Lese die Steigung und den y-Achsenabschnitt ab.
Die Gleichung beschreibt eine Gerade mit der Steigung und dem y-Achsenabschitt (Sie geht durch den Punkt ) , also die Winkelhalbierende des II und IV Quadranten um nach unten verschoben.
So sieht der Graph aus:
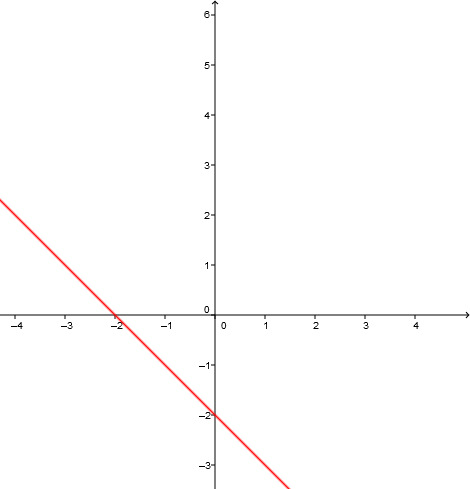
Hast du eine Frage oder Feedback?
- 8
Lies aus dem Graphen den y-Achsenabschnitt ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
- 9
Forme die Gleichung so um, dass sie die Form hat.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
↓ Der Bruch auf der rechten Seite fällt weg da .
↓ Linke und rechte Seite vertauschen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
↓ Beachte: Auf der rechten Seite der Gleichung wird jedes Element der Subtraktion mit multipliziert.
Die einzelnen Multiplikationen:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
↓ Die Klammer ausmultiplizieren.
Hast du eine Frage oder Feedback?
- 10
Die folgende Wertetabelle enthält direktproportionale Wertepaare. Berechne die fehlenden Werte und trage die Wertepaare in ein Gitternetz ein.
Menge in Liter
4
6
8
Preis in €
6
12
16,5
Für diese Aufgabe benötigst Du folgendes Grundwissen: Direkte Proportionalität
Graphisch Lösen
Zeichne die beiden Wertepaare und in ein Koordinatensystem und zeichne die Gerade durch die beiden Punkte. Nun kannst du die anderen Werte ablesen.
-Achse: entspricht -Achse: entspricht
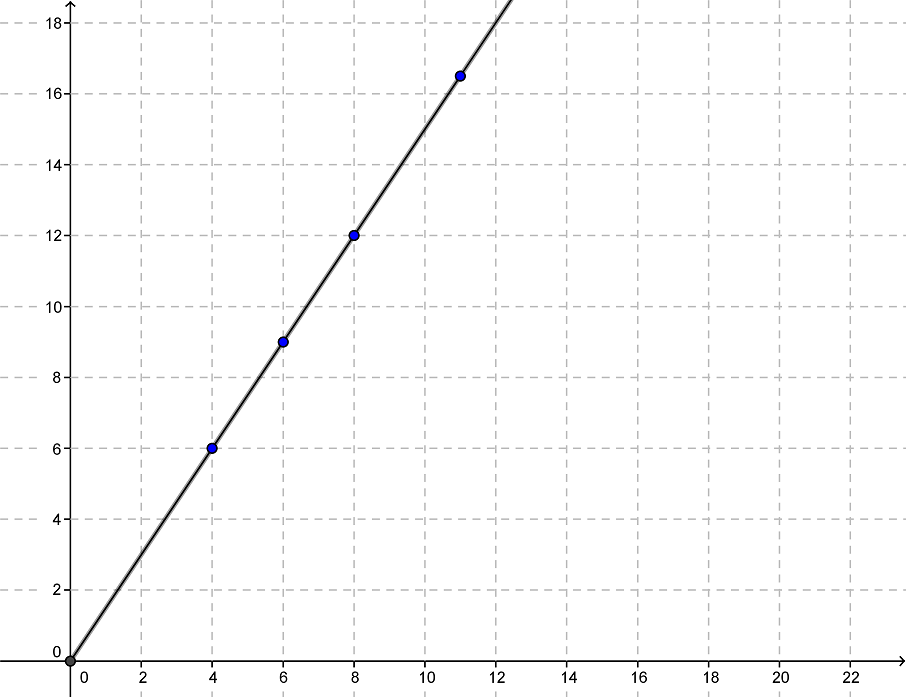
Menge in Liter
4
6
8
Preis in €
6
12
16,5
Rechnerische Lösung
Verwende die Proportionalitätskonstante, um den Preis pro Liter zu bestimmen. Dividiere dazu bei einem Wertepaar den Preis durch die Literanzahl:
€ €/
Ein Liter kostet also €
Berechne damit den Preis für :
€/ €
kosten also €.
Beim letzen Wertepaar weißt du, dass € bezahlt wurden. Teile diese Zahl durch den Literpreis von €/
€ €
Für € bekommt man also .
Hinweis: Man kann diese Aufgabe auch anders lösen, zum Beispiel mit dem Dreisatz. Wenn du einen anderen, richtigen Lösungsweg hast, kannst du ihn hier gerne noch ergänzen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
































