Gegenseitige Lage von zwei Kugeln

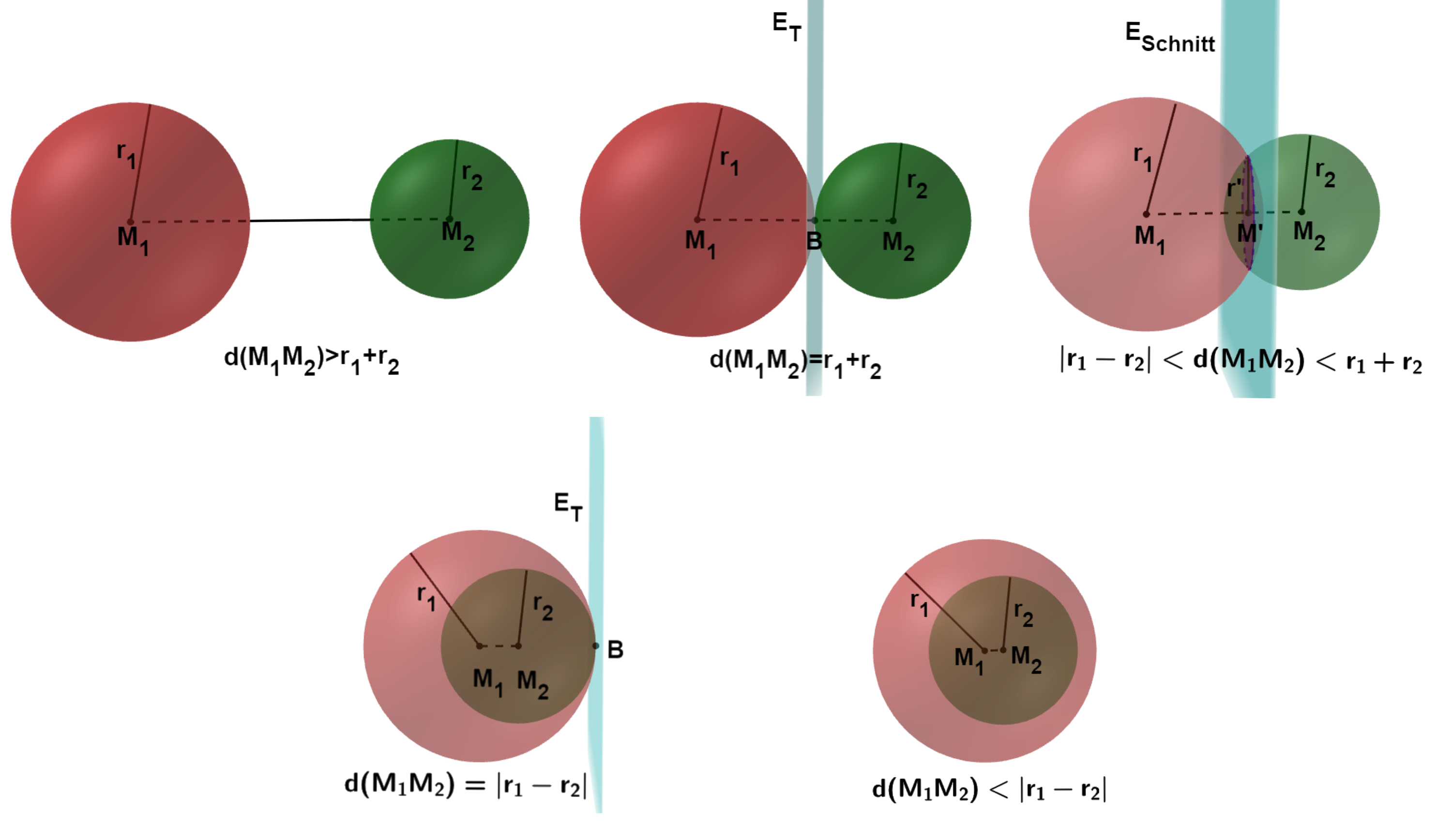
Es wird die Lage zweier Kugeln $K_{1}$ und $K_{2}$ zueinander untersucht.

Dabei treten fünf Fälle auf:

die Kugeln schneiden sich nicht (oberes linkes Bild)
die Kugeln berühren sich in genau einem äußeren Punkt $B$ . Die Kugeln haben eine gemeinsame Tangentialebene (oberes mittleres Bild).
die beiden Kugeln schneiden sich in einem Schnittkreis (oberes rechtes Bild)
die Kugeln liegen ineinander und berühren sich innen in einem Punkt $B$ . Die Kugeln haben eine gemeinsame Tangentialebene (unteres linkes Bild).
die Kugeln liegen ineinander und berühren sich nicht (unteres rechtes Bild)

Allgemeines Vorgehen

Die Kugel $K_{1}$ ist gegeben durch ihren Mittelpunkt $M_{1}$ und den Radius $r_{1}$ .

Die Kugel $K_{2}$ ist gegeben durch ihren Mittelpunkt $M_{2}$ und den Radius $r_{2}$ .

Die Ermittlung der Lage von zwei Kugeln erfolgt über die Berechnung des Abstandes der beiden Kugelmittelpunkte $M_{1}$ und $M_{2}$ .

Nun sind fünf Fälle möglich:

$d (M_{1}, M_{2}) > r_{1} + r_{2}$ ; die Kugeln schneiden sich nicht
$d (M_{1}, M_{2}) = r_{1} + r_{2}$ ; die Kugeln berühren sich in genau einem Punkt $B$ . Die Kugeln haben eine gemeinsame Tangentialebene.
$| r_{1} - r_{2} | < d (M_{1}, M_{2}) < r_{1} + r_{2}$ ; die beiden Kugeln schneiden sich in einem Schnittkreis
$d (M_{1}, M_{2}) = | r_{1} - r_{2} |$ ; die Kugeln liegen ineinander und berühren sich innen in einem Punkt $B$ . Die Kugeln haben eine gemeinsame Tangentialebene.
$d (M_{1}, M_{2}) < | r_{1} - r_{2} |$ ; die Kugeln liegen ineinander und berühren sich nicht

Beispiel 1

Die Kugel $K_{1}$ ist gegeben durch ihren Mittelpunkt $M_{1} (8 | 0 | 0)$ und den Radius $r_{1} = 3$ .

Die Kugel $K_{2}$ ist gegeben durch ihren Mittelpunkt $M_{2} (0 | 0 | 0)$ und den Radius $r_{2} = 2$ .

Berechne den Abstand der beiden Mittelpunkte und vergleiche mit der Summe der beiden Radien.

$d (M_{1}, M_{2}) = 8$ ; $r_{1} + r_{2} = 3 + 2 = 5$

Hier gilt $d (M_{1}, M_{2}) = 8 > r_{1} + r_{2} = 5$ , d.h. die Kugeln schneiden sich nicht.

Beispiel 2

Die Kugel $K_{1}$ ist gegeben durch ihren Mittelpunkt $M_{1} (5 | 0 | 0)$ und den Radius $r_{1} = 3$ .

Die Kugel $K_{2}$ ist gegeben durch ihren Mittelpunkt $M_{2} (0 | 0 | 0)$ und den Radius $r_{2} = 2$ .

Berechne den Abstand der beiden Mittelpunkte und vergleiche mit der Summe der beiden Radien.

$d (M_{1}, M_{2}) = 5$ ; $r_{1} + r_{2} = 3 + 2 = 5$

Hier gilt $d (M_{1}, M_{2}) = r_{1} + r_{2} = 5$ , d.h. die Kugeln berühren sich außen in genau einem Punkt $B$ . Die Kugeln haben eine gemeinsame Tangentialebene.

Siehe auch: Zwei Kugeln mit gemeinsamen äußeren Berührpunkt

Beispiel 3

Die Kugel $K_{1}$ ist gegeben durch ihren Mittelpunkt $M_{1} (4 | 0 | 0)$ und den Radius $r_{1} = 3$ .

Die Kugel $K_{2}$ ist gegeben durch ihren Mittelpunkt $M_{2} (0 | 0 | 0)$ und den Radius $r_{2} = 2$ .

Berechne den Abstand der beiden Mittelpunkte und vergleiche mit der Summe der beiden Radien.

$d (M_{1}, M_{2}) = 4$ ; $r_{1} + r_{2} = 3 + 2 = 5$ ; $| r_{1} - r_{2} | = | 3 - 2 | = 1$

Hier gilt $| r_{1} - r_{2} | = 1 < d (M_{1}, M_{2}) = 4 < r_{1} + r_{2} = 5$ , d.h. die beiden Kugeln schneiden sich in einem Schnittkreis.

Siehe auch: Zwei sich schneidende Kugeln

Beispiel 4

Die Kugel $K_{1}$ ist gegeben durch ihren Mittelpunkt $M_{1} (1 | 0 | 0)$ und den Radius $r_{1} = 3$ .

Die Kugel $K_{2}$ ist gegeben durch ihren Mittelpunkt $M_{2} (0 | 0 | 0)$ und den Radius $r_{2} = 2$ .

Berechne den Abstand der beiden Mittelpunkte und vergleiche mit der Summe der beiden Radien.

$d (M_{1}, M_{2}) = 1$ ; $| r_{1} - r_{2} | = | 3 - 2 | = 1$

Hier gilt $d (M_{1}, M_{2}) = | r_{1} - r_{2} | = 1$ , d.h. die Kugeln liegen ineinander und berühren sich innen in einem Punkt $B$ .

Siehe auch: Zwei Kugeln mit gemeinsamen inneren Berührpunkt

Beispiel 5

Die Kugel $K_{1}$ ist gegeben durch ihren Mittelpunkt $M_{1} (0,5 | 0 | 0)$ und den Radius $r_{1} = 3$ .

Die Kugel $K_{2}$ ist gegeben durch ihren Mittelpunkt $M_{2} (0 | 0 | 0)$ und den Radius $r_{2} = 2$ .

Berechne den Abstand der beiden Mittelpunkte und vergleiche mit der Summe der beiden Radien.

$d (M_{1}, M_{2}) = 0,5$ ; $| r_{1} - r_{2} | = | 3 - 2 | = 1$

Hier gilt $d (M_{1}, M_{2}) = 0,5 < | r_{1} - r_{2} | = 1$ , d.h. die Kugeln liegen ineinander und berühren sich nicht.

Übungsaufgaben

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?