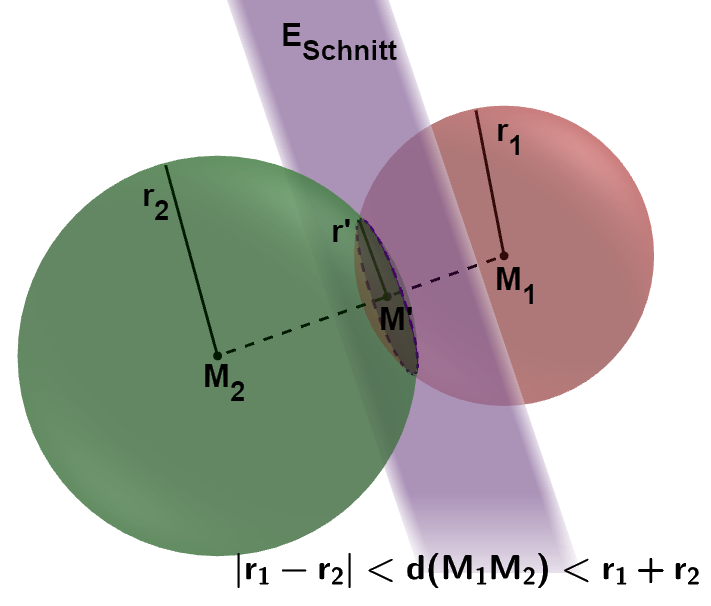
Ist der Betrag der Differenz der beiden Kugelradien kleiner als der Abstand der beiden Kugelmittelpunkte und dieser wiederum kleiner als die Summe der beiden Kugelradien, dann schneiden sich die Kugeln in einem Schnittkreis mit dem Mittelpunkt und dem Radius .
Der Schnittkreis liegt in der Ebene .
Schnittbedingung:
Gesucht sind die Gleichung der Schnittebene , und .
Allgemeines Vorgehen
Die Kugel ist gegeben durch ihren Mittelpunkt und den Radius .
Die Kugel ist gegeben durch ihren Mittelpunkt und den Radius .
Die Ermittlung der Lage von zwei Kugeln erfolgt über die Berechnung des Abstandes der beiden Kugelmittelpunkte und .
Berechne den Vektor und dann seinen Betrag.
Vergleiche mit dem Betrag der Differenz der beiden Kugelradien und der Summe der beiden Kugelradien.
Wenn die Bedingung erfüllt ist, dann schneiden sich die beiden Kugeln in einem Schnittkreis.
Berechnung der Schnittkreisebene
Wandle von beiden Kugeln die Vektorgleichung in eine Koordinatendarstellung um. Die Differenz der beiden Koordinatengleichungen liefert die Gleichung der gesuchten Schnittebene .
Berechnung des Mittelpunkt
Erstelle die Gleichung der Lotgeraden durch den Mittelpunkt auf die Ebene .
Verwende als Aufpunkt den Mittelpunkt und als Richtungsvektor den Normalenvektor der Ebene :
Berechne den Mittelpunkt , indem du die Lotgerade mit der Ebene schneidest.

Berechnung des Schnittkreisradius
(In der Abbildung ist nur die Kugel dargestellt.)
Den Schnittkreisradius kannst du mithilfe des Satzes von Pythagoras berechnen. Der Abstand der Ebene vom Mittelpunkt ist der Betrag des Vektors und der Kugelradius von ist .
Es gilt dann:

Beispiel
Gegeben sind die Kugeln und
Zeige, dass die beiden Kugeln sich schneiden und gib die Gleichung der Schnittebene , den Mittelpunkt des Schnittkreises und den Schnittkreisradius an.
Lagebeziehung der beiden Kugeln
Gegeben sind die beiden Kugelradien: und
Berechne:
Zu 2. Berechne den Vektor
Berechne 2
Setze die berechneten Werte in die Schnittpunktsbedingung ein:
Die Schnittpunktsbedingung ist erfüllt, d.h. die beiden Kugeln schneiden sich.
Berechnung der Schnittkreisebene
Wandle die Kugelgleichung in eine Koordinatengleichung um:
| ↓ | Rechne das Skalarprodukt aus. | ||
| ↓ | Berechne die Quadrate und vergiss nicht die binomische Formel anzuwenden. | ||
| ↓ | Vereinfache | ||
Die Kugel hat die Koordinatengleichung:
Wandle die Kugelgleichung in eine Koordinatengleichung um:
| ↓ | Rechne das Skalarprodukt aus. | ||
| ↓ | Berechne die Quadrate und vergiss nicht die binomische Formel anzuwenden. | ||
| ↓ | Fasse zusammen. | ||
| ↓ | Vereinfache | ||
Die Kugel hat die Koordinatengleichung:
Schnitt der beiden Kugeln berechnen
Die Kugel ist Gleichung und die Kugel ist Gleichung . Es handelt sich hier um ein Gleichungssystem mit 2 Gleichungen und 3 Variablen.
Berechne die Differenz der beiden Gleichungen.
Antwort: Die Gleichung der Schnittebene lautet .
Berechnung des Mittelpunkt
Erstelle die Gleichung der Lotgeraden durch den Mittelpunkt auf die Ebene .
Verwende als Aufpunkt den Mittelpunkt und als Richtungsvektor den Normalenvektor der Ebene :

oder
Berechne den Mittelpunkt , indem du die Lotgerade mit der Ebene schneidest:
| ↓ | Setze , und ein. | ||
| ↓ | Löse die Klammern auf. | ||
| ↓ | Vereinfache. | ||
| ↓ | Löse nach auf. | ||
Zur Berechnung des Schnittpunktes setzt du in die Gleichung der Lotgeraden ein.
Antwort: Der Mittelpunkt hat die Koordinaten .
Berechnung des Schnittkreisradius
Den Schnittkreisradius kannst du mithilfe des Satzes von Pythagoras berechnen. Der Abstand der Ebene vom Mittelpunkt ist der Betrag des Vektors und der Kugelradius von ist . Es gilt:

Berechne zuerst den Vektor und dann dessen Betrag.
| ↓ | Setze und ein. | ||
| ↓ | Vereinfache. | ||
| ↓ | Vereinfache. | ||
Antwort: Der Radius des Schnittkreises beträgt .
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Kugeln in der analytischen Geometrie
- Tangentialebene an eine Kugel
- Lagebeziehungen zwischen Kugeln und Punkten
- Lagebeziehung zwischen Kugeln und Geraden
- Lagebeziehung zwischen Kugeln und Ebenen
- Kugel und Tangentialkegel
- Gegenseitige Lage von zwei Kugeln
- Zwei Kugeln mit gemeinsamen äußeren Berührpunkt
- Zwei Kugeln mit gemeinsamen inneren Berührpunkt
