Aufgabengruppe I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
Normalparabel
Formen Sie die Funktionsgleichung der Normalparabel in die Scheitelpunktform um und geben Sie den Scheitelpunkt an.
Überprüfen Sie durch Rechnung, ob die Punkte und auf der Normalparabel liegen.
Die Normalparabel schneidet die x-Achse in den Punkten und . Ermitteln Sie rechnerisch die Koordinaten dieser beiden Punkte und geben Sie und an.
Die nach unten geöffnete Normalparabel verläuft durch die Punkte und . Bestimmen Sie rechnerisch die Funktionsgleichung von in der Normalform.
Die nachfolgende Abbildung zeigt den Graphen einer Normalparabel . Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
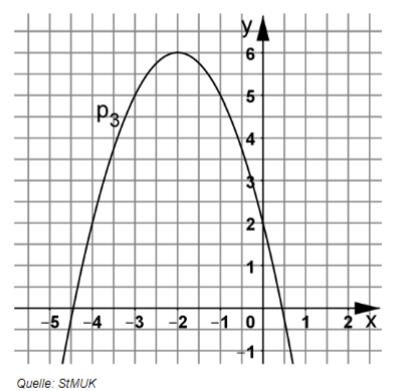
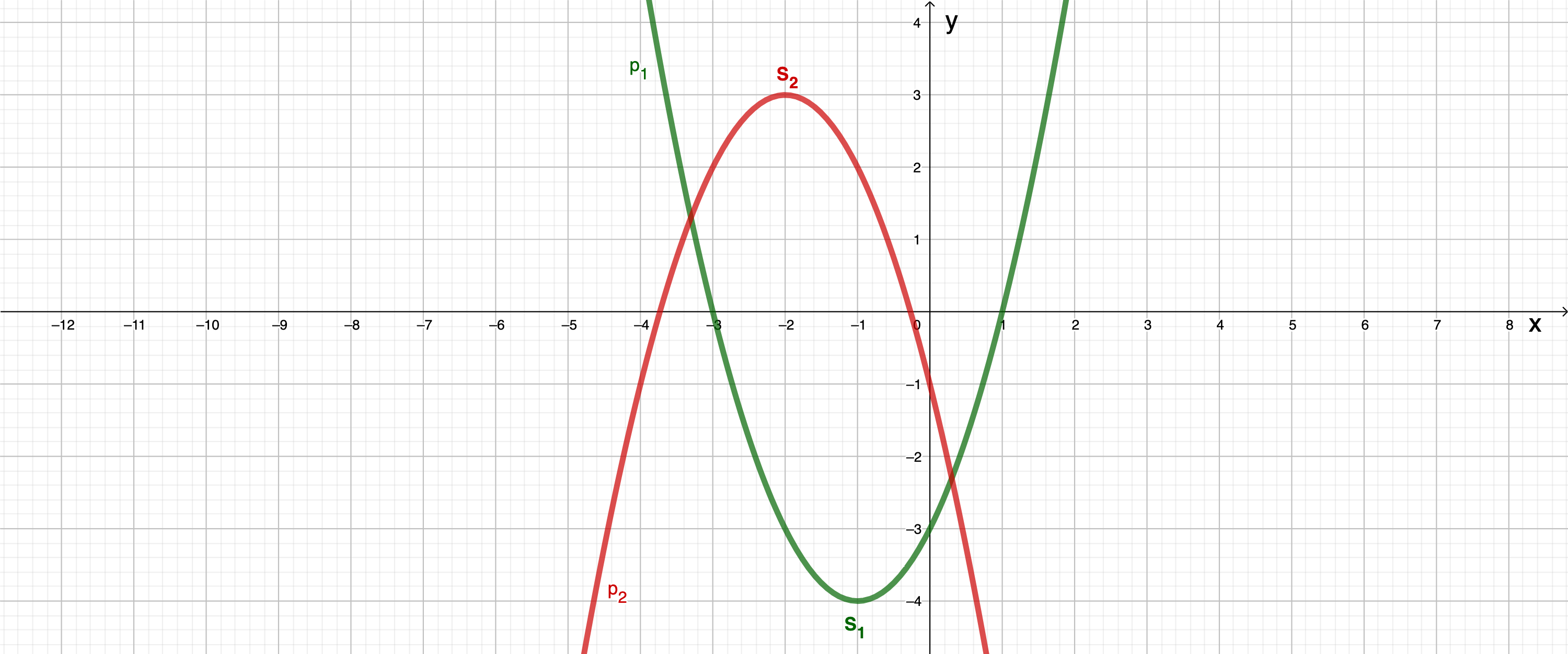
Berechnen Sie die Koordinaten der Schnittpunkte und der Normalparabel
: mit der Geraden und geben Sie und an.
Zeichnen Sie die Graphen der Normalparabeln und in ein Koordinatensystem mit der Längeneinheit 1 cm.
- 2
In einer bayerischen Stadt waren am 01.01.2010 insgesamt 67279 Menschen gemeldet.
Neun Jahre später waren es bereits 81240 Menschen. Berechnen Sie für diesen Zeitraum das durchschnittliche jährliche Bevölkerungswachstum in Prozent.
Die Anzahl der unter 6-jährigen Kinder ging im Zeitraum von zwei Jahren um jährlich 1,3 % auf 3245 Personen zurück. Berechnen Sie die Anzahl der Personen dieser Altersgruppe zu Beginn dieser beiden Jahre.
KinderBerechnen Sie, nach wie vielen Jahren sich die Zahl der Bewohner dieser Stadt verdoppeln würde, wenn man von einem durchschnittlichen jährlichen Zuwachs von 3,75% ausgeht. Runden Sie das Ergebnis auf volle Jahre.
Jahre
- 3
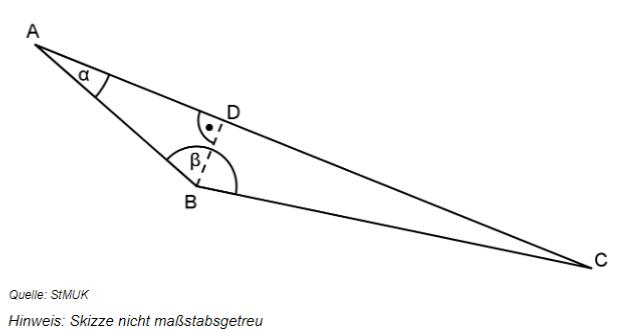
In der folgenden Skizze gilt: ; ; . Berechnen Sie die Länge der Strecke in cm.
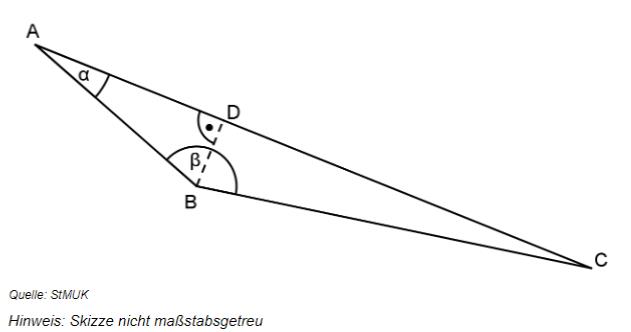
- 4
Vereinfachen Sie den untenstehenden Term soweit wie möglich.
Es gilt:
- 5
Lösen Sie folgende Aufgaben.
Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden , die durch die Punkte und B verläuft.
Die Gerade verläuft durch den Punkt und steht senkrecht auf der Geraden : . Ermitteln Sie rechnerisch die Funktionsgleichung der Geraden .
Zeichnen Sie die Geraden und in ein Koordinatensystem mit der Längeneinheit 1 cm.
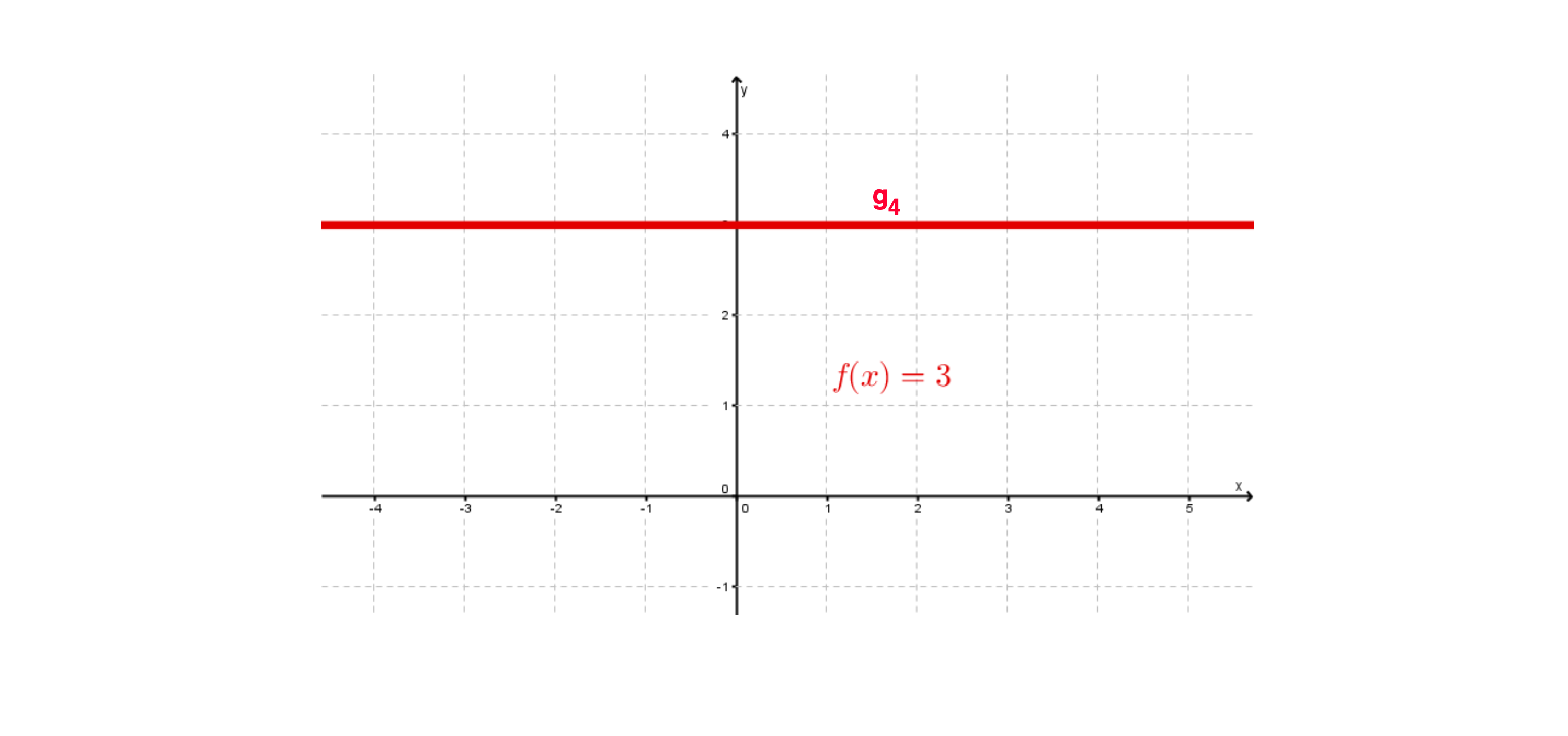
Geben Sie eine mögliche Funktionsgleichung einer Geraden an, die parallel zur
x-Achse verläuft.
Der Punkt liegt auf der Geraden : . Bestimmen Sie die Steigung rechnerisch.
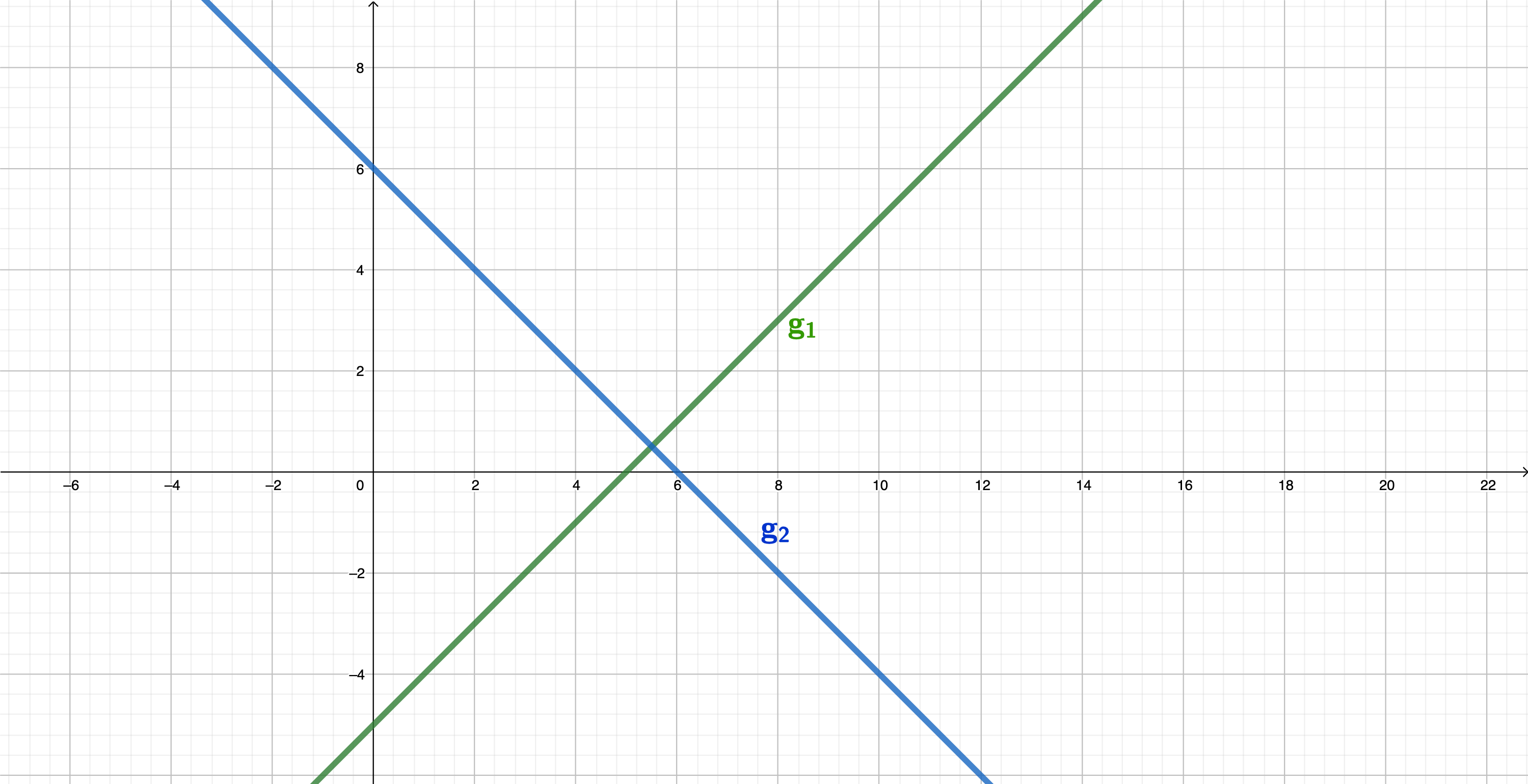
Die Geraden : und : schneiden sich im Punkt Ermitteln Sie rechnerisch die Koordinaten des Schnittpunkts und geben Sie an.
Berechnen Sie die Koordinaten des Schnittpunkts der Geraden mit der
x-Achse und geben Sie an.
- 6
Lösen Sie die folgende Gleichung rechnerisch. Geben Sie die Definitionsmenge und die Lösungsmenge an.
- 7
Für die Herstellung eines goldenen, halbkugelförmigen Schmuckanhängers mit einem Durchmesser von 11 mm verwendet ein Goldschmied das Gold von acht kleineren Kugeln mit einem Durchmesser von jeweils 4,5 mm. Anschließend stellt er aus dem überschüssigen Material eine Goldkugel für ein weiteres Schmuckstück her. Berechnen Sie den Radius dieser neuen Goldkugel.
- 8
Es gilt:
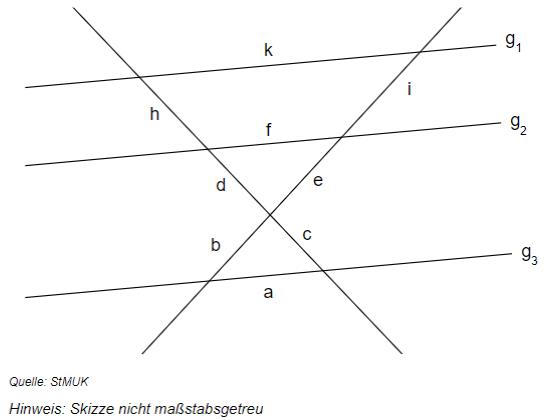
Durch korrektes Ersetzen der Platzhalter sollen richtige Anwendungen der Strahlensätze entstehen. Schreiben Sie die richtigen Gleichungen vollständig auf Ihr Lösungsblatt.
(1)
(2)
(3)
- 9
Folgende Aufgaben sind Anwendungen von binomischen Formeln. Ersetzen Sie die Platzhalter jeweils durch den entsprechenden Term und schreiben Sie die mathematisch richtige Gleichung auf Ihr Lösungsblatt.
(1)
(2)
- 10
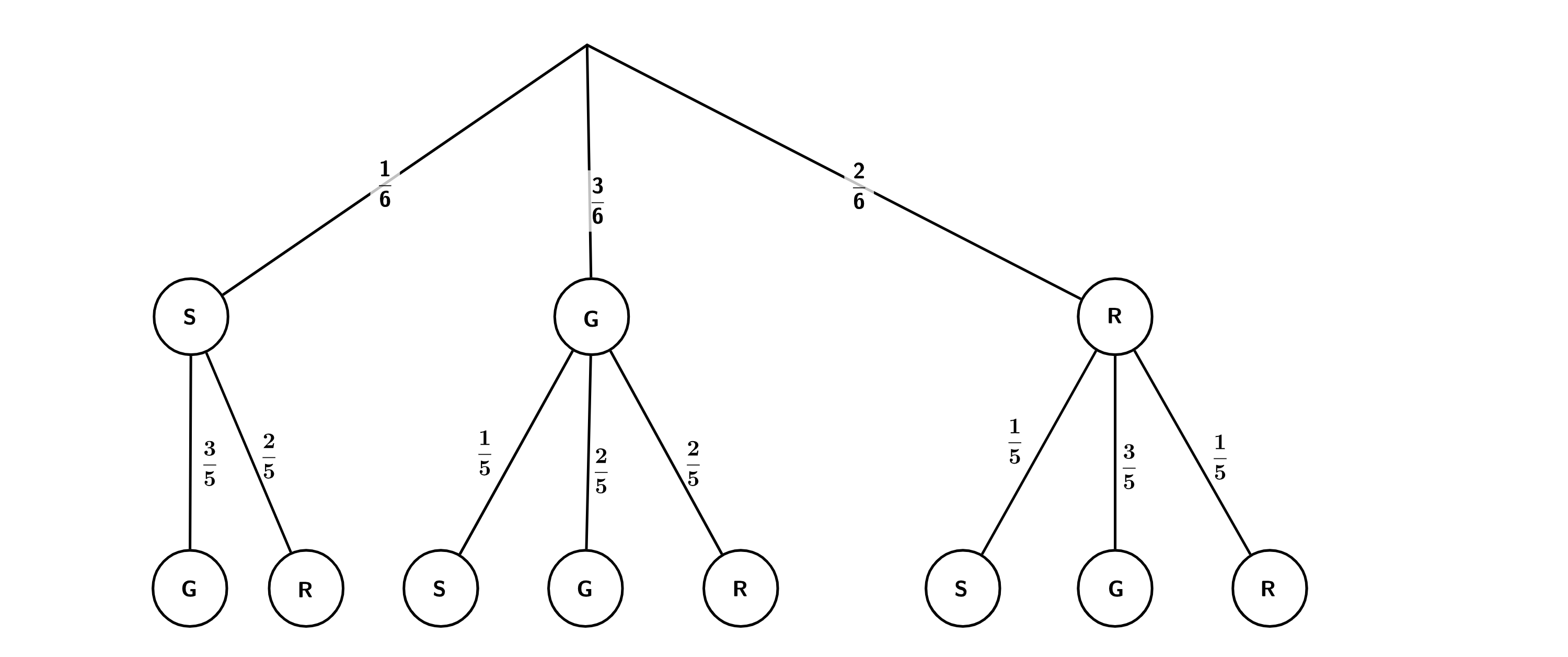
In einem Behälter befinden sich sechs Kugeln, von denen eine Kugel schwarz, drei grün und zwei rot sind. Zwei Mal nacheinander wird eine Kugel zufällig gezogen und nicht zurückgelegt.
Zeichnen Sie ein Baumdiagramm mit den möglichen Ergebnissen und beschriften Sie die Äste mit den entsprechenden Wahrscheinlichkeiten.
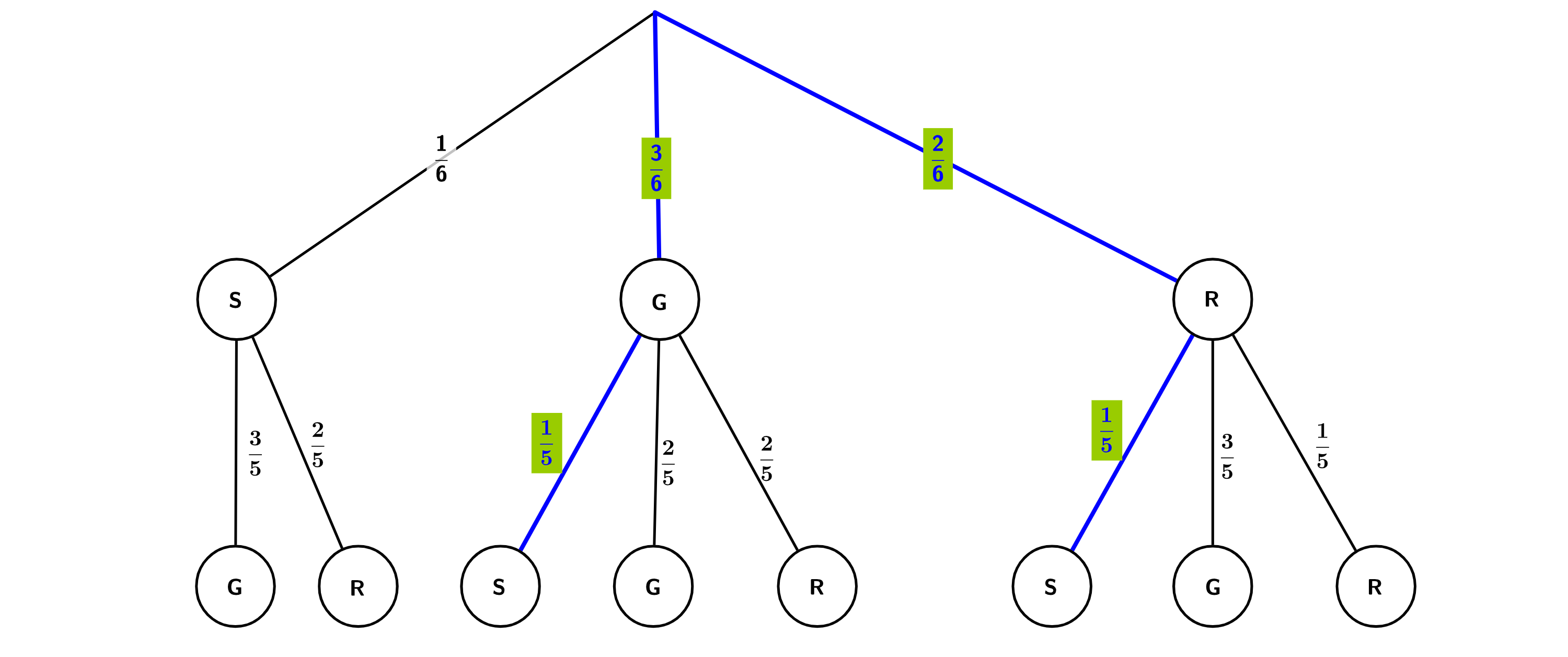
Die zweite gezogene Kugel soll schwarz sein. Bestimmen Sie für dieses Ereignis die Wahrscheinlichkeit in Prozent.
Die höchstmögliche Wahrscheinlichkeit für eine bestimmte Farbkombination, ohne Beachtung der Reihenfolge, beträgt beim im Vortext beschriebenen Zufallsexperiment 40 Prozent. Geben Sie an, für welche Farbkombination dies zutrifft, und begründen Sie Ihre Entscheidung mit Hilfe einer Rechnung.
- 11
Es gilt:

Durch korrektes Ersetzen der Platzhalter sollen richtige Anwendungen der Strahlensätze entstehen. Schreiben Sie die richtigen Gleichungen vollständig auf Ihr Lösungsblatt.
- 12
Folgende Aufgaben sind Anwendungen von binomischen Formeln. Ersetzen Sie die Platzhalter jeweils durch den entsprechenden Term und schreiben Sie die mathematisch richtige Gleichung auf Ihr Lösungsblatt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?