Gegeben sind die Punkte , und , die in der Ebene liegen, sowie die Gerade , .
Bestimmen Sie die Länge der Strecke . Zeigen Sie, dass das Dreieck bei rechtwinklig ist, und begründen Sie damit, dass die Strecke Durchmesser des Umkreises des Dreiecks ist. (4 P)
(zur Kontrolle: )
Bestimmen Sie eine Gleichung von in Koordinatenform und zeigen Sie, dass die Gerade in liegt. (5 P)
(zur Kontrolle:)
Begründen Sie ohne Rechnung, dass g in der -Ebene liegt. (1 P)
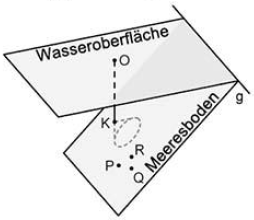
In einem Modell für einen Küstenabschnitt am Meer beschreibt die -Ebene die horizontale Wasseroberfläche und die Gerade die Uferlinie. Die Ebene stellt im betrachteten Abschnitt den Meeresboden dar. Eine Boje schwimmt auf der Wasseroberfläche an der Stelle, die dem Koordinatenursprung entspricht (vgl. Abbildung). Eine Längeneinheit entspricht einem Meter in der Realität.
Bestimmen Sie die Größe des Winkels, unter dem der Meeresboden gegenüber der Wasseroberfläche abfällt. (3 P)
 °
°Ein Fotograf soll für ein Reisemagazin Unterwasserfotos aufnehmen.
Der Fotograf schwimmt entlang der kürzestmöglichen Strecke von der Uferlinie zur Boje. Ermitteln Sie die Länge dieser Strecke. (4 P)
mVon der Boje aus taucht der Fotograf senkrecht bezüglich der Wasseroberfläche nach unten bis zu einer Stelle, deren Abstand zum Meeresboden genau drei Meter beträgt und im Modell durch den Punkt dargestellt wird.
Bestimmen Sie rechnerisch, welche Tiefe unter der Wasseroberfläche der Fotograf bei diesem Tauchvorgang erreicht. (5 P)
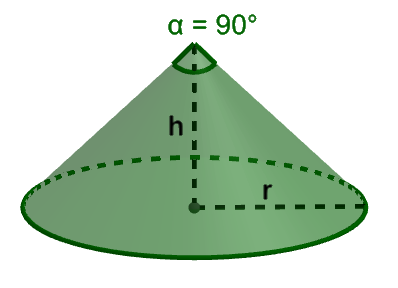
mDrei kleine farbenfrohe Seesterne befinden sich am Meeresboden und werden im Modell durch die Punkte , und dargestellt. Der Fotograf bewegt sich für seine Aufnahmen von der Stelle aus, die im Modell durch den Punkt beschrieben wird, parallel zum Meeresboden. Das Kameraobjektiv zeigt dabei senkrecht zum Meeresboden und hat ein kegelförmiges Sichtfeld mit einem Öffnungswinkel von (vgl. Abbildung).
Beurteilen Sie, ob der Fotograf auf diese Weise eine Stelle erreichen kann, an der er alle drei Seesterne gleichzeitig im Sichtfeld der Kamera sehen kann. (3 P)