Teil 1 Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellungen zum Ausdrucken findest du hier als PDF.

Die Aufgaben im ersten Teil der Abschlussprüfung sind ohne Hilfsmittel (Taschenrechner, Merkhilfe oder Formelsammlung, Tafelwerk) zu lösen.

Versuch es also nur mit Blatt und Stift.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
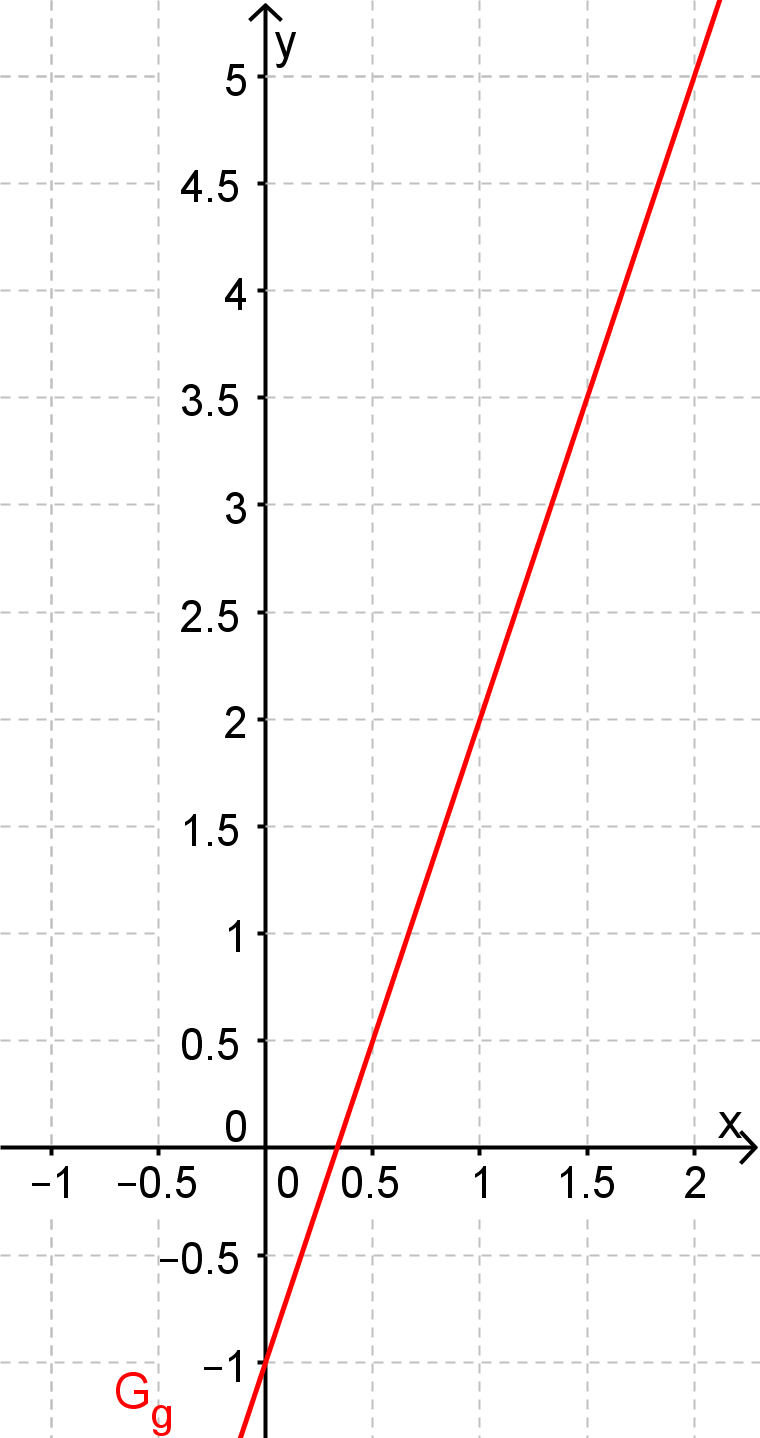
Gegeben ist die lineare Funktoin $g : x \mapsto 3 x - 1$ mit der Definitionsmenge $D_{g} = ℝ$ . Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_{g}$ bezeichnet.
1. Geben Sie die Nullstelle der Funktion g an und erstellen Sie eine Zeichnung vom Graphen $G_{g}$ für $0 \leq x \leq 2$ in einem kartesischen Koordinatensystem.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktion
  Nullstelle
  Die Nullstelle ist bei $x = \frac{1}{3}$ .
  Zeichnung des Graphen
  Verwende z.B. den y-Achsenabschnitt $T (0 | - 1)$ und die Nullstelle $N (\frac{1}{3} | 0)$ und verbinde die beiden Punkte. Achte darauf, dass deine y-Achse groß genug ist ( $- 1 \leq x \leq 5$ ).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Im Idealfall kannst du die Nullstelle im Kopf bestimmen. Falls nicht: Setze den Term mit Null gleich und löse durch Umformen
  Zeichne den Graphen, z.B. mithilfe der Nullstelle und des y-Achsenabschnitts.
2. Berechnen Sie $\int_{0}^{2} g (x) d x$ und interpretieren Sie das Ergebnis geometrisch bezüglich $G_{g}$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimmtes Integral berechnen
  Wert des bestimmten Integrals
  Um den Wert des Integrals zu berechnen, brauchst du eine Stammfunktion von g. Eine mögliche Stammfunktion ist
  $G (x) = 1,5 x^{2} - x$
  Verwende diese bei der Berechnung des Integrals
  $\int_{0}^{2} g (x) d x$ $=$ ${[G (x)]}_{0}^{2}$
  $=$ ${[1,5 x^{2} - x]}_{0}^{2}$
  ↓
  Berechne $G (2) - G (0)$
  $=$ $(1,5 \cdot 2^{2} - 2) - (1,5 \cdot 0^{2} - 0)$
  $=$ $4$
  Geometrische Interpretation
  Integrale werden häufig zur Berechnung von Flächeninhalten verwendet. Da hier allerdings ein Teil der Fläche unterhalb der x-Achse liegt und ein anderer Teil oberhalb, hast du gerade nicht den Flächeninhalt berechnet, sondern die Flächenbilanz.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Wert des bestimmten Integrals. Dazu musst du die Stammfunktion bilden und den Wert der Obergrenze minus den Wert der Untergrenze rechnen
  Beim Interpretieren kannst du dir zum Beispiel überlegen, wie du das Integral im Graph veranschaulichen würdest.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die folgende Abbildung zeigt einen Ausschnitt des Graphen $G_{h}$ einer ganzrationalen Funktion h dritten Grades mit der Definitionsmenge $D_{h} = ℝ$ .
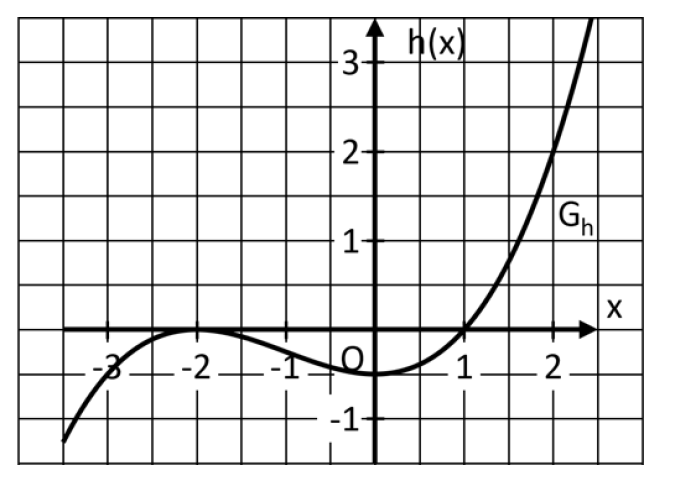
Entscheiden Sie anhand des Graphen $G_{h}$ , ob die nachfolgenden Aussagen jeweils wahr oder falsch sind. Begründen Sie jeweils Ihre Entscheidung.
Die Nullstellen und die Extremstellen von h sind ganzzahlig und können der Abbildung entnommen werden.
1. Es gilt: $h^{'} (x) < 0$ für $x \in] - 2; 1 [$
  
  Du siehst in der Abbildung, dass der Graph von $h$ nur zwischen $- 2 < x < 0$ fällt und danach wieder steigt.
  Folglich ist die Aussage falsch, denn $h^{'} (x) > 0$ für $x \in] 0; 1 [$ .
  Wenn du die Aussage für wahr gehalten hast, hast du vielleicht $h$ und $h^{'}$ verwechselt: die Aussage $h (x) < 0$ für $x \in] - 2; 1 [$ ist nämlich wahr.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Du brauchst Wissen über den Zusammenhang vom Graph einer Funktion und seiner Ableitung:
  Fällt $G_{h}$ in einem Intervall, so verläuft $G_{h^{'}}$ in diesem Intervall unterhalb der x-Achse.
  Umgekehrt verläuft $G_{h^{'}}$ oberhalb der x-Achse, also $h^{'} (x) > 0$ falls $G_{h}$ in diesem Intervall streng monoton steigt.
2. Der Graph der Stammfunktion H von h besitzt einen Terrassenpunkt
  
  Die Aussage ist folglich korrekt. Bei $x = - 2$ hat $G_{h}$ eine doppelte Nullstelle, also hat der Graph von $G_{H}$ dort eine waagerechte Tangente aber eben keine Extremstelle. Es ist also ein Terrassenpunkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für diese Aufgabe musst du den Zusammenhang zwischen dem Graph einer Funktion und seiner Stammfunktion kennen.
  Hat der Graph einer Funktion eine doppelte Nullstelle, so hat seine Stammfunktion dort einen Terrassenpunkt.
3. Es gilt $h (- 2) + h^{'} (0) > 0$
  
  Du kannst direkt aus dem Graphen ablesen, dass $h (- 2) = 0$ .
  Bei $x = 0$ hat der Graph von h eine Extremstelle, deshalb gilt dort $h^{'} (0) = 0$
  Insgesamt ist die Aussage also falsch, denn $h (- 2) + h^{'} (0) = 0 + 0 = 0$ und somit ist der Wert nicht größer als 0.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Funktionswerte von h kannst du der Abbildung direkt entnehmen
  Funktionswerte von h' kannst du über die Tangenten bekommen.
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Eine nach oben geöffnete Parabel besitzt den Scheitelpunkt $S (2 | 2 k - 1)$ mit $k \in ℝ$ . Die zugehörige quadratische Funktion $p_{k} : x \mapsto p_{k} (x)$ ist auf ganz $ℝ$ definiert.
Bestimmen Sie alle Werte für k, sodass die Parabel die x-Achse genau zweimal schneidet.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Die Parabel ist nach oben geöffnet.
Deshalb muss der Scheitelpunkt unterhalb der x-Achse liegen.
Der Scheitelpunkt hat die Koordinaten $S (2 | 2 k - 1)$ , also muss $y_{S} = 2 k - 1$ kleiner als 0 sein.
$2 k - 1$ $<$ $0$ $+ 1$
$2 k$ $<$ $1$ $: 2$
$k$ $<$ $\frac{1}{2}$
Für alle $k < \frac{1}{2}$ schneidet der Graph die x-Achse zweimal.
Beachte die Öffnungsrichtung der Parabel.
Überlege dir anschließend, was für die y-Koordinate des Scheitelpunktes gelten muss, damit die x-Achse zweimal geschnitten wird.
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion f mit der Funktionsgleichung $f (x) = 2 \cdot e^{- x + 1} - 1$ und der Definitionsmenge $D_{f} = [1; \infty [.$
Bestimmen Sie die Wertemenge von f.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Grenzwert für $x \to \infty$
Eine grobe Skizze hilft dir dabei, dir den Graphen besser vorzustellen. Für das Unendlichkeitsverhalten interessiert dich dabei nur die Spiegelung und die Verschiebung in y-Richtung.
Der Graph von $f (x) = 2 \cdot e^{- x + 1} - 1$ hat die Asymptote $y_{A} = - 1$ (Verschiebung um 1 nach unten)
Der Graph ist nicht an der x-Achse gespiegelt, aber an der y-Achse (da $e^{- x}$ ).
Verwende den Schieberegler im Applett, um dir die beiden Veränderungen und ihren Einfluss auf die Wertemenge anzuschauen. Am Ende siehst du den tatsächlichen Graph mit uneingeschränkter Definitionsmenge:
Da der Graph von oben kommend streng monoton fällt, nähert er sich also für $x \to + \infty$ seiner Asymptote an:
$l i m_{x \to + \infty} f (x) = - 1$
Funktionswert am linken Rand
Der linke Rand der Definitionsmenge $D_{f} = [1; + \infty [$ ist eingeschlossen, deshalb gibt es dort ein Randextremum, das direkt in der Wertemenge vorkommt. Setze $x = 1$ in den Term ein:
$f (1) = 2 \cdot e^{- 1 + 1} - 1 = 2 \cdot e^{0} - 1 = 2 - 1 = 1$
Wertemenge angeben
Der Graph nähert sich der Asymptote $y_{A} = - 1$ an und hat als größten Funktionswert im Definitionsbereich $y = 1$ . Daraus ergibt sich die Wertemenge $W =] - 1; 1]$ .
Da der Definitionsbereich $D_{f} = [1; \infty [$ eingeschränkt ist, muss man mehrere Sachen einbeziehen:
Wie ist das Verhalten für $x \to \infty$ , also für große x-Werte? (Globalverlauf)
Welchen Wert nimmt die Funktion bei $x = 1$ an? (Randextrempunkt)
Dabei musst du beachten, dass der Funktionsgraph sowohl gespiegelt als auch verschoben wurde (Die Streckung um den Faktor 2 ist für den Grenzwert nicht relevant).
Der Graph hat außerdem keine weiteren Extrempunkte neben dem Randextremum, da es sich um eine einfache Exponentialfunktion der Form $f (x) = a \cdot b^{c (x + d)} + y_{A}$ handelt.
5
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Lösen Sie die beiden folgenden Gleichungen über der Grundmenge der reellen Zahlen
1. $x^{3} - 2 x^{2} + x = 0$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: binomische Formeln
  $x^{3} - 2 x^{2} + x$ $=$ $0$
  ↓
  Da auf der linken Seite in jedem Summand ein x vorkommt, kannst du ausklammern.
  $x (x^{2} - 2 x + 1)$ $=$ $0$
  Der Satz vom Nullprodukt besagt, dass ein Produkt genau dann 0 wird, wenn mindestens ein Faktor 0 ist. Betrachte also die Faktoren einzeln:
  $x = 0$ oder $x^{2} - 2 x + 1 = 0$
  Der vordere Teil ist bereits fertig. $x = 0$ ist eine Lösung.
  Weiter geht es mit dem hinteren Teil:
  Die Mitternachtsformel funktioniert, aber am einfachsten ist die 2. binomische Formel
  ↓
  $x^{2} - 2 x + 1$ $=$ $0$
  ↓
  2. binomische Formel $a^{2} - 2 a b + b^{2} = (a - b)^{2}$
  ${(x - 1)}^{2}$ $=$ $0$
  Eine weitere Lösung liegt also bei $x - 1 = 0$ , also bei $x = 1$ .
  Die Lösungsmenge ist also $𝕃 = {0; 1}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Prüfe zunächst, ob du ausklammern kannst.
  Da du keine Hilfsmittel zur Verfügung hast, musst du die Lösungsformel für quadratische Gleichungen (Mitternachtsformel) entweder auswendig können oder die binomische Formel erkennen.
2. $(e^{x} - 2)^{2} - 4 = 0$
  
  ${(e^{x} - 2)}^{2} - 4$ $=$ $0$ $+ 4$
  ${(e^{x} - 2)}^{2}$ $=$ $4$
  ↓
  Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt
  $e^{x} - 2$ $=$ $\pm 2$
  Betrachte jede Gleichung einzeln
  Zuerst $e^{x} - 2 = - 2$
  ↓
  $e^{x} - 2$ $=$ $- 2$ $+ 2$
  $e^{x}$ $=$ $0$
  Diese Gleichung hat keine Lösung, denn $e^{x} > 0$ (der Graph verläuft stets über der x-Achse)
  Als nächstes $e^{x} - 2 = 2$
  ↓
  $e^{x} - 2$ $=$ $2$ $+ 2$
  $e^{x}$ $=$ $4$
  ↓
  Löse mithilfe des natürlichen Logarithmus aus.
  $x$ $=$ $\ln 4$
  Es gibt also nur eine Lösung: $x = \ln 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gibt mehrere Wege zum Ziel. Ohne Hilfsmittel ist es jedoch am einfachsten, die Gleichung umzuformen.
  Achtung: Wenn man die Klammer ausmultipliziert, muss man das Substitutionsverfahren verwenden. Diese Lösung zeigt einen alternativen Weg.
6
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist eine Modellfunktion zur Beschreibung der Entwicklung einer Bakterienpopulation im Labor durch $B : t \mapsto 2 \cdot 10^{6} \cdot {(\frac{1}{2})}^{t}$ mit $t \in ℝ_{0}^{+}$ . Dabei steht die Variable t für die seit Beobachtungsbeginn vergangene Zeit in Stunden und $B (t)$ für die Bakterienzahl in einer Petrischale.
Formulieren Sie eine mögliche Problemstellung im Sinne der vorliegenden Thematik, deren Lösung auf die Gleichung $0,4 = {(\frac{1}{2})}^{t_{1}}$ führt, und lösen Sie die Gleichung nach $t_{1}$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: expontentielles Wachstum
Aufbau des Funktionsterms
Der Term hat die Form $B (t) = a \cdot b^{t}$ . Dabei steht $a$ für den Startwert. Zu Beginn der Messung sind also 2 Millionen Bakterien vorhanden.
Der Wachstumsfaktor $b = \frac{1}{2}$ zeigt, dass sich die Bakterienzahl pro Stunde halbiert (denn $t$ beschreibt die Zeit in Stunden.
Da in der Gleichung $0,4 = {(\frac{1}{2})}^{t_{1}}$ der Startwert nicht mehr vorkommt, ist direkt nach dem verbliebenen Prozentsatz gefragt.
Die Gleichung hilft also zu ermitteln, wann nur noch 40% der ursprünglich vorhandenen Bakterien in der Petrischale sind.
Lösen der Gleichung
Die Gleichung wird mithilfe des Logarithmus gelöst:
$0,4$ $=$ ${(\frac{1}{2})}^{t_{1}}$
$t_{1}$ $=$ $\log_{(\frac{1}{2})} (0,4)$
Überlege dir, welche Bedeutungen $2 \cdot 10^{6}$ und $\frac{1}{2}$ im Sachkontext haben.
Schau dir als nächstes an, was in der gefragten Gleichung noch übrig ist und beschreibe die Situation
Zum Auflösen benötigst du den Logarithmus.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\int_{0}^{2} g (x) d x$	$=$	${[G (x)]}_{0}^{2}$
	$=$	${[1,5 x^{2} - x]}_{0}^{2}$
	↓	Berechne $G (2) - G (0)$
	$=$	$(1,5 \cdot 2^{2} - 2) - (1,5 \cdot 0^{2} - 0)$
	$=$	$4$

$x^{3} - 2 x^{2} + x$	$=$	$0$
	↓	Da auf der linken Seite in jedem Summand ein x vorkommt, kannst du ausklammern.
$x (x^{2} - 2 x + 1)$	$=$	$0$

Die Mitternachtsformel funktioniert, aber am einfachsten ist die 2. binomische Formel
	↓
$x^{2} - 2 x + 1$	$=$	$0$
	↓	2. binomische Formel $a^{2} - 2 a b + b^{2} = (a - b)^{2}$
${(x - 1)}^{2}$	$=$	$0$

${(e^{x} - 2)}^{2} - 4$	$=$	$0$	$+ 4$
${(e^{x} - 2)}^{2}$	$=$	$4$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt
$e^{x} - 2$	$=$	$\pm 2$

Zuerst $e^{x} - 2 = - 2$
	↓
$e^{x} - 2$	$=$	$- 2$	$+ 2$
$e^{x}$	$=$	$0$

Als nächstes $e^{x} - 2 = 2$
	↓
$e^{x} - 2$	$=$	$2$	$+ 2$
$e^{x}$	$=$	$4$
	↓	Löse mithilfe des natürlichen Logarithmus aus.
$x$	$=$	$\ln 4$

$0,4$	$=$	${(\frac{1}{2})}^{t_{1}}$
$t_{1}$	$=$	$\log_{(\frac{1}{2})} (0,4)$

$2 k - 1$	$<$	$0$	$+ 1$
$2 k$	$<$	$1$	$: 2$
$k$	$<$	$\frac{1}{2}$

Teil 1 Analysis

Nullstelle

Zeichnung des Graphen

Hast du eine Frage oder Feedback?

Wert des bestimmten Integrals

Geometrische Interpretation

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Grenzwert für x→∞

Funktionswert am linken Rand

Wertemenge angeben

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufbau des Funktionsterms

Lösen der Gleichung

Grenzwert für $x \to \infty$