Heft 1
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen vom Prüfungsteil 1 des Mathe MSA 2022.
Ein Taschenrechner ist in diesem Prüfungsteil nicht erlaubt.
- 1
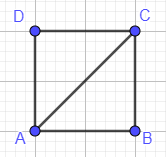
Gegeben ist das folgende Quadermodell. Welche Kante steht senkrecht auf der Kante ? Kreuze an. (1 Punkt)
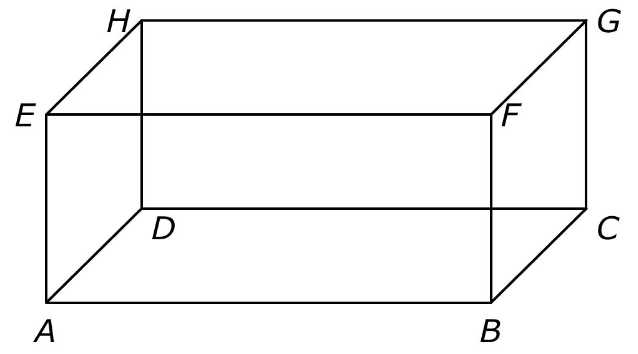
- 2
Vervollständige die Tabelle für die antiproportionale Zuordnung. (1 Punkt)
- 3
Bei einem Glücksspiel soll die Wahrscheinlichkeit für einen Gewinn betragen. Beschreibe ein Glücksspiel, auf das dies zutrifft. (1 Punkt)
- 4
Sieben Freunde haben ihr Taschengeld miteinander verglichen.
Angaben in Euro pro Woche: .
Gib die folgenden Mittelwerte an:
(2 Punkte)
- 5
Für die Strecke, die ein Körper im freien Fall bei Vernachlässigung des Luftwiderstands zurücklegt, gilt folgende Regel:
Quadriere die Fallzeit (in ) und multipliziere das Ergebnis mit 5, so erhältst du die Fallstrecke (in ).
Gabor hat nach dieser Regel mithilfe einer Tabellenkalkulation zu unterschiedlichen Fallzeiten die zugehörigen Fallstrecken berechnet.

Ergänze die fehlenden Werte in den Zellen D2 und E2. (2 Punkte)
Kreuze die Formel an, mit der der Wert in Zelle C2 berechnet werden kann. (1 Punkt)
- 6
Julia hat die letzte Ziffer ihrer PIN für ihr Handy vergessen. Die Wahrscheinlichkeit, dass sie zweimal falsch rät, beträgt: (1 Punkt)
- 7
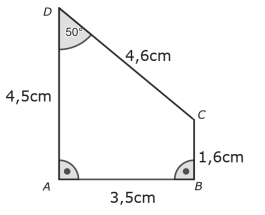
Ergänze zu einem Trapez mit dem Winkel und . (1 Punkt)
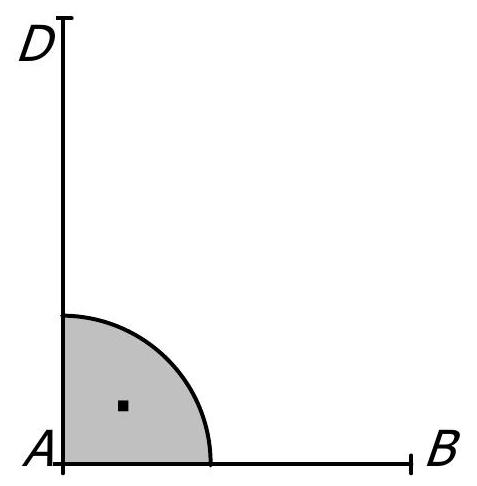
- 8
Entscheide jeweils, ob die Aussage wahr oder falsch ist. Ordne zu. (4 Punkte)
- 9
Gegeben ist die folgende quadratische Funktion in Normalform.
Welche der folgenden Funktionsgleichungen stellt dieselbe quadratische Funktion in der Scheitelpunktform dar? Kreuze an. (1 Punkt)
- 10
Ein großer Platz erhält ein neues Pflaster. sind bereits fertig. Stündlich werden zusätzlich gepflastert.
Entscheide, welche der Funktionsgleichungen die Situation richtig beschreibt. (1 Punkt)
Begründe deine Entscheidung. (1 Punkt)
- 11
Ein Dreieck hat eine Grundseite von und einen Flächeninhalt von .
Gib die Höhe an. (1 Punkt)
- 12
Ein Würfel hat die Kantenlänge . Er wird in zwei gleichgroße Quader zerschnitten.
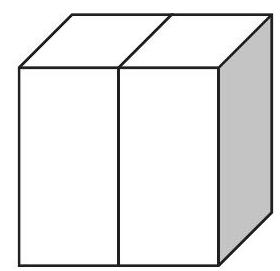
Gib die Seitenlängen , und eines Quaders an.
Gib das Volumen eines Quaders an.
Angenommen, der Würfel wird in 64 gleichgroße Quader zerteilt. Welches Volumen hat dann einer dieser Quader? (3 Punkte)
- 13
Bei einem Test ist das Verhältnis von richtigen zu falschen Antworten 4:3. Der Anteil falscher Antworten beträgt: (1 Punkt)
- 14
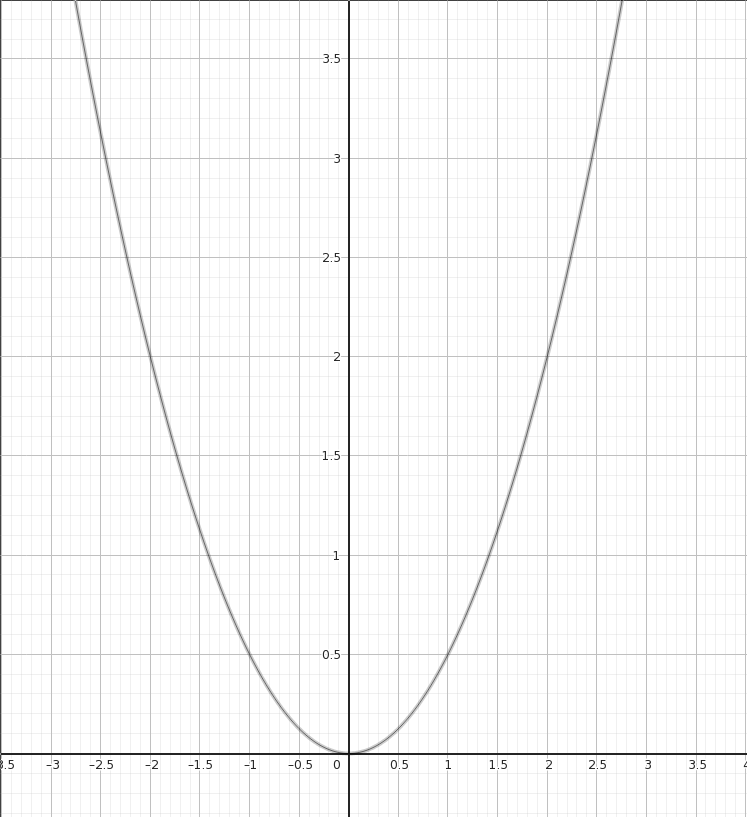
Im Schaubild ist eine Parabel abgebildet. Ihre Funktionsgleichung lautet .
Beschrifte beide Achsen so, dass sie zur abgebildeten Parabel passen. (1 Punkt)
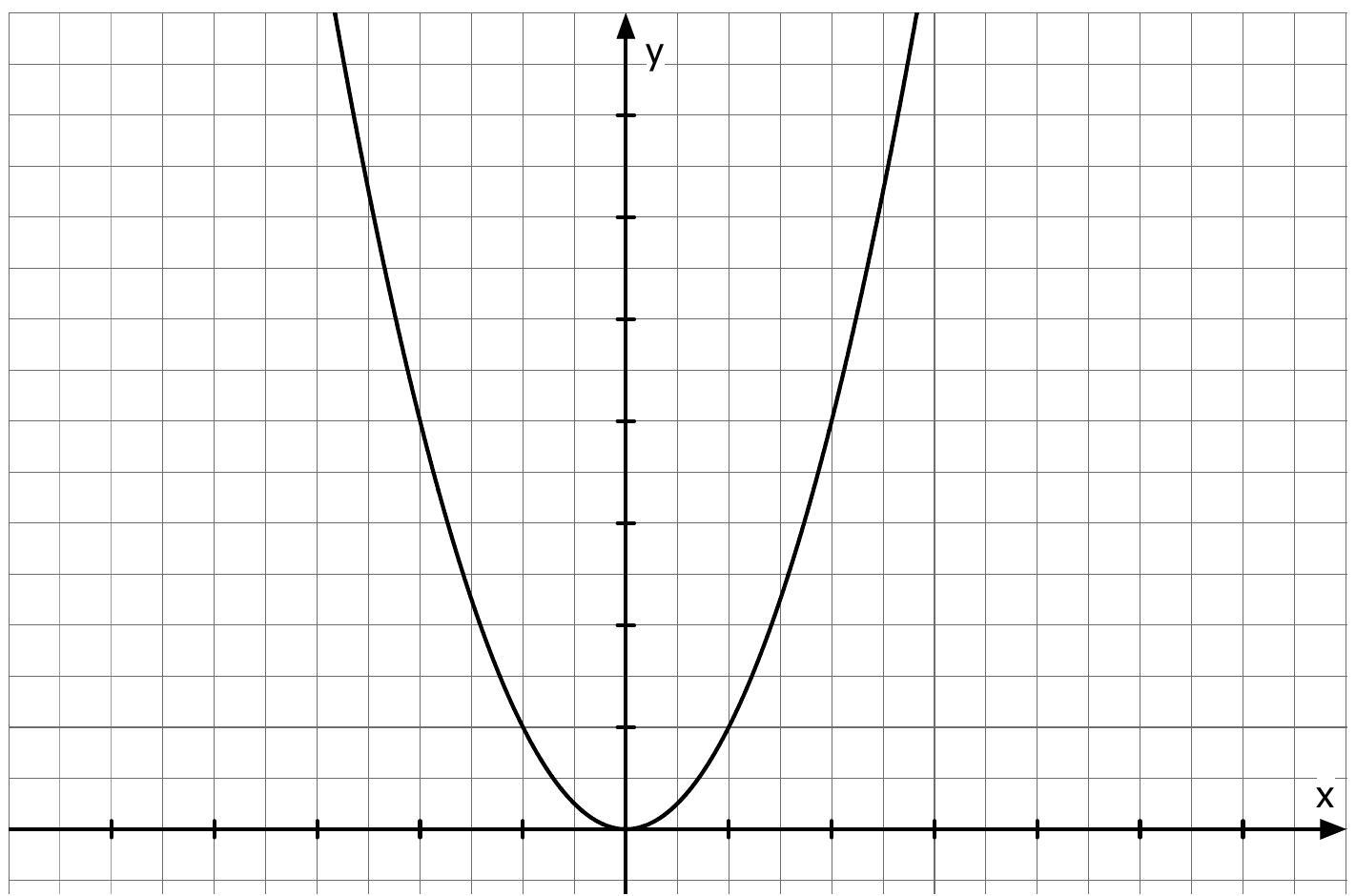
- 15
Ali sagt: „Bildet man aus allen fünf Ziffern und eine beliebige fünfstellige Zahl, so ist diese immer durch 3 teilbar."
Begründe, dass dies stimmt. (1 Punkt)
- 16
Josy sagt: „Wenn zwei Zahlen durch 5 teilbar sind, dann ist auch ihre Summe immer durch 5 teilbar."
Begründe, dass dies stimmt. (1 Punkt)
- 17
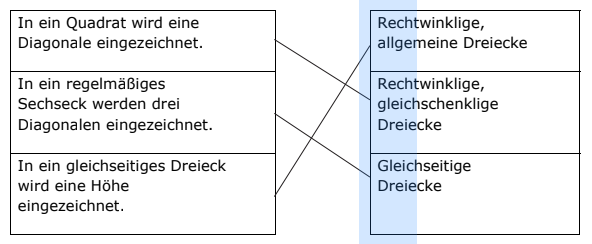
Welche Dreiecke entstehen? Verbinde. (2 Punkte)
Du kannst mit der Maus die Antworten in die Felder ziehen.
- 18
Es wird mit zwei normalen sechsseitigen Spielwürfeln gewürfelt.
Die Wahrscheinlichkeit, dass ein Würfel eine 3 und ein Würfel eine 4 zeigt, beträgt: (1 Punkt)
Die Wahrscheinlichkeit, zwei gleiche Zahlen zu würfeln, beträgt: (1 Punkt)
- 19
Gegeben ist die Gleichung .
Überprüfe durch eine geeignete Rechnung, ob das Zahlenpaar Lösung der Gleichung ist. (1 Punkt)
- 20
Gleiche Buchstaben bezeichnen gleich große Winkel. Wie groß ist der Winkel ? (1 Punkt)
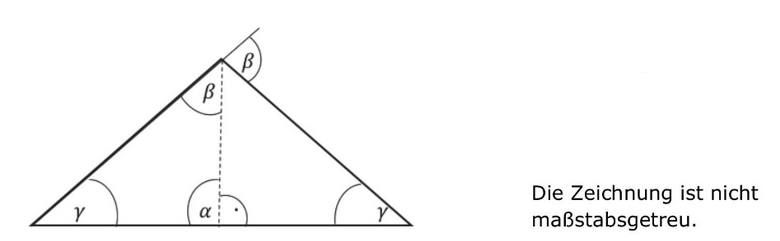
- 21
Ilka fährt mit dem Fahrrad von Itzehoe nach Hohenwestedt. Sie benötigt für die lange Strecke insgesamt eine Fahrtzeit von 80 Minuten. Nach 45 Minuten macht sie eine Pause. Wie viele Kilometer ist sie bis dann etwa gefahren? (1 Punkt)
km
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?