2023

1
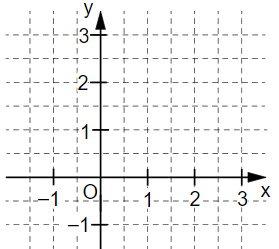
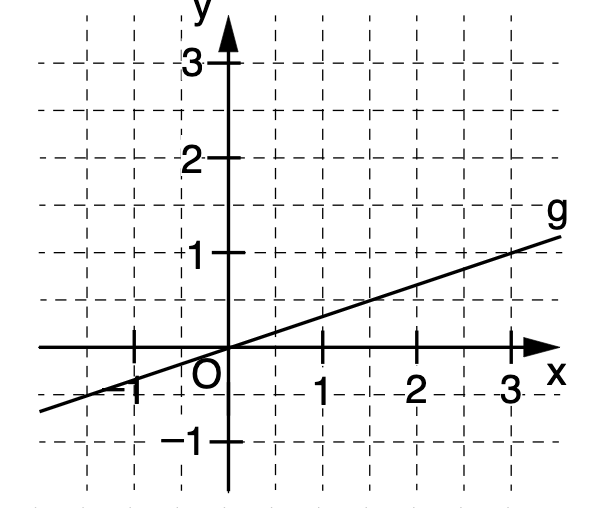
1. Zeichne die Ursprungsgerade $g$ mit der Gleichung $y = \frac{1}{3} \cdot x$ in das Koordinatensystem.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
  Einzeichnen der Geraden $g$ mit der Gleichung $y = \frac{1}{3} x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zeichne eine Gerade, mit der Steigung $\frac{1}{3},$ durch den Ursprung.
2. Überprüfe durch Rechnung, ob der Punkt $P (4 | – 1)$ auf der Gerade $h : y = – 0,25 \cdot x$ liegt.
  
  Überprüfen , ob der Punkt $P (4 | – 1)$ auf der Gerade $h : y = – 0,25 \cdot x$ liegt.
  Einsetzen der Koordinaten des Punktes $P .$
  $- 1 = - 0,25 \cdot 4$
  $- 1 = - 1$
  Der Punkt $P (4 | – 1)$ liegt also auf der Gerade $h : y = – 0,25 \cdot x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze für $x = 4$ und für $y = - 1$ in die Geradengleichung $y = - 0,25 \cdot x$ ein.
2
Der Faktor $3 a c^{2}$ wurde ausgeklammert.
Vervollständige. $6 a c^{3} – 27 a^{2} c^{2} = 3 a c^{2}$ ∙( _________________ )

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ausklammern
Vervollständigen der Klammer.
$6 a c^{3} : 3 a c^{2} = 2 c$
$- 27 a^{2} c^{2} : 3 a c^{2} = - 9 a$
$6 a c^{3} – 27 a^{2} c^{2} = 3 a c^{2} \cdot (2 c - 9 a)$
Teile $6 a c^{3}$ und $- 27 a^{2} c^{2}$ durch $3 a c^{2}$ und schreibe die Werte in die Klammer.
3
Nur eine der folgenden Aussagen ist für jede beliebige Belegung von $x$ wahr. Kreuze diese an.
$x + x = x^{2}$
$3 x - x = 3$
$x^{2} \cdot x^{3} = x^{5}$
$2 x \cdot 3 x = 6 x$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungen allgemein
Überprüfen, welche der Aussagen für jede beliebige Belegung von $x$ wahr ist.
$x + x = x^{2}$ falsch, da $x + x = 2 x$
$3 x - x = 3$ falsch, da $3 x - x = 2 x$
$x^{2} \cdot x^{3} = x^{5}$ richtig!
$2 x \cdot 3 x = 6 x$ falsch, da $2 x \cdot 3 x = 6 x^{2}$
Kreuze entsprechend an.
4
Gib die Lösungsmenge $L$ der folgenden Gleichung an. $2 \cdot (3 x + x^{2}) – 2 x^{2} = x + 10$
$L =$ {______}

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungen
Lösen der Gleichung: $2 \cdot (3 x + x^{2}) – 2 x^{2} = x + 10$
$2 \cdot (3 x + x^{2}) - 2 x^{2}$ $=$ $x + 10$
↓
auflösen der Klammer
$6 x + 2 x^{2} - 2 x^{2}$ $=$ $x + 10$
↓
linke Seite zusammenfassen
$6 x$ $=$ $x + 10$ $- x$
↓
subtrahieren
$5 x$ $=$ $10$ $: 5$
↓
dividieren
$x$ $=$ $2$
$𝕃 = {2}$
Löse die Gleichung, indem Du $x$ berechnest.
5
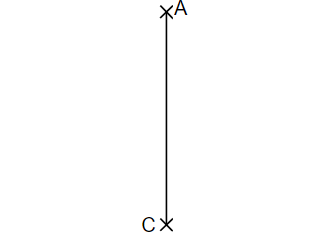
Für das Drachenviereck $A B C D$ gilt: $α = 80 °$ und $γ = 50 °$ . Vervollständige die Zeichnung zum Drachenviereck $A B C D$ mit der Symmetrieachse $A C$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Drachenviereck
Vervollständigen der Zeichnung zum Drachenviereck $A B C D$ mit der Symmetrieachse $A C$ .
Trage den Winkel $α$ am Punkt $𝐀$ an und den Winkel $γ$ am Punkt $𝐂$ an. Beachte die Symmetrieachse.
6
Löse die Klammer auf und fasse so weit wie möglich zusammen.
$(x + 3)^{2} + 4 x =$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Klammern ausmultiplizieren
Auflösen der Klammer und zusammenfassen:
$(x + 3)^{2} + 4 x =$ $=$ $(x + 3) \cdot (x + 3) + 4 x$
↓
ausmultiplizieren der Klammer
$=$ $x^{2} + 6 x + 9 + 4 x$
↓
zusammenfassen
$=$ $x^{2} + 10 x + 9$
Die Lösung lautet: $x^{2} + 10 x + 9$
Multipliziere die Klammer aus und fasse dann zusammen.
7
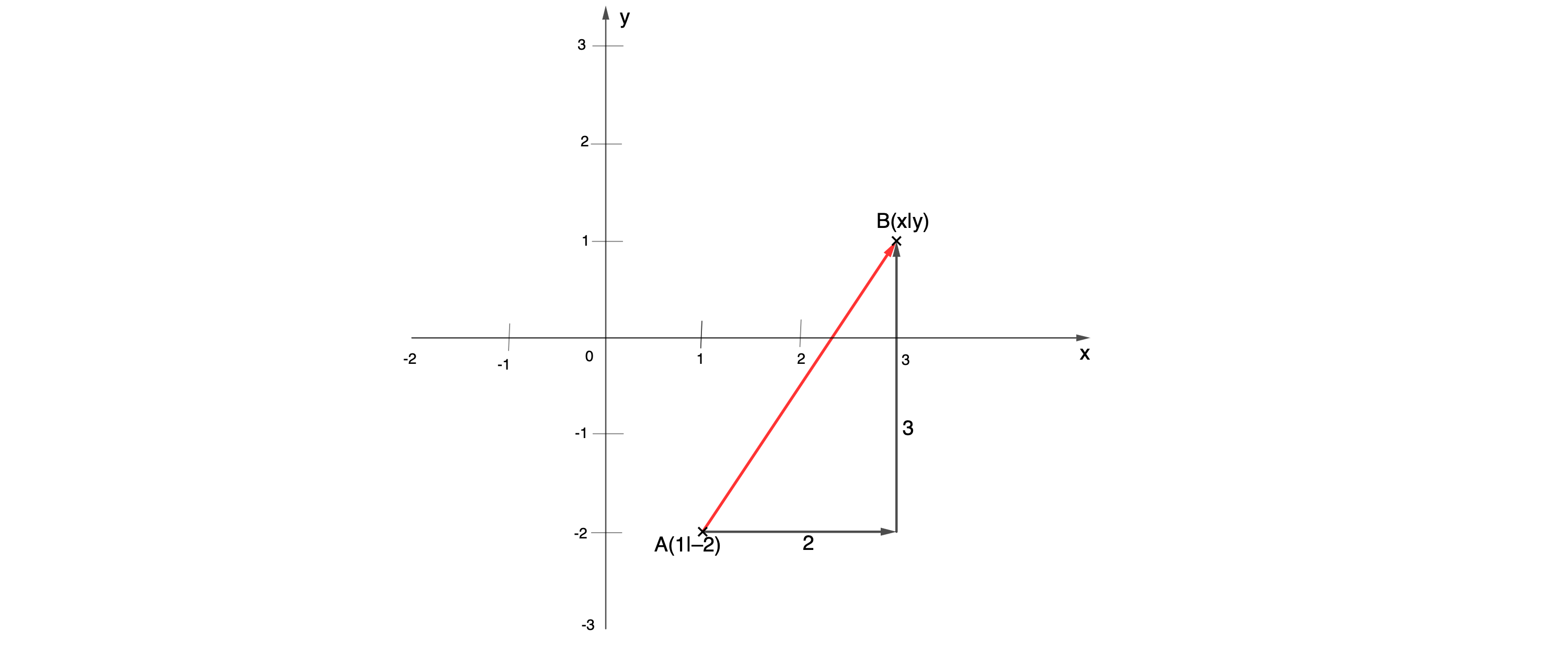
Gegeben sind der Punkt $A (1 | – 2)$ und der Pfeil $\vec{A B} = (\begin{array}{c} 2 \\ 3 \end{array})$ . Gib die Koordinaten $x$ und y des Punktes $B (x | y)$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Berechnen der Koordinaten des Punktes $B (x | y)$
$\vec{A B} = (\begin{array}{c} B_{x} - A_{x} \\ B_{y} - A_{y} \end{array})$
$(\begin{array}{c} 2 \\ 3 \end{array}) = (\begin{array}{c} x - 1 \\ y - (- 2) \end{array})$
$\begin{array}{l} 2 = x - 1 \\ 3 = y + 2 \end{array}$
$\begin{array}{l} - x = - 3 \\ x = 3 \end{array}$
$\begin{array}{l} - y = - 1 \\ y = 1 \end{array}$
Der Punkt $B$ hat die Koordinaten $B (3 | 1)$ , also $(x = 3)$ und $(y = 1)$ .
8
Gegeben ist der quadratische Term $T (x) = 4 \cdot (x – 3)^{2} – 1$ . Eine der folgenden Angaben beschreibt den Extremwert, dessen Art und die dazugehörige Belegung von $x$ für diesen Term korrekt. Kreuze diese an.
$T_{\max} = 3$ für $x = - 1$
$T_{\max} = 4$ für $x = 3$
$T_{\max} = - 3$ für $x = 4$
$T_{\min} = 3$ für $x = - 1$
$T_{\min} = - 1$ für $x = 3$
$T_{\min} = - 1$ für $x = - 3$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Allgemeine Form und Scheitelform einer quadratischen Funktion
Die Scheitelform einer quadratischen Funktion lautet:
$f (x) = a (x - d)^{2} + e$
$d = 3 \Rightarrow x = 3$
$e = - 1 \Rightarrow y = - 1$
Da es sich um eine nach oben geöffnete Parabel handelt, ist der Extremwert ein Minimum, also ist:
$T_{m i n} = - 1$ für $x = 3$
Kreuze entsprechend an.
Der Term $T (x)$ ist in der Scheitelform dargestellt. Beachte, der Term $T (x)$
beschreibt eine nach oben geöffnete Parabel.
9
Pia wünscht sich ein Freigehege für ihre Hühner. Ihr Vater zeigt ihr einen Plan (siehe Skizze), bei dem zwei Wände für zwei Seiten des rechteckigen Geheges genutzt werden sollen. Für die restlichen zwei Seiten sollen insgesamt $15 m$ Zaun vollständig verbaut werden. Gib den Flächeninhalt $A$ des Freigeheges an, wenn es doppelt so lang wie breit sein soll.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Umfang von Rechteck und Quadrat
Die Formel zur Berechnung des Umfangs eines Rechtecks lautet:
$U = 2 \cdot (l + b) \Rightarrow \frac{U}{2} = l + b$
laut Aufgabenstellung gilt: $l = 2 b$ ; $\frac{U}{2} = 15 m$
Berechnen der Breite $b$ des Freigeheges:
$\frac{U}{2} = 2 b + b$
$15$ $=$ $2 b + b$
↓
zusammenfassen
$15$ $=$ $3b$ $: 3$
↓
dividieren und Seiten tauschen
$b$ $=$ $5$
Die Breite des Rechtecks beträgt also $b = 5 m$ ; die Länge $l$ ist dann $5 \cdot 2 = 10 m .$
Berechnen des Flächeninhalts $A$ des Rechtecks:
$A = l \cdot b \Rightarrow A = 10 \cdot 5 = 50 m^{2}$
Der Flächeninhalt des Freigeheges beträgt: $50 m^{2}$
Das Freigehege hat die Form eines Rechtecks, wobei $2$ Seiten des Rechtecks durch eine Wand begrenzt sind. Die Länge des Zaunes $(15 m)$ entspricht also dem halben Umfang dieses Rechtecks. Berechne die Länge und die Breite des Rechtecks.
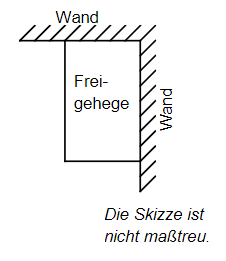
10
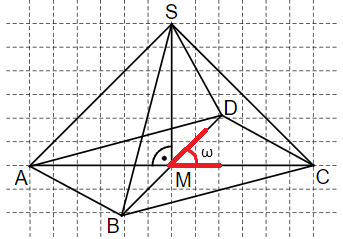
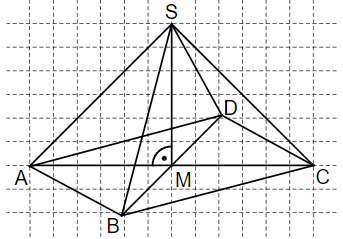
Die Pyramide $A B C D S$ hat eine quadratische Grundfläche $A B C D$ mit $| A C | = 6 cm$ und die Höhe $| M S | = 3 cm$ . Paul sollte ein Schrägbild dieser Pyramide nach folgenden Vorgaben zeichnen: Schrägbildachse $A C$ ; $q = 0,5$ ; $ω = 60 °$ . Die Abbildung zeigt sein Ergebnis. Eine der Vorgaben hat er dabei nicht korrekt umgesetzt. Beschreibe den Fehler, den er bei der Zeichnung gemacht hat.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
Paul hat für seine Zeichnung den Verzerrungswinkel $ω$ mit einem falschen Maß verwendet.
Beachte den Verzerrungswinkel $ω$ .
11
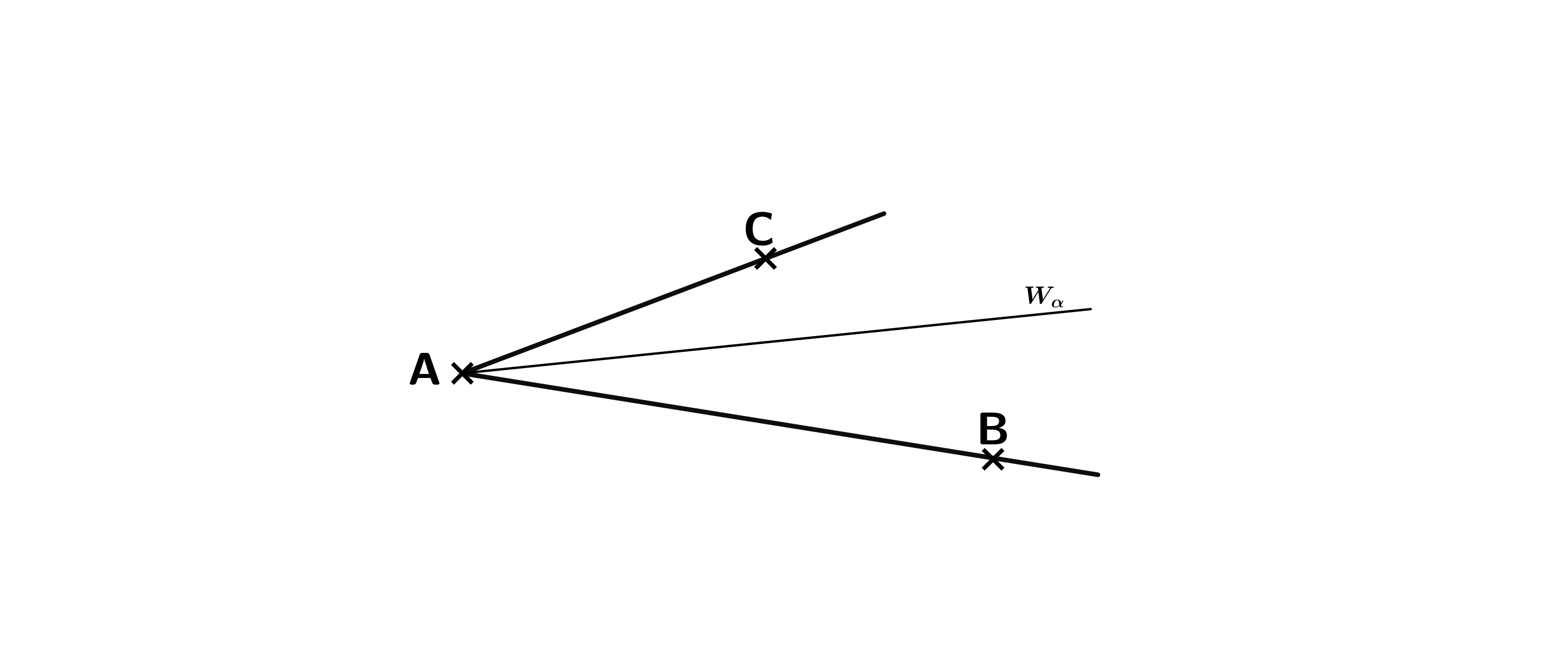
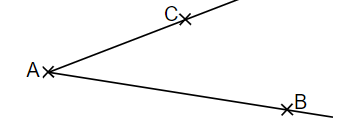
Kennzeichne die Menge aller Punkte, die von den Halbgeraden $[A B$ und $[A C$ den gleichen Abstand haben.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkelhalbierende
Zeichnen der Winkelhalbierenden $W_{α}$
Alle Punkte, die von den Halbgeraden $[A B$ und $[A C$ den gleichen Abstand haben liegen auf der Winkelhalbierenden $W_{α}$ .
Konstruiere die Winkelhalbierende des $∠ C A B$
12
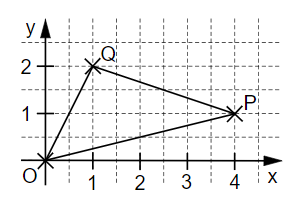
Der Flächeninhalt $A$ des Dreiecks $O P Q$ soll mit Hilfe einer Determinante ermittelt werden. Einer der folgenden Lösungsansätze ist richtig.
$A = \frac{1}{2} \cdot | \begin{array}{cc} 4 & 1 \\ 1 & 2 \end{array} | F E$
$A = \frac{1}{2} \cdot | \begin{array}{cc} 1 & 4 \\ 2 & 1 \end{array} | F E$
$A = \frac{1}{2} \cdot | \begin{array}{cc} 1 & 2 \\ 2 & 1 \end{array} | F E$
$A = \frac{1}{2} \cdot | \begin{array}{cc} - 1 & 4 \\ - 2 & 1 \end{array} | F E$
$A_{Δ} = \frac{1}{2} \cdot | \begin{array}{cc} v_{1} & w_{1} \\ v_{2} & w_{2} \end{array} | F E = \frac{1}{2} \cdot (v_{1} \cdot w_{2} - v_{2} \cdot w_{1}) F E$
$\vec{O P} = \vec{v}$ mit $\vec{v} = (\begin{array}{c} 4 \\ 1 \end{array}) - (\begin{array}{c} 0 \\ 0 \end{array}) = (\begin{array}{c} 4 \\ 1 \end{array})$
$\vec{O Q} = \vec{w}$ mit $\vec{w} = (\begin{array}{c} 1 \\ 2 \end{array}) - (\begin{array}{c} 0 \\ 0 \end{array}) = (\begin{array}{c} 1 \\ 2 \end{array})$
$A_{Δ} = \frac{1}{2} | \begin{array}{cc} 4 & 1 \\ 1 & 2 \end{array} | F E$
Bestimme zunächst die Vektoren $\vec{O P}$ und $\vec{O Q}$ .
Setze die Einträge der Vektoren in die Formel für den Flächeninhalt ein.
$A_{Δ} = \frac{1}{2} \cdot | \begin{array}{cc} v_{1} & w_{1} \\ v_{2} & w_{2} \end{array} | F E$
13
Ergänze den Nenner, so dass der Bruchterm $T (x)$ die Definitionsmenge D $= ℚ$ \{ $3$ } hat.
$T (x) = \frac{5}{□}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen lösen
$T (x) = \frac{5}{x - 3}$
Wähle den Nenner so, dass dieser $0$ wird, für $x = 3.$
14
Gib die Lösungsmenge L der Bruchgleichung $\frac{1}{2} = \frac{6}{x - 2}$ mit D= $ℚ$ \ { $2$ }.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchgleichungen lösen
$\frac{1}{2}$ $=$ $\frac{6}{x - 2}$ $(x - 2)$
↓
multipliziere
$\frac{x - 2}{2}$ $=$ $6$ $\cdot 2$
↓
multipliziere
$x - 2$ $=$ $12$ $+ 2$
↓
addiere
$x$ $=$ $14$
L={14}
Multipliziere die Gleichung mit dem Nenner (x−2).
Löse dann die lineare Gleichung.
15
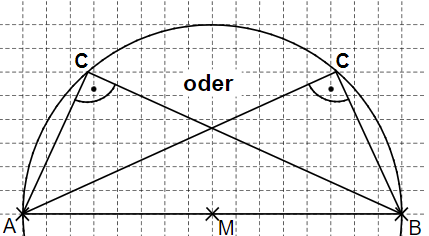
Thomas möchte mithilfe des Thaleskreises ein bei $C$ rechtwinkliges Dreieck $A B C$ zeichnen. Vervollständige seine Zeichnung zum Dreieck $A B C$ mit dem Flächeninhalt $A$ von $12 {cm}^{2}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Thales
Dreiecksfläche: $A_{Δ} = \frac{1}{2} \cdot Länge von g \cdot Höhe h$
$\Rightarrow$ $h = \frac{A_{Δ}}{g} \cdot 2$
Gegeben: $A_{Δ} = 12 {cm}^{2}$
Gegeben: $g = A B = 8 cm$
$\Rightarrow$ $h = \frac{12 {cm}^{2}}{8 cm} \cdot 2 = 3 cm$
Wähle auf dem Thaleskreis über $[A B]$ einen Punkt $C$ , der von $[A B]$ den Abstand $3 cm$ hat.
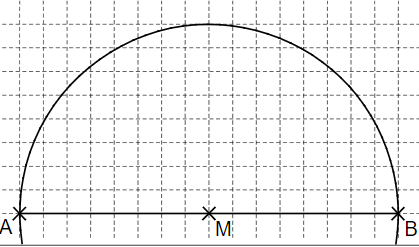
16
$6$ Würfel mit einem Volumen von je $8 {cm}^{3}$ werden wie abgebildet in einen Karton gepackt (s. Skizze). Sie füllen die Breite und die Länge des Kartons vollständig aus. Nur oben bleibt ein Hohlraum mit einer Höhe von $1 cm$ . Gib an, welches Volumen $V$ der Karton hat.
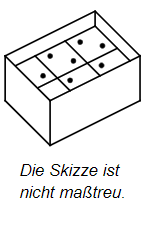
Das Volumen des Kartons beträgt ${cm}^{3}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Würfel (Kubus)
Gesamtvolumen der Würfel:
$6 \cdot 8 {cm}^{3} = 48 {cm}^{3}$
Volumen eines Würfels: $V_{Würfel} = a^{3}$
$\Rightarrow$ Die Seitenlänge eines Würfels beträgt $2 cm .$
Die Grundfläche des Hohlraums hat eine Länge von
$3 \cdot 2 cm = 6 cm$ (3 Würfel nebeneinander) und eine Breite von
$2 \cdot 2 cm = 4 cm$ (2 Würfel nebeneinander).
Höhe des Hohlraums : $1 cm$ (siehe Angabe)
Volumen des Hohlraums:
$6 cm \cdot 4 cm \cdot 1 cm = 24 {cm}^{3}$
$V_{Karton } = 48 {cm}^{3} + 24 {cm}^{3} = 72 {cm}^{3}$

Das Volumen $V$ des Kartons beträgt $72 {cm}^{3}$ .

Berechne das Gesamtvolumen der Würfel und das Volumen des Hohlraums.
Addiere diese beiden Volumina für das Volumen des Kartons.
17
Christian hat $160$ € gespart und geht mit diesem Geld einkaufen. Er findet eine Jeans und ein Hemd. Die Jeans ist doppelt so teuer wie das Hemd. Nachdem Christian bezahlt hat, verbleiben ihm noch $25$ % seines Ersparten. Gib an, wie teuer die Jeans war.
Die Jeans kostete _________€.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
Ersparnisse: 160€
$160 \hat{=} 100$ %
$1,60 \hat{=} 1$ %
$40 \hat{=} 25$ %
$160 € - 40 € = 120 €$
Christian hat also $120 €$ ausgegeben.
Preis für ein Hemd: $x$
Preis für eine Jeans: $2 x$
$x + 2 x = 120$
$x = 40$
Die Jeans hat also $80 €$ gekostet.
Berechne zuerst wieviel Christian ausgibt.
18
Eine Autobahnbrücke mit sechs Pfeilern (siehe maßstabsgetreue Abbildung) wird saniert.
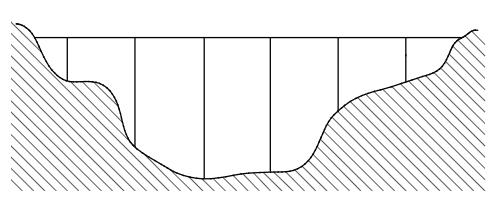
Am ersten Tag wurden $120 m$ der Fahrbahn erneuert, das sind $20$ % der gesamten Brückenlänge. Anschließend werden die Brückenpfeiler instandgesetzt. Welche Höhe hat der längste Brückenpfeiler? Gib deinen Lösungsweg an.
Der längste Brückenpfeiler ist _________ $m$ hoch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
$120 m \hat{=} 20$ %
$600 m \hat{=} 100$ %
$\Rightarrow$ Die Länge der Brücke beträgt $600 m$ .
Miss nun die Länge der Brücke und die Länge des höchsten Pfeilers in der Zeichnung.
Länge Brücke: $9 cm$
Länge des höchsten Pfeilers: $3 cm$
$\Rightarrow$ Die Brücke ist $3$ mal so lang, wie der höchste Pfeiler. $600 m : 3 = 200 m$ .
Der längste Brückenpfeiler ist $200 m$ hoch.
19
Im abgebildeten Diagramm sind jeweils die Mitgliederzahl und die Anzahl der gewonnenen Meisterschaften von fünf Handballvereinen dargestellt.
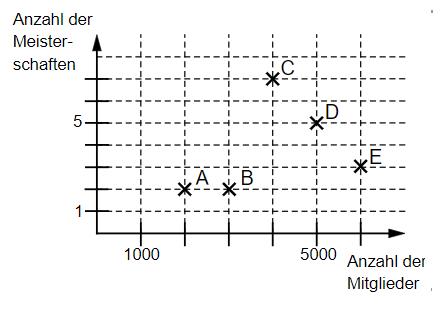
Eine Aussage zum Diagramm ist falsch. Kreuze diese an.
Verein D hat mehr als doppelt so viele Mitglieder wie Verein A.
Die Vereine C und D haben jeweils mehr als ein Viertel aller Meisterschaften gewonnen.
Verein B hat um $50$ % mehr Mitglieder als Verein A.
Verein D hat halb so viele Meisterschaften gewonnen wie die Vereine B und C zusammen.
Aus dem Diagramm kannst du folgendes ablesen.
Verein A hat $2000$ Mitglieder und Verein $D$ hat $5000$ Mitglieder, also mehr als doppelt so viele wie Verein A.
Alle Vereine zusammen haben
$2 + 2 + 7 + 5 + 3 = 19$ Meisterschaften gewonnen.
$19 : 4 = 4,75$
Verein $C$ hat $7$ Meisterschaften und Verein $D$ hat $5$ Meisterschaften gewonnen. Sie haben also beide mehr als ein Viertel der Meisterschaften gewonnen.
Verein $B$ hat $3000$ Mitglieder, Verein $A$ hat $2000$ Mitglieder.
$2000 \hat{=} 100$ %
$1000 \hat{=} 50$ %
$\Rightarrow$ Verein $B$ hat $50$ % mehr Mitglieder als Verein $A .$
Die Vereine $B$ und $C$ haben zusammen $2 + 7 = 9$ Meisterschaften, der Verein $D$ hat $5$ Meisterschaften gewonnen.
$\Rightarrow$ Verein D hat mehr als halb so viele Meisterschaften gewonnen wie die Vereine $B$ und $C$ zusammen.
20
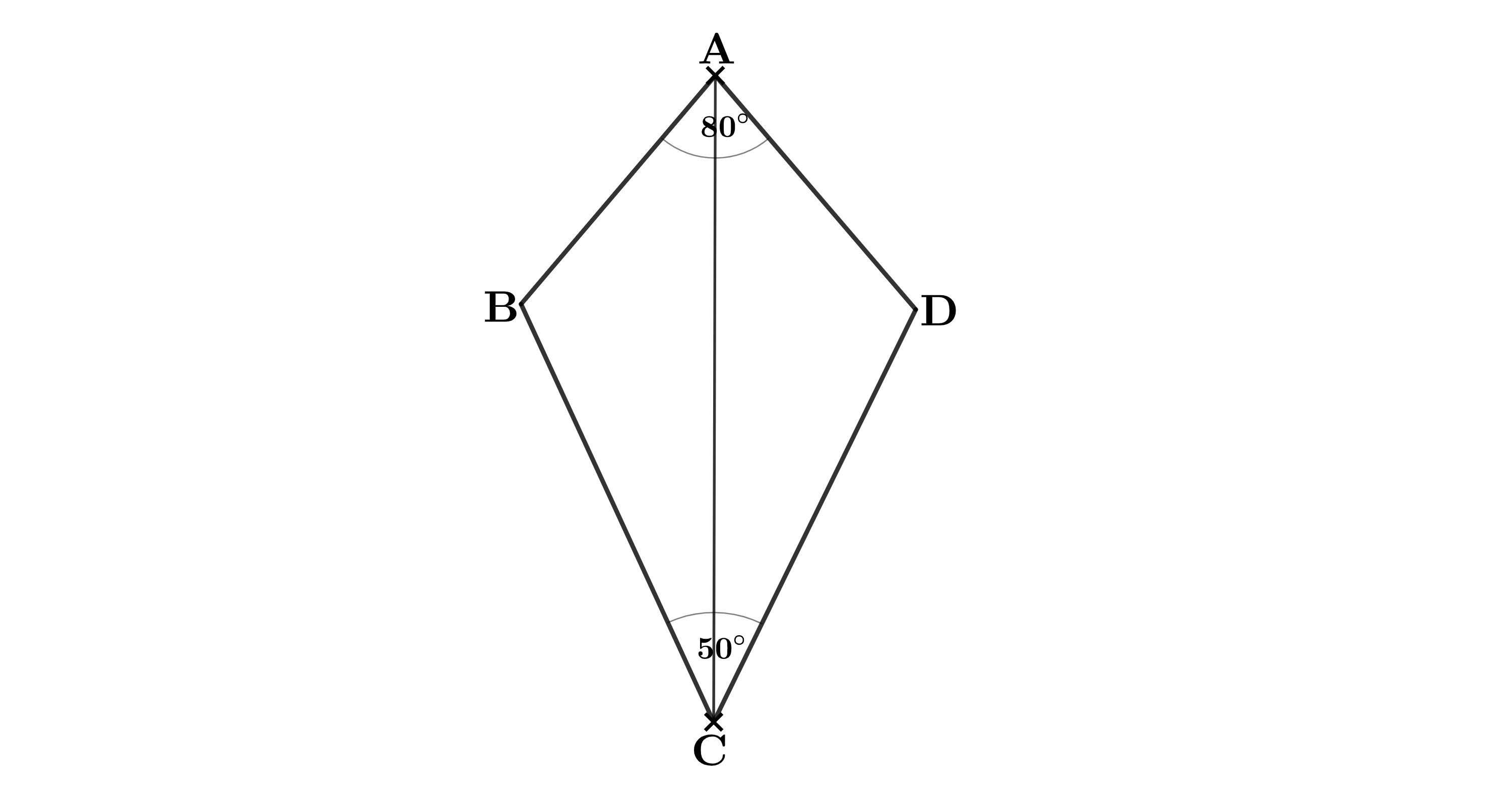
Gib die Winkelmaße $α$ und $β$ an.
Es gilt: $| A M | = | M C |$ und $g | | h$ .
$α =$ ____°; $β =$ ____°.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Winkel linkes Dreieck: $180 ° - (180 ° - 50 °) - 30 ° = 20 °$
$\Rightarrow$ $α = 180 ° - 20 ° = 160 °$
Dreieck $A C B$ ist gleichschenklig. $\Rightarrow$ Winkel $∢ A C B = 50 °$
$∢ C B M = 180 ° - 50 ° - 90 ° = 40 °$
$\Rightarrow$ $β = 90 ° - 40 ° = 50 °$
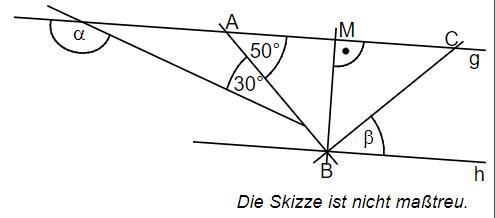
21
Max hat mehrmals eine Münze geworfen und die Ergebnisse in einer Tabelle festgehalten.
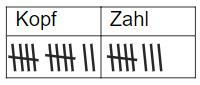
Gib die relative Häufigkeit des Ergebnisses „Kopf“ an.
Die relative Häufigkeit des Ergebnisses „Kopf“ beträgt

Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
$relative Häufigkeit = \frac{absolute Häufigkeit}{Anzahl der Versuche}$
Anzahl Versuche: $20$
absolute Häufigkeit "Kopf": $12$
relative Häufigkeit "Kopf"= $\frac{12}{20}$
Die relative Häufigkeit des Ergebnisse "Kopf" berträgt $\frac{12}{20}$ .
Zähle die Anzahl, wie oft Kopf und Zahl geworfen wurde.
Bilde jeweils die relative Häufigkeit mit der Formel:
$relative Häufigkeit = \frac{absolute Häufigkeit}{Anzahl der Versuche insgesamt}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$2 \cdot (3 x + x^{2}) - 2 x^{2}$	$=$	$x + 10$
	↓	auflösen der Klammer
$6 x + 2 x^{2} - 2 x^{2}$	$=$	$x + 10$
	↓	linke Seite zusammenfassen
$6 x$	$=$	$x + 10$	$- x$
	↓	subtrahieren
$5 x$	$=$	$10$	$: 5$
	↓	dividieren
$x$	$=$	$2$

$(x + 3)^{2} + 4 x =$	$=$	$(x + 3) \cdot (x + 3) + 4 x$
	↓	ausmultiplizieren der Klammer
	$=$	$x^{2} + 6 x + 9 + 4 x$
	↓	zusammenfassen
	$=$	$x^{2} + 10 x + 9$

$15$	$=$	$2 b + b$
	↓	zusammenfassen
$15$	$=$	$3b$	$: 3$
	↓	dividieren und Seiten tauschen
$b$	$=$	$5$

$\frac{1}{2}$	$=$	$\frac{6}{x - 2}$	$(x - 2)$
	↓	multipliziere
$\frac{x - 2}{2}$	$=$	$6$	$\cdot 2$
	↓	multipliziere
$x - 2$	$=$	$12$	$+ 2$
	↓	addiere
$x$	$=$	$14$

2023

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösen der Gleichung: 2⋅(3x+x2)–2x2=x+10

Auflösen der Klammer und zusammenfassen:

Berechnen der Koordinaten des Punktes B(x|y)

Lösen der Gleichung: $2 \cdot (3 x + x^{2}) – 2 x^{2} = x + 10$

Berechnen der Koordinaten des Punktes $B (x | y)$