2024

1
Kreuze die richtige Geradengleichung zur abgebildeten Gerade $g$ an.
( 1 Pkt.)
$y = - \frac{2}{3} x$
$y = \frac{2}{3} x$
$y = - \frac{3}{2} x$
$y = \frac{3}{2} x$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung und Steigungswinkel
Ankreuzen der Geradengleichung, die zur Geraden $𝐠$ passt.
Die Steigungsfaktor der Geraden $g$ , beträgt, $\frac{2}{3}$ .
(Siehe Skizze.)
Kreuze entsprechend an.
Die Skizze braucht nicht erstellt zu weren.
2
Die Funktion $h$ hat die Gleichung $h : y = x - 4$ . Ermittle die Nullstelle $x_{0}$ der Funktion $h$ .
$x_{0} =$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichung
Ermitteln der Nullstelle $𝐱_{𝟎}$ der Funktion $𝐡$ .
setze y=0
↓
$x - 4$ $=$ $0$ $+ 4$
↓
addiere
$x$ $=$ $4$
$x_{0} = 4$
Setze $y = 0$ .
Löse die Gleichung nach $x$ auf.
3
Gegeben sind Gleichungen von Ursprungsgeraden. Welches der 5 Paare beschreibt
Ursprungsgeraden, die aufeinander senkrecht stehen?
Kreuze an.
( 1 Pkt.)
$\begin{array}{l} g_{1} : y = 2 x \\ h_{1} : y = - 2 x \end{array}$
$\begin{array}{l} g_{2} : y = - \frac{1}{3} x \\ h_{2} : y = - 3 x \end{array}$
$\begin{array}{l} g_{3} : y = \frac{1}{4} x \\ h_{3} : y = 4 x \end{array}$
$\begin{array}{l} g_{4} : y = \frac{1}{5} x \\ h_{4} : y = - 5 x \end{array}$
$\begin{array}{l} g_{5} : y = \frac{6}{7} x \\ h_{5} : y = \frac{7}{6} x \end{array}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
Bestimmen der Ursprungsgeraden, die senkrecht aufeinander stehen.
Falls $m_{1} \cdot m_{2} = - 1$ ist, so stehen die Geraden senkrecht aufeinander.
Prüfen, bei welchem der 5 Paare das zutrifft.
$g_{n}$
$h_{n}$
$m_{g_{n}}$
$m_{h_{n}}$
$m_{g_{n}} \cdot m_{h_{n}}$
1
1
$2$
$- 2$
$- 4$
2
2
$- \frac{1}{3}$
$- 3$
$1$
3
3
$\frac{1}{4}$
$4$
$1$
4
4
$\frac{1}{5}$
$- 5$
$-𝟏$
5
5
$\frac{6}{7}$
$\frac{7}{6}$
$1$
Die Geraden $g_{4}$ und $h_{4}$ stehen senkrecht aufeinander.
Kreuze entsprechend an.
4
Ergänze die fehlenden Terme in den Kästchen so, dass eine wahre Aussage bei
Anwendung des Distributivgesetzes entsteht.
$5 a b \cdot (3 a – 6 b^{2} +)$ = $– 30 a b^{3} + 5 a b$
( 2 Pkt.)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Distributivgesetz
Ergänzen der fehlenden Terme.
Berechnen des 1. Terms:
$5 a b \cdot 1. T e r m = 5 a b \Rightarrow 1. T e r m = 𝟏$
Berechnen des 2. Terms:
$5 a b \cdot 3 a = 2. T e r m \Rightarrow 2. T e r m = 𝟏𝟓𝐚²𝐛$
Ergänzte Terme.
$5 a b \cdot (3 a – 6 b^{2} + 𝟏) = 𝟏𝟓𝐚²𝐛 – 30 a b^{3} + 5 a b$
5
Nur für eine der folgenden Kombinationen von Bestimmungsstücken existiert
ein Dreieck $ABC$ .
( 1 Pkt.)
$a = 3 cm, b = 5 cm u n d c = 9 cm$
$a = 7 cm, b = 4 cm u n d α = 100 °$
$α = β = 90 ° u n d c = 4 cm$
$α = 45 °, β = 75 °, γ = 50 °$
$α = β = γ = 65 °$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreiecke konstruieren
Ermitteln der Kombination von Bestimmungsstücken, für die ein Dreieck $ABC$ existiert.
$a = 3 cm, b = 5 cm u n d c = 9 cm$ Dreieck existiert nicht!
Da die Länge einer Dreiecksseite immer kleiner sein muss als die Summe der Längen der anderen beiden Seiten.
$a = 7 cm, b = 4 cm u n d α = 100 °$ Dreieck existiert!
$α = β = 90 ° u n d c = 4 cm$ Dreieck existiert nicht!
Es gibt kein Dreieck mit zwei rechten Winkeln..
$α = 45 °, β = 75 °, γ = 50 °$ Dreieck existiert nicht!
Da die Winkelsumme aller Innenwinkel im Dreieck immer $180 °$ beträgt .
$α = β = γ = 65 °$ Dreieck existiert nicht!
Da die Winkelsumme aller Innenwinkel im Dreieck immer $180 °$ beträgt .
Kreuze entsprechend an.
6
Gib die Lösungsmenge L der Gleichung an. $x^{2} + 2 x + 1 = - (x + 2) + x^{2}$
$L = {}$
( 1 Pkt.)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungen
Lösungsmenge $𝐋$ der Gleichung.
Lösen der Gleichung.
↓
$x^{2} + 2 x + 1$ $=$ $– (x + 2) + x^{2}$
↓
beseitigen der Klammer
$x^{2} + 2 x + 1$ $=$ $- x - 2 + x^{2}$ $- x^{2}$
↓
subtrahieren
$2 x + 1$ $=$ $- x - 2$ $+ (x - 1)$
↓
addieren
$3 x$ $=$ $- 3$ $: 3$
↓
dividieren
$x$ $=$ $- 1$
$L = {- 1}$
Löse die Gleichung nach x auf.
7
Für ein Parallelogramm $ABCD$ gilt: $a = 5 c m, d = 3 c m$ und $α = 50 °$ .
Vervollständige die Strecke $AB$ zum Parallelogramm $ABCD$ .
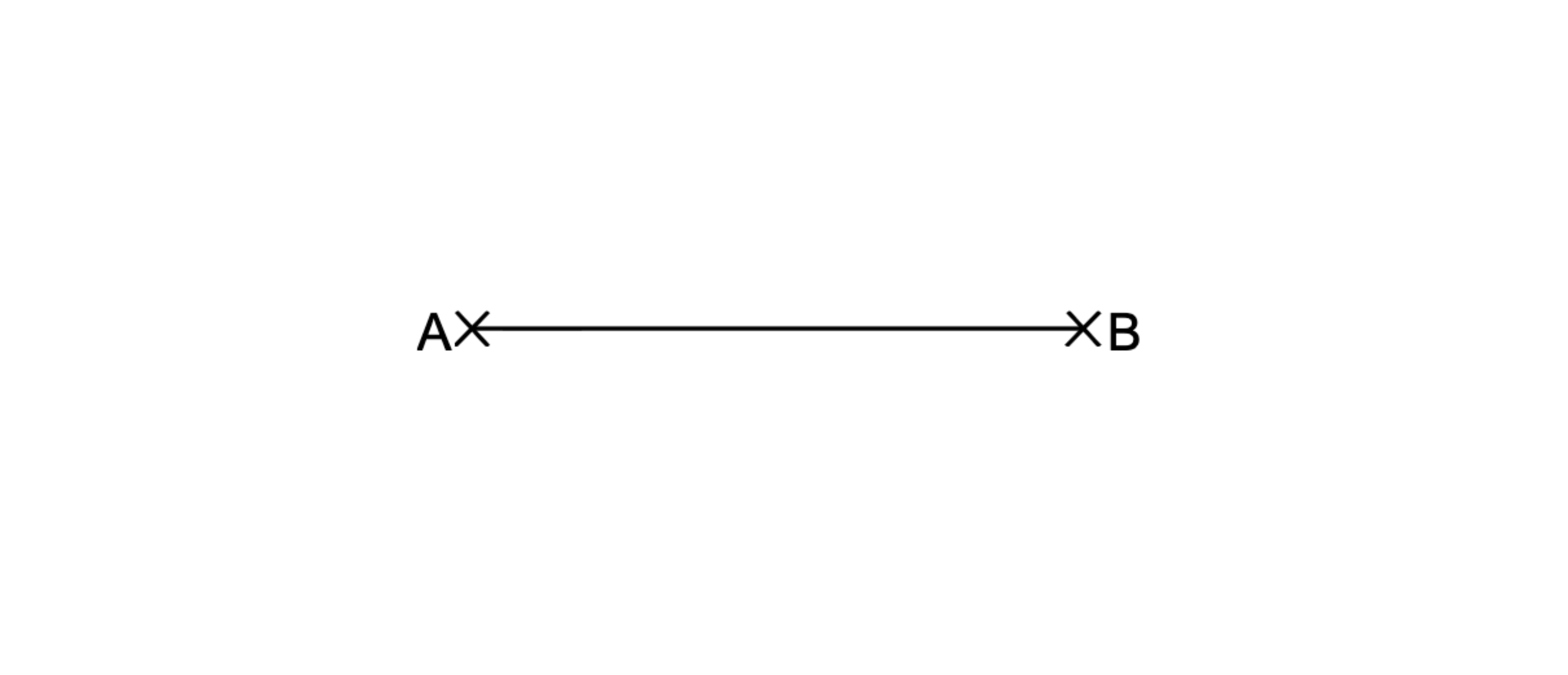
( 1 Pkt.)
8
Löse die Klammern auf und fasse so weit wie möglich zusammen.
$(x + 3)^{2} + (x – 3) (x + 3) =$
( 1 Pkt.)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vereinfachen von Termen mit Klammern
Auflösen der Klammern und zusammenfassen.
$(x + 3)^{2} + (x – 3) (x + 3) =$
$x^{2} + 6 x + 9 + x^{2} - 9 =$
$2 x^{2} + 6 x$
9
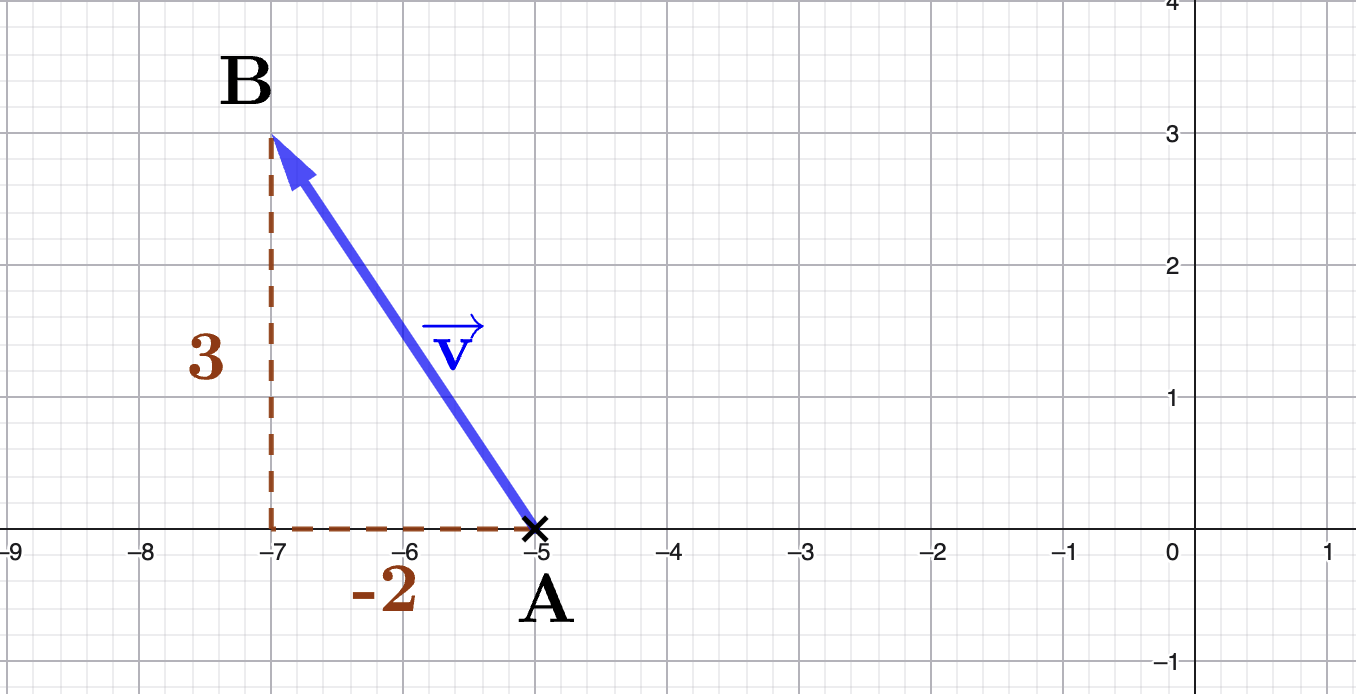
Der Pfeil $\vec{AB}$ ist ein Repräsentant des Vektors $\vec{v}$ .
Dabei gilt: $A (- 5 | 0), B (- 7 | 3)$ .
Gib die Koordinaten des Vektors $\vec{v}$ an.
$\vec{v} = ()$
(1 Pkt.)
10
Der Flächeninhalt $A$ von Rechtecken $A_{n} B_{n} C_{n} D_{n}$ lässt sich in Abhängigkeit von $x$ wie folgt beschreiben: ⁣ $A (x) = [– 2 \cdot (x – 3)^{2} + 50] {cm}^{2}$ .
Von diesen Rechtecken hat $A_{0} B_{0} C_{0} D_{0}$ den größtmöglichen Flächeninhalt $A_{m a x}$ .
Gib diesen an.
$A_{m a x} =$
( 1 Pkt.)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
Angeben des größtmöglichen Flächeninhalts $A_{m a x}$ .
Die Funktion $A (x)$ liegt in der Scheitelform vor.
Die allgemeine Scheitelform lautet:
$f (x) = a (x - x_{s})^{2} + y_{s}$
Folgende Größen sind bekannt:
$a=-2 x_{s} = 3 y_{s} = 50$
Da der Öffnungsfaktor $a < 0$ ist, ist die Parabel nach unten geöffnet.
Bei einer nach unten geöffneten Parabel ist der Funktionswert des Scheitels, der
größtmögliche Wert, den die Funktion annehmen kann.
Der größtmögliche Flächeninhalt ist dann:
$A_{m a x} = 50 {cm}^{2}$
11
Ein kleines Quadrat mit der Seitenlänge $2 cm$ liegt so in einem größeren Quadrat mit der Seitenlänge $8 cm$ , dass alle Eckpunkte auf den Diagonalen des großen Quadrats liegen (siehe Zeichnung).
Ergänze den Flächeninhalt $A$ der schraffierten Fläche.
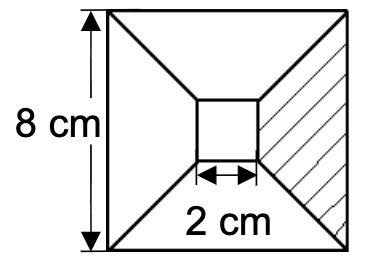
Die Skizze ist nicht maßtreu.
Der Flächeninhalt A der schraffierten Fläche beträgt cm².
( 1 Pkt.)
12
Tamara hat zur Berechnung des Flächeninhalts $A$ eines Dreiecks $PQR$ den folgenden Ansatz aufgestellt:
$A = \frac{1}{2} \cdot | \begin{array}{cc} 2 & 1 \\ - 2 & 3 \end{array} | F E$
Berechne den Flächeninhalt $A$ des Dreiecks $PQR$ .
Der Flächeninhalt beträgt $FE$
( 1 Pkt.)
13
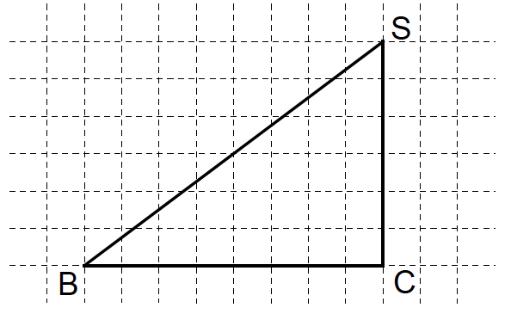
Die Pyramide ABCDS hat die quadratische Grundfläche $ABCD$ und die Höhe $CS$ .
Für das Schrägbild der Pyramide gilt: $ω = 45 °$ , $q = 0,5$ .
$AB$ liegt auf der Schrägbildachse.
Zeichne das Dreieck $BCS$ in wahrer Größe.
( 1 Pkt.)
14
Gegeben ist der Term $T (x) = \frac{x}{x + 3}$ mit der Definitionsmenge $D = ℚ \ {- 3}$ .
Erläutere, warum für diesen Bruchterm eine Definitionsmenge angegeben werden muss.
( 1 Pkt.)
15
Gib die Lösungsmenge $L$ der Bruchgleichung $\frac{1}{x} = \frac{1}{6 - x}$ mit $D = ℚ \ {0; 6}$ an.
$L = {}$
( 1 Pkt.)

$g_{n}$	$h_{n}$	$m_{g_{n}}$	$m_{h_{n}}$	$m_{g_{n}} \cdot m_{h_{n}}$
1	1	$2$	$- 2$	$- 4$
2	2	$- \frac{1}{3}$	$- 3$	$1$
3	3	$\frac{1}{4}$	$4$	$1$
4	4	$\frac{1}{5}$	$- 5$	$-𝟏$
5	5	$\frac{6}{7}$	$\frac{7}{6}$	$1$

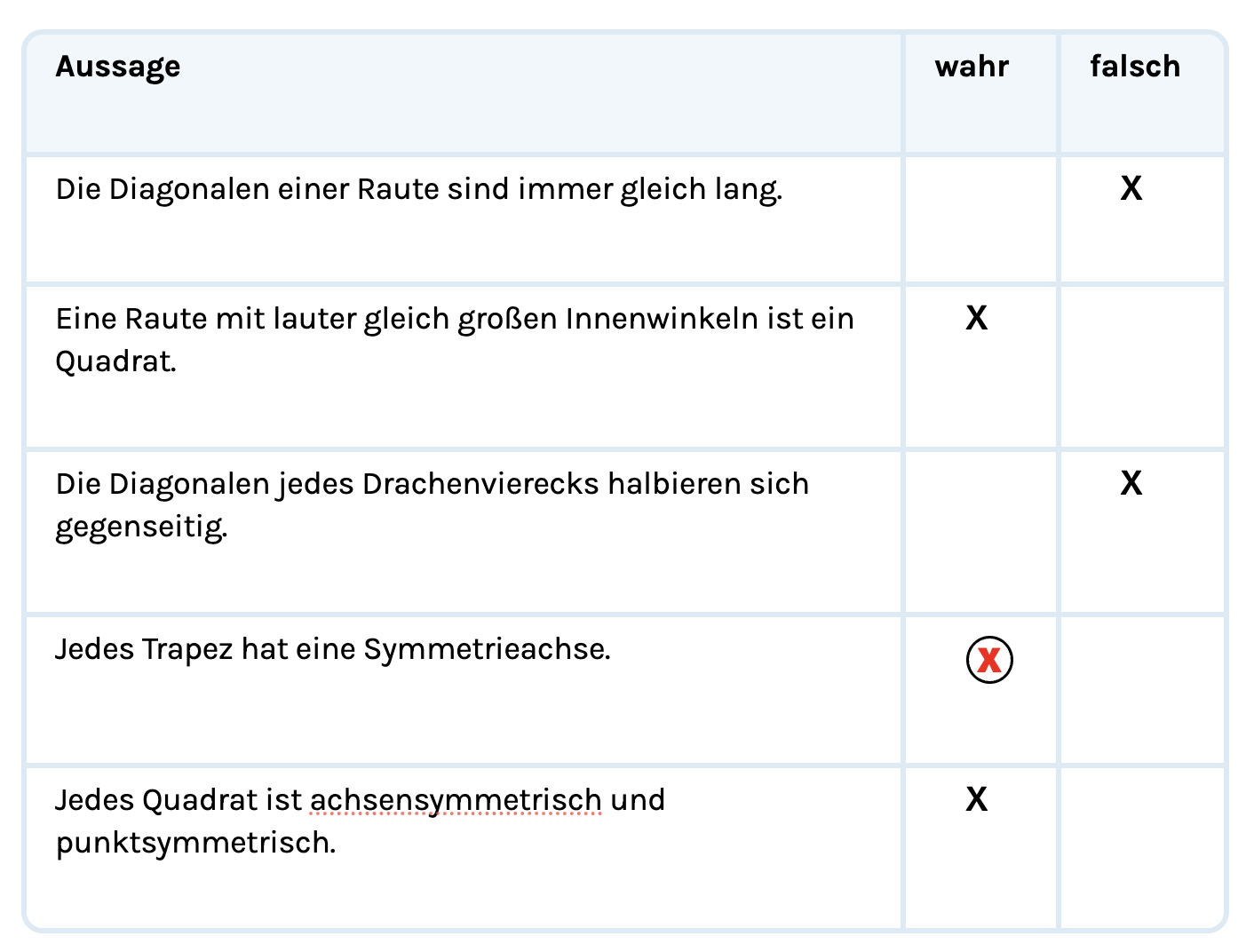
Paul hat Aussagen zu Vierecken beurteilt. Dabei ist ihm ein Fehler unterlaufen.

Markiere das Kreuz, das Paul nicht richtig gesetzt hat.

Aussage	wahr	falsch
Die Diagonalen einer Raute sind immer gleich lang.		$x$
Eine Raute mit lauter gleich großen Innenwinkeln ist ein Quadrat.	$x$
Die Diagonalen jedes Drachenvierecks halbieren sich gegenseitig.		$x$
Jedes Trapez hat eine Symmetrieachse.	$x$
Jedes Quadrat ist achsensymmetrisch und punktsymmetrisch.	$x$

( 1 Pkt.)

17
Ein Raum mit rechteckiger Grundfläche ist $5 m$ lang, $4 m$ breit und $2 m$ hoch.
Der Raum ist komplett mit Luft gefüllt.
Wie viele Kubikmeter Sauerstoff befinden sich im Raum, wenn in der Luft $20 %$ Sauerstoff enthalten sind?
Berechne.
Es befinden sich $m^{3}$ Sauerstoff im Raum
( 1 Pkt.)
18
Marcus ist ein leidenschaftlicher Läufer und joggt jeden Sonntag eine Runde um den See. Dabei hat er 3 Routen zur Wahl:
Bestimme die ungefähre Länge der Route $C$ mithilfe der maßstabsgetreuen Abbildungen.
Gib deinen Lösungsweg an.
Die Route C ist ca. $km$ lang.
( 1 Pkt.)
19
Das Kreisdiagramm soll das Ergebnis der Schülersprecherwahl einer bayerischen Realschule zeigen. Bei der Wahl wurden $720$ gültige Stimmen abgegeben. Die Anteile von Luca und Marie wurden schon eingetragen. Kevin konnte die Wahl mit $240$ Stimmen für sich entscheiden, die restlichen Stimmen erhielt Nina.
Vervollständige das Kreisdiagramm.
( 1 Pkt.)
20
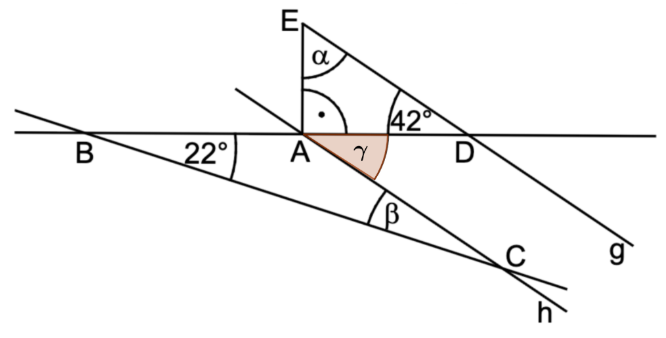
Gib die Winkelmaße $α$ und $β$ an.
Es gilt:
$g | | h$
Die Skizze ist nicht maßtreu.
$α = °$
$β = °$
( 1 Pkt.)
21
Mia hat mit einem 6-seitigen Würfel ein Zufallsexperiment durchgeführt und ihre
Beobachtungen notiert. Sie soll damit die absolute Häufigkeit des Ereignisses $E$
„Die gewürfelte Zahl ist gerade.“ bestimmen.
Gib die absolute Häufigkeit des Ereignisses $E$ an.
Die absolute Häufigkeit des Ereignisses $E$ beträgt .
( 1 Pkt.)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Lösen der Gleichung.
	↓
$x^{2} + 2 x + 1$	$=$	$– (x + 2) + x^{2}$
	↓	beseitigen der Klammer
$x^{2} + 2 x + 1$	$=$	$- x - 2 + x^{2}$	$- x^{2}$
	↓	subtrahieren
$2 x + 1$	$=$	$- x - 2$	$+ (x - 1)$
	↓	addieren
$3 x$	$=$	$- 3$	$: 3$
	↓	dividieren
$x$	$=$	$- 1$

2024

Ankreuzen der Geradengleichung, die zur Geraden 𝐠 passt.

Ermitteln der Nullstelle 𝐱𝟎 der Funktion 𝐡.

Bestimmen der Ursprungsgeraden, die senkrecht aufeinander stehen.

Ergänzen der fehlenden Terme.

Ermitteln der Kombination von Bestimmungsstücken, für die ein Dreieck ABC existiert.

Lösungsmenge 𝐋 der Gleichung.

Auflösen der Klammern und zusammenfassen.

Angeben des größtmöglichen Flächeninhalts Amax.

Ankreuzen der Geradengleichung, die zur Geraden $𝐠$ passt.

Ermitteln der Nullstelle $𝐱_{𝟎}$ der Funktion $𝐡$ .

Ermitteln der Kombination von Bestimmungsstücken, für die ein Dreieck $ABC$ existiert.

Lösungsmenge $𝐋$ der Gleichung.

Angeben des größtmöglichen Flächeninhalts $A_{m a x}$ .