Aufgaben zur Kurvendiskussion - lernen mit Serlo!

Führe für jede Funktion jeweils eine vollständige Kurvendiskussion durch und zeichne die Graphen der Funktionen in ein geeignetes Koordinatensystem.

Folgende Aspekte werden in einer Kurvendiskussion untersucht:

Definitionsbereich
Nullstellen
Symmetrieverhalten
Extrem- und Wendepunkte
Grenzwerte
Monotonie

$f (x) = x^{3} - x^{2} - x + 1$

Definitionsbereich festlegen
Artikel zum Thema
Da die Funktion keine Brüche , Wurzeln oder Logarithmen mit $x$ enthält, die den Definitionsbereich einschränken könnten, lautet der Definitionsbereich der Funktion $D_{f} = R D_f=ℝ$ .
$f\left(x\right)=x^3-x^2-x+1$
Um die Nullstellen von $f\left(x\right)$ zu bestimmten, wird $f\left(x\right)=0$ gesetzt.
$x^{3} - x^{2} - x + 1 = 0$
Die erste Nullstelle muss erraten werden.
$f (1) = 1^{3} - 1^{2} - 1 + 1 = 0$
$\;\;\Rightarrow\;\;{\mathrm{NS}}_1\left(1\vert0\right)$
Ermittle die restlichen Nullstellen, da es sich um ein Polynom dritten Grades handelt, mit der Polynomdivision.
Polynomdivision
Artikel zum Thema
$\def\arraystretch{1.25} \begin{array}{l}\;\;\left(x^3-x^2-x+1\right)\div\left(x-1\right)=x^2-1\\\underline{-\left(x^3-x^2\right))\;\;\;\;\;\;}\\\;\;\;\;\;\;\;\;\;\;-x+1\\\;\;\;\;\;\;\;\underline{-\left(-x+1\right)\;\;\;}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\end{array}$
Setze die erhaltene Funktion gleich 0.
$x^{2} - 1 = 0$
$x^{2} = 1$
Ziehe die Wurzel aus $x^{2}$ und $1$ .
$\sqrt{x^2}=\sqrt1$
$\;\;\Rightarrow\;\;x_2=1$
$\;\;\Rightarrow\;\;x_3=-1$
Symmetrieverhalten
Artikel zum Thema
Durch Betrachtung
Die Exponenten zur Basis $x$ sind sowohl gerade als auch ungerade.
$\;\;\Rightarrow\;\;$ Der Graph ist weder achsen- noch punktsymmetrisch zum Ursprung.
Durch Berechnung
Prüfen ob $f (x) = f (- x)$
Hiermit wird geprüft ob der Graph achsensymmetrisch zur y-Achse verläuft
$x^3-x^2-x+1=\left(-x\right)^3-\left(-x\right)^2-\left(-x\right)+1$
$x^3-x^2-x+1\;\neq\;-x^3-x^2+x+1$
Der Graph ist nicht achsensymmetrisch, da $f\left(x\right)\ne f\left(-x\right)$ .
Prüfen ob $f (- x) = - f (x)$
Hiermit wird geprüft ob der Graph punktsymmetrisch zum Ursprung verläuft.
$\left(-x\right)^3-\left(-x\right)^2-\left(-x\right)+1=-\left(x^3-x^2-x+1\right)$
$-x^3-x^2+x+1\neq-x^3+x^2+x-1$
Der Graph ist nicht punktsymmetrisch, da $f(-x)\ne-f(x)$ .
Ableitungen
Artikel zum Thema
Erste Ableitung
$f (x) = x^{3} - x^{2} - x + 1$
$f^{'} (x) = 3 x^{2} - 2 x - 1$
Zweite Ableitung
Die erste Ableitung von $f (x)$ ist Ausgangspunkt für die zweite Ableitung.
$f^{''} (x) = 6 x - 2$
Dritte Ableitung
$f^{'''} (x) = 6$
Extrema bestimmen
Artikel zum Thema
$f^{'} (x) = 0$
Die Extrema der Funktion sind die Nullstellen der ersten Ableitung.
$3x^2-2x-1\;=\;0$
Da $f^{'} (x)$ ein Polynom zweiten Grades ist, können seine Nullstellen mithilfe der Mitternachtsformel bestimmt werden.
$x_{1{,}2}=\dfrac{-(-2)\pm\sqrt{(-2)^2-4\cdot3\cdot(-1)}}{2\cdot3}$
$x_{1{,}2}=\dfrac{2\pm\sqrt{4-(-12)}}6$
$x_{1{,}2}=\dfrac{2\pm\sqrt{4+12}}6=\dfrac{2\pm\sqrt{16}}6$
$x_{1{,}2}=\frac{2\pm4}6$
$x_1=\frac{2+4}6=\frac66=1$
Der erste $x$ -Wert, der in die erste Ableitung der Funktion $f (x)$ eingesetzt 0 ergibt.
$x_2=\frac{2-4}6=\frac{-2}6=-\frac13$
Der zweite $x$ -Wert, der in die erste Ableitung der Funktion $f (x)$ eingesetzt 0 ergibt.
1. Extremum
Artikel zum Thema
$f\left(x\right)=x^3-x^2-x+1$
$x$ -Wert des ersten gefundenen Extrempunkts in die Ausgangsfunktion einsetzen.
$f\left(1\right)=1^3-1^2-1+1=1-1-1+1=0$
$f\left(1\right)=0$
Untersuchen ob Hoch- oder Tiefpunkt
$f''\left(x\right)=6x-2$
$f''\left(1\right)=6\cdot1-2=4$
Da $f''\left(2\right)>0$ hat $f\left(x\right)$ an der Stelle $\left(1\vert0\right)$ einen Tiefpunkt .
$\;\;\Rightarrow\;\;\mathrm{TP}\left(1\vert0\right)$
2. Extremum
Artikel zum Thema
$f\left(x\right)=x^3-x^2-x+1$
$x$ -Wert des zweiten gefundenen Extrempunkts in die Ausgangsfunktion einsetzen.
$f\left(-\frac13\right)=\left(-\frac13\right)^3-\left(-\frac13\right)^2-\left(-\frac13\right)+1$
$\;\;\;\;f\left(-\frac13\right)=-\frac1{27}-\frac19+\frac13+1$
Bilde den gemeinsamen Nenner der Summanden .
$\;\;\;\;f\left(-\frac13\right)=-\frac1{27}-\frac{1\cdot3}{9\cdot3}+\frac{1\cdot9}{3\cdot9}+\frac{1\cdot27}{1\cdot27}$
$\;\;\;\;f\left(-\frac13\right)=-\frac1{27}-\frac3{27}+\frac9{27}+\frac{27}{27}$
$\;\;\;\;f\left(-\frac13\right)=\frac{32}{27}$
Untersuchen ob Hoch- oder Tiefpunkt
$f''\left(x\right)=6x-2$
$f''\left(-\frac13\right)=6\cdot\left(-\frac13\right)-2=-4$
Da $f''\left(-\frac{1}{3}\right)<0$ hat $f\left(x\right)$ an der Stelle $\left(-\frac{1}{3}\vert\frac{32}{27}\right)$ einen Hochpunkt .
$\;\;\Rightarrow\;\;\mathrm{HP}\left(-\frac13\vert\frac{32}{27}\right)$
Wendepunkte bestimmen
Artikel zum Thema
$f''\left(x\right)=6x-2$
Wegen $f'''(x)=6\neq 0$ ist die Bedingung immer erfüllt.
$f''\left(x\right)=0$
$6 x - 2 = 0$
$6 x = 2$
$\;\;\Rightarrow\;\;$ $x=\frac26=\frac13$
Wendepunkt $x=\frac13$
$f\left(x\right)=x^3-x^2-x+1$
Gefundenes $x$ aus der Nullsetzung der zweiten Ableitung in $f\left(x\right)$ einsetzen.
$f\left(\frac13\right)=\left(\frac13\right)^3-\left(\frac13\right)^2-\frac13+1$
$f\left(\frac13\right)=\frac1{27}-\frac19-\frac13+1$
Bilde einen gemeinsamen Nenner für alle Summanden.
$f\left(\frac13\right)=\frac1{27}-\frac3{27}-\frac9{27}+\frac{27}{27}$
$f\left(\frac13\right)=\frac{16}{27}$
$\;\;\Rightarrow\;\;\mathrm{WP}\left(\frac13\vert\frac{16}{27}\right)$
Erster und einziger Wendepunkt der Funktion gefunden bei $\left(\frac13\vert\frac{16}{27}\right)$
Grenzwertbetrachtung
Artikel zum Thema
$D_{f} = R D_f=ℝ$
Da die Funktion keine Definitionslücken hat, muss nur das Verhalten gegen $\pm\infty$ betrachtet werden.
Bei Polynomen wird der Grenzwert bei $\pm \infty$ durch den Summanden mit dem höchsten Exponenten bestimmt:
$\displaystyle\lim_{x\rightarrow\infty}x^3=\infty$
und
$\displaystyle\lim_{x\rightarrow-\infty}x^3=-\infty$
Daher ist $\displaystyle\lim_{x\to\infty} f(x)=\infty$ und $\displaystyle\lim_{x\to-\infty}f(x)=-\infty$ .
Monotonieverhalten
Artikel zum Thema
Die Monotonie der Funktion wird mithilfe einer Tabelle bestimmt.
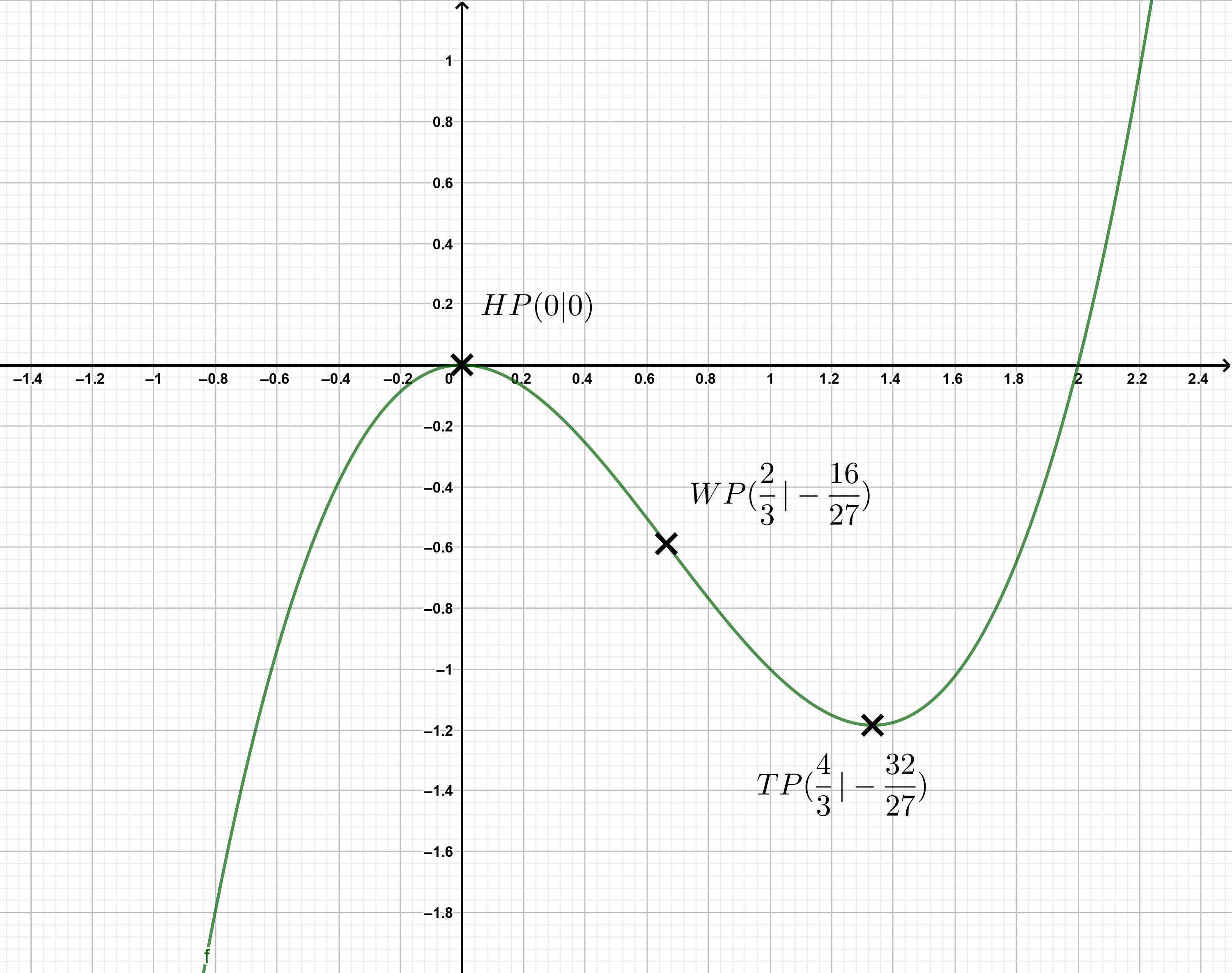
Graph
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

$f (x) = 2 x^{4} - 4 x^{2} + 1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ganzrationale Funktionen (Polynomfunktionen)

Definitionsbereich bestimmen

Da die Funktion ganzrational ist und keine Wurzeln oder Logarithmen aufweist, lautet der Definitionsbereich der Funktion $D_{f} = R D_f=ℝ$ .

Nullstellenbestimmung

Setze $f (x)$ gleich $0$ , um die Nullstellen von $G_{f}$ zu bestimmen.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle 2x^4-4x^2+1$	$=$	$\displaystyle 0$

Bei dieser Gleichung findet man durch das systematische Einsetzen von ganzzahligen Werten keine Nullstelle. Durch Substitution allerdings lässt sich aus der biquadratischen Gleichung ein Polynom zweiten Grades formen. Bei der Substitution wird in einem Term ein Teil (z.B. $x^{2}$ ) durch einen neuen Term (z.B. u) ersetzt.

$x^2=u\;\Rightarrow\;f(u)=2u^2-4u+1$

Setze nun $f (u) = 0$ :

$2 u^{2} - 4 u + 1 = 0$

Zur Lösung dieser Gleichung verwendest du die Mitternachtsformel.

Lies die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein:

$a = 2$ , $b = - 4$ und $c = 1$

$\displaystyle u_{1{,}2}$	$=$	$\displaystyle \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
	↓	Setze $a = 2$ , $b = - 4$ und $ c = 1$ ein.
	$=$	$\displaystyle \dfrac{-(-4)\pm \sqrt{(-4)^{2}-4\cdot2 \cdot 1}}{2\cdot 2}$
	$=$	$\displaystyle \dfrac{4\pm \sqrt{16-8}}{4}$
	$=$	$\displaystyle \dfrac{4\pm \sqrt{8}}{4}$

Du hast die beiden Lösungen

$u_1=\dfrac{4+\sqrt{8}}{4} =1+\dfrac{\sqrt{8}}{4}=1+\sqrt{0{,}5}$

und $u_2=\dfrac{4-\sqrt{8}}{4} =1-\dfrac{\sqrt{8}}{4}=1-\sqrt{0{,}5}$ erhalten.

Resubstitution:

Die Resubstitution beschreibt das Rückgängigmachen der Substitution.

Setze also $x^2=u\;\Rightarrow\;$ $x^2= 1+\sqrt{0{,}5}$ bzw. $x^2=1-\sqrt{0{,}5}$ und löse nach $x$ auf.

$\displaystyle x^2$	$=$	$\displaystyle 1+\sqrt{0{,}5}$	$\displaystyle \sqrt{}$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle \pm\sqrt{1+\sqrt{0{,}5}}$
	$\approx ≈$	$\displaystyle \pm 1{,}31$

$\displaystyle x^2$	$=$	$\displaystyle 1-\sqrt{0{,}5}$	$\displaystyle \sqrt{}$
$\displaystyle x_{3{,}4}$	$=$	$\displaystyle \pm\sqrt{1-\sqrt{0{,}5}}$
	$\approx ≈$	$\displaystyle \pm 0{,}54$

Der Graph der Funktion $f$ hat also insgesamt vier Nullstellen:

$N_1(1{,}31|0),\quad N_2(-1{,}31|0),\quad N_3(0{,}54|0),\quad N_4(-0{,}54|0)$

Ableitungen

$f\left(x\right)=2x^4-4x^2+1$

Erste Ableitung:

$f^{'} (x) = 8 x^{3} - 8 x$

Zweite Ableitung:

$f^{''} (x) = 24 x^{2} - 8$

Extrema

Setze die erste Ableitung der Funktion gleich $0$ , um die Extrema von $G_{f}$ zu bestimmen.

$\displaystyle f'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle 8x^3-8x$	$=$	$\displaystyle 0$
	↓	$x$ ausklammern
$\displaystyle x\cdot\left(8x^2-8\right)$	$=$	$\displaystyle 0$

Du hast die Gleichung $x\cdot\left(8x^2-8\right)=0$ erhalten, die du mit dem Satz vom Nullprodukt lösen kannst.

$x_{1} = 0$ oder $8 x^{2} - 8 = 0$

$\displaystyle 8x^2-8$	$=$	$\displaystyle 0$	$\displaystyle +8$
$\displaystyle 8x^2$	$=$	$\displaystyle 8$	$\displaystyle :8$
$\displaystyle x^2$	$=$	$\displaystyle 1$

Die Gleichung $x^{2} = 1$ hat die beiden Lösungen $x_{2} = 1$ und $x_{3} = - 1$

1. Extremum

Zur Bestimmung des $y$ -Werts des Extremums muss der erste der gefundenen $x$ -Werte $x_{1} = 0$ in die Ausgangsfunktion eingesetzt werden.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle 2x^4-4x^2+1$
	↓	Setze $x_{1} = 0$ ein.
$\displaystyle f\left(0\right)$	$=$	$\displaystyle 2\cdot 0^4-4\cdot 0^2+1$
	$=$	$\displaystyle 1$

Um herauszufinden, ob der gefundene x-Wert ein Hoch- oder Tiefpunkt ist, wird $x_{1} = 0$ in die zweite Ableitung eingesetzt.

$\displaystyle f''(x)$	$=$	$\displaystyle 24x^2-8$
	↓	Setze $x_{1} = 0$ ein.
$\displaystyle f''(0)$	$=$	$\displaystyle 24\cdot 0^2-8$
	$=$	$\displaystyle -8$

Da $f^{''} (0) < 0$ ist, befindet sich an der Stelle $x = 0$ ein Hochpunkt.

$\Rightarrow\;\mathrm{HP}\left(0|1\right)$

2. Extremum

Zur Bestimmung des $y$ -Werts des Extremums muss der zweite der gefundenen $x$ -Werte $x_{2} = 1$ in die Ausgangsfunktion eingesetzt werden.

$\displaystyle f\left(1\right)$	$=$	$\displaystyle 2\cdot1^4-4\cdot1^2+1$
	$=$	$\displaystyle -1$

Um herauszufinden, ob der gefundene Wert ein Hoch- oder Tiefpunkt ist, wird $x_{2} = 1$ in die zweite Ableitung eingesetzt.

$\displaystyle f''(x)$	$=$	$\displaystyle 24x^2-8$
	↓	Setze $x_{2} = 1$ ein.
$\displaystyle f''(1)$	$=$	$\displaystyle 24\cdot 1^2-8$
	$=$	$\displaystyle 16$

Da $f^{''} (1) > 0$ ist, befindet sich an der Stelle $x = 1$ ein Tiefpunkt.

$\Rightarrow\;TP(1|-1)$

3. Extremum

Zur Bestimmung des $y$ -Werts des Extremums muss der dritte der gefundenen $x$ -Werte $x_{3} = - 1$ in die Ausgangsfunktion eingesetzt werden.

$\displaystyle f\left(-1\right)$	$=$	$\displaystyle 2\cdot(-1)^4-4\cdot(-1)^2+1$
	$=$	$\displaystyle -1$

Um herauszufinden, ob der gefundene Wert ein Hoch- oder Tiefpunkt ist, wird $x_{3} = - 1$ in die zweite Ableitung eingesetzt.

$\displaystyle f''(x)$	$=$	$\displaystyle 24x^2-8$
	↓	Setze $x_{3} = - 1$ ein.
$\displaystyle f''(-1)$	$=$	$\displaystyle 24\cdot (-1)^2-8$
	$=$	$\displaystyle 16$

Da $f^{''} (- 1) > 0$ ist, befindet sich an der Stelle $x = - 1$ ein Tiefpunkt.

$\Rightarrow\;TP(-1|-1)$

Wendepunkte

Bestimme die $x$ -Koordinaten der möglichen Wendepunkte als Nullstellen der zweiten Ableitung:

$f''\left(x\right)=24x^2-8$

Bestimme jetzt die Lösungen von $f''\left(x\right)=0$ :

$\displaystyle 24x^2-8$	$=$	$\displaystyle 0$	$\displaystyle :24$
$\displaystyle x^2-\dfrac{1}{3}$	$=$	$\displaystyle 0$	$\displaystyle +\dfrac{1}{3}$
$\displaystyle x^2$	$=$	$\displaystyle \displaystyle\frac{1}{3}$

Du hast die Gleichung $x^2=\dfrac{1}{3}$ erhalten. Sie hat die beiden Lösungen $x_{1{,}2}=\pm \displaystyle\frac{1}{\sqrt{3}}.$

Es gibt also die Kandidaten für die Wendepunkte $x_1=-\dfrac{1}{\sqrt{3}}$ und $x_2=\dfrac{1}{\sqrt{3}}$ . Wenn an diesen Stellen die dritte Ableitung ungleich Null ist, ist die Bedingung für einen Wendepunkt erfüllt.

Berechne die dritte Ableitung und setze die möglichen Wendestellen ein:

$f^{'''} (x) = 48 x$

\displaystyle f'''\left(\pm\dfrac{1}{\sqrt{3}}\right)

=

\displaystyle \displaystyle\pm\frac{48}{\sqrt{3}}\neq 0

Damit ist die Bedingung erfüllt.

Um die $y$ -Koordinaten zu berechnen, werden die $x$ -Werte in die Funktion $f$ eingesetzt:

$f\left(-\frac{1}{\sqrt3}\right)=2\cdot\left(-\frac{1}{\sqrt3}\right)^4-4\cdot\left(-\frac{1}{\sqrt3}\right)^2+1=\frac{2}{9}-\frac{4}{3}+1=-\frac19$

$f\left(\frac{1}{\sqrt3}\right)=2\cdot\left(\frac{1}{\sqrt3}\right)^4-4\cdot\left(\frac{1}{\sqrt3}\right)^2+1=\frac{2}{9}-\frac{4}{3}+1=-\frac19$

Damit hast du die Wendepunkte berechnet:

${\mathrm{WP}}_1\left(-\sqrt{\frac13}\vert-\frac19\right)\text{bzw.}\;{\mathrm{WP}}_1\left(-\frac{1}{\sqrt{3}}\vert-\frac19\right)$

${\mathrm{WP}}_2\left(\sqrt{\frac13}\vert-\frac19\right)\text{bzw.}\;{\mathrm{WP}}_2\left(\frac{1}{\sqrt{3}}\vert-\frac19\right)$

Grenzwertbetrachtung

$D_{f} = R D_f=ℝ$

Da die Funktion keine Definitionslücken hat, muss nur das Verhalten der Funktion für $x\to\pm\infty$ betrachtet werden.

gegen $+\infty$ :

Bei ganzrationalen Funktionen ist nur die höchste Potenz wichtig, um die Grenzwertbetrachtung durchzuführen.

$\displaystyle\lim_{x\rightarrow\infty}\overset{\rightarrow\infty}{2x^4}-{4x^2}+1=\infty$

gegen $-\infty$ :

$\displaystyle\lim_{x\rightarrow-\infty}\overset{\rightarrow\infty}{2x^4}-{4x^2}+1=\infty$

Symmetrie

Durch Betrachtung des Funktionsterms

Die Exponenten zur Basis $x$ sind alle gerade. Daraus folgt, dass der Graph symmetrisch zur y-Achse verläuft.

Durch Berechnung mit dem Kriterium $f (- x) = f (x)$

$\displaystyle f\left(x\right)$	$=$	$\displaystyle 2x^4-4x^2+1$
$\displaystyle f\left(-x\right)$	$=$	$\displaystyle 2\cdot\left(-x\right)^4-4\cdot\left(-x\right)^2+1$
	$=$	$\displaystyle 2\cdot x^4-4\cdot x^2+1$
$\displaystyle f\left(x\right)$	$=$	$\displaystyle f\left(-x\right)$

Da $f\left(x\right)$ gleich $f\left(-x\right)$ ist, ist der Graph von $f$ achsensymmetrisch zur y-Achse.

Beachte

Wenn du als Erstes die Symmetrie nachweist, kannst du die Koordinaten des dritten Extremums aus denen des zweiten direkt ablesen.

Genauso kannst du den zweiten Wendepunkt aus dem ersten bestimmen und den Grenzwert bei $-\infty$ aus dem Grenzwert bei $\infty$ .

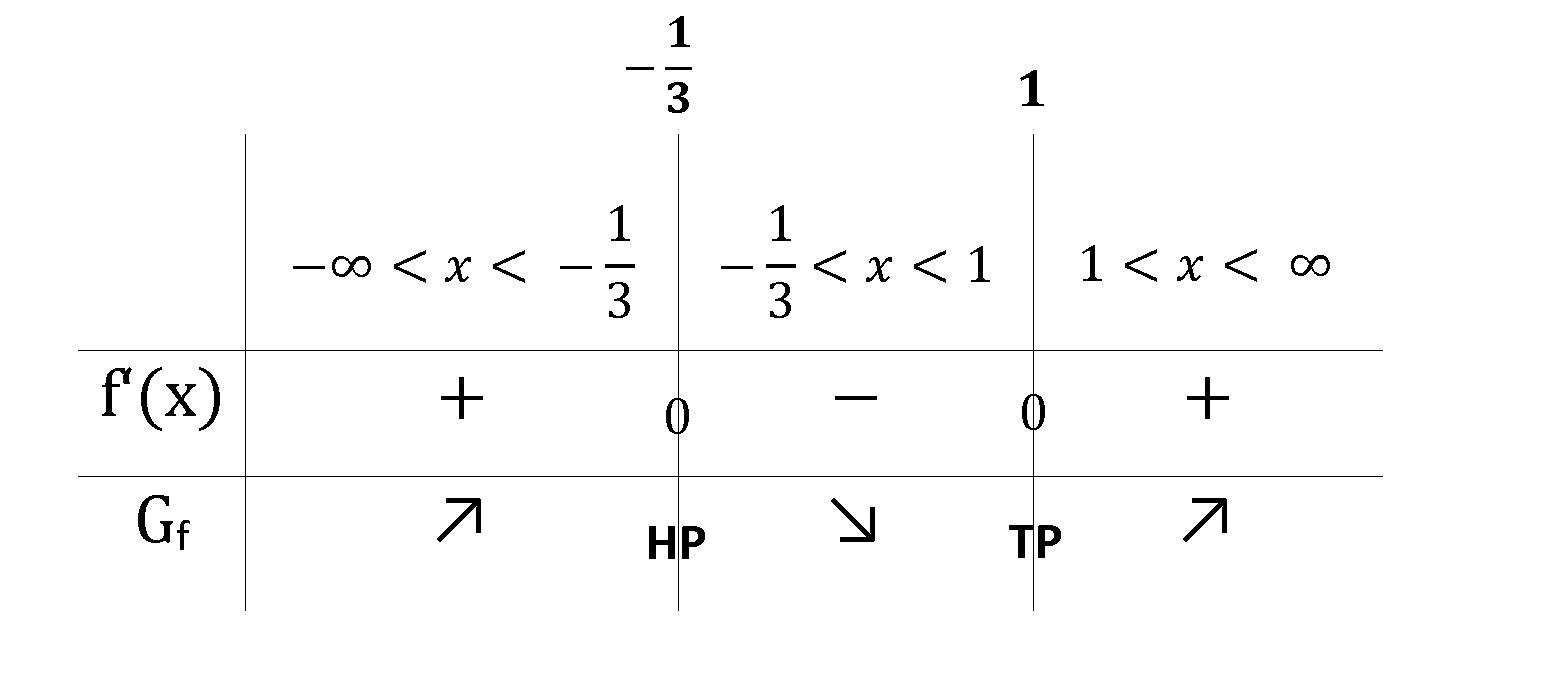
Monotonieverhalten

Die Monotonie wird mit Hilfe einer Tabelle bestimmt.

Graph

Hinweis: Die Schnittpunkte mit der x-Achse sind in der Abbildung in aufsteigender Reihenfolge angegeben (im Gegensatz zur obigen Berechnung).

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$f (x) = x^{3} - 2 x^{2}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Definitionsbereich festlegen
Da die Funktion keine Brüche, Wurzeln oder Logarithmen mit $x$ enthält, die den Definitionsbereich einschränken könnten, lautet der Definitionsbereich der Funktion $\mathbb{D}_f=ℝ$ .
Nullstellenbestimmung
Um die Nullstellen von $f\left(x\right)$ zu bestimmten, wird $f\left(x\right)=0$ gesetzt.
$x^{3} - 2 x^{2} = 0$
Klammere $x^{2}$ aus und betrachte die Faktoren einzeln.
$x^{2} (x - 2) = 0$
$\Rightarrow{\mathrm{NS}}_1\left(0\vert0\right), \mathrm{NS}_2( 2|0)$
Ableitungen
$f\left(x\right)=x^3-2x^2$
Erste Ableitung
$f'\left(x\right)=3x^2-4x$
Zweite Ableitung
$f''\left(x\right)=6x-4$
Extrema
x-Koordinaten bestimmen
$f'\left(x\right)=0$
$3 x^{2} - 4 x = 0$
$x$ ausklammern und die Faktoren einzeln betrachten.
$x (3 x - 4) = 0$
$\Leftrightarrow x=0$ oder $3 x - 4 = 0$
$\Rightarrow x_1=0, x_2=\dfrac{4}{3}$
y-Koordinaten bestimmen
Setze die gefundenen $x$ -Werte in $f$ ein, um die $y$ -Koordinaten der Extrema zu erhalten.
$f\left(x_1\right)=f\left(0\right)=0$
da $0$ eine Nullstelle ist.
$f\left(x_2\right)=f\left(\frac43\right)=\left(\frac43\right)^3-2\cdot\left(\frac43\right)^2=-\frac{32}{27}$
Prüfung auf Hoch- oder Tiefpunkt
$f''\left(x\right)=6x-4$
Setze die gefundenen $x$ -Werte in $f^{''}$ ein, um zu bestimmen, ob es sich bei den Extrema um einen Hoch- oder Tiefpunkt handelt.
$f''\left(x_1\right)=f''\left(0\right)=-4$
$f'' \lt 0\Rightarrow\mathrm{HP}\left(0\vert0\right)$
$f''\left(x_4\right)=f''\left(\frac43\right)=6\cdot\frac43-4=4$
$f''>0 \Rightarrow\mathrm{TP}\left(\frac43\left|-\frac{32}{27}\right)\right.$
Wendepunkt
$f''\left(x\right)=6x-4$
Die zweite Ableitung wird gleich 0 gesetzt, um Wendepunkte zu bestimmen.
x-Koordinate des Wendepunkts
$f''\left(x\right)=0$
$6 x - 4 = 0$
$\Rightarrow x_W=\dfrac46=\dfrac23$
y-Koordinate des Wendepunkts
$f (x) = x^{3} - 2 x^{2}$
Das gefundene $x_{W}$ wird in die Funktion $f$ eingesetzt, um die $y$ -Koordinate des Wendepunkts zu bestimmen.
$f\left(\dfrac23\right)=\left(\dfrac23\right)^3-2\cdot\left(\dfrac23\right)^2=-\dfrac{16}{27}$
$\mathrm{WP}\left(\frac23\left|-\frac{16}{27}\right)\right.$
Grenzwertbetrachtung
$\mathbb{D}_f=ℝ$ . Da die Funktion keine Definitionslücken aufweist, muss nur das Grenzwertverhalten für $x\rightarrow\pm\infty$ untersucht werden.
$\displaystyle\lim_{x\rightarrow\infty}f\left(x\right)=\lim_{x \rightarrow \infty} \overbrace{x^3}^{\rightarrow \infty}-2\cdot \overbrace{x^2}^{\rightarrow \infty}=\infty$
$\lim_{x\rightarrow-\infty}f\left(x\right)=\lim_{x\rightarrow-\infty}\;\overset{\rightarrow-\infty}{\overset︷{x^3}}-2\cdot\overset{\rightarrow+\infty}{\overset︷{x^2}}=-\infty$
Symmetrie
$f\left(x\right)=x^3-2\cdot x^2$
Die Exponenten zur Basis $x$ sind sowohl gerade als auch ungerade. Daraus folgt, dass der Graph weder achsensymmetrisch noch punktsymmetrisch verläuft.
Die Symmetrie kann auch mithilfe des Funktionsterms bestimmt werden:
$f\left(x\right)=x^3-2x^2$
$f\left(-x\right)=-x^3-2\cdot x^2$
Da $f\left(-x\right)$ weder gleich $f\left(x\right)$ noch $-f\left(x\right)$ ist, weist die Funktion keine Symmetrie auf.
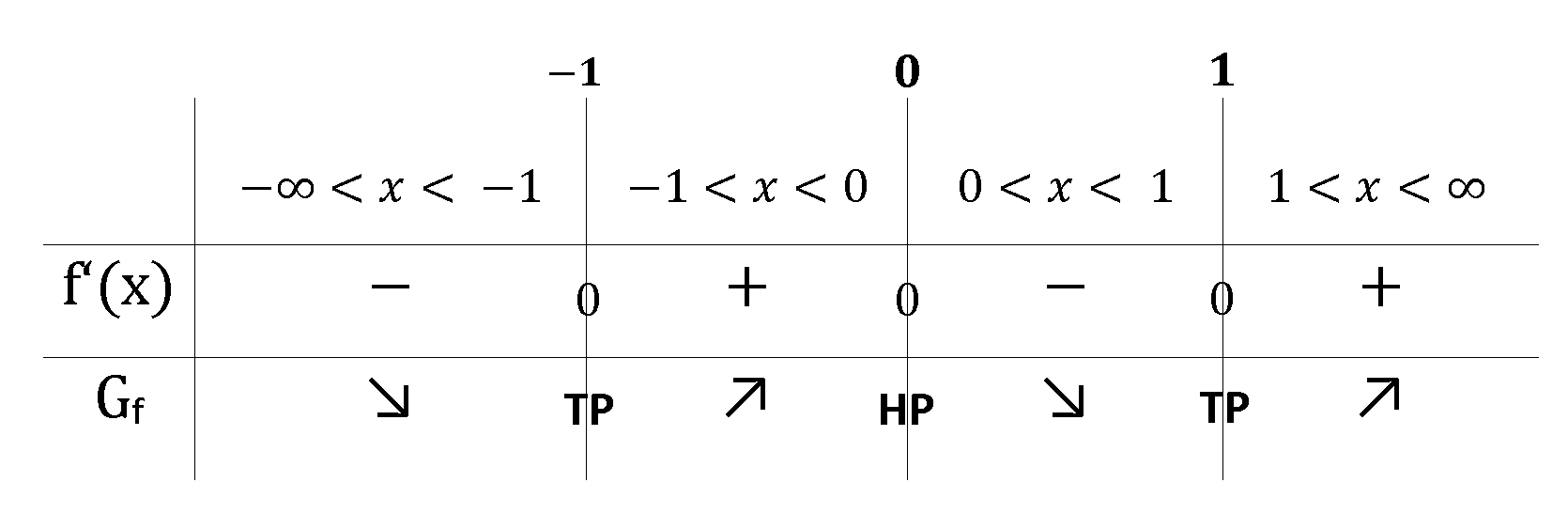
Monotonieverhalten
Die Monotonie wird mithilfe einer Tabelle bestimmt.
Graph
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$f(x)=\frac12x^4-\frac32x^2+2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Definitionsbereich festlegen
Da die Variable der Funktion weder im Nenner eines Bruchs, noch in einem Logarithmusterm oder in einer Diskriminante vorkommt, können in der Funktion keine Definitionslücken vorkommen. Also liegt der Definitionsbereich von $f\left(x\right)$ in ganz $R ℝ$ .
Nullstellenbestimmung
$f(x)=\frac{1}{2}x^4-\frac{3}{2}x^2+2$
Um aus dem Polynom vierten Grades ein Polynom zweiten Grades zu erzeugen, wird das Substitutionsverfahren angewendet. Das funktioniert in diesem speziellen Fall, da der Funktionsterm biquadratisch ist, wie im Beispiel des Artikels Substitution.
$z = x^{2}$
$f\left(x\right)=\frac12z^2-\frac32z+2$
Die Nullstellen von einem Polynom zweiten Grades werden jetzt mit der Mitternachtsformel ermittelt.
$z_{1/2}=\frac{\frac32\pm\sqrt{\frac94-4\cdot\frac12\cdot2}}{2\cdot\frac12}=\frac{\frac32\pm\sqrt{\frac94-\frac{16}4}}1=\frac{\frac32\pm\sqrt{-\frac74}}1$
Da die Diskriminante negativ ist, gibt es keine reellen Nullstellen.
Die Funktion $f\left(x\right)$ hat keine Nullstellen.
Ableitungen
$f\left(x\right)=\frac12x^4-\frac32x^2+2$
Erste Ableitung
$f'\left(x\right)=2x^3-3x$
Zweite Ableitung
$f''\left(x\right)=6x^2-3$
Extrema bestimmen
$f'\left(x\right)=0$
Die erste Ableitung wird gleich $0$ gesetzt.
$2 x^{3} - 3 x = 0$
In dieser Gleichung kann $x$ ausgeklammert werden. $x (2 x^{2} - 3) = 0$ . Mit dem Satz vom Nullprodukt folgt die erste Nullstelle.
$x_{1} = 0$
$2 x^{2} - 3 = 0$ liefert zwei weitere Lösungen:
$x_{2{,}3}=\pm\sqrt{1{,}5}$
$x_2=\sqrt{1{,}5}\approx 1{,}22$
$x_3=-\sqrt{1{,}5}\approx -1{,}22$
1. Extremum $\left(x=0\right)$
$f(x)=\frac12x^4-\frac32x^2+2$
$f\left(0\right)=2$
$f''\left(0\right)=6\cdot0^2-3=-3$
Da $f''\left(0\right)$ kleiner $0$ , befindet sich an der ermittelten Stelle ein Hochpunkt.
$\mathrm{HP}=\left(0\vert2\right)$
2. Extremum $\left(x=\sqrt{1{,}5}\right)$
$f(x)=\frac12x^4-\frac32x^2+2$
$f\left(\sqrt{1{,}5}\right)=\frac78$
$f''\left(\sqrt{1{,}5}\right)=\frac12\cdot\sqrt{1{,}5}^4-\frac32\cdot\sqrt{1{,}5}^2-3$
Da $f''\left(0\right)$ größer $0$ , befindet sich an der ermittelten Stelle ein Tiefpunkt.
$\mathrm{TP}=\left(\sqrt{1{,}5}\vert0{,}875\right)$
3. Extremum $\left(x=-\sqrt{1{,}5}\right)$
$f(x)=\frac12x^4-\frac32x^2+2$
$f\left(-\sqrt{1{,}5}\right)=\frac78$
$f''\left(-\sqrt{1{,}5}\right)=\frac12\cdot\left(-\sqrt{1{,}5}^4\right)-\frac32\cdot\left(-\sqrt{1{,}5}^2\right)-3$
Da $f''\left(0\right)$ größer $0$ , befindet sich an der ermittelten Stelle ein Tiefpunkt.
$\mathrm{TP}=\left(-\sqrt{1{,}5}\vert0{,}875\right)$
Wendepunkt
Die Wendepunkte werden berechnet, indem die zweite Ableitung null gesetzt wird.
$f''\left(x\right)=6x^2-3$
$f''\left(x\right)=0$
$6 x^{2} - 3 = 0$
$\Rightarrow x^2=\frac36=\frac12$
$x_{W_1}=\sqrt{\frac12}\approx 0{,}71$
$x_{W_2}=-\sqrt{\frac12}\approx 0{,}71$
y-Koordinaten bestimmen
$f\left(x_{W_1}\right)=f\left(\sqrt{\frac12}\right)$
$f\left(\sqrt{\frac12}\right)=\frac12\cdot\sqrt{\frac12}^4-\frac32\cdot\sqrt{\frac12}^2+2=1{,}375=\frac{11}8=1\frac38$
$f\left(x_{W_2}\right)=f\left(-\sqrt{\frac12}\right)$
$f\left(-\sqrt{\frac12}\right)=\frac12\cdot\left(-\sqrt{\frac12}^4\right)-\frac32\cdot\left(-\sqrt{\frac12}^2\right)+2=1{,}375=\frac{11}8=1\frac38$
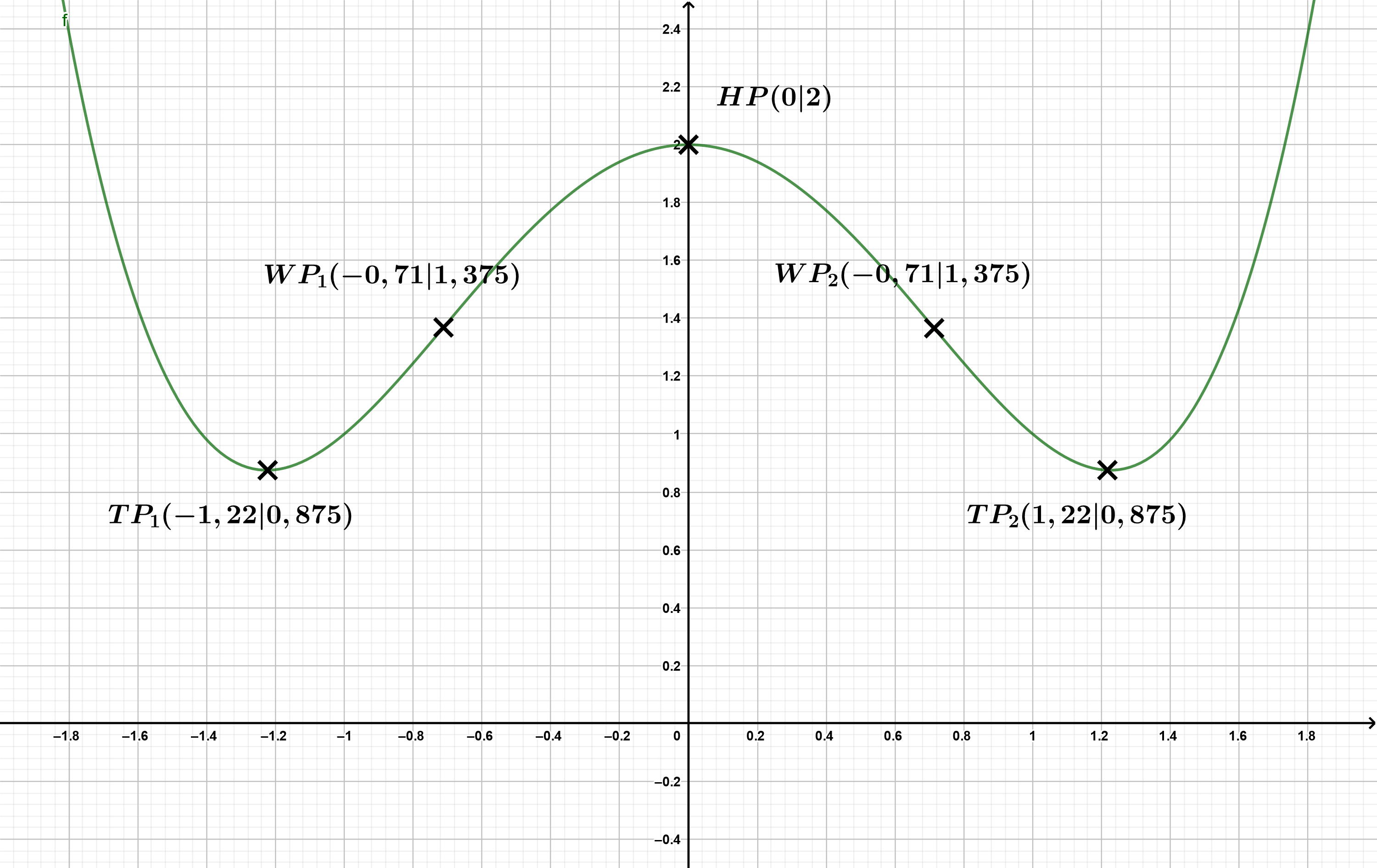
Ergebnis
${\mathrm{WP}}_1=\left(\sqrt{\frac12}\vert\frac{11}8\right)$
${\mathrm{WP}}_2=\left(-\sqrt{\frac12}\vert\frac{11}8\right)$
Grenzwertbetrachtung
$D_{f} = R D_f=ℝ$ . Da die Funktion keine Definitionslücken hat, muss nur das Grenzwertverhalten der Funktion für $x\rightarrow\pm\infty$ betrachtet werden.
gegen $+\infty$
$\lim_{x\rightarrow\infty}\frac12\overset{\rightarrow\infty}{\overset︷{x^4}}-\frac32\cdot\overset{\rightarrow\infty}{\overset︷{x^2}}+2=\infty$
gegen $-\infty$
$\lim_{x\rightarrow-\infty}\frac12\overset{\rightarrow\infty}{\overset︷{x^4}}-\frac32\cdot\overset{\rightarrow\infty}{\overset︷{x^2}}+2=\infty$
Symmetrie
Da alle Exponenten zur Basis $x$ gerade sind, ist der Graph der Funktion achsensymmetrisch.
Das Kriterium von y-Achsensymmetrie lautet:
$f\left(x\right)=f\left(-x\right)$
Durch Ersetzen von $x$ im rechten Funktionsterm mit $- x$ wird überprüft, ob die Funktion eine y-Achsensymmetrie aufweist.
$\frac12x^4-\frac32x^2+2\overset?=\frac12\left(-x\right)^4-\frac32\left(-x\right)^2+2$
$\frac12x^4-\frac32x^2+2=\frac12x^4-\frac32x^2+2$
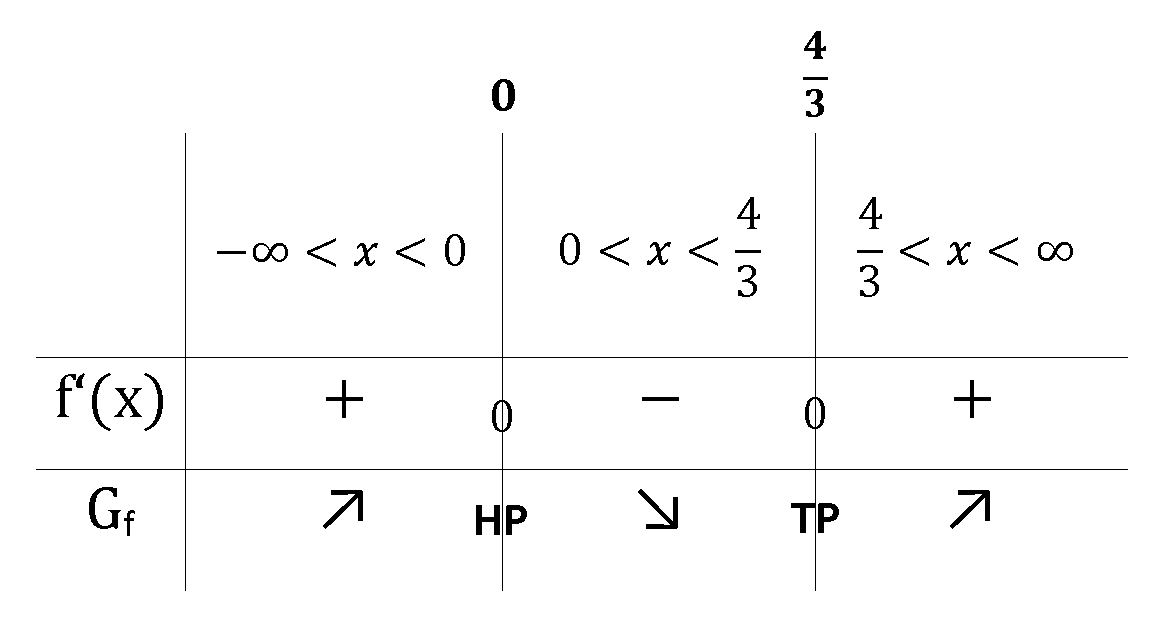
Monotonieverhalten
Die Monotonie wird mithilfe einer Tabelle bestimmt.
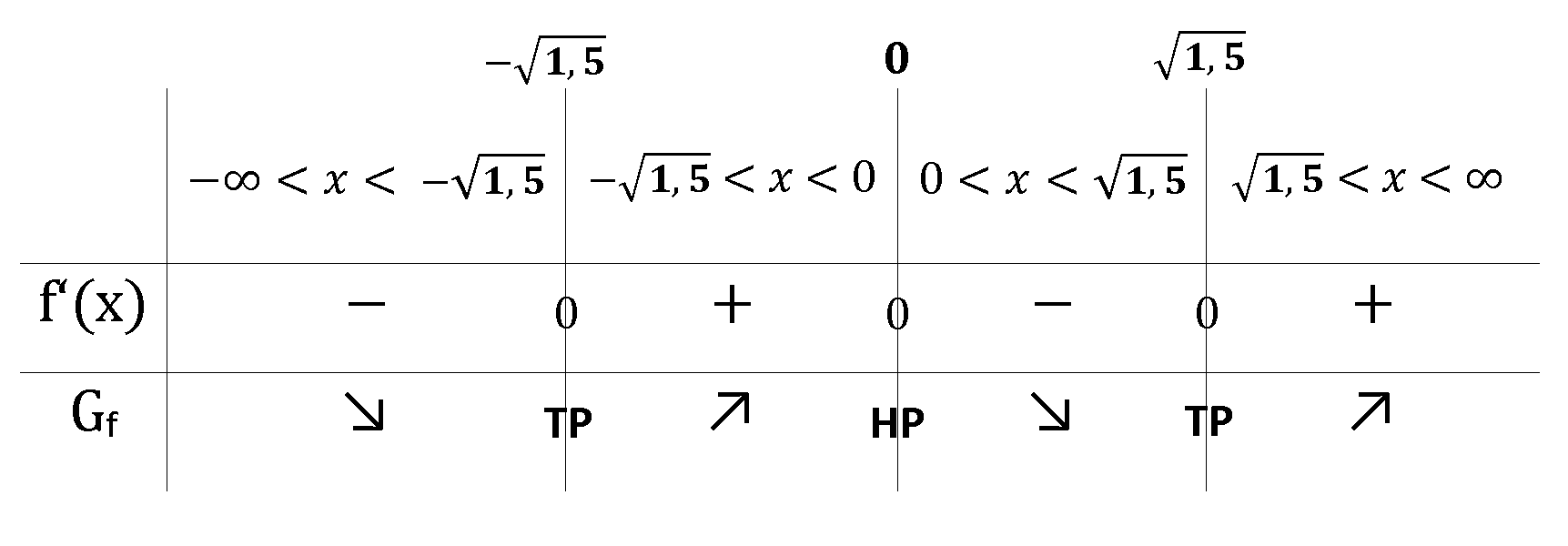
Graph
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Definitionsbereich festlegen

Polynomdivision

Symmetrieverhalten

Durch Betrachtung

Durch Berechnung

Ableitungen

Erste Ableitung

Zweite Ableitung

Extrema bestimmen