Aufgaben zu der Tangente

Hier findest du Aufgaben, in welchen du verschiedene Rechnungen rund um die Tangente üben kannst.

1
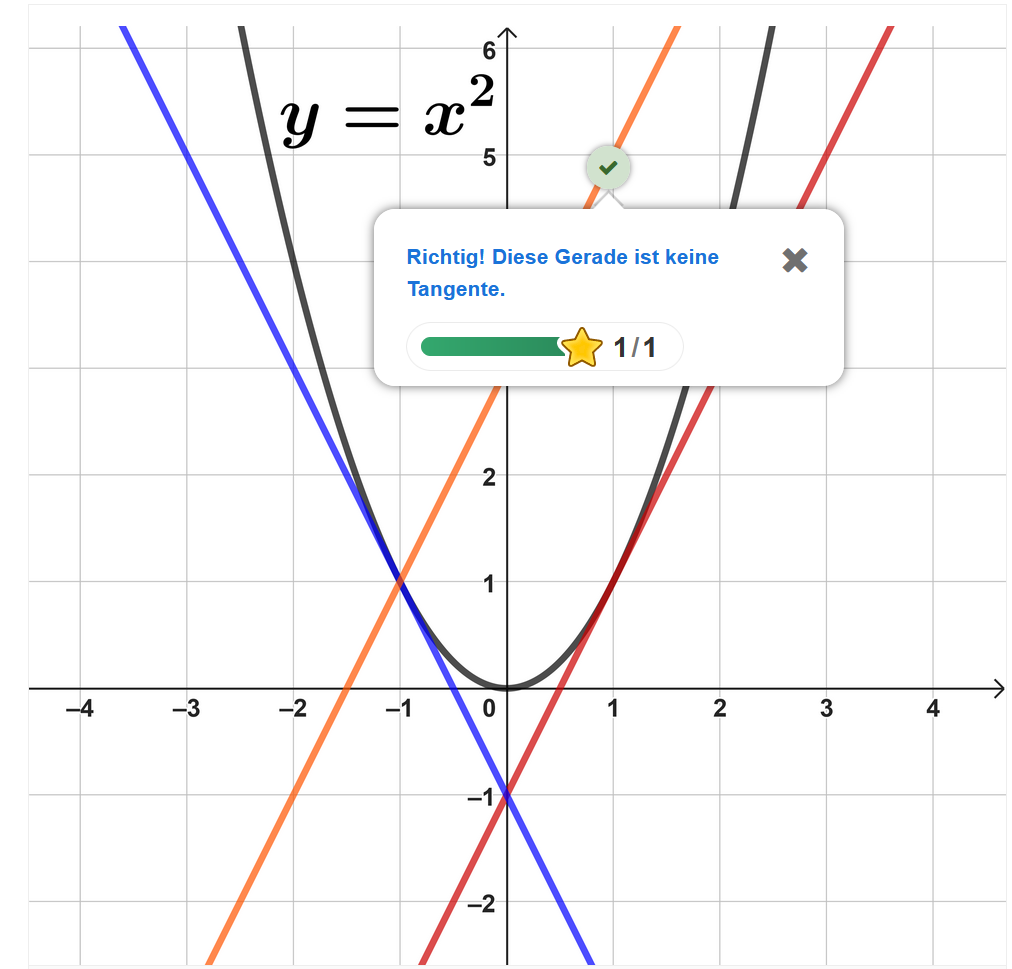
Finde die Gerade
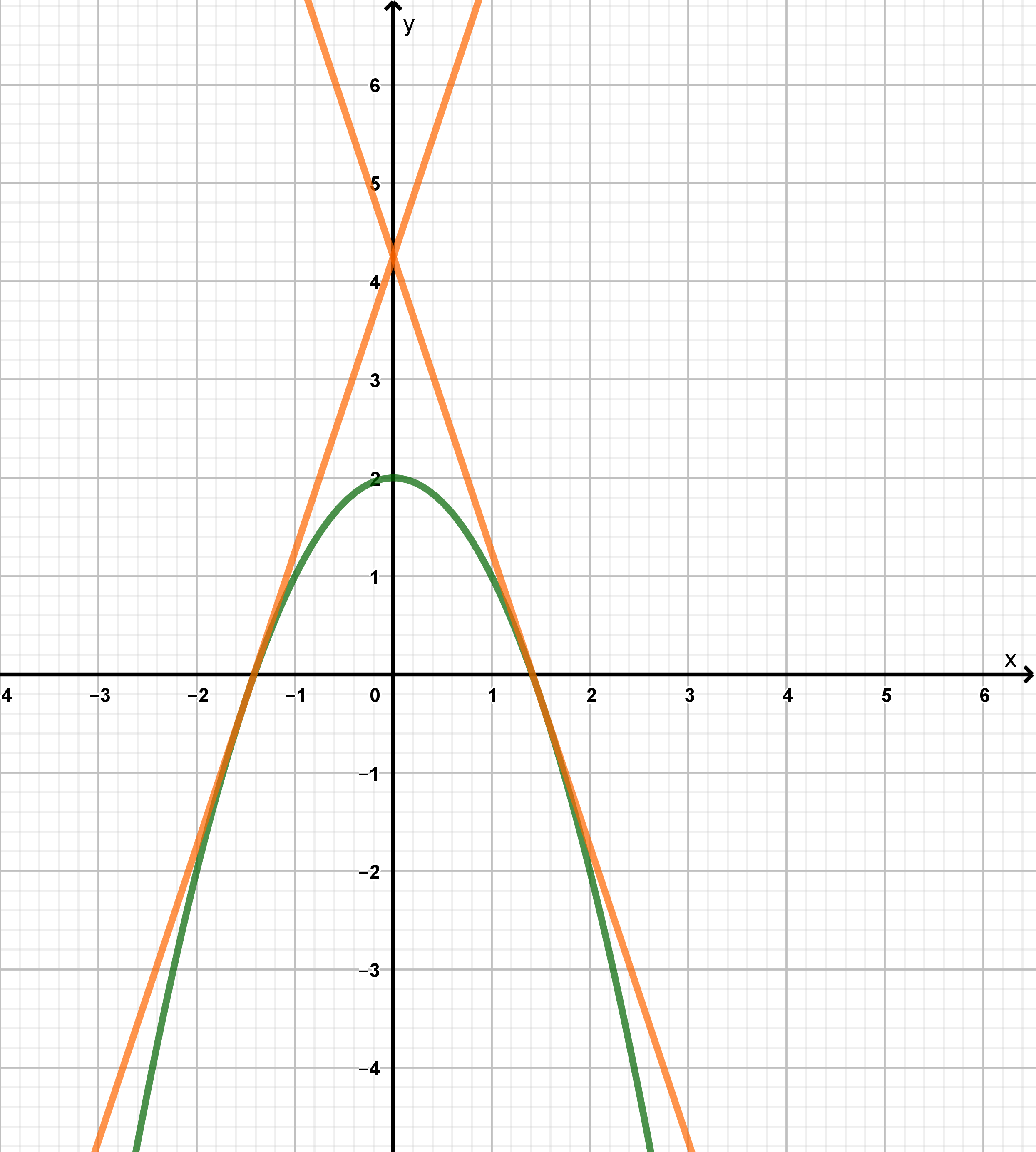
Welche dieser Geraden ist keine Tangente? Wähle aus.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Lösung
Lösung
Die orange Gerade ist keine Tangente.
Denn sie berührt den Graphen an keiner Stelle, sondern schneidet diesen.
Die anderen beiden Geraden berühren den Graphen der Parabel und sind damit Tangenten.
2
Gegeben ist die Funktion $f(x)=x^2$ .
Stelle die Gleichung der Tangente im Punkt $P(2|y)$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente aufstellen
Stelle die Tangentengleichung auf:
$y=mx+t$
Die Tangente hat im Punkt $P(2\mid y)$ die Steigung der Funktion $f(x)=x^2$ , diese bestimmt man mit Hilfe der Ableitung.
$f'(x)=2x$
Bestimmen der Steigung $m$ : $m=f^\prime(2)=4$
$y=f'(2)=4$
Der Punkt $P$ liegt auf $f(x)$ .
$\Rightarrow P(2\mid 4)$
$4=4\cdot2+t$
Bestimme den $y$ -Achsen Abschnitts durch einsetzen von $P$ in die Geradengleichung.
$\displaystyle 4$ $=$ $\displaystyle 8+t$ $\displaystyle -8$
$\displaystyle -4$ $=$ $\displaystyle t$
$\Rightarrow$ Die Tangente ist gegeben durch die Gleichung

Bestimme die Gleichung der Tangente an den Graphen der Funktion $f(x)=2x^2$ , wobei die Tangente parallel zur Geraden $g:2x+1-y=0$ verlaufen soll.

Bestimme die Gleichung der Tangente an die Funktion $f(x)=3\cdot x^2$ , die senkrecht zur Geraden $h:2\cdot y-3\cdot x+6=0$ ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentengleichung bestimmen

Die Gleichung einer Tangente ist eine Geradengleichung:

$y=mx+t$

Die Tangente soll senkrecht zur Geraden $h:2y-3x+6=0$ sein, stelle die Gleichung von $h$ nun so um, dass du die Steigung ablesen kannst:

$\displaystyle 2y-3x+6$	$=$	$\displaystyle 0$	$\displaystyle +3x$
$\displaystyle 2y + 6$	$=$	$\displaystyle 3x$	$\displaystyle -6$
$\displaystyle 2y$	$=$	$\displaystyle 3x - 6$	$\displaystyle :2$
$\displaystyle y$	$=$	$\displaystyle \frac{3}{2}x-3$

Die Steigung der Gerade $h$ ist $m_h=\frac32$ .

Die Tangente soll senkrecht zur Geraden $h$ sein.

$\displaystyle \Rightarrow m\cdot m_h$	$=$	$\displaystyle -1$	$\displaystyle :m_h$
$\displaystyle m$	$=$	$\displaystyle -\dfrac{1}{m_h}$
$\displaystyle m$	$=$	$\displaystyle -\dfrac{1}{\left(\frac32\right)}$
$\displaystyle m$	$=$	$\displaystyle -\dfrac23$

Darüber hinaus muss im Berührpunkt der Tangente und der Funktion $f$ die Steigung von $f$ gleich $-\frac23$ sein.

$f^\prime(x)=6x$

Damit berechnen wir die $x$ -Koordinate des Berührpunktes $P(x\mid y)$ .

$f^\prime(x)=6x\stackrel{!}{=}-\dfrac23$

$\Rightarrow x=-\dfrac19$

Außerdem liegt $P(-\dfrac19\mid y)$ auf $f$ .

$f(-\dfrac19)=3\cdot\left(-\dfrac19\right)^2=\dfrac1{27}$

Also ist $P(-\dfrac19\mid\dfrac1{27})$ .

Bestimmen des $y$ -Achsen Abschnitts durch einsetzen von $P$ in die Geradengleichung:

$\displaystyle \dfrac{1}{27}$	$=$	$\displaystyle -\dfrac23\cdot(-\dfrac19)+t$
$\displaystyle -\dfrac{1}{27}$	$=$	$\displaystyle \dfrac2{27}+t$	$\displaystyle -\dfrac{2}{27}$
$\displaystyle -\dfrac{1}{27}$	$=$	$\displaystyle t$

$\Rightarrow$ Die Tangente ist gegeben durch die Gleichung

\displaystyle y=-\frac23x-\frac1{27}

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Bestimme die Tangenten an die Funktion $f(x)=-x^2+2$ , die sich im Punkt $P(0\mid4{,}25)$ schneiden.

Bestimme die Gleichung der Tangente an die Funktion $f(x)=\sqrt{x}-2$ durch den Punkt $P(x\mid0)$ .

An die Funktion $f(x)=-0{,}2\cdot(x-2)^2-2{,}5$ soll vom Punkt $P(0\mid3)$ aus eine Tangente mit negativer Steigung gelegt werden. Bestimme die Gleichung der Tangente und den Berührpunkt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden

Stelle die Tangentengleichung auf. Sie hat die allgemeine Form:

$y=mx+t$

Der Punkt $P(0\mid3)$ liegt auf der Tangente. Setze seine Koordinaten in die Geradengleichung ein.

$\displaystyle 3$	$=$	$\displaystyle m\cdot0+t$
$\displaystyle 3$	$=$	$\displaystyle t$

Wir errechnen die Schnittpunkte der Geraden mit dem Graphen der Funktion $f:$

$\displaystyle mx+t$	$=$	$\displaystyle f\left(x\right)$
	↓	Setze $t=3$ und $f(x)=-0{,}2\cdot(x-2)^2-2{,}5$ ein.
$\displaystyle mx+3$	$=$	$\displaystyle -0{,}2\cdot(x-2)^2-2{,}5$
	↓	2. binomische Formel anwenden.
$\displaystyle mx+t$	$=$	$\displaystyle -0{,}2\cdot\left(x^2-4x+4\right)-2{,}5$
	↓	Klammer auflösen.
$\displaystyle mx+3$	$=$	$\displaystyle -0{,}2x^2+0{,}8x-0{,}8-2{,}5$
$\displaystyle mx+3$	$=$	$\displaystyle -0{,}2x^2+0{,}8x-3{,}3$	$\displaystyle -3$
$\displaystyle mx$	$=$	$\displaystyle -0{,}2x^2+0{,}8x-6{,}3$	$\displaystyle -mx$
$\displaystyle 0$	$=$	$\displaystyle -0{,}2x^2+0{,}8x-6{,}3-mx$
	↓	Umsortieren und einklammern.
$\displaystyle 0$	$=$	$\displaystyle -0{,}2x^2+\left(0{,}8-m\right)x-6{,}3$	$\displaystyle \cdot\left(-5\right)$
	↓	$\cdot\left(-5\right)$ ist das Gleiche wie $:(-0{,}2)$ .
$\displaystyle 0$	$=$	$\displaystyle x^2-\left(4-5m\right)x+31{,}5$
	↓	Mitternachtsformel anwenden.
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle \frac{(4-5m)\pm\sqrt{\left(-(4-5m)\right)^2-4\cdot1\cdot31{,}5}}{2\cdot1}$
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle \frac{(4-5m)\pm\sqrt{(4-5m)^2-126}}{2}$

Für Tangente muss gelten, dass sie nur einen Berührpunkt mit dem Graphen der Funktion $f$ besitzen. Daher darf es nur eine Lösung der Mitternachtsformel geben.

Um nur eine Lösung für die Gleichung

\displaystyle y=-\frac23x-\frac1{27}

zu erhalten muss die Diskriminante $D=(4-5m)^2-126$ gleich 0 sein.

$\displaystyle D=\left(4-5m\right)^2-126$	$=$	$\displaystyle 0$	$\displaystyle +126$
$\displaystyle \left(4-5m\right)^2$	$=$	$\displaystyle 126$	$\displaystyle \sqrt{ }$
$\displaystyle 4-5m$	$=$	$\displaystyle \pm\sqrt{126}$	$\displaystyle -4$
$\displaystyle -5m$	$=$	$\displaystyle \pm\sqrt{126}-4$	$\displaystyle :\left(-5\right)$
$\displaystyle m$	$=$	$\displaystyle \mp\frac{\sqrt{126}}{5}+\frac{4}{5}$
$\displaystyle m$	$=$	$\displaystyle \mp\frac{3\sqrt{14}}{5}+\frac{4}{5}$
$\displaystyle m$	$=$	$\displaystyle \mp\frac{3}{5}\sqrt{14}+\frac{4}{5}$

$m_1=+\frac35\sqrt{14}+\frac45\approx3{,}04$

$m_2=-\frac{3}{5}\sqrt{14}+\frac{4}{5}\approx-1{,}44$

$\Rightarrow$ Da die Tangente negative Steigung haben soll, ist sie gegeben durch die Gleichung

\displaystyle y=-\frac23x-\frac1{27}

Zusatz: Darstellung des Graphen und der gesuchten Tangente im Koordinatensystem

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

8
Gegeben ist die Funktion $f(x)=2x^3+x^2-0{,}5x+2$ .
Bestimme die Gleichung der Tangente an der Stelle $x=7$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an einen Graphen
Da die Tangente eine Gerade ist, machst du für sie den Ansatz für eine lineare Funktion, nämlich $y=mx+t$ .
Ansatz: $y=mx+t$
In diesem Ansatz musst du $m$ und $t$ bestimmen.
Zuerst berechnest du $m$ :
$m$ ist die Steigung der Tangente.
Die Tangente hat an der Stelle x=7 die Steigung der Funktion $f(x)=2x^3+x^2-0{,}5x+2$ ,
und diese Steigung bestimmt man mit Hilfe der Ableitung von $f$ .
Bilde daher die Ableitung $f'(x)$ .
$f'(x)=6x^2+2x-0{,}5$
Setze $x=7$ in diese Ableitung ein und berechne so die Steigung $m$ der Tangente.
$m=f'(7)=307{,}5$
Dieses $m$ kannst du nun in den Ansatz $y=mx+t$ einsetzen und erhältst:
$y=307{,}5x+t$
Nun musst du noch $t$ bestimmen.
Dazu brauchst du einen Punkt, der auf der Geraden liegt, und den du in den Ansatz einsetzen kannst.
Dafür kommt natürlich nur der Punkt $P$ bei $x=7$ in Frage, an dem die Tangente den Graphen von $f$ berührt.
$P(7|y_P)$
Da $P$ auf dem Graphen von $f$ liegt, erhältst du den $y$ -Wert von $P$ dadurch, dass du
$x=7$ in $f(x)$ einsetzt.
$y_P=f(7)=733{,}5$
Der Punkt $P$ hat also die Koordinaten:
$P(7|733{,}5)$
Setze $P$ in die Geradengleichung $y=307{,}5x+t$ ein.
$733{,}5=307{,}5\cdot7+t$
Löse diese Gleichung nach $t$ auf, um den $y$ -Achsenabschnitt $t$ der Tangente zu berechnen.
$733{,}5=2152{,}5+t\quad |-2152{,}5$
$-1419=t$
Dies setzt du in den Ansatz für die Tangente ein, wobei du nun wieder $x$ und $y$ (und nicht mehr die Koordinaten von $P$ ) schreibst.
Damit erhältst du die gesuchte Tangentengleichung.
$\Rightarrow$ Die Tangentengleichung ist gegeben durch die Gleichung:
$y=307{,}5x-1419$

Tangente bestimmen zu gegebener Funktion und Stelle

Stelle die Funktionsgleichung $g\left(x\right)$ der Tangente auf, die die jeweilge Funktion $f\left(x\right)$ in der angegebenen Stelle berührt.

$f\left(x\right)=-3x^2+2x,~x_0=2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentenformel

Schritt	Beispiel
Berechne $f(x_0)$ .	$f(2)=(-3)\cdot 2^2+2\cdot 2=-12+4=-8$
Bestimme $f'(x)$ .	$f'(x)=-6x+2$
Berechne $f'(x_0)$ .	$f'(2)=(-6)\cdot 2+2=-10$
Setze $x_0,f(x_0),f'(x_0)$ in die Formel ein.	$g(x)=f'(x_0)(x-x_0)+f(x_0)$ $\phantom{g(x)}=-10(x-2)-8$
Vereinfache.	$g(x)=-10x+12$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$f(x)=\dfrac{2}{3}x^3-2,~x_0=-1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentenformel

Schritt	Beispiel
Berechne $f(x_0)$ .	$f(-1)=\dfrac{2}{3}\cdot(-1)^3-2=-\dfrac{2}{3}-2=-\dfrac{8}{3}$
Bestimme $f'(x)$ .	$f'(x)=2x^2$
Berechne $f'(x_0)$ .	$f'(-1)=2\cdot(-1)^2=2$
Setze $x_0,f(x_0),f'(x_0)$ in die Formel ein.	$g(x)=f'(x_0)(x-x_0)+f(x_0)$ $\phantom{g(x)}=2(x+1)-\dfrac{8}{3}$
Vereinfache.	$g(x)=2x-\dfrac{2}{3}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$f(x)=\dfrac{1}{8}x^4-3x^2+x,~x_0=2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentenformel

Schritt	Beispiel
Berechne $f(x_0)$ .	$f(2)=\dfrac{1}{8}\cdot 2^4-3\cdot 2^2+2$ $\\$ $\phantom{f(x_0)}=2-12+2=-8$
Bestimme $f'(x)$ .	$f'(x)=\dfrac{1}{2}x^3-6x+1$
Berechne $f'(x_0)$ .	$f'(2)=\dfrac{1}{2}\cdot 2^3-6\cdot 2+1$ $\\$ $\phantom{f'(2)}=4-12+1=-7$
Setze $x_0,f(x_0),f'(x_0)$ in die Formel ein.	$g(x)=f'(x_0)(x-x_0)+f(x_0)$ $\\$ $\phantom{g(x)}=-7(x-2)-8$
Vereinfache.	$g(x)=-7x+6$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Tangente bestimmen zu gegebener Funktion und Steigung

Bestimme den Funktionsterm der Tangente, die die Funktion $f$ mit der angegebenen Steigung $m$ berührt. Falls es mehrere Möglichkeiten gibt, bestimme alle Tangentengleichungen.

$f(x)=-\dfrac{1}{2}x^2+3x,~m=-2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph

Allgemein	Beispiel
Berechne $f'(x)$	$f'(x)=-x+3$
Setze mit der Steigung $m$ gleich.	$-2=-x+3$
Löse nach $x$ bzw. $x_0$ auf.	$x_0=5$
Berechne $f(x_0)$	$f(5)=-\dfrac{25}{2}+15=\dfrac{5}{2}$
Setze $x_0,f(x_0),m$ in die Tangentenformel ein.	$g(x)=f'(x_0)(x-x_0)+f(x_0)$ $\\$ $\phantom{g(x)}=-2(x-5)+\dfrac{5}{2}$
Vereinfache.	$-2x+ \dfrac{25}{2}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$f(x)=-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+11x-6,~m=5$

Allgemein	Beispiel
Berechne $f'(x)$	$f'(x)=-x^2+x+11$
Setze mit der Steigung $m$ gleich.	$5=-x^2+x+11$
Zwischenschritt: Bringe in die Nullform $\\$ und bestimme $p,q$ .	$0=x^2-x-6$
Löse nach $x$ bzw. $x_0$ auf.	$x_{1/2}=-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}$ $\\$ Setze in die Formel $\\$ $p=-1,~q=-6$ ein: $\\$ $x_{1/2}=-\dfrac{(-1)}{2}\pm\sqrt{\left(\dfrac{(-1)}{2}\right)^2+6}$ $\\$ $\phantom{x_{1/2}} =\dfrac{1}{2}\pm\sqrt{\dfrac{1}{4}+\dfrac{24}{4}}$ $\\$ $\phantom{x_{1/2}}=\dfrac{1}{2}\pm\sqrt{\dfrac{25}{4}}$ $\\$ $\phantom{x_{1/2}}=\dfrac{1}{2}\pm\dfrac{5}{2}$ $\\$ $x_1=3$ $\\$ $x_2=-2$

Hier ergeben sich zwei Möglichkeiten. Die Funktion $f(x)$ besitzt an zwei Stellen die vorgegebene Steigung und damit ist es möglich zwei Tangenten anzulegen.

Allgemein	Beispiel
Berechne $f(x_1),f(x_2)$	$f(3)=-\dfrac{1}{3}\cdot 3^3+\dfrac{1}{2}\cdot 3^2+11\cdot 3-6$ $\\$ $\phantom{f(3)}=-9+\dfrac{9}{2}+33-6=\dfrac{45}{2}$ $\\$ $f(-2)=-\dfrac{1}{3}\cdot (-2)^3+\dfrac{1}{2}\cdot (-2)^2+11\cdot (-2)-6$ $\\$ $\phantom{f(-2)}=\dfrac{8}{3}+2-22-6=-\dfrac{70}{3}$
Setze $x_1,f(x_1),m$ in die $\\$ Tangentenformel ein.	$g_1(x)=f'(x_0)(x-x_0)+f(x_0)$ $\\$ $\phantom{g(x)}=5(x-3)+\dfrac{45}{2}$
Setze $x_2,f(x_2),m$ in die $\\$ Tangentenformel ein.	$g_2(x)=f'(x_0)(x-x_0)+f(x_0)$ $\\$ $\phantom{g(x)}=5(x+2)-\dfrac{70}{3}$
Vereinfache.	$g_1(x)=5x+\dfrac{15}{2}$ $g_2(x)=5x-\dfrac{40}{3}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle m_{1{,}2}x+4{,}25$	$=$	$\displaystyle -x^2+2$	$\displaystyle -m_{1{,}2}x$
$\displaystyle 4{,}25$	$=$	$\displaystyle -x^2+2-m_{1{,}2}x$	$\displaystyle -4{,}25$
$\displaystyle 0$	$=$	$\displaystyle -x^2-m_{1{,}2}x-2{,}25$

$\displaystyle m_{1{,}2}^2-9$	$=$	$\displaystyle 0$	$\displaystyle +9$
$\displaystyle m_{1{,}2}^2$	$=$	$\displaystyle 9$	$\displaystyle \sqrt{}$
$\displaystyle m_{1{,}2}$	$=$	$\displaystyle \pm 3$

$\displaystyle f(x)$	$=$	$\displaystyle \sqrt{x} -2$
$\displaystyle \Rightarrow0$	$=$	$\displaystyle \sqrt{x} -2$	$\displaystyle +2$
$\displaystyle 2$	$=$	$\displaystyle \sqrt{x}$	$\displaystyle ^2$
$\displaystyle 4$	$=$	$\displaystyle x$

$\displaystyle 4$	$=$	$\displaystyle 8+t$	$\displaystyle -8$
$\displaystyle -4$	$=$	$\displaystyle t$

$\displaystyle 2x + 1 - y$	$=$	$\displaystyle 0$	$\displaystyle +y$
$\displaystyle 2x + 1$	$=$	$\displaystyle y$

$\displaystyle \frac{1}{2}$	$=$	$\displaystyle 2\cdot \dfrac12 + t$
$\displaystyle \dfrac12$	$=$	$\displaystyle 1 + t$	$\displaystyle -1$
$\displaystyle -\dfrac12$	$=$	$\displaystyle t$

$\displaystyle 0$	$=$	$\displaystyle \dfrac14 \cdot 4 + t$
$\displaystyle 0$	$=$	$\displaystyle 1 + t$	$\displaystyle -1$
$\displaystyle -1$	$=$	$\displaystyle t$

Aufgaben zu der Tangente

Finde die Gerade

Lösung

Zusatz: Darstellung des Graphen und der gesuchten Tangente im Koordinatensystem

Tangente bestimmen zu gegebener Funktion und Stelle

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Tangente bestimmen zu gegebener Funktion und Steigung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?