Aufgaben zur Flächenberechnung am Dreieck
Übe hier mit verschiedenen Aufgaben die Flächenberechnung von Dreiecken.
- 1
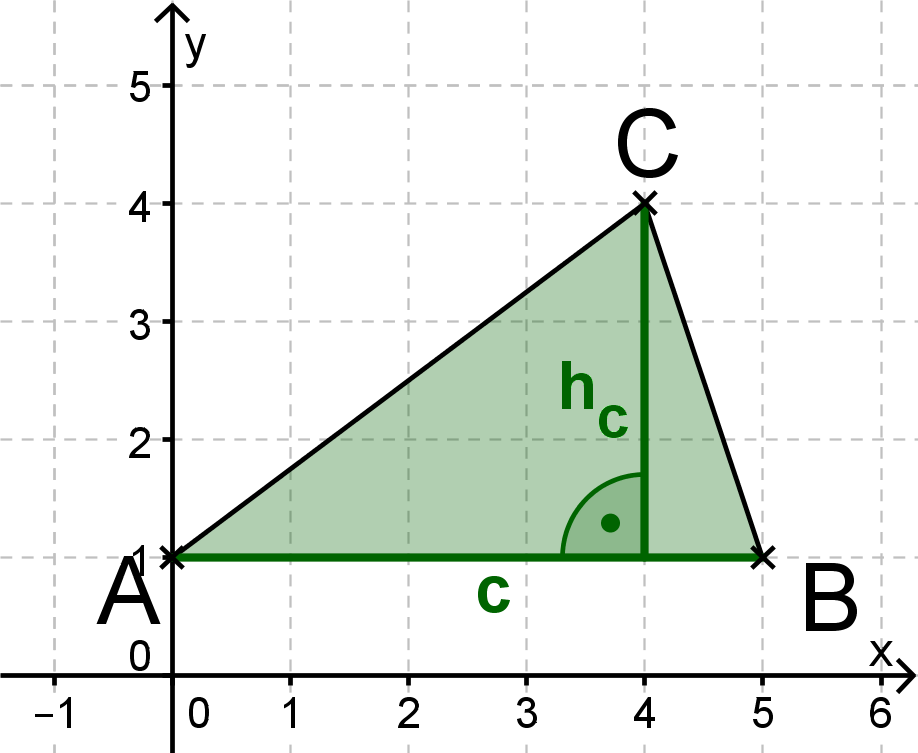
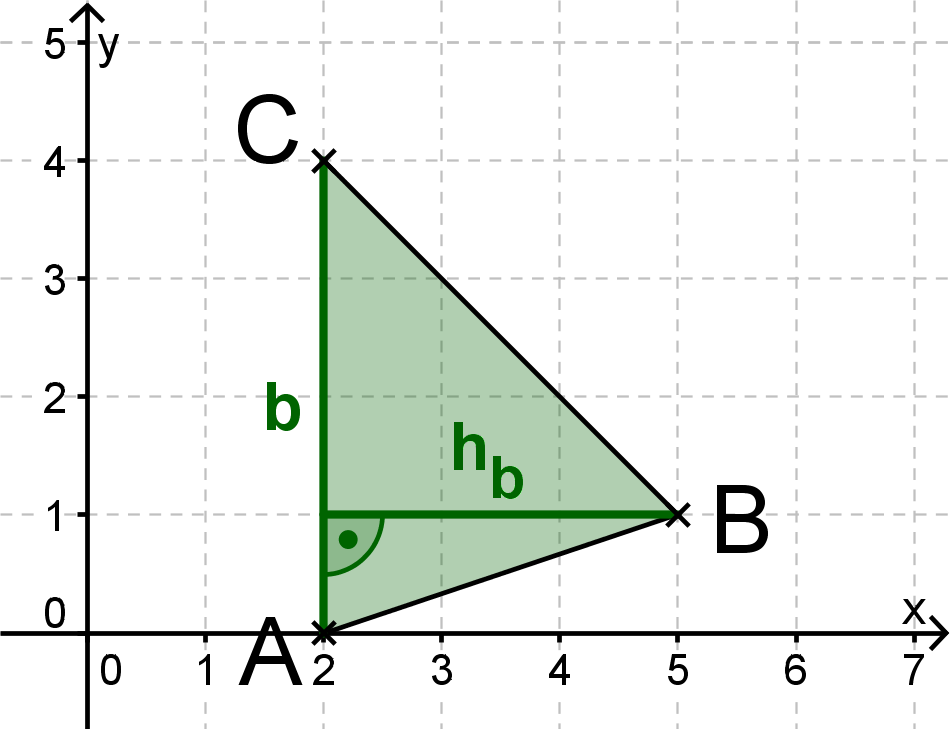
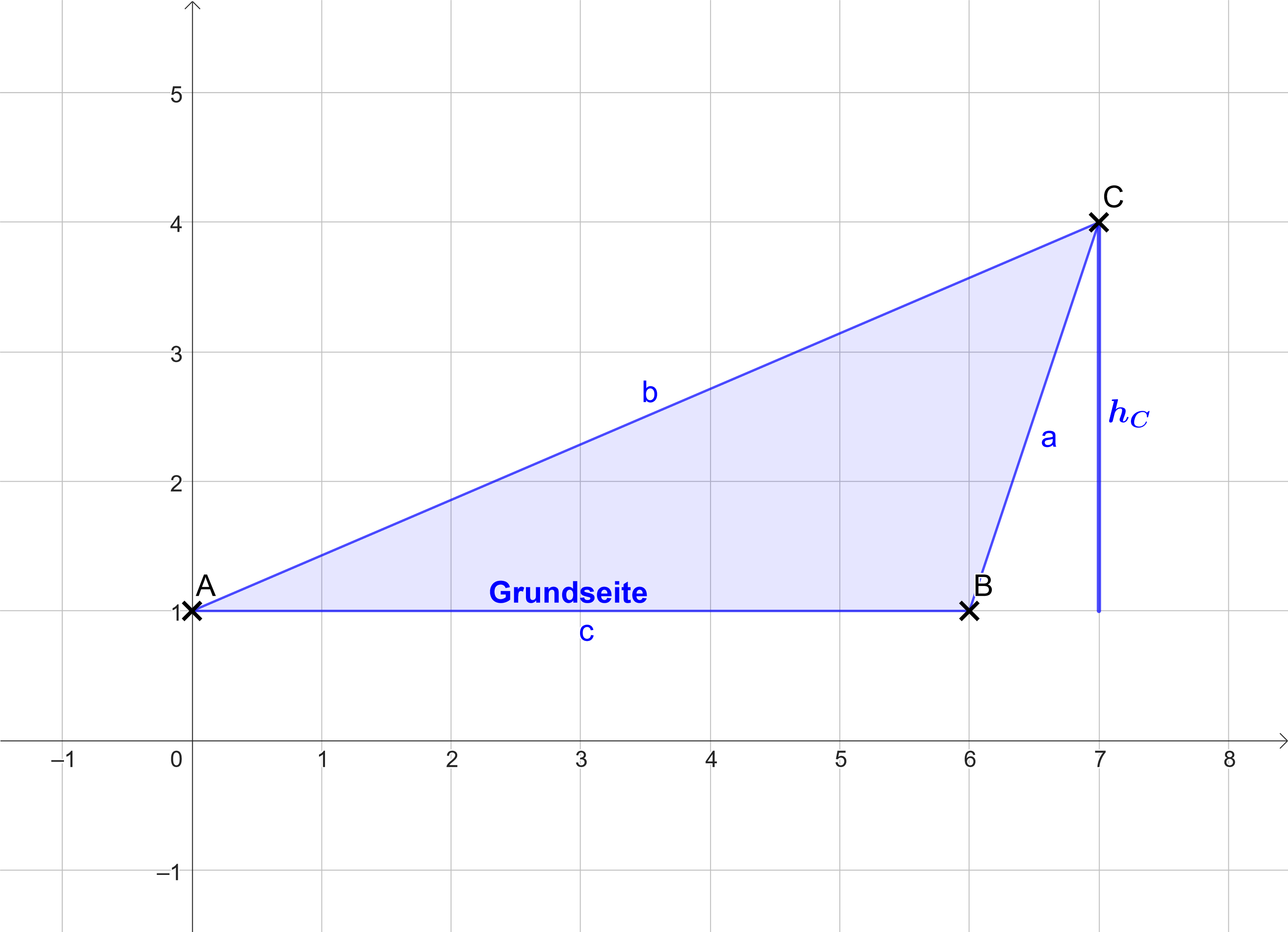
Berechne den Flächeninhalt folgender Dreiecke.
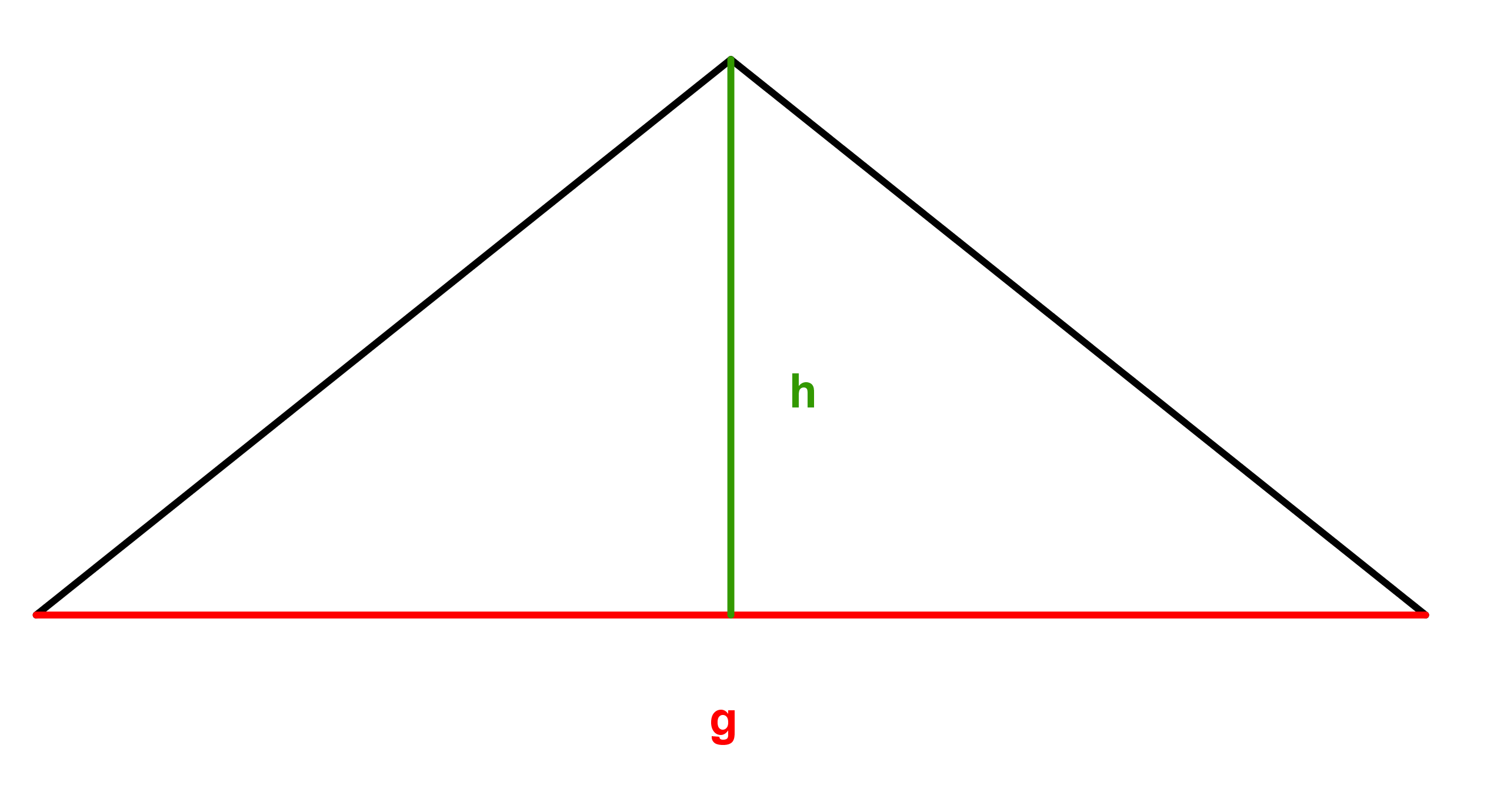
Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²
- 2
Berechne das Gesuchte im gegebenen Dreieck.
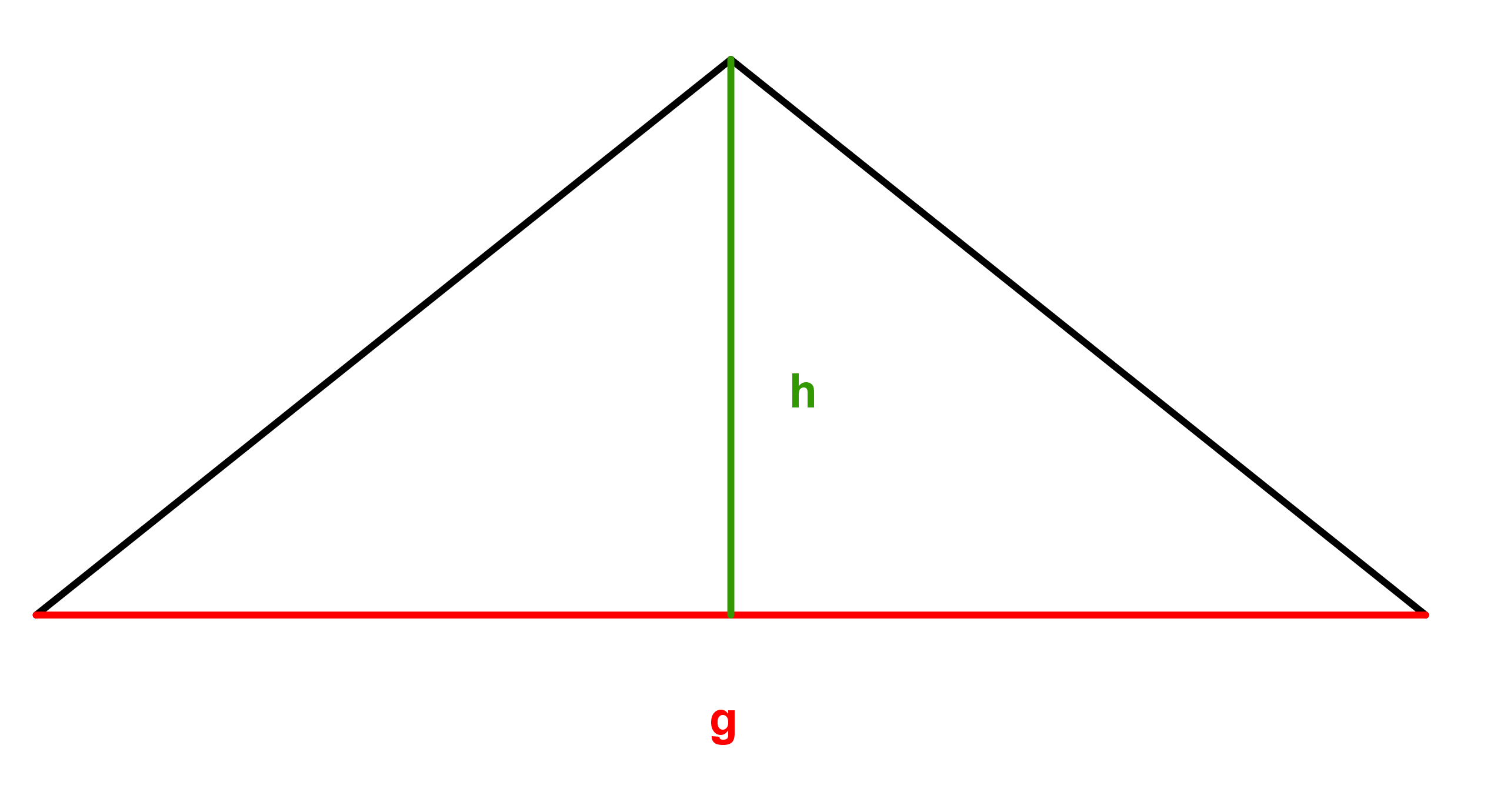
Gegeben ist die Höhe und der Flächeninhalt . Berechne die Grundseite .
cmGegeben ist die Grundlinie und der Flächeninhalt . Berechne die Höhe .
cmGegeben ist der Flächeninhalt und die Grundlinie . Berechne die Höhe .
cmGegeben ist der Flächeninhalt und die Höhe . Berechne die Grundseite .
cmGegeben ist die Höhe und die Grundseite . Berechne den Flächeninhalt .
dm²Gegeben ist die Höhe und die Grundseite . Berechne den Flächeninhalt .
cm²
- 3
Berechne den Flächeninhalt folgender Dreiecke.
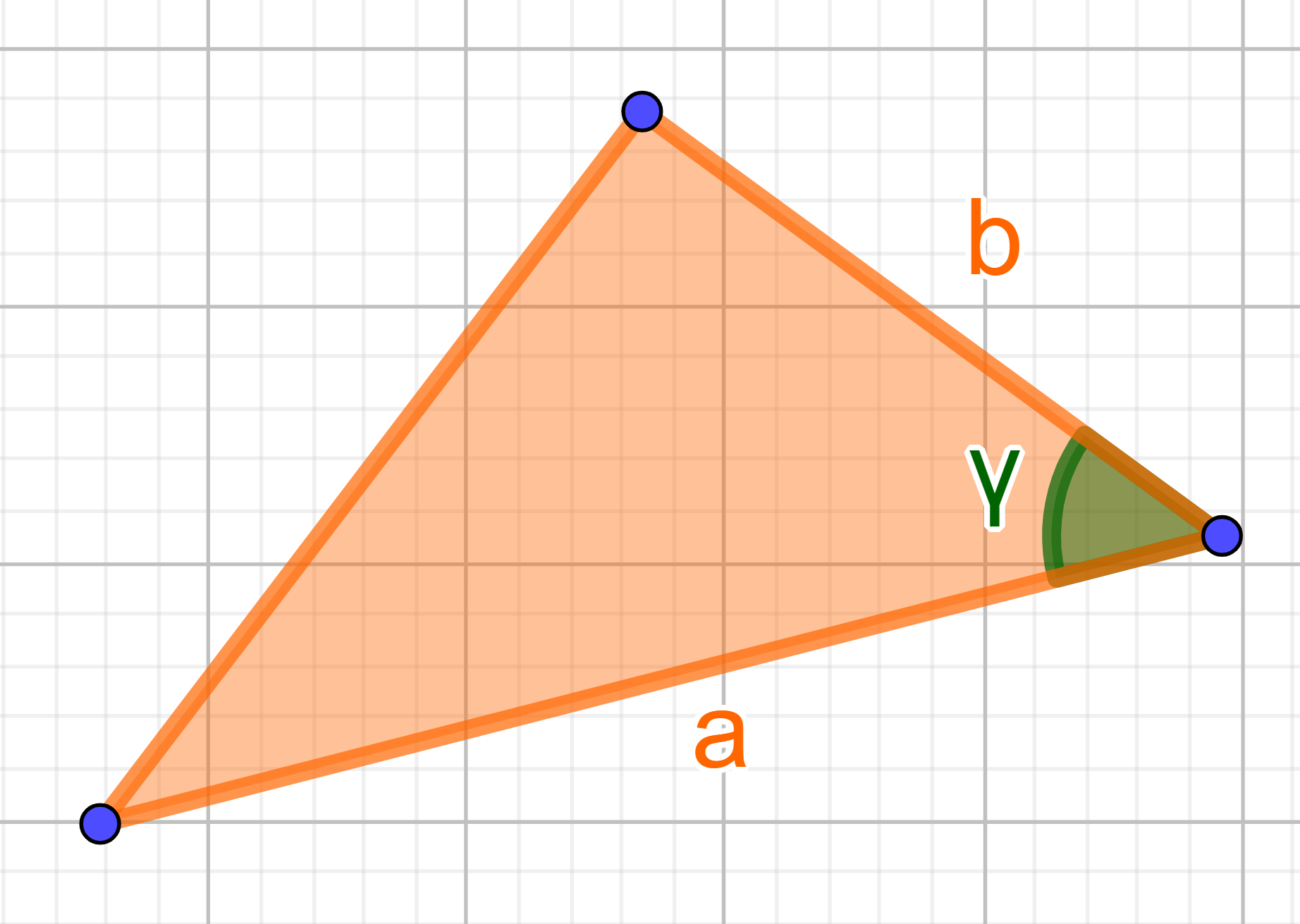
- cm²
- cm²
- cm²
- cm²
- 4
Berechne den Flächeninhalt des Dreiecks , wenn die Punkte , und folgendermaßen gegeben sind:
- Flächeneinheiten
- Flächeneinheiten
- cm²
- 5
Berechne den Flächeninhalt des Dreiecks , wenn die Punkte , und folgendermaßen gegeben sind:
- 6
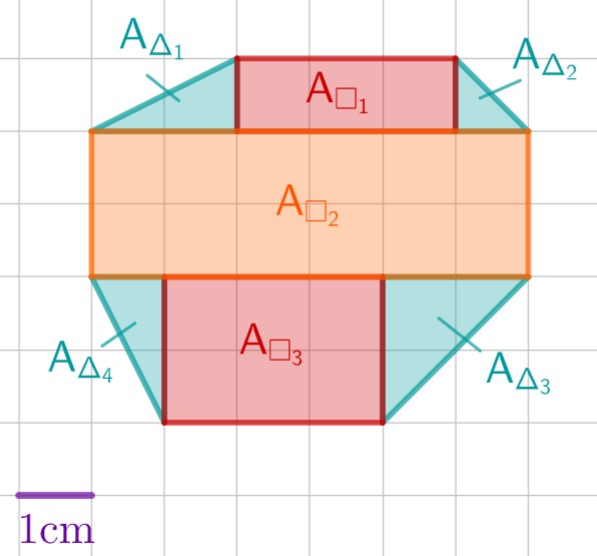
Berechne den Flächeninhalt des grünen Achtecks ABCDEFGH.
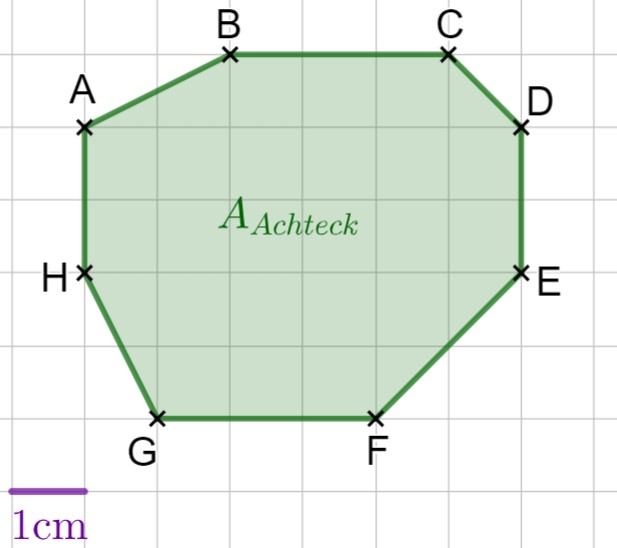 cm²
cm² - 7
Extremwertaufgaben der Flächenberechnung von Dreiecken
In den folgenden Aufgaben werden verschiedene Dreiecke beobachtet. Ziel der gesamten Aufgabe ist es, dasjenige Dreieck zu finden, das die maximale ( = größtmögliche ) Fläche hat.
Zeichne das gleichschenklige Dreieck mit und Höhe in ein Koordinatensystem ein.
Nun sollen Dreiecke aus dem Dreieck entstehen, indem die Grundseite von beiden Seiten um verkürzt werden und die Höhe um verlängert wird.
Zeichne die Dreiecke für , und in dasselbe Koordinatensystem wie das Dreieck ein.
Für welchen Wert von hat das Dreieck die maximale Fläche?
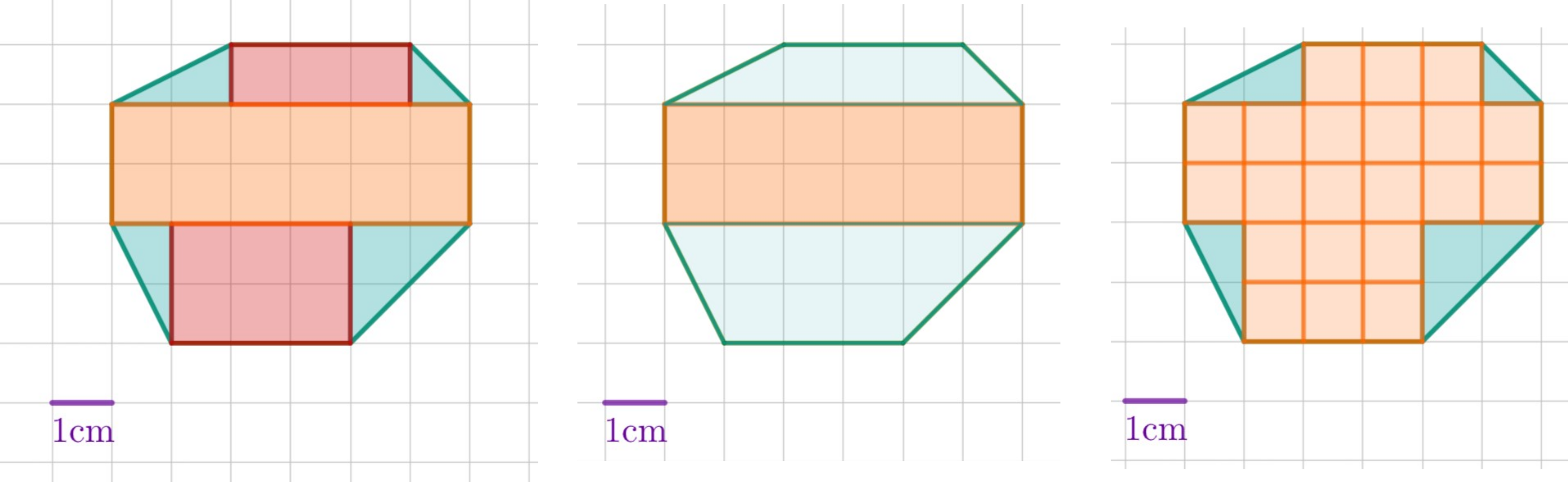
- 8
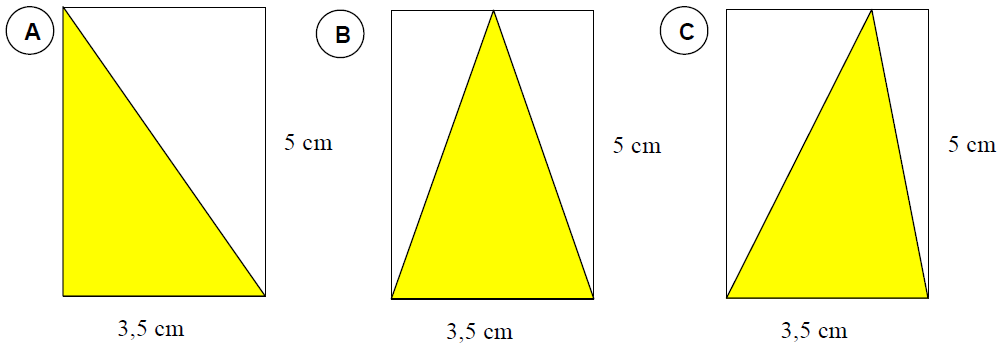
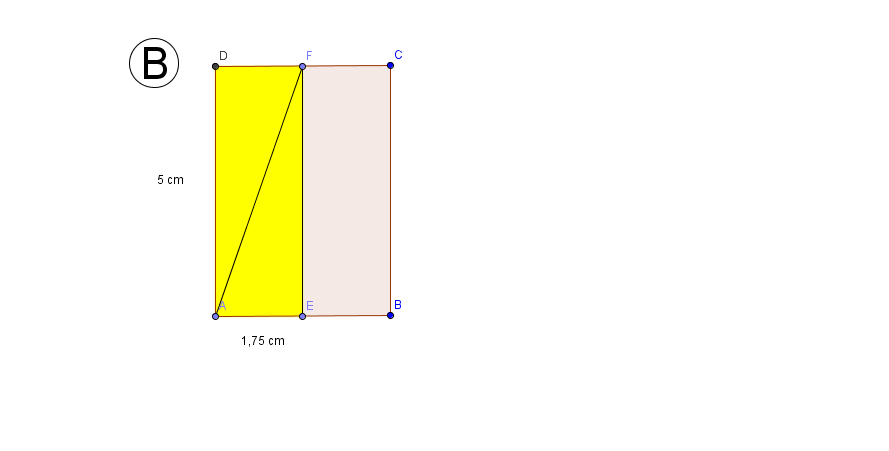
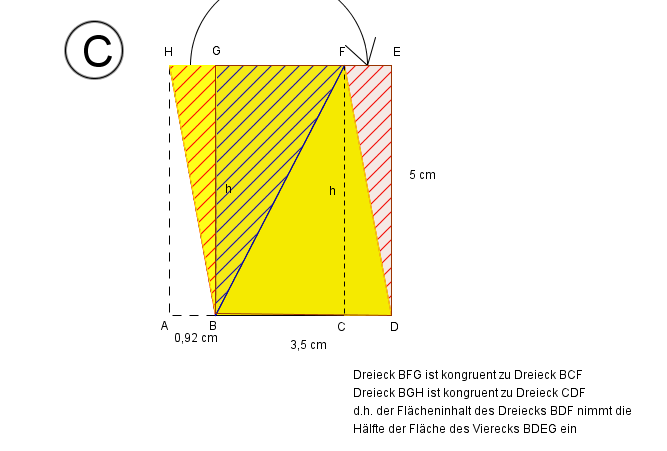
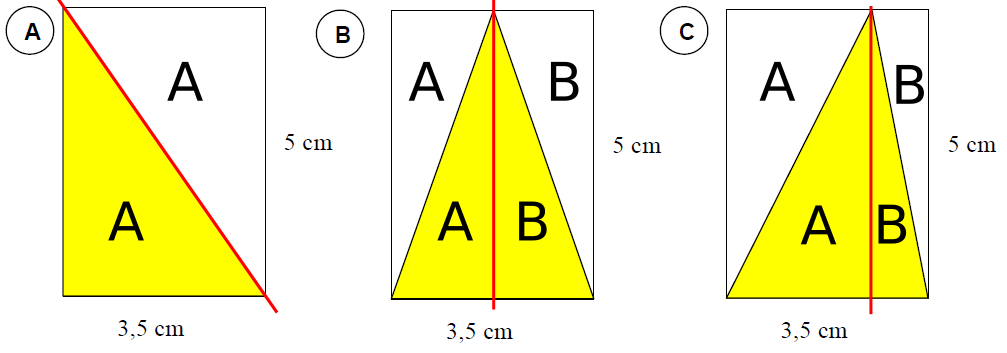
In Bild A sieht man sofort, dass der Flächeninhalt des gelben Dreiecks halb so groß ist wie der des umgebenden Rechtecks. Gilt dies auch für die Bilder B und C? Begründe deine Antwort mit Hilfe geeigneter Skizzen.
- 9
Trage die Punkte und in ein Koordinatensystem (1 LE = 1 cm) ein.
a) Gib 3 Möglichkeiten für die Koordinaten des Punktes an, so dass das Dreieck einen Flächeninhalt von hat.
b) Gib auch die Koordinaten eines Punktes an, so dass das Dreieck einen doppelt so großen Flächeninhalt wie das Dreieck hat.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?