Analysis, Teil A, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Gegeben ist die Funktion mit maximalem Definitionsbereich .
Geben Sie an. (1 BE)
Bestimmen Sie die Nullstellen von . (2 BE)
- 2
Gegeben sind die in definierten Funktionen f, g und h mit , und .
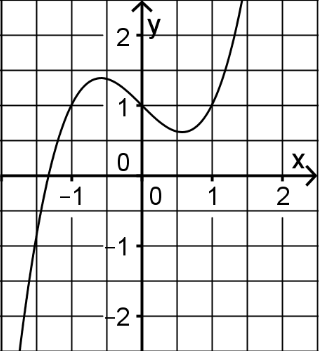
Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt. (3 BE)
Die erste Ableitungsfunktion von ist .Bestimmen Sie den Wert von . (2 BE)
- 3
Löse die Aufgabe.
Geben Sie einen positiven Wert für den Parameter a an, sodass die in definierte Funtion eine Nullstelle in hat. (1 BE)
Ermitteln Sie den Wert des Parameters , sodass die Funktion den maximalen Definitionsbereich besitzt. (2 BE)
Erläutern Sie, dass die in definierte Funktion den Wertebereich besitzt. (2 BE)
- 4
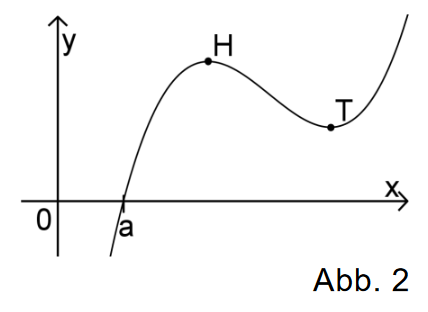
Abbildung 2 zeigt den Graphen einer in definierten differenzierbaren Funktion . Mithilfe des Newton-Verfahrens soll ein Näherungswert für die Nullstelle a von g ermittelt werden. Begründen Sie, dass weder die x-Koordinate des Hochpunkts H noch die x-Koordinate des Tiefpunkts T als Startwert des Newton-Verfahrens gewählt werden kann. (2 BE)
- 5
Gegeben ist die Funktion mit und .
Weisen Sie nach, dass der Wendepunkt des Graphen von auf der Geraden mit der Gleichung liegt. (3 BE)
Der Graph von wird verschoben. Der Punkt des Graphen der Funktion besitzt nach der Verschiebung die Koordinaten . Der verschobene Graph gehört zu einer Funktion . Geben Sie eine Gleichung von an. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?