Aufgaben zur Kurvendiskussion bei gebrochen-rationalen Funktionen

Hier musst du eine Kurvendiskussion einer gebrochen-rationalen Funktion durchführen.

Definitionsbereich bestimmen

Bestimme zunächst den Definitionsbereich.

Die Nullstellen von $xx$ sind also $00$ und $33$. Daher ist der Defintionbereich von $ff$:

${\mathbb{D}}_f=\mathbb{R}\mathrm{\backslash }\{0;3\}\backslash mathbb\{D\}\_f=\backslash mathbb\{R\}\backslash backslash\backslash \{0;3\backslash \}$ .

Nullstellen

Bestimme die Nullstellen der Funktion.

Es gibt nur eine Nullstelle bei $x=-1x=-1$.

Grenzwertbetrachtung

Betrachte den Grenzwert an den Rändern des Definitionsbereichs (Intervallgrenzen, Lücken, im Unendlichen).

${\displaystyle \underset{x\to -\mathrm{\infty }}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to -\mathrm{\infty }}{\lim }\frac{\stackrel{\to 2}{\overbrace{2+\frac{2}{x}}}}{\underset{\to -\mathrm{\infty }}{\underbrace{x-3}}}=0}\backslash displaystyle\backslash lim\_\{x\; \backslash rightarrow\; -\backslash infty\}\backslash frac\{2x+2\}\{x^2-3x\}=\; \backslash lim\_\{x\; \backslash rightarrow\; -\backslash infty\}\backslash frac\{\backslash overbrace\{2+\backslash frac\{2\}\{x\}\}^\{\backslash rightarrow\; 2\}\}\{\backslash underbrace\{x-3\}\_\{\; \backslash rightarrow\; -\backslash infty\}\}=0$

${\displaystyle \underset{x\to \mathrm{\infty }}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to \mathrm{\infty }}{\lim }\frac{\stackrel{\to 2}{\overbrace{2+\frac{2}{x}}}}{\underset{\to \mathrm{\infty }}{\underbrace{x-3}}}=0}\backslash displaystyle\backslash lim\_\{x\; \backslash rightarrow\; \backslash infty\}\backslash frac\{2x+2\}\{x^2-3x\}=\; \backslash lim\_\{x\; \backslash rightarrow\; \backslash infty\}\backslash frac\{\backslash overbrace\{2+\backslash frac\{2\}\{x\}\}^\{\backslash rightarrow\; 2\}\}\{\backslash underbrace\{x-3\}\_\{\; \backslash rightarrow\; \backslash infty\}\}=0$

${\displaystyle \underset{x\to 0^{+}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 0^{+}}{\lim }\frac{\stackrel{\to 2}{\overbrace{2x+2}}}{\underset{\to 0^{-}}{\underbrace{x^2-3x}}}=-\mathrm{\infty }}\backslash displaystyle\backslash lim\_\{x\; \backslash rightarrow\; 0^+\}\backslash frac\{2x+2\}\{x^2-3x\}=\; \backslash lim\_\{x\; \backslash rightarrow\; 0^+\}\backslash frac\{\backslash overbrace\{2x+2\}^\{\backslash rightarrow\; 2\}\}\{\backslash underbrace\{x^2-3x\}\_\{\; \backslash rightarrow\; 0^-\}\}=-\backslash infty$

${\displaystyle \underset{x\to 0^{-}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 0^{-}}{\lim }\frac{\stackrel{\to 2}{\overbrace{2x+2}}}{\underset{\to 0^{+}}{\underbrace{x^2-3x}}}=\mathrm{\infty }}\backslash displaystyle\backslash lim\_\{x\; \backslash rightarrow\; 0^-\}\backslash frac\{2x+2\}\{x^2-3x\}=\; \backslash lim\_\{x\; \backslash rightarrow\; 0^-\}\backslash frac\{\backslash overbrace\{2x+2\}^\{\backslash rightarrow\; 2\}\}\{\backslash underbrace\{x^2-3x\}\_\{\; \backslash rightarrow\; 0^+\}\}=\backslash infty$

${\displaystyle \underset{x\to 3^{+}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 3^{+}}{\lim }\frac{\stackrel{\to 8}{\overbrace{2x+2}}}{\underset{\to 0^{+}}{\underbrace{x^2-3x}}}=\mathrm{\infty }}\backslash displaystyle\backslash lim\_\{x\; \backslash rightarrow\; 3^+\}\backslash frac\{2x+2\}\{x^2-3x\}=\; \backslash lim\_\{x\; \backslash rightarrow\; 3^+\}\backslash frac\{\backslash overbrace\{2x+2\}^\{\backslash rightarrow\; 8\}\}\{\backslash underbrace\{x^2-3x\}\_\{\; \backslash rightarrow\; 0^+\}\}=\backslash infty$

${\displaystyle \underset{x\to 3^{-}}{\lim }\frac{2x+2}{x^2-3x}=\underset{x\to 3^{-}}{\lim }\frac{\stackrel{\to 8}{\overbrace{2x+2}}}{\underset{\to 0^{-}}{\underbrace{x^2-3x}}}=-\mathrm{\infty }}\backslash displaystyle\backslash lim\_\{x\; \backslash rightarrow\; 3^-\}\backslash frac\{2x+2\}\{x^2-3x\}=\; \backslash lim\_\{x\; \backslash rightarrow\; 3^-\}\backslash frac\{\backslash overbrace\{2x+2\}^\{\backslash rightarrow\; 8\}\}\{\backslash underbrace\{x^2-3x\}\_\{\; \backslash rightarrow\; 0^-\}\}=-\backslash infty$

Diese Grenzwerte geben dir eine waagerechte Asymptote bei $y=0y=0$ und senkrechte Asymptoten bei $x=0x=0$ und $x=3x=3$.

Extrempunkte

Bestimme jetzt die Extrempunkte. Leite dafür die Funktion mit der Quotientenregel ab und setze sie gleich null.

${\displaystyle f(x)=\frac{2x+2}{x^2-3x}}\backslash displaystyle\; f(x)=\backslash frac\{2x+2\}\{x^2-3x\}$

${\displaystyle f^{\mathrm{\prime }}(x)=\frac{2\cdot (x^2-3x)-(2x+2)(2x-3)}{(x^2-3x{)}^2}}\backslash displaystyle\; f\text{'}(x)\; =\backslash frac\{2\backslash cdot(x^2-3x)-(2x+2)(2x-3)\}\{(x^2-3x)^2\}$

${\displaystyle f^{\mathrm{\prime }}(x)=0}\backslash displaystyle\; f\text{'}(x)\; =0$

$\iff 2\cdot (x^2-3x)-(2x+2)(2x-3)=0\backslash Leftrightarrow\; 2\backslash cdot(x^2-3x)-(2x+2)(2x-3)\; =0$

$\iff 2x^2-6x-4x^2-4x+6x+6=0\backslash Leftrightarrow\; 2x^2-6x-4x^2-4x+6x+6\; =0$

$\iff -2x^2-4x+6=0^{}\backslash Leftrightarrow-2x^2-4x+6=0^\{\; \}$

${\displaystyle x_{1;2}=\frac{4\pm \sqrt{(-4{)}^2-4\cdot (-2)\cdot (6)}}{2\cdot (-2)}=\frac{4\pm \sqrt{64}}{-4}}\backslash displaystyle\; x\_\{1;2\}\; =\backslash frac\{4\backslash pm\; \backslash sqrt\{(-4)^2-4\backslash cdot(-2)\backslash cdot(6)\}\}\{2\backslash cdot(-2)\}=\; \backslash frac\{4\backslash pm\; \backslash sqrt\{64\}\}\{-4\}$

$\Rightarrow x_1=\frac{12}{-4}=-3\backslash Rightarrow\; x\_1=\backslash frac\{12\}\{-4\}=-3$

$\Rightarrow x_2=\frac{-4}{-4}=1^{}\backslash Rightarrow\; x\_2=\backslash frac\{-4\}\{-4\}=1^\{\; \}$

Setze die Ergebnisse in die Funktion ein, um die ganzen Koordinaten zu erhalten.

${\displaystyle f(x_1)=\frac{2\cdot (-3)+2}{(-3{)}^2-3\cdot (-3)}=\frac{-4}{9+9}=-\frac{2}{9}\Rightarrow E_1(-3\mid -\frac{2}{9})}\backslash displaystyle\; f(x\_1)=\backslash frac\{2\backslash cdot(-3)+2\}\{(-3)^2-3\backslash cdot(-3)\}=\backslash frac\{-4\}\{9+9\}=-\backslash frac\{2\}\{9\}\; \backslash Rightarrow\; E\_1\backslash left(-3\backslash left|-\backslash frac\{2\}\{9\}\backslash right)\backslash right.$

$f(x_2)=\frac{2\cdot 1+2}{1^2-3\cdot 1}=\frac{4}{-2}=-2\Rightarrow E_2(1\mid -2)f(x\_2)=\backslash frac\{2\backslash cdot1+2\}\{1^2-3\backslash cdot1\}=\backslash frac\{4\}\{-2\}=-2\; \backslash Rightarrow\; E\_2\backslash left(1\backslash left|-2\backslash right)\backslash right.$

Skizze

Hier musst du eine Kurvendiskussion einer gebrochen-rationalen Funktion durchführen.

Bestimmung des Definitionsbereichs D

Bestimme den Definitionsbereich. Der vorgelegte Funktionsterm ist ein Quotient. Daher kann der Nenner $N\left(x\right)=5x-5N\backslash left(x\backslash right)=5x-5$ nicht Null werden. Da aber $\Rightarrow D=(R)\setminus 1\backslash Rightarrow\; D=\backslash mathbb(R)\backslash setminus\{1\}$

Bestimmung der Nullstellen

Um die Nullstellen zu bestimmen, musst du überlegen, wann der Zähler des Quotienten Null ist.

$Z\left(x\right)=x^2+2x+3Z\backslash left(x\backslash right)=x^2+2x+3$ den Wert Null annehmen. Also:

$x^2+2x+3=0x^2+2x+3=0$

Quadratische Gleichungen kann man mit Hilfe der quadratischen Ergänzung lösen:

$x^2+2x+3=0\iff x^2+2x=-3\iff x^2+2x+1=-3+1\iff (x+1{)}^2=-2x^2+2x+3=0\backslash Leftrightarrow\; x^2+2x=-3\backslash Leftrightarrow\; x^2+2x+1=-3+1\backslash Leftrightarrow(x+1)^2=-2$

Da Quadrate nie negativ sein können, hat $g(x)={\displaystyle \frac{x^2+2x+3}{5x-5}}g(x)=\backslash dfrac\{x^2+2x+3\}\{5x-5\}$ keine Nullstellen. Und die Definitionslücke $x_p=1x\_p=1$ ist eine Polstelle mit Vorzeichenwechsel.

Da der Zähler nie negativ wird, entscheidet nur der Nenner

$N\left(x\right)=5x-5=5(x-1)N\backslash left(x\backslash right)=5x-5=5\backslash left(x-1\backslash right)$ über das Vorzeichen von $g\left(x\right)g\backslash left(x\backslash right)$.

Links von x=1 ist und rechts von x=1 ist $g\left(x\right)>0g\backslash left(x\backslash right)>0$.

Also ${\lim }_{x\to 1_{-}}=-\mathrm{\infty }\backslash lim\_\{x\backslash rightarrow\; 1\_-\}=-\backslash infty$ und ${\lim }_{x\to 1_{+}}=\mathrm{\infty }\backslash lim\_\{x\backslash rightarrow\; 1\_+\}=\backslash infty$

Bestimmung der Asymptote

Da der Zählergrad, nämlich 2, größer als der Nennergrad, nämlich 1, ist, liegt eine schiefe Asymptote vor. Die asymtote wird durch Polynomdivision errechnet. Damit diese Polynomdivision "einfacher" klammere ich den Faktor $\frac{1}{5}\backslash frac\{1\}\{5\}$ aus.

Somit $(x^2+2x+3):(x-1)=x+3+{\displaystyle \frac{6}{x-1}}\backslash left(x^2+2x+3\backslash right):\backslash left(x-1\backslash right)=x+3+\backslash dfrac\{6\}\{x-1\}$

$\phantom{-}(x^2+2x+3):(x-1)=x+3\underset{‾}{-(x^2-x)}\phantom{-(x^2+2x}3x+3\phantom{(x^2+2x}\underset{‾}{-(3x-3)}\phantom{-(x^2+2x+}6\backslash hphantom\{-\}\backslash left(x^2+2x+3\backslash right):\backslash left(x-1\backslash right)=x+3\backslash \backslash \; \backslash underline\{-\backslash left(x^2-x\backslash right)\}\backslash \backslash \; \backslash hphantom\{-\backslash Big(x^2+2x\}3x+3\backslash \backslash \; \backslash hphantom\{\backslash Big(x^2+2x\}\backslash underline\{-\backslash left(3x-3\backslash right)\}\backslash \backslash \; \backslash hphantom\{-\backslash Big(x^2+2x+\}\backslash ;6$

Somit gilt für die Asymtote $a(x)={\displaystyle \frac{1}{5}}(x+3)a(x)=\backslash dfrac\{1\}\{5\}\backslash left(x+3\backslash right)$ und man schreibt den Term für g(x) in der Form: $g(x)={\displaystyle \frac{1}{5}}(x+3+{\displaystyle \frac{6}{x-1}})g(x)=\backslash dfrac\{1\}\{5\}\backslash left(x+3+\backslash dfrac\{6\}\{x-1\}\backslash right)$

Um die Schnittpunkte mit der Asymtote zu berechnen, setzt man g(x)=a(x).

${\displaystyle \frac{1}{5}}(x+3+{\displaystyle \frac{6}{x-1}})={\displaystyle \frac{1}{5}}(x+3)\iff 6=0\backslash dfrac\{1\}\{5\}\backslash left(x+3+\backslash dfrac\{6\}\{x-1\}\backslash right)=\backslash dfrac\{1\}\{5\}\backslash left(x+3\backslash right)\backslash Leftrightarrow\; 6=0$

Somit gibt es keinen Schnittpunkt mit der Asymptote.

Extrema

Zur Ermittlung der Extrema berechnet man die 1. Ableitung und sucht deren Nullstellen.

$g(x)={\displaystyle \frac{1}{5}}{\displaystyle \frac{x^2+2x+3}{x-1}}g(x)=\backslash dfrac\{1\}\{5\}\backslash dfrac\{x^2+2x+3\}\{x-1\}$

$\Rightarrow g^{\mathrm{\prime }}(x)={\displaystyle \frac{1}{5}}{\displaystyle \frac{(2x+2)(x-1)-1(x^2+2x+3)}{(x-1{)}^2}}={\displaystyle \frac{1}{5}}{\displaystyle \frac{2x^2+2x-2x-2-x^2-2x-3}{(x-1{)}^2}}\backslash Rightarrow\; g\text{'}(x)=\backslash dfrac\{1\}\{5\}\backslash dfrac\{(2x+2)(x-1)-1(x^2+2x+3)\}\{(x-1)^2\}=\backslash dfrac\{1\}\{5\}\backslash dfrac\{2x^2+2x-2x-2-x^2-2x-3\}\{(x-1)^2\}$

$g^{\mathrm{\prime }}(x)={\displaystyle \frac{1}{5}}{\displaystyle \frac{x^2-2x-5}{(x-1{)}^2}}g\text{'}(x)=\backslash dfrac\{1\}\{5\}\backslash dfrac\{x^2-2x-5\}\{(x-1)^2\}$

$g^{\mathrm{\prime }}(x)=0\iff x^2-2x-5=0\iff x^2-2x=5g\text{'}(x)=0\backslash Leftrightarrow\; x^2-2x-5=0\backslash Leftrightarrow\; x^2-2x=5$

$x^2-2x+1=5+1\iff (x-1{)}^2=6x^2-2x+1=5+1\backslash Leftrightarrow\; (x-1)^2=6$

$\iff x-1=\sqrt{6}\vee x-1=-\sqrt{6}\backslash Leftrightarrow\; x-1=\backslash sqrt\{6\}\; \backslash vee\; x-1=-\backslash sqrt\{6\}$

$x_1=1+\sqrt{6}\approx \mathrm{3,45}\vee x_2=1-\sqrt{6}\approx -\mathrm{1,45}x\_1=1+\backslash sqrt\{6\}\backslash approx3\{,\}45\backslash \; \backslash \; \backslash vee\backslash \; \backslash \; x\_2=1-\backslash sqrt\{6\}\backslash approx-1\{,\}45$

Graphisch ergibt sich für die vorzeichengleiche Funktion$z(x))=x^2-2x-5z(x))=x^2-2x-5$ für $g^{\mathrm{\prime }}(x)g\text{'}(x)$ eine nach oben geöffnete Parabel mit den Nullstellen $x_{1}x\_1$ und$x_{2}x\_2$

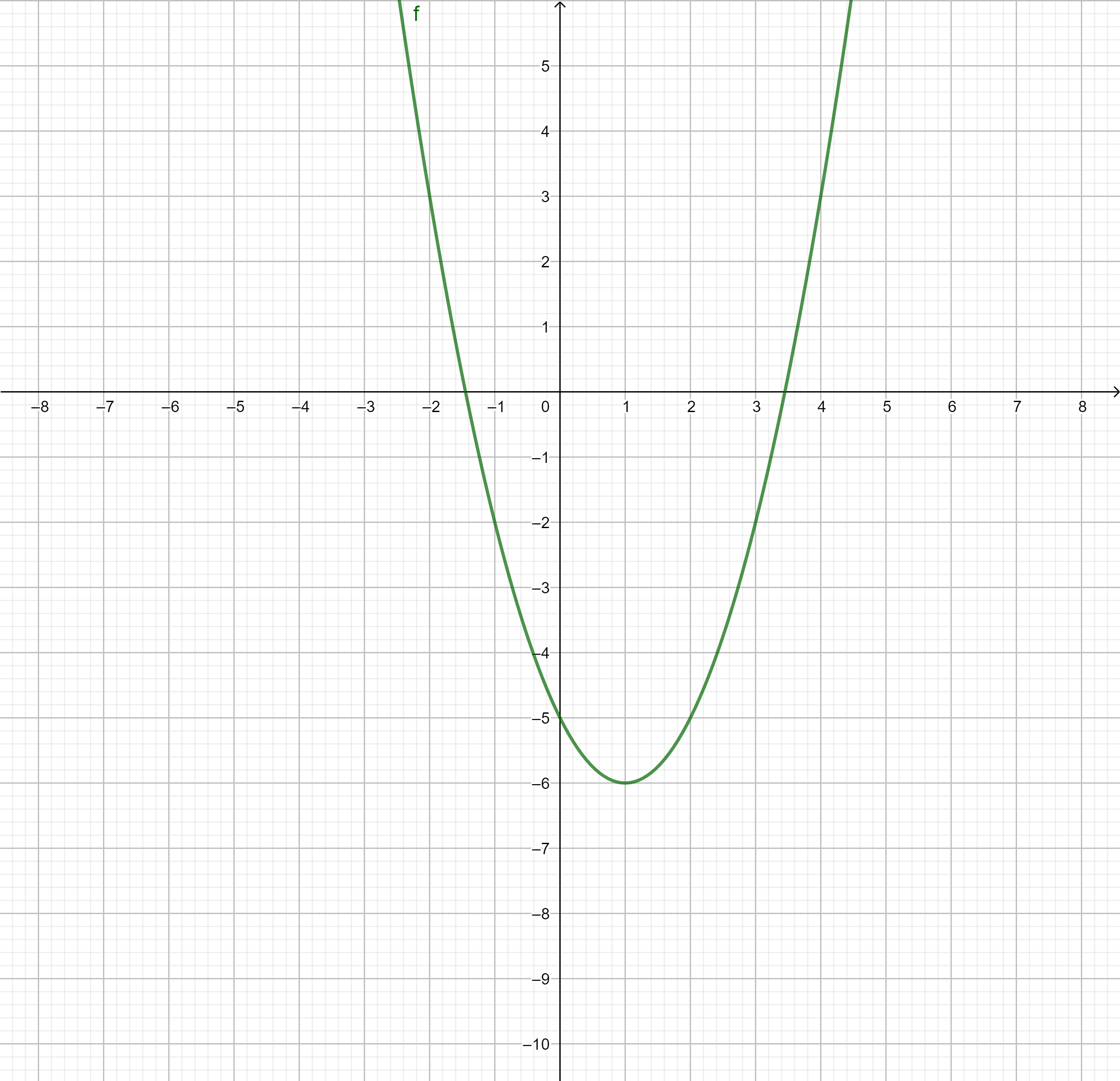
Aus dem Graphen liest man ab: links von $x_{1}x\_1$ verläuft z oberhalb der x-Achse

und zwischen $x_{1}x\_1$ und $x_{2}x\_2$ verläuft z unterhalb der x- Achse

und rechts von $x_{2}x\_2$ verläuft z oberhalb der x-Achse

Somit gilt:

• wächst

• fällt

• wächst

Also hat man ein Maximum bei $H\left(x_1\right)H\backslash left(x\_1\backslash \; \backslash right)$und ein Minimum $T\left(x_2\right)T\backslash left(x\_2\backslash right)$

Definitionsbereich bestimmen

Wir bestimmen zunächst den Definitionsbereich: Der Funktionsterm $f(x)={\displaystyle \frac{x^2}{(x-\mathrm{0,5}{)}^3}}f(x)=\backslash dfrac\{x^2\}\{(x-0\{,\}5)^3\}$ ist ein Bruch. Bei einem Bruch darf der Nenner

nicht null werden.

Ein Produkt ist genau dann gleich null, wenn wenigstens einer der Faktoren gleich null wird. Setze daher den Nenner der Funktion gleich 0, um die Definitionslücke zu bestimmen.

Nullstellenbestimmung

Die Nullstellen sind die Schnittpunkte des Funktionsgraphen mit der x-Achse.

$\Rightarrow NST=\left(0\mid 0\right)\backslash Rightarrow\backslash ;\backslash ;NST=\backslash left(0\backslash ;\backslash left|\backslash ;0\backslash right.\backslash right)$

Ableitungen bilden

1. Ableitung

$f(x)=\frac{x^2}{(x-\mathrm{0,5}{)}^3}f(x)=\backslash frac\{x^2\}\{(x-0\{,\}5)^3\}$

Berechne die Ableitungen von Zähler ($uu$) und Nenner ($vv$). Für $vv$ wird die Kettenregel verwendet.

$u^{\mathrm{\prime }}=2x,v^{\mathrm{\prime }}=3\cdot {(x-\mathrm{0,5})}^{2}u\text{'}=2x,\backslash ;v\text{'}=3\backslash cdot\backslash left(x-0\{,\}5\backslash right)^2$

Quotientenregel anwenden:

2. Ableitung

$f^{\mathrm{\prime }}\left(x\right)=-\frac{x^2+x}{{(x-\mathrm{0,5})}^4}f\text{'}\backslash left(x\backslash right)=-\backslash frac\{x^2+x\}\{\backslash left(x-0\{,\}5\backslash right)^4\}$

Berechne die Ableitungen von Zähler ($uu$) und Nenner ($vv$). Für $vv$ wird die Kettenregel verwendet.

$u^{\mathrm{\prime }}=2x+1,v^{\mathrm{\prime }}=4\cdot {(x-\mathrm{0,5})}^{3}u\text{'}=2x+1,\backslash ;v\text{'}=4\backslash cdot\backslash left(x-0\{,\}5\backslash right)^3$

Quotientenregel anwenden:

Extrema bestimmen

Für die Extrema werden mithilfe der 1. Ableitung die x-Werte bestimmt:

$f^{\mathrm{\prime }}\left(x\right)=-\frac{x^2+x}{{(x-\mathrm{0,5})}^4}f\text{'}\backslash left(x\backslash right)=-\backslash frac\{x^2+x\}\{\backslash left(x-0\{,\}5\backslash right)^4\}$

Es wird nur der Zähler der ersten Ableitung gleich 0 gesetzt, da mit dem Nenner multipliziert werden kann und dieser dann wegfällt.

Art der Extrema bestimmen

$\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ Da $f^{\mathrm{\prime }\mathrm{\prime }}(-1)>0:f\text{'}\text{'}\backslash left(-1\backslash right)>0:$ Tiefpunkt

$\Rightarrow \backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;$ Da Hochpunkt

y-Wert bestimmen

Die y-Koordinate des zweiten Extremums ist bereits bekannt, da dieses zusätzlich auch eine Nullstelle ist.

$\Rightarrow TP(-1\mid -\frac{8}{27}),HP\left(0\mid 0\right)\backslash ;\backslash ;\backslash Rightarrow\backslash ;\backslash ;TP\backslash left(-1\backslash ;\backslash left|\backslash ;-\backslash frac8\{27\}\backslash right.\backslash right),\backslash ;HP\backslash left(0\backslash ;\backslash left|\backslash ;0\backslash right.\backslash right)$