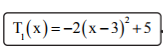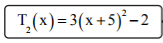2016

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Für die Arbeit eines Installateurs, die 5 Stunden dauerte, musste Frau Huber 285 € bezahlen. In dieser Rechnung sind neben dem Stundenlohn auch die Kosten für die Anfahrt enthalten, die pauschal 35 € betragen.
Welchen Betrag muss Herr Mager bezahlen, wenn er den gleichen Installateur zu denselben Bedingungen beauftragt und dieser 10 Stunden arbeitet?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Proportionalitäten beherrschen
Die Rechnung von Frau Huber in Höhe von 285 € beinhaltet neben die Arbeitszeit von 5 Stunden zusätzlich die Anfahrtspauschale von in Höhe von 35 €.
Daraus ergibt sich ein Stundenlohn in Höhe von
$(285€-35€):5= 50€$ .
Herr Mager zahlt für 10 Arbeitsstunden einschließlich Anfahrtspauschale
$10\cdot50€+35€=535€$ .
2
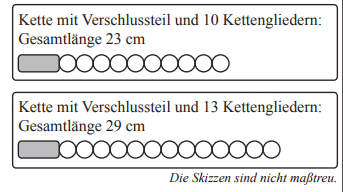
Sabine möchte eine Kette gestalten, die aus einem Verschlussteil sowie gleichartigen Kettengliedern besteht. Nebenstehend ist der Zusammenhang zwischen der Gesamtlänge möglicher Ketten (einschließlich Verschlussteil)und der Anzahl ihrer Kettenglieder dargestellt.
Ermittle, wie viele Kettenglieder für eine Kette mit einer Gesamtlänge von 57 cm erforderlich sind.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratischen Gleichungssysteme
Bezeichnungen:
$x$ bezeichnet die Länge eines Kettengliedes.
$y$ bezeichnet die Länge des Verschlussteiles.
Folgende Gleichungen gelten für die beiden Ketten:
Kette 1: $10x+y=23cm$
Kette 2: $13x+y=29cm$
Berechne zunächst die Länge eines Kettengliedes.
Löse die Gleichung von Kette 1 nach y auf.
$y=23cm-10x$
Setze das Ergebnis für $y$ in die Gleichung von Kette 2 ein.
$13x+(23cm-10x)=29cm$
$13x+23cm-10x=29cm$
$3x=6cm$
$x=2cm$
Ein Kettenglied ist $2cm$ lang.
Berechne nun die Länge des Verschlussteiles.
Setze in die Gleichung von Kette 1 das Ergebnis für $x$ ein.
$10\cdot2cm+y=23cm$
$20cm+y=23cm$
$y=3cm$
Das Verschlussteil ist $3cm$ lang.
Ermittle nun die Anzahl der Kettenglieder bei einer Kettelänge von 57cm.
$(57cm-3cm):2cm=27$
Für eine Kette mit einer Gesamlänge von $57cm$ werden $27$ Kettenglieder benötigt.
3
Fasse so weit wie möglich zusammen $\mathbb{(G = Q}).$
$3x ⋅2 + 4x ⋅2x − 4x =$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zusammenfassen von Termen
$3x\cdot2+4x\cdot2x-4x\$
$=\ 6x+8x^2-4x$
$=\ 8x^2+2x$
Beachte beim Rechnen die Punkt-vor-Strich Regel.

Bestimme die Lösungsmenge der Gleichung $3⋅(4 − 2x) = −7x −11\mathbb({G = Q)}.$

5
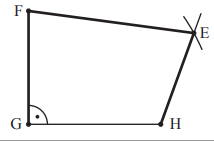
Ergänze die Zeichnung zu einem Viereck EFGH mit $∢EHG = 110°$ , $∢HGF = 90°$ ,und $GE = 5 cm$
6
Gegeben ist der Pfeil $\overrightarrow{P}=\left(\begin{matrix} -7\\8\end{matrix}\right)$ mit Fußpunkt $P\left(10{,}4\right)$ . Bestimme die Koordinaten der Spitze $Q$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelverschiebung
Bestimme die Koordinaten eines Punktes nach Verschiebung.
Gegeben:
Punkt P(10l4)
Pfeil $\overset\rightharpoonup P=\begin{pmatrix}-7\\8\end{pmatrix}$
Gesucht:
Die Koordinaten des Punktes Q
$\def\arraystretch{1.25} \begin{array}{l}Q=P+\overrightarrow{P\;}\\Q=\begin{pmatrix}10\\4\end{pmatrix}+\begin{pmatrix}-7\\8\end{pmatrix}=\begin{pmatrix}3\\12\end{pmatrix}\\\;\\\end{array}$
Der Punkt $Q$ hat die Koordinaten (3|12).
7
Das Konzert der Rockgruppe „AB/CD“ in der Stadt Hof besuchten insgesamt 1000 Personen. 80% dieser Besucher stammten aus Bayern. 60% der bayerischen Besucher kamen aus Hof. Rita behauptet, dass somit mehr als die Hälfte aller Besucher des Rockkonzerts aus Hof kamen.
Hat sie recht? Begründe.
Ja, sie hat recht.
Nein, sie hat nicht recht.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnen
Rita hat nicht recht, denn es kommen mit 480 Personen wenigerals die Hälfte aller Besucher aus Hof.
8
Bestimme die Definitionsmenge $\mathbb{D}$ und die Lösungsmenge $\mathbb{L}$ der folgenden Bruchgleichung.
$\frac13=\frac2{-5+x}$
$\mathbb{G=Q}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge einer Bruchgleichung
$\ \dfrac{1}{3}=\dfrac{2}{-5+x}$
zu a.)
Im Nenner eines Bruches darf nicht Null stehen. Alle Zahlen, für die sich beim Einsetzen in die Gleichung im Nenner Null ergibt, dürfen nicht in der Definitionsmenge enthalten sein.
Setze den Nenner gleich Null.
$\ \ -5+x=0\qquad\Rightarrow\qquad x=5$
Der Nenner wir Null bei:
$\ x=5\qquad\Rightarrow\qquad$ $D=\mathbb Q\setminus \left\{5\right\}$
zu b.)
Der Hauptnenner ist: $\ 3\cdot(-5+x)$
zu c.)
Multipliziere die Bruchgleichung mit dem HN:
$\ 1\cdot(-5+x)=2\cdot3$
zu d.)
Berechne $\text{x}$ .
$\ -5+x=\ \ 6$
$\hspace{9.5mm} x=11$
Definitionsmenge: $\ \boxed{D=\mathbb Q\setminus \left\{5\right\}}$
Lösungsmenge: $\ \ \hspace{3.2mm}\boxed{\mathbb{L}=\left\{11\right\}}$
a.) Definitionsmenge bestimmen.
b.) Bestimme den Hauptnenner.
c.) Multipliziere die Bruchgleichung mit dem HN
d.) Berechne $\text{x}$ .

Löse die Klammern auf und fasse so weit wie möglich zusammen $\mathbb{(G = Q)}.$

$(3x+2)⋅(−4+3x)=$

10
Klammere –2 aus dem gesamten Term aus $\mathbb{(G = Q)}.$
$−2x^{2} + 3x −8=$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ausklammern
Klammere $–2$ aus dem gesamten Term aus $\mathbb{(G = Q)}$
$-2x^{2}+3x-8=$
Ziehe $(-2)$ vor die Klammer, teile dann jeden Summanden in der Klammer durch $(-2)$ , also:
$−2x^2:(-2)\ =\ x^2$
$\ \ \ \ \ 3x:(-2)\ =\ -1{,}5x$
$\ \ \ \ -8:(-2)\ =\ \ 4$
in der Klammer steht dann:
$-2\cdot(x^2-1{,}5x+4)$
11
In einer Lostrommel befinden sich 100 Lose (50 Nieten, 45 Kleingewinne und 5 Hauptgewinne).Katja zieht zehnmal (zwei Kleingewinne und acht Nieten). Nun ist Tom an der Reihe und ziehteines der restlichen Lose.
Zwei der folgenden Aussagen treffen zu. Wähle diese aus.
Die Wahrscheinlichkeit, dass Tom einen Hauptgewinn zieht, ist größer als sie bei Katja war.
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, ist höher als dieWahrscheinlichkeit, dass Tom eine Niete zieht.
Die Wahrscheinlichkeit, dass Tom einen Hauptgewinn zieht, beträgt genau 5%.
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, ist größer als 50%.
Für diese Aufgabe musst du die Prozentrechnung beherrschen.
In einer Lostrommel befinden sich 100 Lose (50 Nieten, 45 Kleingewinne und 5 Hauptgewinne). Katja zieht zehnmal (zwei Kleingewinne und acht Nieten). Nun ist Tom an der Reihe und zieht eines der restlichen Lose.
Zwei der folgenden Aussagen treffen zu. Wähle diese aus.
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, ist höher als die Wahrscheinlichkeit, dass Tom eine Niete zieht.
Die Wahrschenlichkeit, dass Tom einen Hauptgewinn zieht, beträgt genau 5%.
Die Wahrscheinlichkeit, dass Tom einen Hauptgewinn zieht, ist größer als sie bei Katja war.
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, ist größer als 50%.
Als Tom zieht sind in der Lostrommel
90 Lose
42 Nieten
43 Kleingewinne
5 Hauptgewinne
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, beträgt $43:0{,}9=47{,}77$ %
Die Wahrscheinlichkeit, dass Tom eine Niete zieht, beträgt $42:0{,}9=46{,}66$ %
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, ist höher als die Wahrscheinlichkeit, dass Tom eine Niete zieht.Die Aussage ist richtig.
Die Wahrscheinlichkeit, dass Tom einen Hauptgewinn zieht, beträgt
$5:0{,}9=5{,}55$ %
Die Aussage, die Wahrscheinlichkeit, dass Tom einen Hauptgewinn zieht, beträgt genau 5% ist falsch.
Die Wahrscheinlichkeit dass Tom einen Hauptgewinn zieht, beträgt $5{,}55$ %.
Die Wahrscheinlichkeit, dass Katja einen Hauptbeginn zieht, beträgt $5:1=5%$ %
Die Aussage die Wahrscheinlichkeit, dass Tom einen Hauptgewinn zieht, ist größer als sie bei Katja war, ist richtig.
Die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, beträgt $47{,}77$ %.
Die Aussage, die Wahrscheinlichkeit, dass Tom einen Kleingewinn zieht, ist größer als 50%, ist falsch.
12
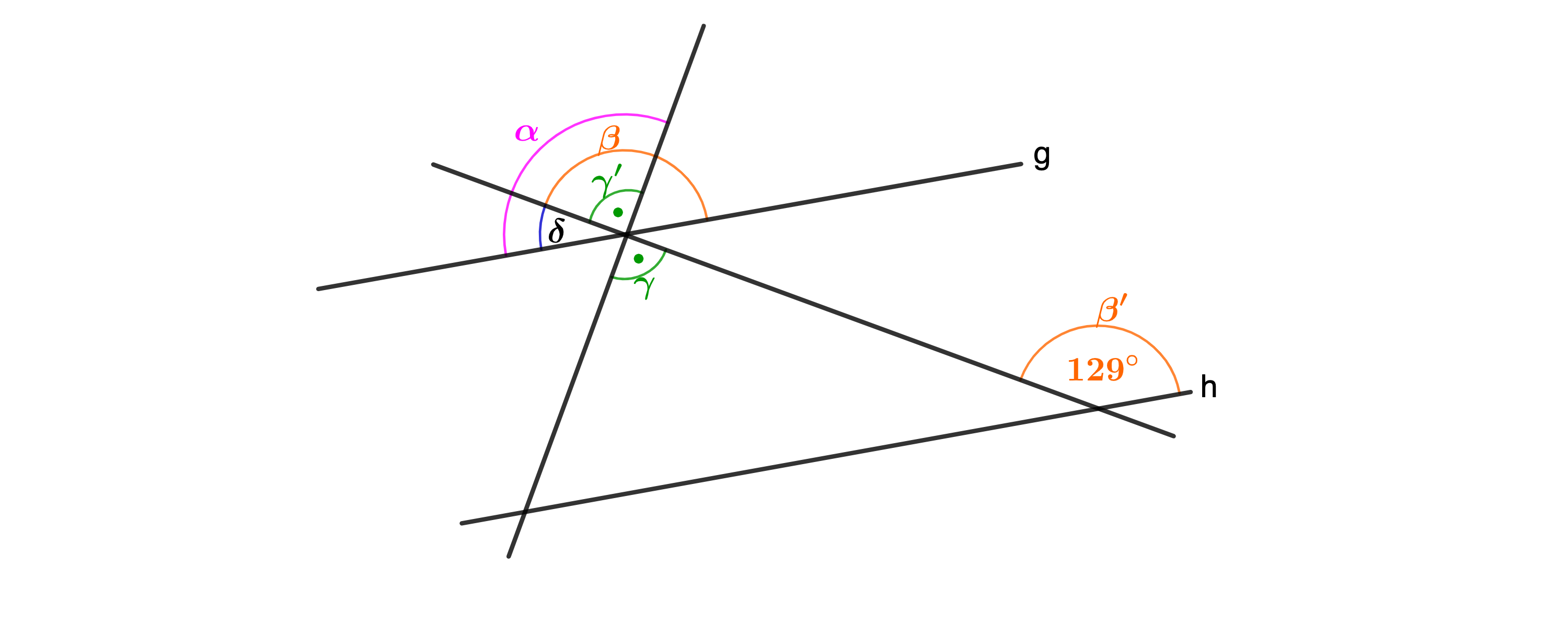
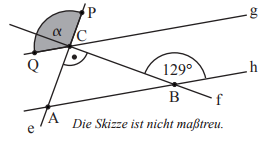
Ermittle das Maß $\alpha$ des Winkels PCQ,
wenn g || h gilt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Da die Geraden g und h parallel sind, sind $\beta$ und $\beta'$ Wechselwinkel, Wechselwinkel sind gleich groß.
Es gilt: $\beta\ =\ \beta'\ =\ 129^{\circ}$
$\gamma\ und\ \gamma'\$ sind Scheitelwinkel, Scheitelwinkel sind gleich groß.
Es gilt: $\gamma\ =\ \gamma'$ = 90 $^\circ$
$\beta\ und\ \delta\$ sind Nebenwinkel, Nebenwinkel ergänzen sich zu 180 $^\circ$ .
Es gilt: $\beta\ +\ \delta\$ = 180 $^\circ$ $\rightarrow$ $\delta\ =$ 180 $^\circ$ - 129 $^\circ$ = 51 $^\circ$
Aus der Skizze ist ersichtlich: $\alpha\ =\ \gamma'\ +\ \delta$
Der gesuchte Winkel $\alpha\ =\ 90^\circ + 51^\circ = 141^\circ$
Um $\alpha$ zu berechnen schaust du dir die Aufgabe erstmal an.
Du bemerkst sicherlich, dass es einen Stufenwinkel gibt, nämlich $\beta$ und einen Scheitelwinkel $\gamma$ welcher $90°$ besitzt.
Mit diesen Informationen kannst du jetzt ganz einfach durch berechnen anderer Winkel auf $\alpha$ kommen.
13
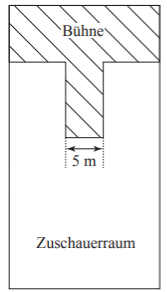
In einer Konzerthalle darf die Anzahl der Zuschauer aus Sicherheitsgründen einen bestimmten Höchstwert nicht überschreiten. Im Zuschauerraum dürfen sich deswegen höchstens vier Zuschauer pro Quadratmeter aufhalten. Der abgebildete Plan zeigt den maßstabsgetreuen Grundriss der Konzerthalle mit Bühne und Zuschauerraum.
Wie viele Zuschauer dürfen höchstens in die Konzerthalle eingelassen werden? Gib deinen Lösungsweg an.
Zuschauer
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt von Rechtecken
Durch Messen und Rechnen stellst du fest:
Der Raum ist insgesamt $4\ x\ 5\ m\ =\ 20\ m$ breit.
Der Zuschauerraum inclusive des vorspringenden Teils der Bühne ist $6\ x\ 5\ m\ =\ 30\ m$ tief.
Der Zuschauerraum inclusive des vorspringenden Teils der Bühne hat also eine Fläche von $20\ m\ x\ 30\ m\ =\ 600\ m^2$ .
Der vorspringende Teil der Bühne ist $2\ x\ 5\ m\ =\ 10\ m$ tief; er hat also eine Fläche von $5\ m\ x\ 10\ m\ =\ 50\ m^2$ .
Die Fläche des Zuschauerraums ohne den vorspringenden Teil der Bühne ist also $600\ m^2$ $\ -\ 50\ m^2$ $\ =\ 550\ m^2$ .
Pro $m^2$ dürfen sich höchstens 4 Zuschauer aufhalten, insgesamt also $4\ x\ 550\ =\ 2200$ Zuschauer.
Miss alle Längen der Skizze aus und berechne mittels Dreisatz, mit Bezug auf die angegebene Länge von 5 m, alle Längen. Berechne daraus die Fläche und zuletzt die maximale Personenzahl.
14
Zwei der folgenden Aussagen treffen zu. Wähle diese aus.
Zwei Dreiecke sind in jedem Fall kongruent (deckungsgleich), wenn sie …
… in zwei Seitenlängen und dem Maß des eingeschlossenen Winkels übereinstimme
… in drei Seitenlängen übereinstimmen
… in drei Winkelmaßen übereinstimmen.
… beide gleichseitig sind.
… beide einen rechten Winkel haben.
Für diese Aufgabe musst die Kongruenz von Dreiecken beherrschen.
Die folgenden beiden Aussagen sind richtig.
…In 3 Seitenlängen übereinstimmen.
…In 2 Seitenlängen und dem Maß des eingeschlossenen Winkels übereinstimmen.
15
Ermittle das Winkelmaß $\alpha$ , wenn gilt: $AB= BD$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel und Winkelsummen
Die Summe alle Innenwinkel eines Dreiecks beträgt $180^\circ$ .
Somit hat der Winkel $\angle CBD$ $180^\circ-(90^\circ+50^\circ)=40^\circ$ .
Der Winkel $\angle DBC$ und der Winkel $\angle ABD$ sind Nebenwinkel und ergänzen sich zu $180^\circ$ .
Der Winkel $\angle ABD$ hat also $140^\circ$ .
Da $AB=BD$ handelt es sich bei dem Dreieck $ABD$ um ein gleichschenkliges Dreieck. Die Winkel $\alpha$ und $\angle BDA$ sind also gleich.
$\alpha=(180^\circ-140^\circ):2=20^\circ$
Das Winkelmaß $\alpha=20^\circ$ .
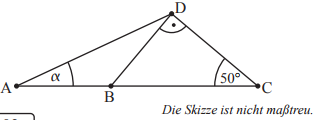
16
Es gibt Vierecke, bei denen die Diagonalen aufeinander senkrecht stehen und gleichzeitig die gegenüberliegenden Seiten zueinander parallel sind.
Kreuze die beiden Vierecksarten an, auf welche dies immer zutrifft.
Raute
Quadrat
Gleichschenkliges Trapez
Drachenviereck
Parallelogramm
Rechteck
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierecke
Füge hier gerne eine Lösung hinzu!
17
Vervollständige die Wertetabellen jeweils so, dass x und y zueinander …
1. ... direkt proportional sind.
  x
  1
  2
  y
  6
  24
  
  Aus der zweiten Spalte folgt: $C=\dfrac{y}{x}=\dfrac{6}{2}=3$ .
  1. Spalte: Für $x=1$ folgt $y=C\cdot x=3\cdot 1=3$ .
  3. Spalte: Für $y=24$ folgt $x=\dfrac{y}{C}=\dfrac{24}{3}=8$ .
  Siehe Tabelle.
  x
  1
  2
  8
  y
  3
  6
  24
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bei der direkten Proportionalität zweier Größen ist das Verhältnis dieser Größen - also ihr Quotient - immer gleich. Es ist $C=\dfrac{y}{x}$ . Dabei ist $x$ die Grundgröß und $y$ die zugeordnet Größe
2. ... indirekt proportional sind.
  x
  1
  2
  y
  12
  6
  24
  
  Hier ist $y\cdot x=1\cdot12=12$ bzw. $y\cdot x=2\cdot 6=12$ , d.h. $C=12$ .
  Entsprechend erhält man $x=\dfrac{C}{y}=\dfrac{12}{24}=\dfrac{1}{2}=0{,}5$ .
  Siehe Tabelle.
  x
  1
  2
  0,5
  y
  12
  6
  24
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bei der indirekten Proportionalität (umgekehrte Proportionalität, Antiproportionalität) ist das Produkt zweier Größen immer konstant. Dieses Produkt wird als Proportionalitätskonstante bezeichnet und es gilt:
  $y\cdot x=C$ oder $y=\dfrac{C}{x}$ oder $x=\dfrac{C}{y}$ .
18
Das Volumen eines Quaders mit der Länge 1 cm, der Breite 2 cm und der Höhe 10 cm soll aufdas Dreifache vergrößert werden.Wie können Länge, Breite und Höhe verändert werden, um dies zu erreichen?
Wähle die beiden richtigen Möglichkeiten aus.
Man verlängert die Höhe auf das Doppelte und die Breite auf das 1,5-fache bei gleichbleibender Länge.
Man verdreifacht die Breite bei unveränderter Höhe und unveränderter Länge
Man verdoppelt die Länge sowie die Breite und halbiert die Höhe.
Man verdreifacht gleichzeitig die Länge, die Breite und die Höhe.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung eines Quaders
$V=l\cdot b\cdot h$
Gegeben ist ein Quader mit dem Volumen
$V=1cm\cdot2cm\cdot10cm=20cm^3$
Gesucht ist ein Quader mit dem 3-fachen Volumen, also
$V=60cm^3$
Aussage 1: Länge und Höhe bleiben gleich. Die Breite wird verdreifacht.
$V=1cm\cdot3\cdot2cm\cdot10cm=60cm^3$
Aussage 2: Gleiche Länge, 1,5 fache Breite und doppelte Höhe
$V=1cm\cdot1{,}5\cdot2cm\cdot20cm=60cm^3$
Aussage 3: 3-fache Länge, 3-fache Breite, 3-fache Höhe
$V=3\cdot1cm\cdot3\cdot2cm\cdot3\cdot10cm=540cm^3$
Aussage 4: Doppelte Länge, doppelte Breite, halbe Höhe
$V=2\cdot1cm\cdot2\cdot2cm\cdot\frac12\cdot10cm=40cm^3$
Die beiden Aussagen
Aussage 1: Länge und Höhe bleiben gleich. Die Breite wird verdreifacht.
$V=1cm\cdot3\cdot2cm\cdot10cm=60cm^3$
Aussage 2: Gleiche Länge, 1,5 fache Breite und doppelte Höhe
$V=1cm\cdot1{,}5\cdot2cm\cdot20cm=60cm^3$
liefern einen Quader der das dreifache Volumen des ursprünglichen Quaders hat.
19
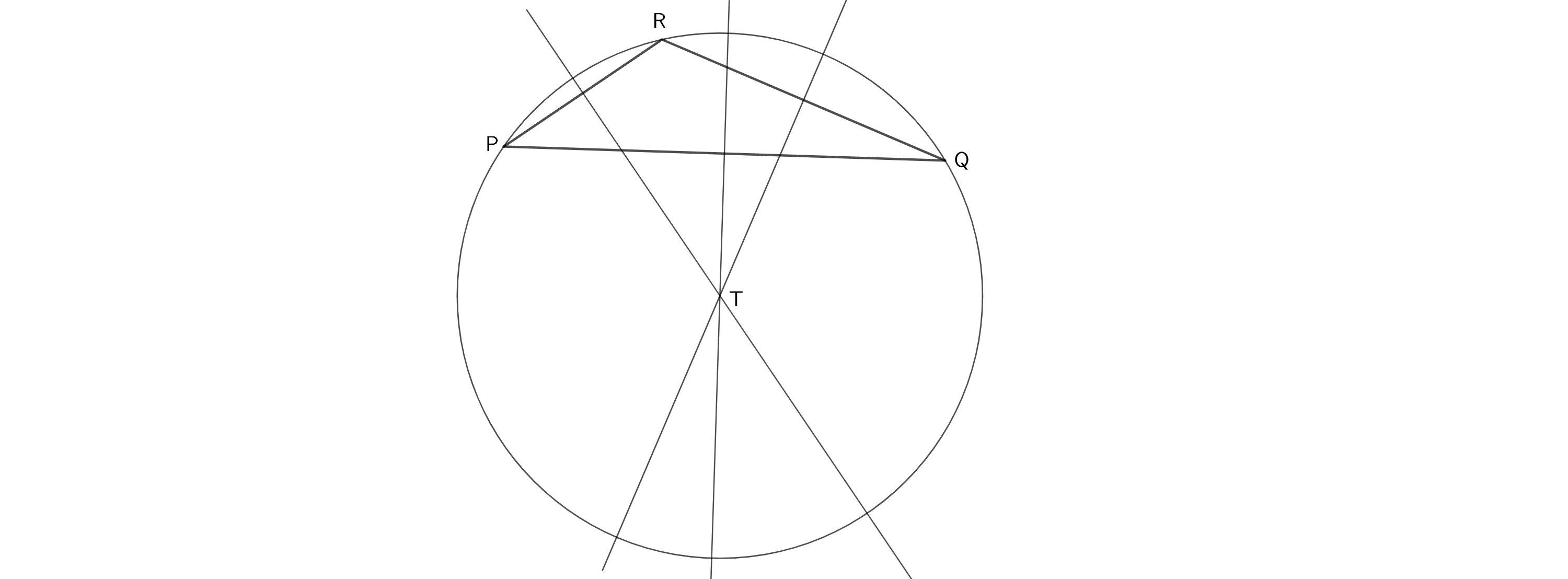
Ermittle durch Konstruktion den Punkt T, der von den Punkten P, Q und R gleich weit entfernt ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion eines Punktes
Verbinde die Punkte $PQR$ zu einem Dreieck. Errichte die Mittelsenkrechten auf den drei Seiten. Der Schnittpunkt $T$ der Mittelsenkrechten ist der Mittelpunkt des Umkreises des Dreiecks $PQR$ .
Die Punkte $P;\ Q;\ R;$ liegen auf dem Umkreis des Dreiecks $PQR\ \Rightarrow\overline{TP}=\overline{TQ}=\overline{TR}$
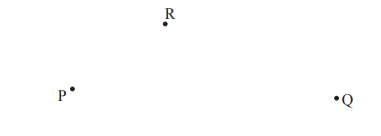
20
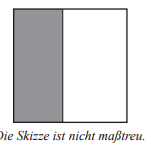
Ein Quadrat mit einer Seitenlänge von 10 cm wird in zwei Rechtecke geteilt, von denen eines einen Umfang von 26 cm hat.
Welchen Flächeninhalt hat dieses Rechteck?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalte von Rechtecken
$U_{Rechteck}=2a+2b$
Bekannt sind $a=10cm$ und $U_{Rechteck}=26cm$ .
$26cm=20cm+2b$
$b=3cm$
$A_{Rechteck}=a\cdot b$
$A_{Rechteck}=10cm\cdot3cm=30cm²$
Der Flächeninhalt des Rechtecks beträgt $30cm²$ .
21
Gegeben sind die beiden quadratischen Terme $T1(x)$ und $T2(x) \mathbb{(G = Q)}$ . Ordne den beiden Termen jeweils den passenden Extremwert mit der zugehörigenBelegung von x zu,+.
Wähle dazu zusammengehörige Kästchen.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwerte einer Funktion
  Für diese Aufgabe musst du wissen, wie man die Extremwerte einer Funktion berechnet.
  Gegeben ist die Funktion
  $T_1(x)=-2(x-3)^2+5^{}$
  $T_1(x)=-2(x^2-6x+9)+5=-2x^2+12x-18+5=-2x^2+12x-13$
  Bestimme das Extremum mit Hiilfe der 1. Ableitung.
  $T'_1(x)=-4x+12$
  $\def\arraystretch{1.25} \begin{array}{l}T'_1(0)=0\;=>\;\\0=-4x+12\;=>\\4x=12\;=>\\x=3\end{array}$
  $x_E=3$
  Bestimme die Art des Extremums mit Hilfe der 2. Ableitung.
  $T''_1(x)=-4$
  $T''_1(x_E)=-4>0$
  Der Extremwert ist ein Maximum.
  Bestimme die $y$ Koordinate des Extremums.
  Setze $x_E$ in $T_1(x)$ ein.
  $T_1(3)=-2(3-3)^2+5=5$
  $T_{max}=5\;\;für\;\;x=3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwerte einer Funktion
  Gegeben ist die Funktion
  $T_2(x)=3(x+5)^2-2^{}$
  $T_2(x)=3(x^2+10x+25)-2=3x^2+30x+75+-2=3x^2+30x+73$
  Bestimme das Extremum mit Hilfe der 1. Ableitung.
  $T'_2(x)=6x+30$
  $\def\arraystretch{1.25} \begin{array}{l}T'_2(0)=0\;=>\;\\0=6x+30\;=>\\6x=-30\;=>\\x=-5\end{array}$
  $x_E=-5$
  Bestimme die Art des Extremums mit Hilfe der 2. Ableitung.
  $T''_2(x)=6$
  $T''_2(x_E)=6>0$
  Der Extremwert ist ein Minimum.
  Bestimme die $y$ -Koordinate des Extremums.
  Setze $x_E$ in $T_2(x)$ ein.
  $T_2(-5)=3(-5+5)^2-2=-2$
  $T_{min}=-2\;\;\text{für}\;\;x=-5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

x	1	2
y		6	24

x	1	2	8
y	3	6	24

x	1	2
y	12	6	24

x	1	2	0,5
y	12	6	24

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 3\cdot(4-2x)$	$=$	$\displaystyle -7x-11$
	↓	Löse zunächst die Klammer auf.
$\displaystyle 12-6x$	$=$	$\displaystyle -7x-11$	$\displaystyle +7x$
$\displaystyle 12+x$	$=$	$\displaystyle -11$	$\displaystyle -12$
$\displaystyle x$	$=$	$\displaystyle -23$

	$\displaystyle \left(3x+2\right)\cdot\left(-4+3x\right)$
	↓ Klammern ausmultiplizieren, beachte die Vorzeichen
$=$	$\displaystyle 3x\cdot -4 +3x\cdot 3x +2\cdot -4 + 2\cdot 3x$
	↓ Vereinfachen
$=$	$\displaystyle -12x+9x^2-8+6x$
	↓ Zusammenfassen
$=$	$\displaystyle 9x^2-6x-8$

2016

Gegeben:

Gesucht:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?