Teil B, Gruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
- 2
Ein Kegel hat die Körperhöhe = 24cm.Die Grundfläche hat den Radius r = 10 cm. (4 Punkte)
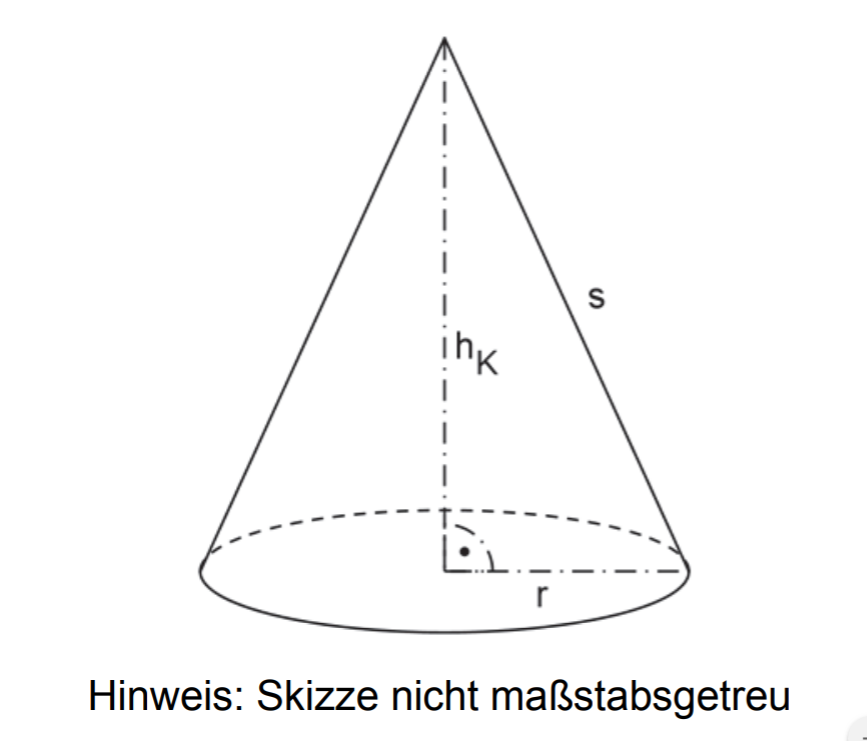
Berechne das Volumen des Kegels.
Ermittle rechnerisch die Länge der Mantellinie s des Kegels.
Ein anderer Kegel hat eine Grundfläche mit einem Flächeninhalt von G = cm .
Berechne den Umfang der Grundfläche des zweiten Kegels.
- 3
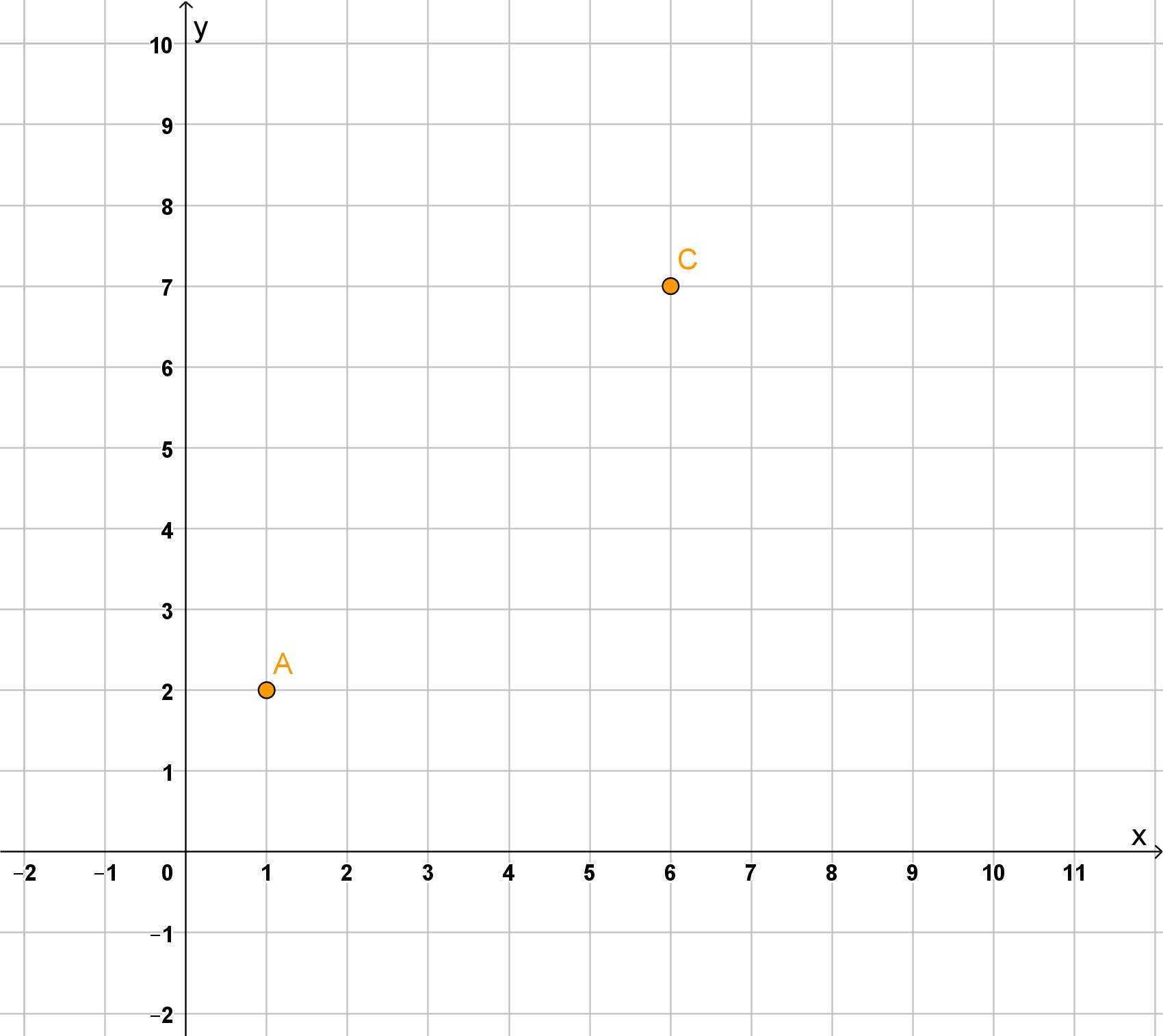
Zeichne in ein Koordinatensystem (Einheit: ): (4 Punkte)
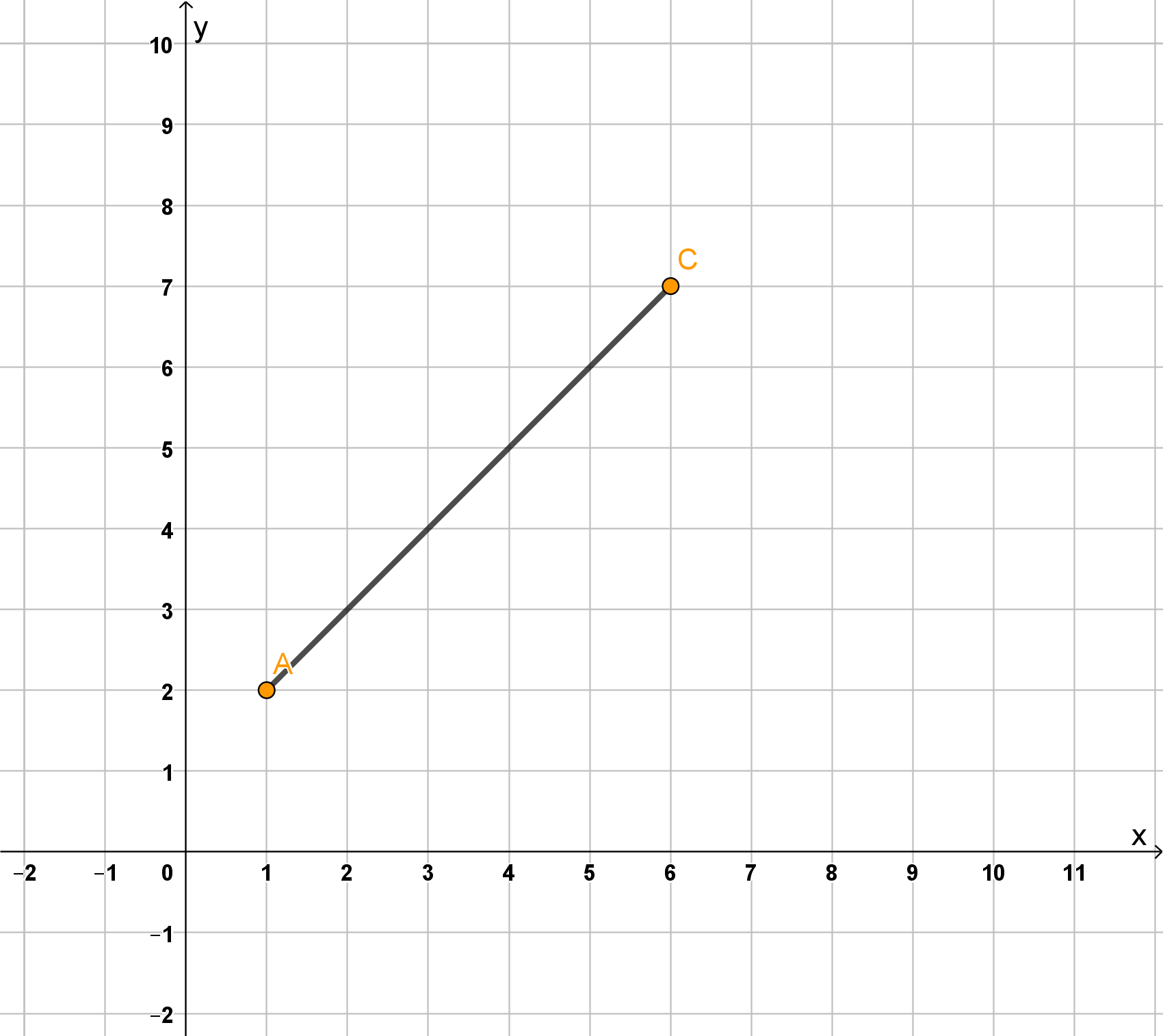
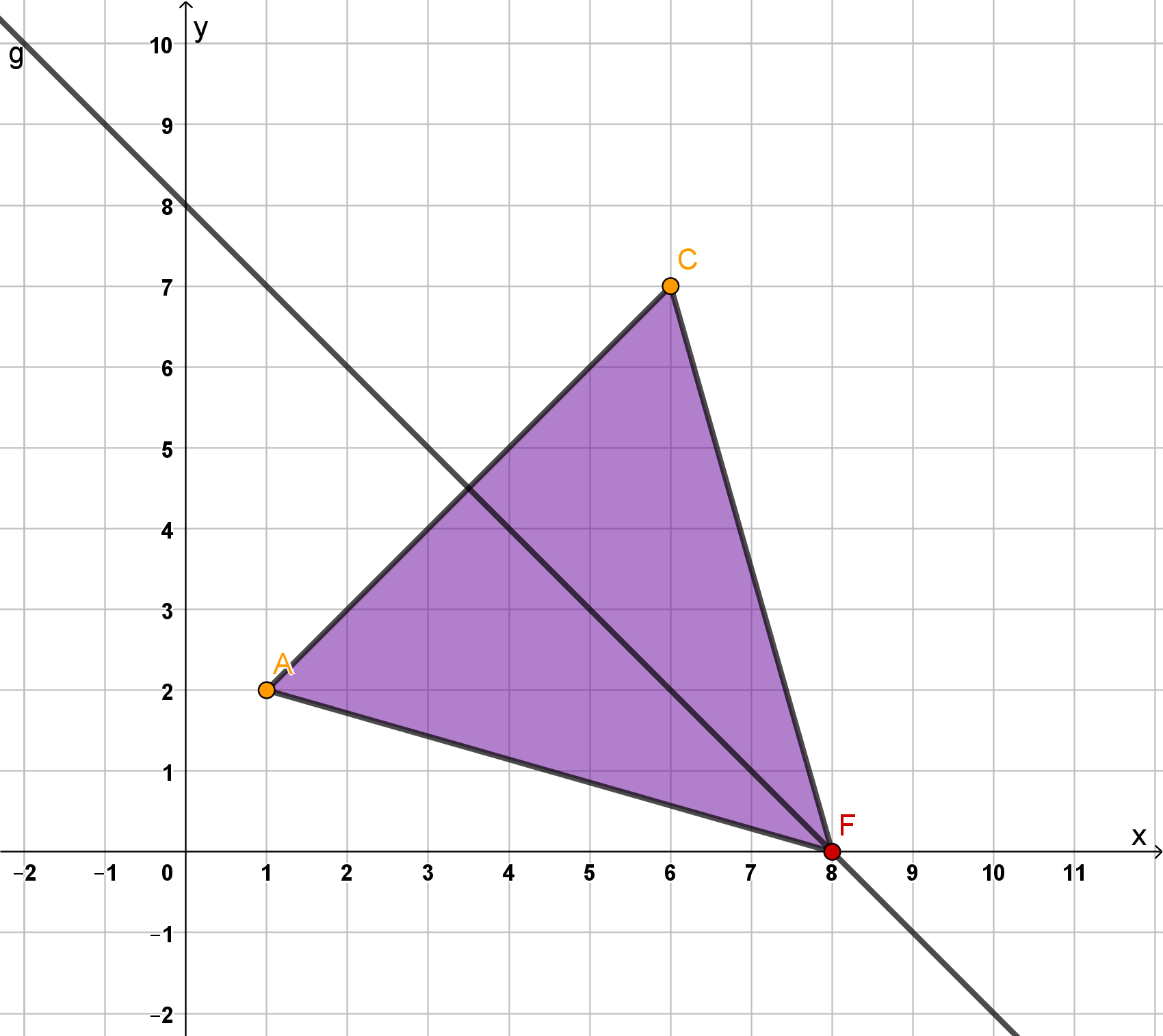
Zeichne die Punkte und ein und verbinde sie zur Strecke .
(Hinweis zum Platzbedarf: x-Achse von bis , y-Achse von bis )
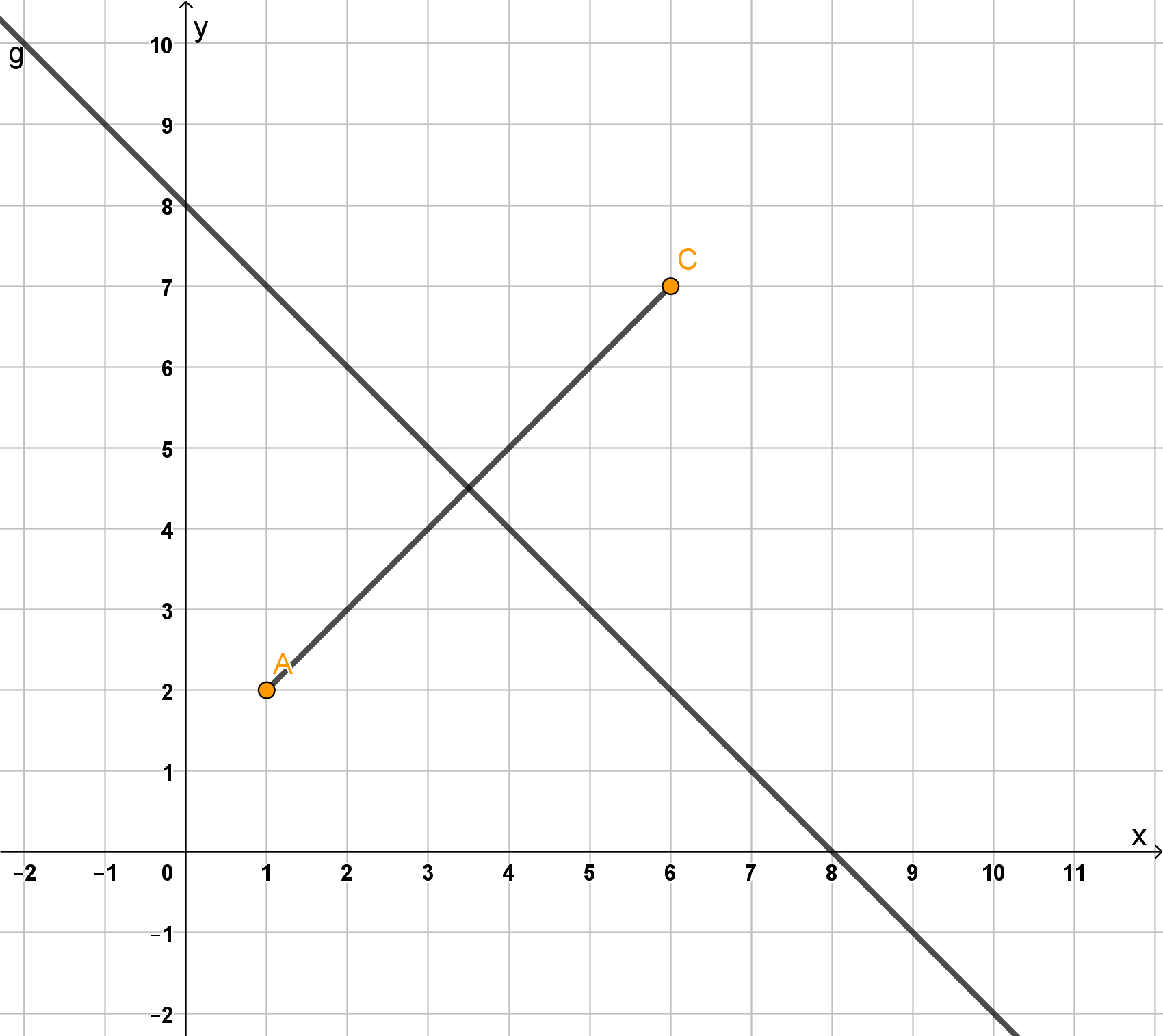
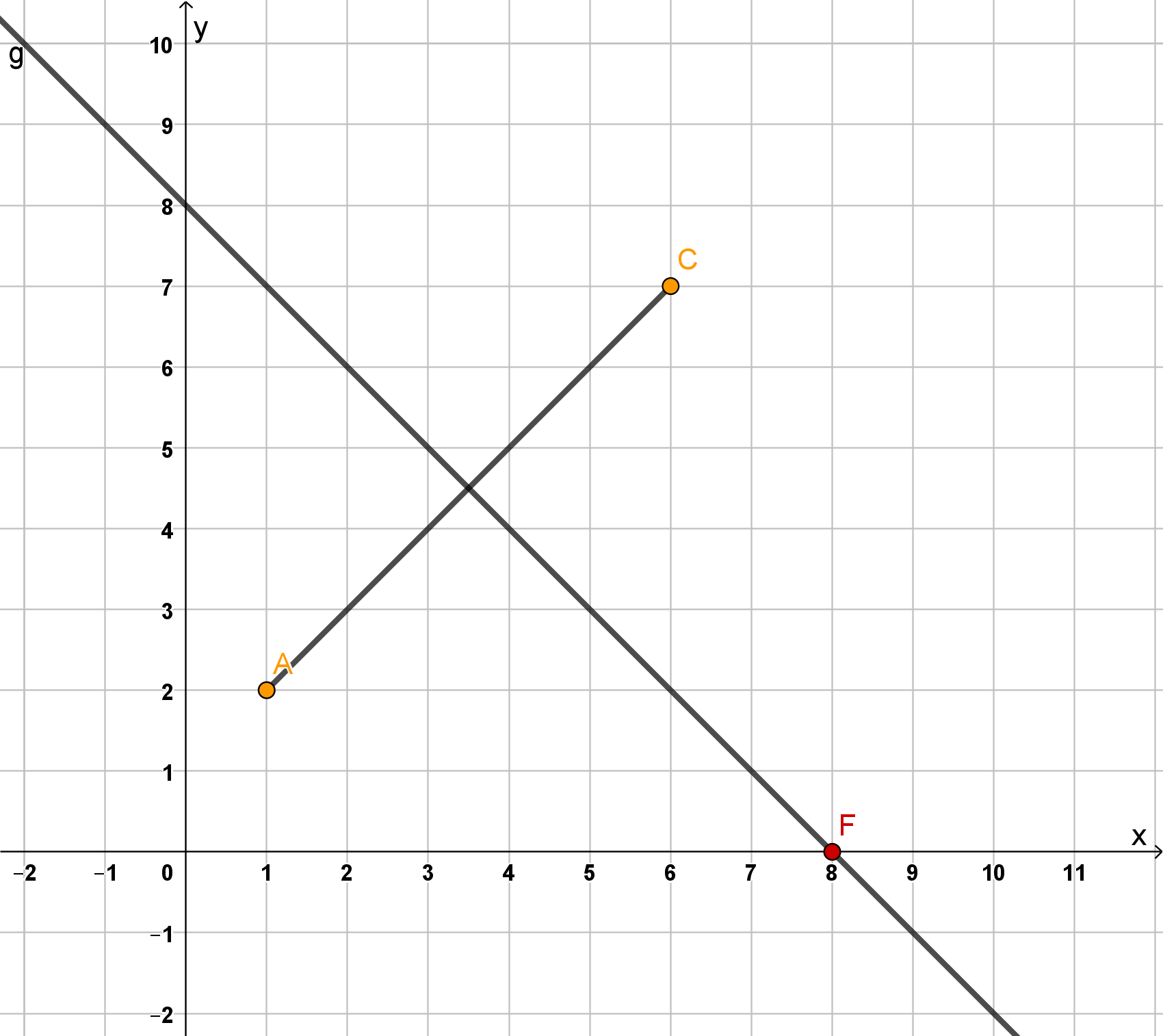
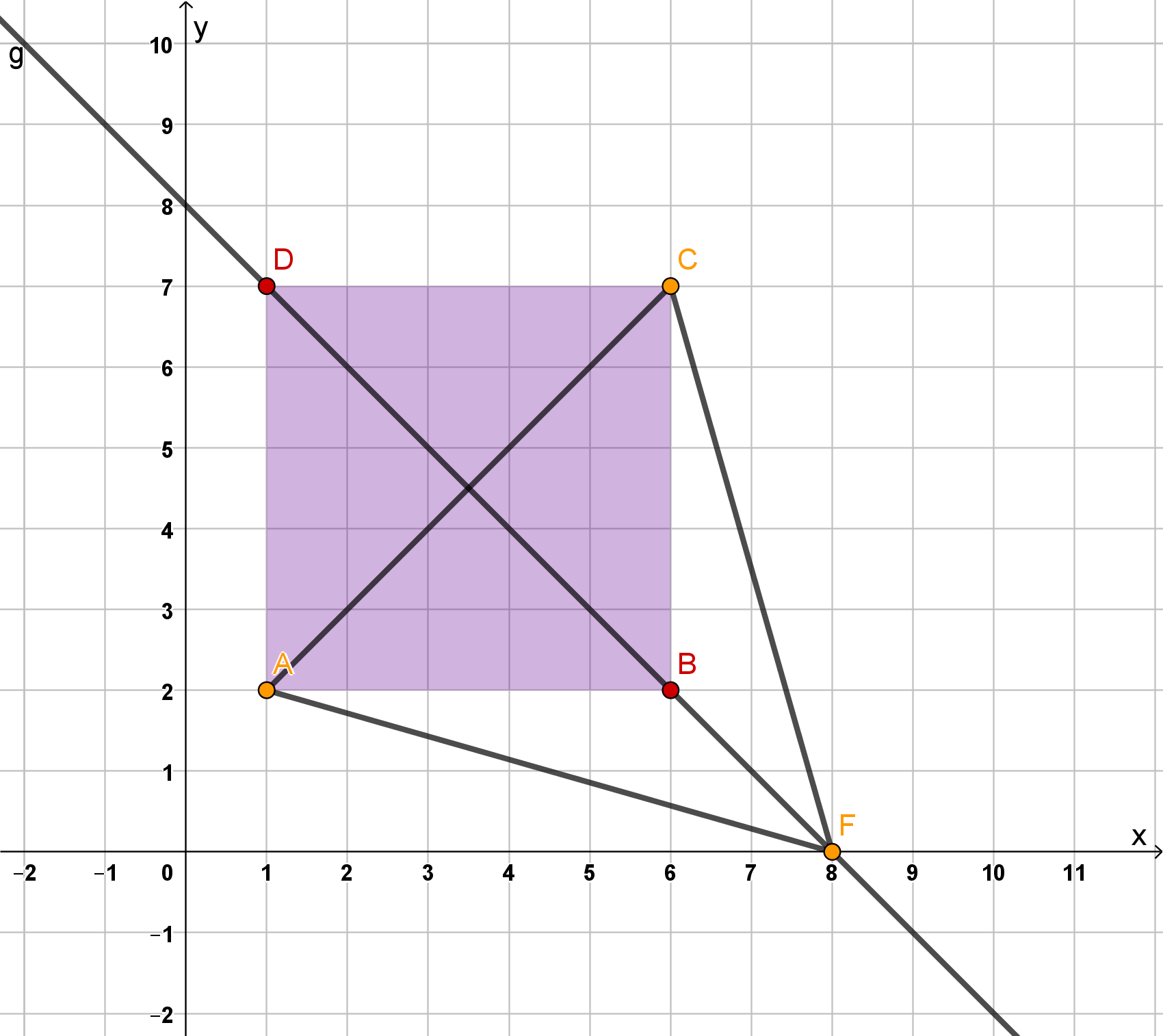
Zeichne ein gleichschenkliges Dreieck mit der Basis []. Der Punkt soll auf der x-Achse des Koordinatensystems liegen.
Die Strecke [] ist eine Diagonale des Quadrats . Zeichne dieses Quadrat und beschrifte es.
- 4
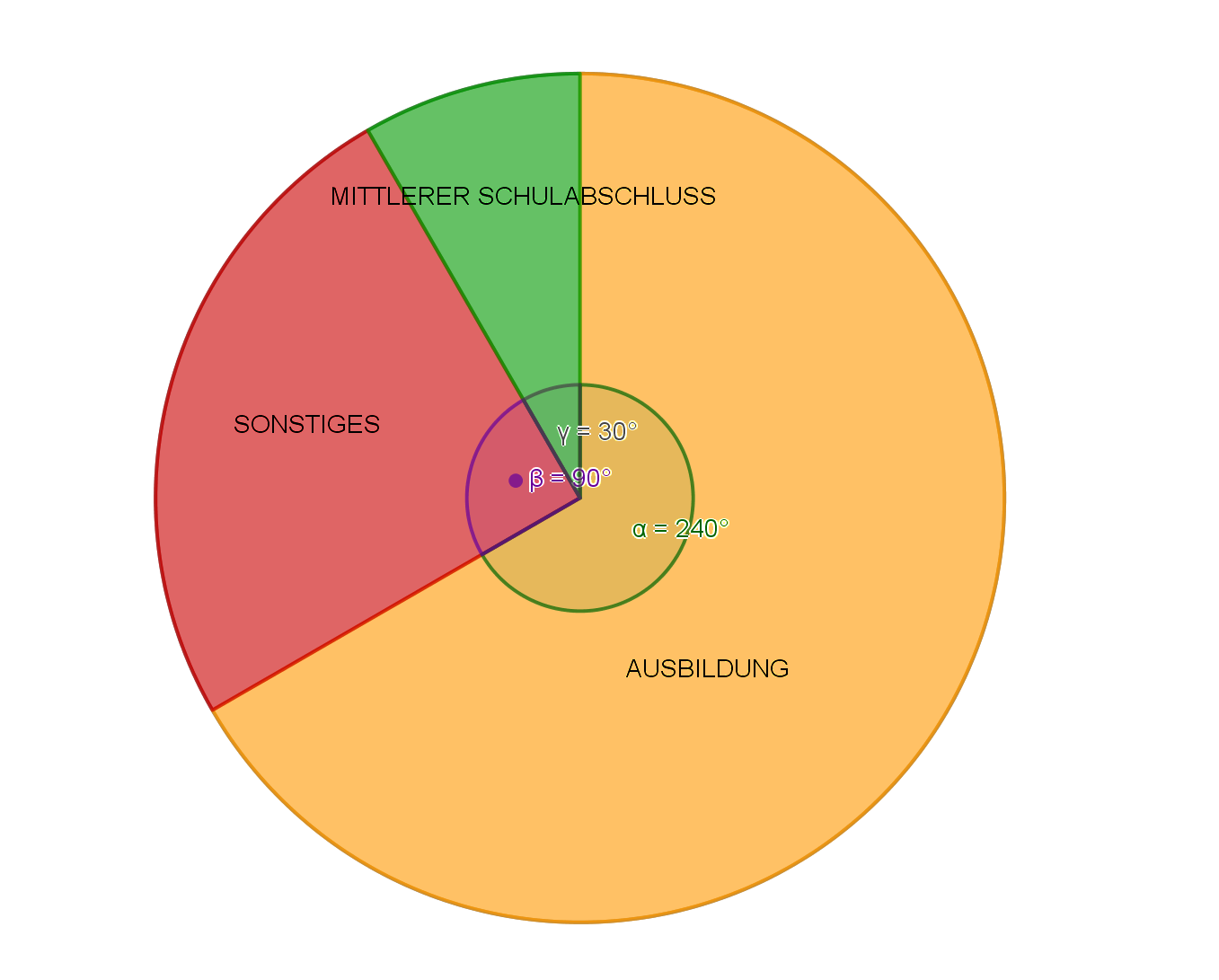
Die insgesamt 51 Schülerinnen und Schüler der 9. Klassen einer Mittelschule wurden zu ihren Plänen nach dem Abschluss befragt.

Gib die Anzahl der Schülerinnen und Schüler der Klasse 9a an, die einen mittleren Schulabschluss erwerben wollen.
Berechne, um wie viel Prozent die Anzahl der Jugendlichen, die eine Ausbildung beginnen wollen, in Klasse 9a größer ist als in Klasse 9b.
Stelle die Angaben der Klasse 9b in einem Kreisdiagramm (Radius r = 6 cm) dar.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?