Teil B, Gruppe 3
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Die Händler A, B, C und D beliefern eine Nudelfabrik mit insgesamt 48 700 Eiern.
Händler B liefert 4600 Eier mehr als Händler A. Händler C liefert doppelt so viele Eier wie Händler B. Händler D bringt 4100 Eier.
Wie viele Eier liefert jeder Händler an?
Löse mithilfe einer Gleichung. (4 Punkte)
- 2
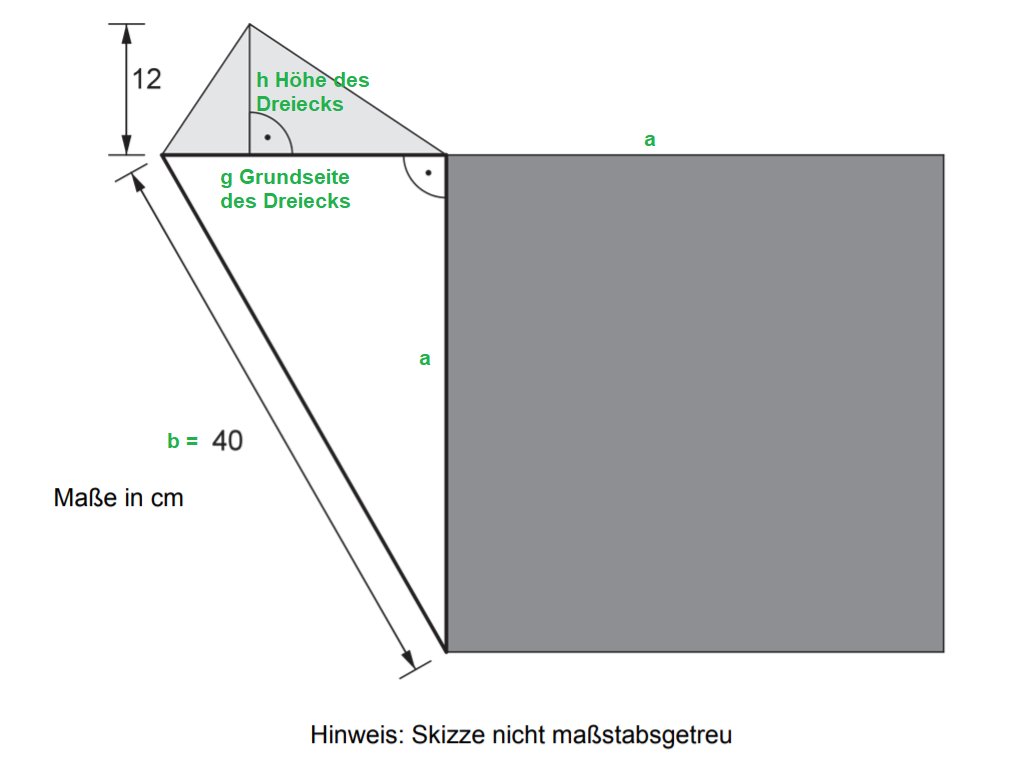
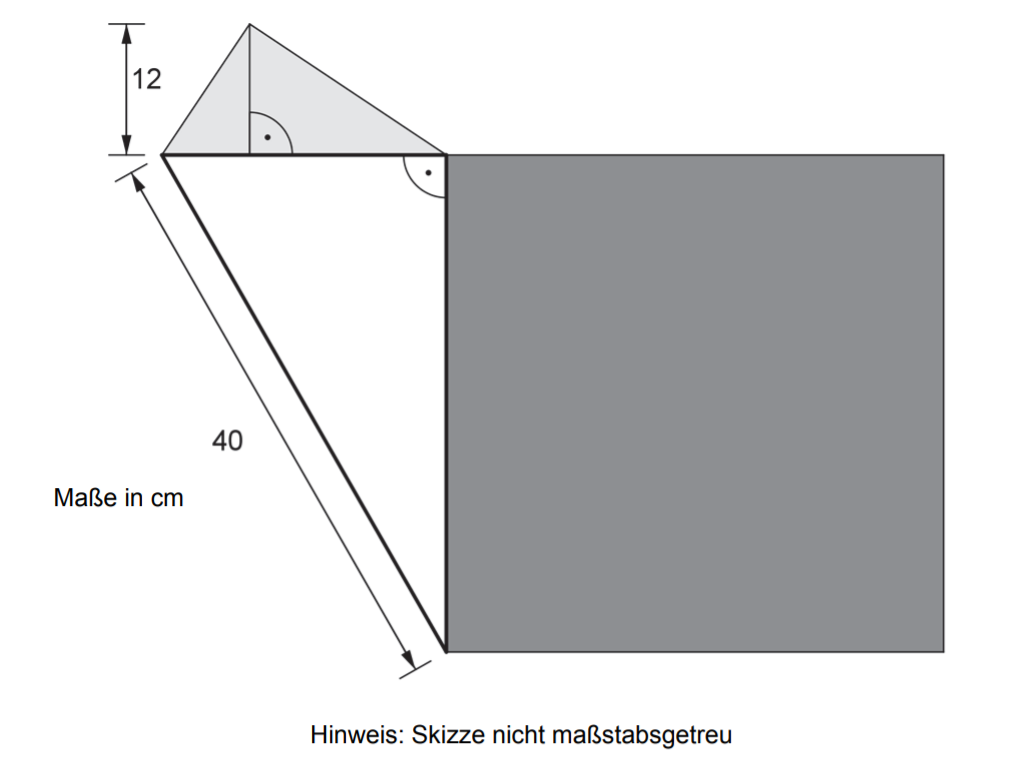
Der Flächeninhalt des hellgrauen Dreiecks beträgt 144 cm².Berechne den Flächeninhalt und den Umfang des dunkelgrauen Quadrats. (4 Punkte)
- 3
Aus 1350 kg Äpfeln werden 500 l Apfelsaft hergestellt. (4 Punkte)
Berechne, wie viele kg Äpfel man für 35 l Apfelsaft benötigt.
Ermittle, wie viele Liter Apfelsaft man aus 540 kg Äpfeln herstellen kann.
35 l Apfelsaft werden in Flaschen zu je 0,7 l abgefüllt. In eine Getränkekiste passen 12 dieser Flaschen. Gib an, wie viele volle Getränkekisten diese 35 l Apfelsaft ergeben.
- 4
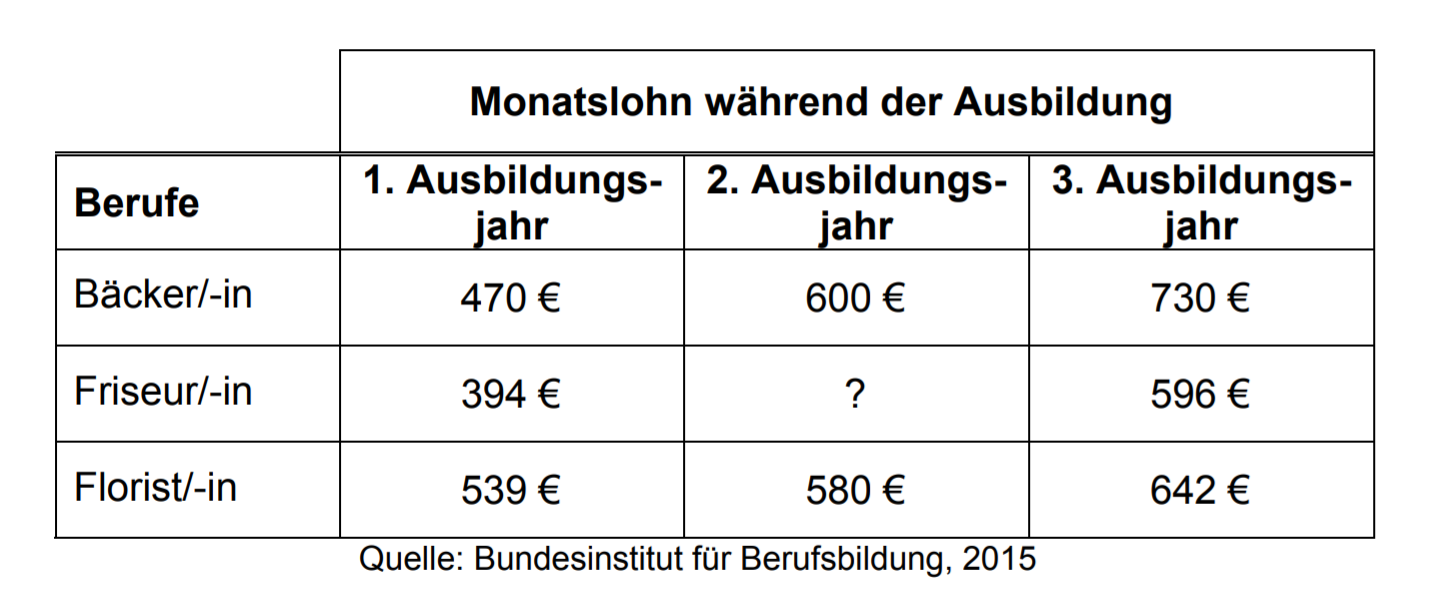
Bild zur Aufgabe
Berechne den durchschnittlichen Monatslohn einer Floristin in den drei Ausbildungsjahren.
Ermittle, wie viel Prozent ein Bäcker im 2. Ausbildungsjahr mehr verdient als im 1. Ausbildungsjahr.
Der Monatslohn eines Friseurs ist im 3. Ausbildungsjahr um 21 % höher als im 2. Ausbildungsjahr. Berechne seinen Monatslohn im 2. Ausbildungsjahr. Runde auf ganze Euro.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?