Aufgaben zu Extremwertproblemen aus der Geometrie
Hier findest du Aufgaben zu Extremwertproblemen aus der Geometrie. Schaffst du sie alle?
- 1
Auf einem Bauernhof möchte der Bauer eine rechteckige Koppel für seine Pferde anlegen.
Die Koppel liegt an einem Fluss und soll deshalb nur an drei Seiten eingezäunt werden.
Der zur Verfügung stehende Zaun ist 120m lang.
Wie muss der Bauer die Koppel anlegen, damit sie eine möglichst große Weidefläche hat?
Wie groß ist die Weidefläche dieser Koppel?
- 2

Die Gemeinde Haar weist neues Bauland aus.
Herr Meier hat die dreieckige Fläche gekauft, muss aber nun (wie vorgeschrieben) ein rechteckiges Baugrundstück festlegen.
Wie sollte sich Herr Meier entscheiden, wenn er ein möglichst großes Baugrundstück haben will?
- 3
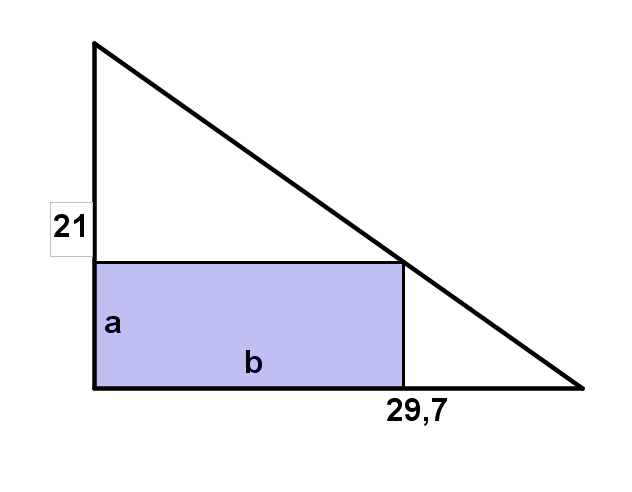
Aus einem diagonal halbierten DIN A4 Blatt soll entsprechend der Zeichnung ein möglichst großflächiges Rechteck geschnitten werden.
Finde die Breite a, für die der Flächeninhalt des Rechtecks maximal ist.
- 4
Aus einem langen Draht soll das Kantenmodell einer quadratischen Säule hergestellt werden.
Wie lang sind die Kanten zu wählen, damit die Säule maximales Volumen hat?
ist die Kantenlänge. - 5
Aus einem 120cm langen Draht ist das Kantenmodell eines Quaders herzustellen, so dass eine Kante dreimal so lang wie eine andere und der Rauminhalt maximal ist.
Wie lang sind die Kanten zu wählen?
- 6
Eine oben offene zylinderförmige Dose mit dem Volumen V soll aus Blech hergestellt werden. Dabei soll der Blechverbrauch möglichst gering sein. Bestimme die Höhe und den Durchmesser der Dose, sowie den minimalen Blechverbrauch.
- 7
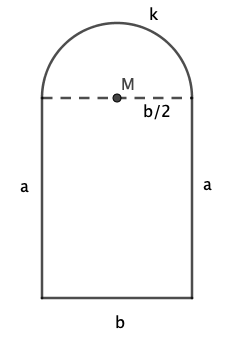
Eine romanische Fensterform ist zusammengesetzt aus einem Rechteck und einem oben anschließenden Halbkreis.
Das nebenstehende romanische Fenster habe den Umfang und die Rechtecksseiten und .
Bei welchen Werten für und hat das Fenster den größtmöglichen Flächeninhalt?
- 8
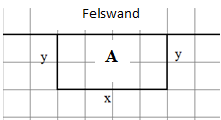
Ein Schäfer möchte für seine Schafe eine rechteckige Weidefläche mit einem Zaun begrenzen.
Die Weidefläche grenzt direkt an eine Felswand.
Der Schäfer hat insgesamt je lange zusammensteckbare Zaunelemente zur Verfügung.

Ermittle die Abmessungen und so, dass die abgesteckte Fläche einen maximalen Flächeninhalt hat.
Quellen
Abb 1: https://pixabay.com/de/schaf-berg-ranch-japan-zaun-680217/
- 9
Schultüten
Jana und Nish basteln zu ihrer Einschulung Schultüten.
Ihre Eltern haben ihnen bereits rundes dickes Papier bereit gelegt, mit einem Radius von .
Dieses malen sie bunt an und schneiden einen Kreissektor aus dem Papier aus, um einen Kegel zu formen.
Jana schneidet einen Kreissektor mit dem Mittelpunktswinkel aus. Nish wählt für seine Schultüte .

Jana ist der Meinung, dass in ihre Tüte doppelt so viel Inhalt passt wie in Nishs Tüte, da sie einen doppelt so großen Winkel gewählt hat. Berechne, ob Jana mit ihrer Annahme richtig liegt.
Lina kommt später zum Basteln dazu und bekommt die Diskussion zwischen Nish und Jana mit. Sie möchte beide übertrumpfen und eine Schultüte basteln, in die am meisten Süßes rein passt. Sie benutzt ein übriges rundes Papier mit und schneidet einen Kreissektor mit Mittelpunktswinkel aus dem Papier aus. Bestimme den Winkel , für den das Kegelvolumen maximal wird.
Beurteile an Hand von Durchmesser und Höhe des Kegels, ob sich die gebastelten Kegelmäntel auch als Schultüten eignen.
- 10
Ein Bauer will eine neue Weide in Form eines Rechtecks anlegen. Die eine Seite grenzt aber bereits an die lange Scheune an. Der Bauer hat Zaun zur Verfügung und möchte eine Fläche mit dem größtmöglichen Flächeninhalt einzäunen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?