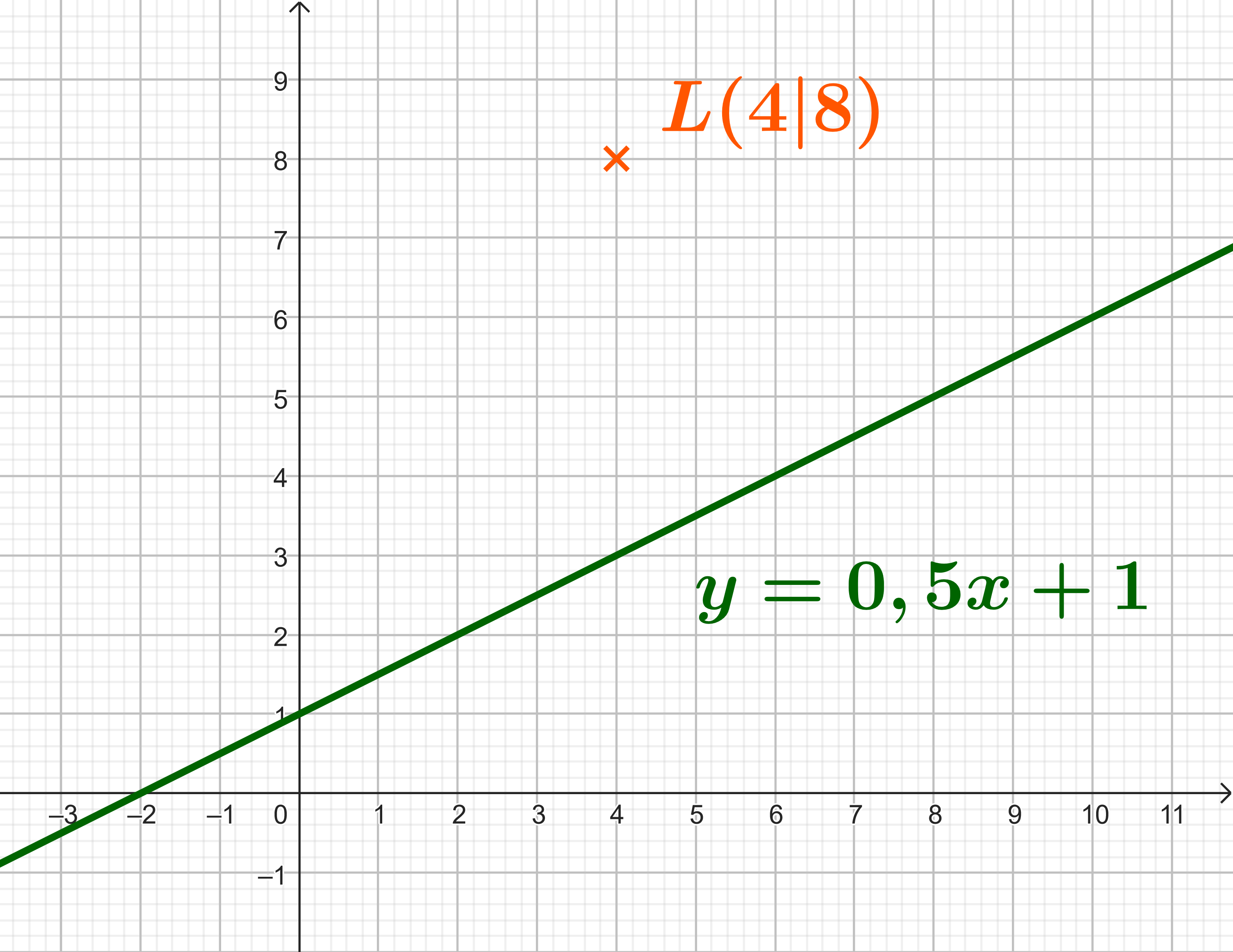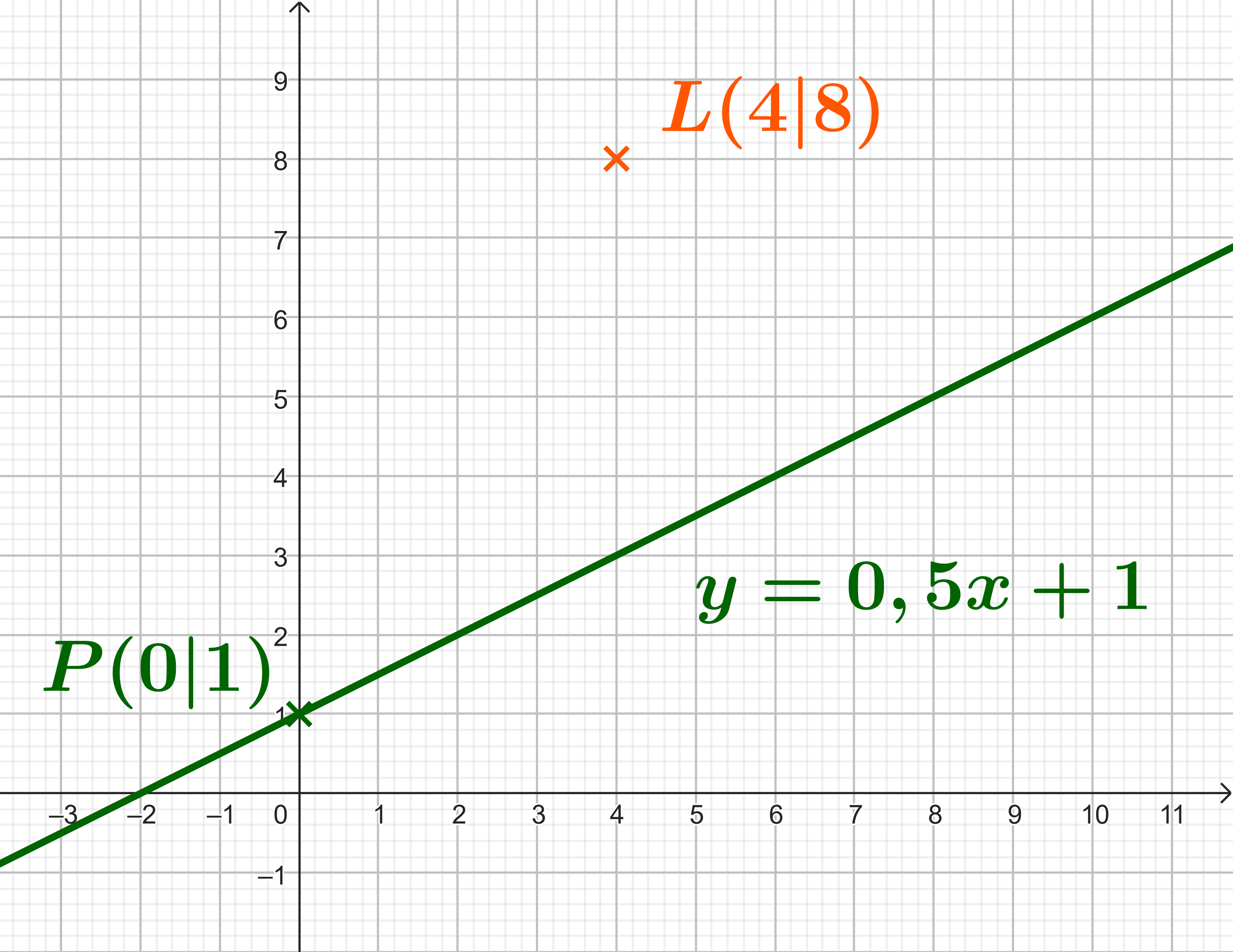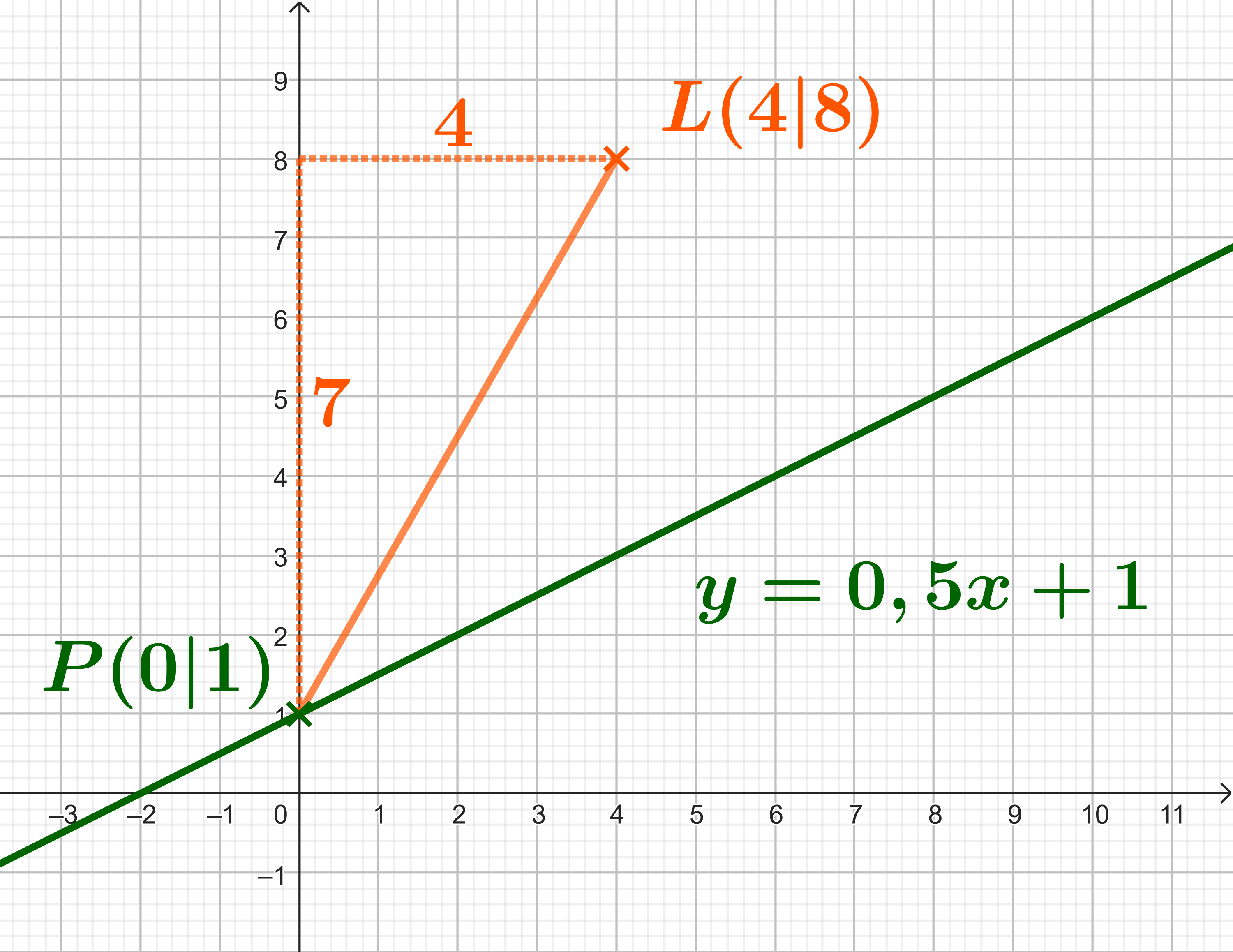Aufgaben zur Berechnung von Schnittpunkten von Geraden

Hier findest du Übungsaufgaben zur Bestimmung von Schnittpunkten von Geraden. Lerne, Schnittpunkte rechnerisch und graphisch zu bestimmen.

1
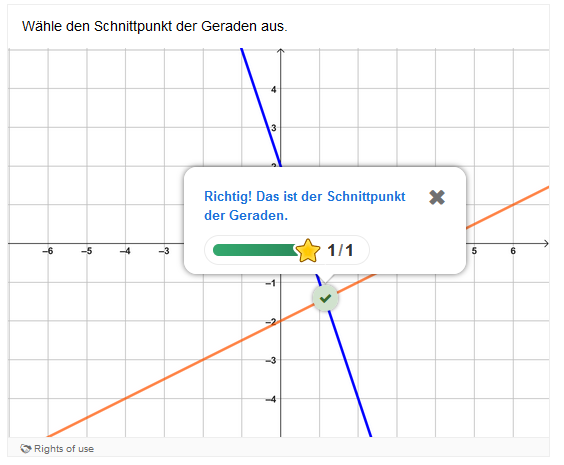
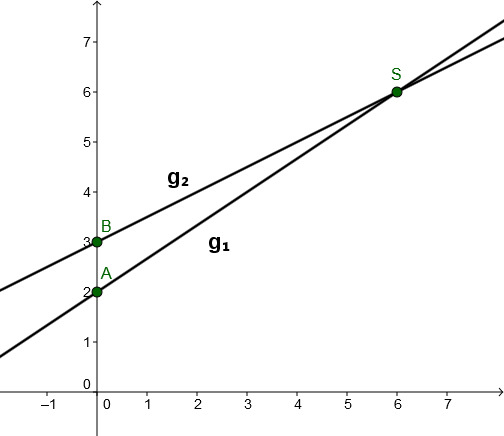
Finde den Schnittpunkt
1. Lösung der Aufgabe
  Lösung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Lösung der Aufgabe
  Lösung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
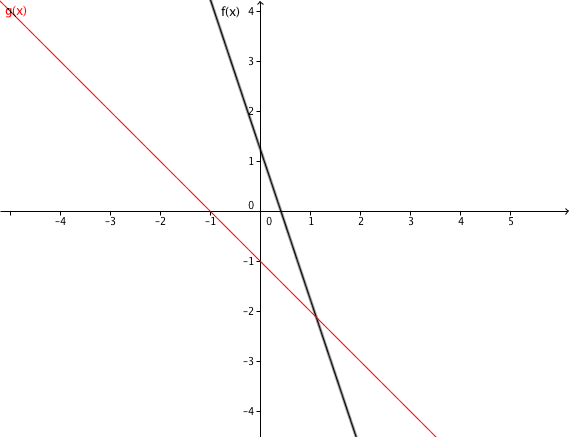
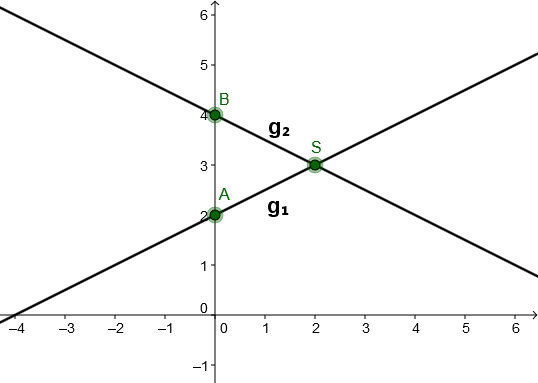
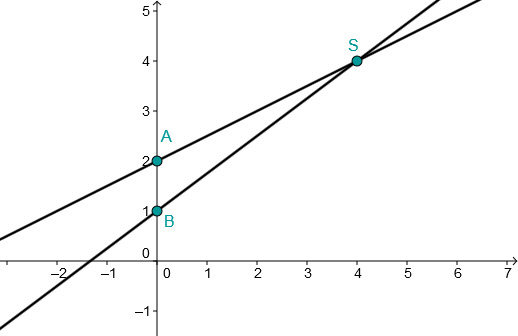
Bestimme den Schnittpunkt beider Geraden und zeichne diesen in ein Koordinatensystem.
Gib den Schnittpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
1. $f (x) = - 3 x + \frac{5}{4}; g (x) = - x - 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte linearer Funktionen
  Setze die Funktionen $f (x)$ und $g (x)$ gleich, um den Schnittpunkt zu bestimmen.
  $- 3 x + \frac{5}{4}$ $=$ $- x - 1$ $+ 3 x + 1$
  $- x + 3 x$ $=$ $\frac{5}{4} + 1$
  ↓
  Addiere
  $2 x$ $=$ $\frac{9}{4}$ $: 2$
  $x$ $=$ $\frac{9}{8} = 1,125$
  Setze $x$ in eine der beiden Geraden ein. Hier zum Beispiel $g :$
  $y$ $=$ $- \frac{9}{8} - 1$
  ↓
  Subtrahiere
  $y$ $=$ $- 2,125$
  $\Rightarrow S (1,125 / - 2,125)$
  Zeichnung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f : 2 y - x = 3; g (x) = - \frac{1}{2} x + 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte linearer Funktionen
  Setze die Funktionen f(x) und g(x) gleich, um den Schnittpunkt zu bestimmen.
  Löse zunächst die Funktion f nach y auf.
  $2 y - x$ $=$ $3$ $+ x$
  $2 y$ $=$ $3 + x$ $: 2$
  $y$ $=$ $\frac{3}{2} + \frac{x}{2}$
  Setze nun f und g gleich
  $\frac{3}{2} + \frac{x}{2}$ $=$ $- \frac{1}{2} x + 4$ $+ \frac{x}{2} - 1,5$
  $\frac{x}{2} + \frac{x}{2}$ $=$ $4 - 1,5$
  ↓
  Addiere und subtrahiere
  $x$ $=$ $2,5$
  Setze x in eine der beiden Geradengleichungen ein, hier zum Beispiel f:
  $y$ $=$ $\frac{3}{2} + \frac{2,5}{2}$
  ↓
  Addiere
  $y$ $=$ $2,75$
  $\Rightarrow S (2,5 / 2,75)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = - \frac{2}{3} x - 1; g (x) = \frac{1}{6} x - 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte linearer Funktionen
  Setze die Funktionen f(x) und g(x) gleich, um den Schnittpunkt zu bestimmen.
  $- \frac{2}{3} x - 1$ $=$ $\frac{1}{6} x - 4$ $+ \frac{2}{3} x + 4$
  $\frac{1}{6} x + \frac{2}{3} x$ $=$ $- 1 + 4$
  ↓
  Addiere.
  $\frac{5}{6} x$ $=$ $3$ $: \frac{5}{6}$
  $x$ $=$ $3 : \frac{5}{6}$
  ↓
  Dividiere durch einen Bruch $\to$ Multipliziere mit dem Kehrwert
  $x$ $=$ $3 \cdot \frac{6}{5}$
  ↓
  Multipliziere.
  $x$ $=$ $\frac{18}{5}$
  Setze x in eine der beiden Geraden ein, hier zum Beispiel g:
  $y$ $=$ $\frac{1}{6} \cdot \frac{18}{5} - 4$
  ↓
  Multipliziere.
  $y$ $=$ $\frac{3}{5} - 4$
  ↓
  Subtrahiere
  $y$ $=$ $- 3,4$
  $\Rightarrow S (3,6 / - 3,4)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f : x = 2; g (x) = - \frac{3}{4} x - \frac{3}{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte linearer Funktionen
  Setze $x = 2$ in $g (x)$ ein.
  $y$ $=$ $- \frac{3}{4} \cdot 2 - \frac{3}{2}$
  ↓
  Multipliziere.
  $y$ $=$ $- \frac{3}{2} - \frac{3}{2}$
  ↓
  Subtrahiere.
  $y$ $=$ $- \frac{6}{2}$
  ↓
  Dividiere.
  $y$ $=$ $- 3$
  $\Rightarrow S (2 / - 3)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
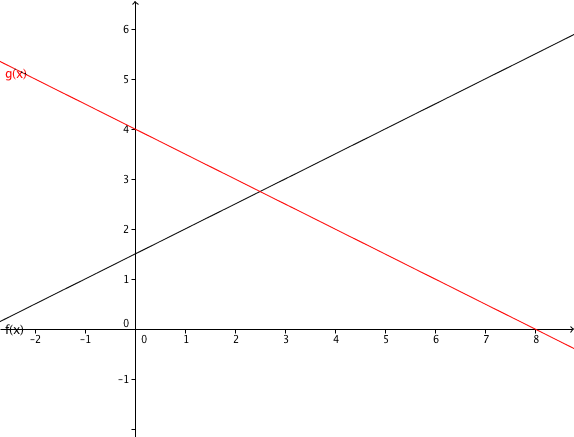
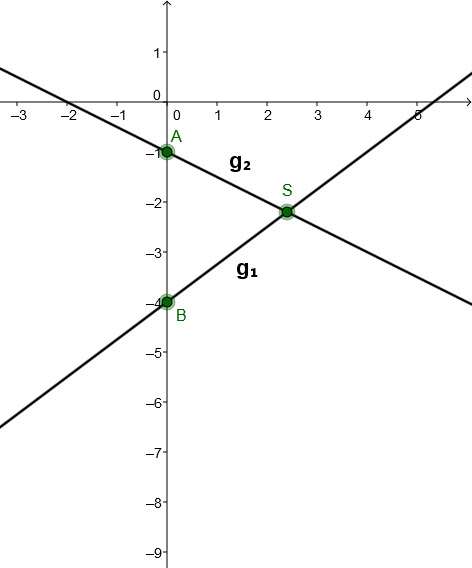
Bestimme den Schnittpunkt beider Geraden und zeichne die Graphen in ein Koordinatensystem.
Gib den Schnittpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
$f (x) = 0,05 x + 20; g (x) = 0,15 x + 15$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung des Schnittpunkts
Setze f(x) und g(x) gleich.
$0,05 x + 20$ $=$ $0,15 x + 15$ $- 0,05 x - 15$
$20 - 15$ $=$ $0,15 x - 0,05 x$
↓
Subtrahiere und vertausche die Seiten.
$0,10 x$ $=$ $5$ $: 0,1$
$x$ $=$ $\frac{5}{0,1}$
↓
Dividiere.
$x_{S}$ $=$ $50$
$x_{S} = 50$
Setze x in eine der beiden Funktionsgleichungen ein.
$y$ $=$ $0,05 \cdot 50 + 20$
↓
Multipliziere.
$y$ $=$ $2,5 + 20$
↓
Addiere.
$y_{S}$ $=$ $22,5$
$\Rightarrow S (x_{S}; y_{S}) = S (50; 22,5)$
$S$ ist der Schnittpunkt.
Zeichnung
Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt.

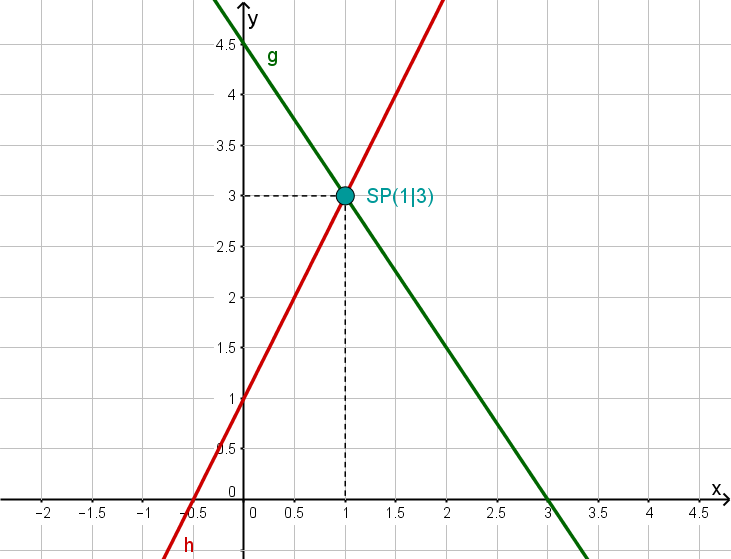
Geradenschnittpunkte berechnen.

Gegeben sind die Funktionsgleichungen zweier Geraden $g_{1} (x)$ und $g_{2} (x)$ . Berechnen Sie den Schnittpunkt beider Geraden und zeichnen Sie die Geraden in ein Koordinatensystem.

Gib den Schnittpunkt in das Eingabefeld ein: "S(1;3)" oder S(1|3)" zum Beispiel.

$g_{1} (x) = \frac{1}{2} x + 2 g_{2} (x) = - \frac{1}{2} x + 4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Geradenschnittpunkte berechnen
Setze dafür $g_{1} (x)$ und $g_{2} (x)$ gleich.
$\frac{1}{2} x + 2$ $=$ $- \frac{1}{2} x + 4$ $| + \frac{1}{2} x - 2$
$\frac{1}{2} x + \frac{1}{2} x$ $=$ $4 - 2$
$x_{S}$ $=$ $2$
↓
Setze x in $g_{1} (x)$ ein.
$y$ $=$ $1 + 2$
$y_{S}$ $=$ $3$
$\Rightarrow S (x_{S} | y_{S}) = S (2 | 3)$
Zeichnung
Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$g_{1} (x) = 2 x - 1 g_{2} (x) = - 2 x + 1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Geradenschnittpunkt berechnen
Setze $g_{1} (x)$ und $g_{2} (x)$ gleich.
$2 x - 1$ $=$ $- 2 x + 1$ $+ 2 x + 1$
$2 x + 2 x$ $=$ $1 + 1$
$4 x$ $=$ $2$ $: 4$
$x_{S}$ $=$ $\frac{1}{2}$
↓
Setze x in $g_{1} (x)$ ein.
$y$ $=$ $2 \cdot \frac{1}{2} - 1$
$y$ $=$ $1 - 1$
$y_{S}$ $=$ $0$
$\Rightarrow S (x_{S} | y_{S}) = S (\frac{1}{2} | 0)$
$\Rightarrow S$ ist der Schnittpunkt der Geraden.
Zeichnung
Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$g_{1} (x) = \frac{3}{4} x - 4 g_{2} (x) = - \frac{1}{2} x - 1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Geradenschnittpunkt berechnen
Setze $g_{1} (x)$ und $g_{2} (x)$ gleich.
$g_{1} (x)$ $=$ $g_{2} (x)$
$\frac{3}{4} x - 4$ $=$ $- \frac{1}{2} x - 1$ $+ \frac{1}{2} x + 4$
$\frac{3}{4} x + \frac{1}{2} x$ $=$ $- 1 + 4$
$1,25 x$ $=$ $3$ $1,25$
$x$ $=$ $\frac{3}{1,25}$
$x_{S}$ $=$ $2,4$
↓
Setze $x_{S}$ in $g_{1} (x)$ ein.
$y$ $=$ $\frac{3}{4} \cdot 2,4 - 4$
$y$ $=$ $1,8 - 4$
$y_{S}$ $=$ $- 2,2$
$\Rightarrow S (x_{S} | y_{S}) = S (2,4 | - 2,2)$
Zeichnung
Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$g_{1} (x) = - \frac{1}{2} x + 2 g_{2} (x) = \frac{1}{2} x + 3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Geradenschnittpunkt berechnen
Setze $g_{1} (x)$ und $g_{2} (x)$ gleich.
$g_{1} (x)$ $=$ $g_{2} (x)$
$- \frac{1}{2} x + 2$ $=$ $\frac{1}{2} x + 3$ $| + \frac{1}{2} x - 3$
$2 - 3$ $=$ $\frac{1}{2} x + \frac{1}{2} x$
$x_{S}$ $=$ $- 1$
↓
Setze $x_{S}$ in $g_{1} (x)$ ein.
$y$ $=$ $- \frac{1}{2} \cdot (- 1) + 2$
$y$ $=$ $\frac{1}{2} + 2$
$y_{S}$ $=$ $2,5$
$\Rightarrow S (x_{S} | y_{S}) = S (- 1 | 2,5)$
$\Rightarrow S$ ist der Schnittpunkt der Geraden.
Zeichnung
Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$g_{1} (x) = \frac{2}{3} x + 2 g_{2} (x) = \frac{1}{2} x + 3$

$g_{1} (x) = \frac{3}{4} x + 1 g_{2} (x) = \frac{1}{2} x + 2$

5
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
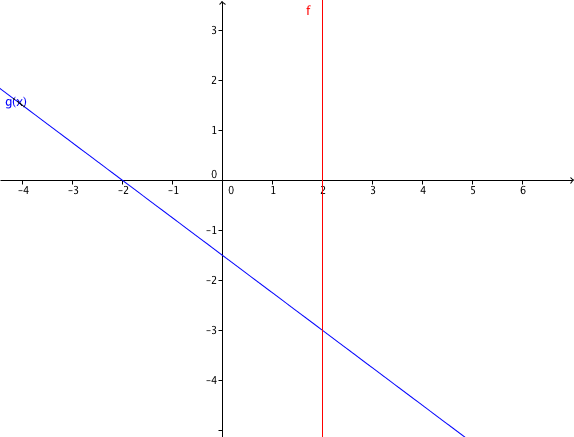
Betrachte folgende Graphen.
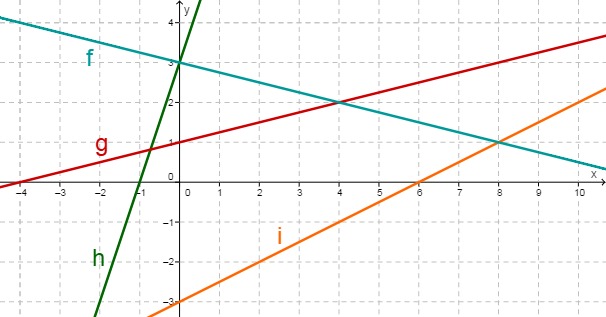
1. Bestimme die Funktionsgleichungen von allen 4 Geraden.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  $f (x) : y = m_{f} x + b_{f}$
  Um die Geradengleichung von f zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden f liegen. In diesem Fall ergibt sich zum Beispiel $A (0 | 3)$ und $B (4 | 2)$ . Bestimme mit diesen die Steigung von f mit der Formel.
  $m_{f} = \frac{y_{B} - y_{A}}{x_{B} - x_{A}}$
  Setz die Werte ein.
  $m_{f} = \frac{2 - 3}{4 - 0} = - \frac{1}{4}$
  Bestimme jetzt den y-Achsenabschnitt $b_{f}$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf f liegt, oder abliest, bei welchem Wert f die y-Achse schneidet.
  $f (x) : y = m_{f} x + b_{f}$
  Setz zum Beispiel $A$ ein.
  $3 = - \frac{1}{4} \cdot 0 + b_{f}$
  Vereinfache.
  $3 = b_{f} \Rightarrow b_{f} = 3$
  Also lautet die Geradengleichung $f (x) = - \frac{1}{4} \cdot x + 3$ .
  $g (x) : y = m_{g} x + b_{g}$
  Um die Geradengleichung von g zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden g liegen. In diesem Fall ergibt sich zum Beispiel $C (- 4 | 0)$ und $D (0 | 1)$ . Bestimme mit diesen die Steigung von g mit der Formel.
  $m_{g} = \frac{y_{D} - y_{C}}{x_{D} - x_{C}}$
  Setz die Werte ein.
  $m_{g} = \frac{1 - 0}{0 - (- 4)} = \frac{1}{4}$
  Bestimme jetzt den y-Achsenabschnitt $b_{g}$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf g liegt, oder abliest, bei welchem Wert g die y-Achse schneidet.
  $g (x) : y = m_{g} x + b_{g}$
  Setz zum Beispiel $D$ ein.
  $1 = \frac{1}{4} \cdot 0 + b_{g}$
  Vereinfache.
  $1 = b_{g} \Rightarrow b_{g} = 1$
  Also lautet die Geradengleichung $g (x) = \frac{1}{4} \cdot x + 1$ .
  $h (x) : y = m_{h} x + b_{h}$
  Um die Geradengleichung von h zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden h liegen. In diesem Fall ergibt sich zum Beispiel $E (- 1 | 0)$ und $A (0 | 3)$ . Bestimme mit diesen die Steigung von h mit der Formel.
  $m_{h} = \frac{y_{A} - y_{E}}{x_{A} - x_{E}}$
  Setz die Werte ein.
  $m_{h} = \frac{3 - 0}{0 - (- 1)} = 3$
  Bestimme jetzt den y-Achsenabschnitt $b_{h}$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf h liegt, oder abliest, bei welchem Wert h die y-Achse schneidet.
  $h (x) : y = m_{h} x + b_{h}$
  Setz zum Beispiel $A$ ein.
  $3 = 3 \cdot 0 + b_{h}$
  Vereinfache.
  $3 = b_{h} \Rightarrow b_{h} = 3$
  Also lautet die Geradengleichung $h (x) = 3 \cdot x + 3$ .
  $i (x) : y = m_{i} x + b_{i}$
  Um die Geradengleichung von i zu bestimmen, liest du zuerst zwei Punkte aus dem Diagramm ab, die auf der Geraden i liegen. In diesem Fall ergibt sich zum Beispiel $F (0 | - 3)$ und $S (6 | 0)$ . Bestimme mit diesen die Steigung von i mit der Formel.
  $m_{i} = \frac{y_{S} - y_{F}}{x_{S} - x_{F}}$
  Setz die Werte ein.
  $m_{i} = \frac{0 - (- 3)}{6 - 0} = \frac{1}{2}$
  Bestimme jetzt den y-Achsenabschnitt $b_{i}$ , indem du einen Punkt in die allgemeine Geradengleichung einsetzt, der auf i liegt, oder abliest, bei welchem Wert i die y-Achse schneidet.
  $i (x) : y = m_{i} x + b_{i}$
  Setz zum Beispiel $F$ ein.
  $- 3 = \frac{1}{2} \cdot 0 + b_{i}$
  Vereinfache.
  $- 3 = b_{i} \Rightarrow b_{i} = - 3$
  Also lautet die Geradengleichung $i (x) = \frac{1}{2} \cdot x - 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme den Schnittpunkt von g und h , sowie die Nullstelle von f.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
  Schnittpunkt $P (x_{p} | y_{p})$ von g und h
  Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach $x$ um. Die Funktionsgleichungen lauten (Teilaufgabe a) $g (x) : y = \frac{1}{4} x + 1$ und $h (x) : y = 3 x + 3$ .
  $\frac{1}{4} x_{P} + 1$ $=$ $3 x_{P} + 3$ $- 3 x_{p} - 1$
  ↓
  Subtrahiere $3 x_{P}$ und 1.
  $- \frac{11}{4} x_{P}$ $=$ $2$ $\div (- \frac{11}{4})$
  ↓
  Dividiere durch $- \frac{11}{4}$ .
  $x_{p}$ $=$ $- \frac{8}{11}$
  Setz nun $- \frac{8}{11}$ in die Geradengleichung von g oder h ein, um $y_{P}$ zu bestimmen.
  $h (x_{P}) : y_{P} = 3 \cdot x_{P} + 3$
  Setz $x_{P}$ ein.
  $y_{P} = 3 \cdot (- \frac{8}{11}) + 3 = \frac{9}{11}$
  Die Geraden g und h schneiden sich also bei $P (- \frac{8}{11} | \frac{9}{11})$ .
  Die Nullstelle $x_{N_{f}}$ von f bestimmst du, indem du die Funktionsgleichung $f (x) : y = - \frac{1}{4} x + 3$ mit 0 gleichsetzt und nach $x$ umformst.
  $- \frac{1}{4} x_{N_{f}} + 3$ $=$ $0$ $- 3$
  $- \frac{1}{4} x_{N_{f}}$ $=$ $- 3$ $: \frac{1}{4}$
  $x_{N_{f}}$ $=$ $12$
  Die Nullstelle von f ist also 12.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Berechne die beiden Schnittpunkte, die außerhalbdes Bildbereichs liegen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
  Der Schnittpunkt von h und i und der Schnittpunkt von g und i liegen außerhalb des Bildbereichs.
  Schnittpunkt $T (x_{T} | y_{T})$ von h und i
  Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach $x$ um. Die Funktionsgleichungen lauten (Teilaufgabe a) $h (x) : y = 3 x + 3$ und $i (x) : y = \frac{1}{2} x - 3$ .
  $3 x_{T} + 3$ $=$ $\frac{1}{2} x_{T} - 3$ $- \frac{1}{2} x - 3$
  $\frac{5}{2} x_{T}$ $=$ $- 6$ $: \frac{5}{2}$
  $x_{T}$ $=$ $- \frac{12}{5}$
  Setz nun $- \frac{12}{5}$ in die Geradengleichung von h oder i ein, um $y_{T}$ zu bestimmen.
  $h (x_{T}) : y_{T} = 3 \cdot x_{T} + 3$
  Setz $x_{T}$ ein.
  $y_{T} = 3 \cdot (- \frac{12}{5}) + 3 = - \frac{21}{5}$
  Die Geraden h und i schneiden sich also bei $T (- \frac{12}{5} | - \frac{21}{5})$ .
  Schnittpunkt $Q (x_{Q} | y_{Q})$ von g und i
  Um den Schnittpunkt von zwei Funktionen zu bestimmen, setzt du diese gleich und formst nach $x$ um. Die Funktionsgleichungen lauten (Teilaufgabe a) $g (x) : y = \frac{1}{4} x + 1$ und $i (x) : y = \frac{1}{2} x - 3$ .
  $\frac{1}{4} x_{Q} + 1$ $=$ $\frac{1}{2} x_{Q} - 3$ $- \frac{1}{2} x - 1$
  $- \frac{1}{4} x_{Q}$ $=$ $- 4$ $: (- \frac{1}{4})$
  $x_{Q} = 16$
  Setz nun $16$ in die Geradengleichung von g oder i ein, um $y_{Q}$ zu bestimmen.
  $g (x_{Q}) : y_{Q} = \frac{1}{4} \cdot x_{Q} + 1$
  Setz $x_{Q}$ ein.
  $y_{Q} = \frac{1}{4} \cdot 16 + 1 = 5$
  Die Geraden g und i schneiden sich also bei $Q (16 | 5)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Wie viele Schnittpunkte gibt es höchstens bei vier Geraden, die jeweils nicht parallel sind?
  Schnittpunkte kann es höchstens geben.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
  Es gibt insgesamt 6 Schnittpunkte, nämlich die folgenden:
  f und g
  f und h
  f und i
  g und h
  g und i
  h und i
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Berechne den Schnittpunkt der Geradenpaare.

Gib den Schnittpunkt in das Eingabefeld ein, zum Beispiel so: "S(4|-5)" oder "S(4;-5)"

Wenn es keinen Schnittpunkt gibt, gib "-" ein.

$y = 3 x + 4$ und $y = - 2 x + 14$

$y = 6 x - 3$ und $y = 7 x - 11$

$y = 8 x + 3$ und $y = - 4 x + 6$

$y = 7 x - 14$ und $y = 7 x - 3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen berechnen
Geraden mit gleicher Steigung (hier 7) schneiden sich nicht, denn sie sind parallel zueinander.Setzt man die Funktionsterme gleich, so erhält man eine falsche Aussage, also keinen Schnittpunkt.
$7 x - 14$ $=$ $7 x - 3$ $- 7 x$
$- 14$ $=$ $- 3$
↓
falsche Aussage!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$y = \frac{1}{6} x - 4$ und $y = \frac{1}{3} x - 10$

$y = \frac{1}{2} x + \frac{3}{2}$ und $y = \frac{1}{2}$

7
Zeige rechnerisch, dass sich die drei Geraden $g_{1}$ : $y = 0,5 x$ ; $g_{2}$ : $y = x - 1,5$ ; $g_{3}$ : $y = - 2 x + 7,5$ in genau einem Punkt schneiden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Geraden
Schnittpunkt zweier Geraden
$g_{2}$ : $y = x - 1,5$ ; $g_{3} :$ $y = - 2 x + 7,5$
Es ist hier zu empfehlen, zunächst den Schnittpunkt von zwei Geraden zu berechnen und dann zu prüfen, ob der Schnittpunkt auch ein Punkt auf der anderen Gerade ist.
Zwei der drei Geraden werden gleichgesetzt, um die x-Koordinate des Schnittpunktes zu berechnen.
$x - 1,5$ $=$ $- 2 x + 7,5$
↓
Addiere zunächst 2x und anschließend 1,5.
$3 x$ $=$ $9$
↓
Dividiere durch 3.
$x$ $=$ $3$
Den x-Wert in eine der beiden gleichgesetzten Geraden einsetzen (z. B. $g_{2}$ ), um die y-Koordinate des Schnittpunktes von $g_{2}$ und $g_{3}$ zu berechnen.
$y = 3 - 1,5 = 1,5$
$\Rightarrow$ $S (3 | 1,5)$
Gerade überprüfen
$g_{1}$ : $y = 0,5 x$
Der Schnittpunkt wird nun in $g_{1}$ eingesetzt. Das heißt, dass $x$ und $y$ der Gerade $g_{1}$ durch 3 und 1,5 ersetzt werden.
$1,5 = 0,5 \cdot 3$
Prüfe ob die so entstandene Aussage wahr ist, um festzustellen, ob $g_{1}$ durch $S$ läuft.
$1,5 = 1,5$
$\Rightarrow$ Dies ist eine wahre Aussage, also ist $S$ der gemeinsame und einzige Schnittpunkt aller drei Geraden.
8
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Prüfe, ob die Geraden $g, h, i$ durch einen Punkt verlaufen.
1. $g (x) = x + 1; h : 2 y + x + 4 = 0; i : 3 y - 5 x = 7$
  Ja sie verlaufen durch einen Punkt.
  Nein, sie verlaufen nicht durch einen Punkt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt von Geraden
  Bringe zuerst alle Geraden in die allgeimeine Form $y = m x + t$ .
  Gerade g:
  $g (x) = x + 1$
  $\Leftrightarrow y = x + 1$
  Gerade h:
  $2 y + x + 4 = 0$
  $\Leftrightarrow 2 y = - x - 4$
  $\Leftrightarrow y = - \frac{1}{2} x - 2$
  Gerade i:
  $3 y - 5 x = 7$
  $\Leftrightarrow 3 y = 5 x + 7$
  $\Leftrightarrow y = \frac{5}{3} x + \frac{7}{3}$
  Bestimme den Schnittpunkt von g und h
  Setze dazu die jeweiligen rechten Seiten gleich.
  $x + 1$ $=$ $- \frac{1}{2} x - 2$ $+ \frac{1}{2} x - 1$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $x + \frac{1}{2} x$ $=$ $- 2 - 1$
  ↓
  Fasse zusammen.
  $\frac{3}{2} x$ $=$ $- 3$ $: \frac{3}{2}$
  $x$ $=$ $- 2$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = - 2 + 1 = - 1$
  Der Schnittpunkt ist $S_{g h} (- 2 | - 1) .$
  Bestimme den Schnittpunkt von g und i
  Setze dazu die jeweiligen rechten Seiten gleich.
  $x + 1$ $=$ $\frac{5}{3} x + \frac{7}{3}$ $- \frac{5}{3} x - 1$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $x - \frac{5}{3} x$ $=$ $\frac{7}{3} - 1$
  ↓
  Fasse zusammen.
  $- \frac{2}{3} x$ $=$ $\frac{4}{3}$ $: (- \frac{2}{3})$
  $x$ $=$ $- 2$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = - 2 + 1 = - 1$
  Der Schnittpunkt ist $S_{g i} (- 2 | - 1) .$
  Da sich $g$ mit $h$ und mit $i$ im selben Punkt schneidet, schneiden sich auch $h$ und $i$ in diesem Punkt. Die Geraden laufen also alle durch den Punkt $(- 2 | - 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $g (x) = \frac{1}{6} x + \frac{3}{2}; h (x) = - \frac{2}{3} x + 2; i : 2 x - y = 3$
  Ja sie verlaufen durch einen Punkt.
  Nein, sie verlaufen nicht durch einen Punkt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt von Geraden
  Bringe zuerst alle Geraden in die allgeimeine Form $y = m x + t$ .
  Gerade g:
  $g (x) = \frac{1}{6} x + \frac{3}{2}$
  $\Leftrightarrow y = \frac{1}{6} x + \frac{3}{2}$
  Gerade h:
  $h (x) = - \frac{2}{3} x + 2$
  $\Leftrightarrow y = - \frac{2}{3} x + 2$
  Gerade i:
  $2 x - y = 3$
  $\Leftrightarrow y = 2 x - 3$
  Bestimme den Schnittpunkt von g und h
  Setze dazu die jeweiligen rechten Seiten gleich.
  $\frac{1}{6} x + \frac{3}{2}$ $=$ $- \frac{2}{3} x + 2$ $+ \frac{2}{3} x - \frac{3}{2}$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $\frac{1}{6} x + \frac{2}{3} x$ $=$ $2 - \frac{3}{2}$
  ↓
  Fasse zusammen.
  $\frac{5}{6} x$ $=$ $\frac{1}{2}$ $: \frac{5}{6}$
  $x$ $=$ $\frac{3}{5}$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = \frac{1}{6} \cdot \frac{3}{5} + \frac{3}{2}$
  $= \frac{1}{10} + \frac{3}{2} = \frac{16}{10}$
  $= \frac{8}{5}$
  Der Schnittpunkt ist $S_{g h} (\frac{3}{5} | \frac{8}{5}) .$
  Bestimme den Schnittpunkt von g und i
  Setze dazu die jeweiligen rechten Seiten gleich.
  $\frac{1}{6} x + \frac{3}{2}$ $=$ $2 x - 3$ $- 2 x - \frac{3}{2}$
  ↓
  Sortiere nach $x$ -Termen und Zahlen.
  $\frac{1}{6} x - 2 x$ $=$ $- 3 - \frac{3}{2}$
  ↓
  Fasse zusammen.
  $- \frac{11}{6} x$ $=$ $- \frac{9}{2}$ $: (- \frac{11}{6})$
  $x$ $=$ $\frac{9}{2} \cdot \frac{6}{11} = \frac{27}{11}$
  Setze in $g$ ein, um den Schnittpunkt zu erhalten.
  $y = \frac{1}{6} \cdot \frac{27}{11} + \frac{3}{2}$
  $= \frac{9}{22} + \frac{3}{2} = \frac{42}{22}$
  $= \frac{21}{11}$
  Der Schnittpunkt ist $S_{g i} (\frac{27}{11} | \frac{21}{11}) .$
  Damit schneidet die Gerade $g$ die Gerade $h$ in einem anderen Punkt als die Gerade $i$ . Also laufen die Geraden nicht durch einen Punkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
Bestimmung von Schnittpunkten
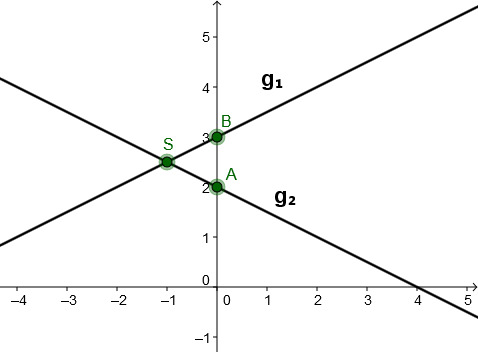
Gegeben ist eine Gerade g und eine Gerade h.
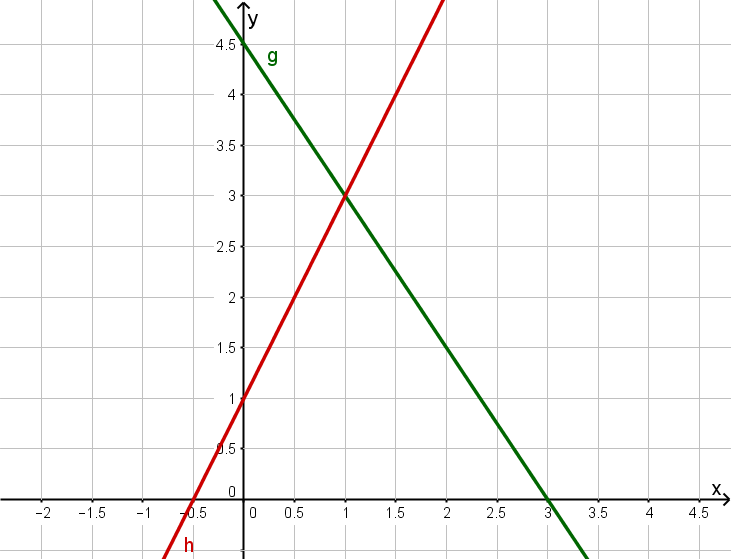
1. Bestimme die Geradengleichungen von g und h.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  $y = m x + t$
  Der Parameter $m$ ist die Steigung der Geraden. Der Parameter $t$ ist der y-Achsenabschnitt.
  Gerade g:
  $y = m_{g} x + t_{g}$
  Die Gerade g hat die Steigung $- \frac{3}{2}$ , das heißt $m_{g} = - \frac{3}{2}$ .
  $y = - \frac{3}{2} x + t_{g}$
  Sie schneidet die y-Achse bei $\frac{9}{2}$ , das heißt $t_{g} = \frac{9}{2}$ .
  $y = - \frac{3}{2} x + \frac{9}{2}$
  Gerade h:
  $y = m_{h} x + t_{h}$
  Die Gerade h hat die Steigung $2$ , das heißt $m_{h} = 2$
  $y = 2 x + t_{h}$
  Die Gerade schneidet die y-Achse bei $1$ , das heißt $t_{h} = 1$ .
  $y = 2 x + 1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
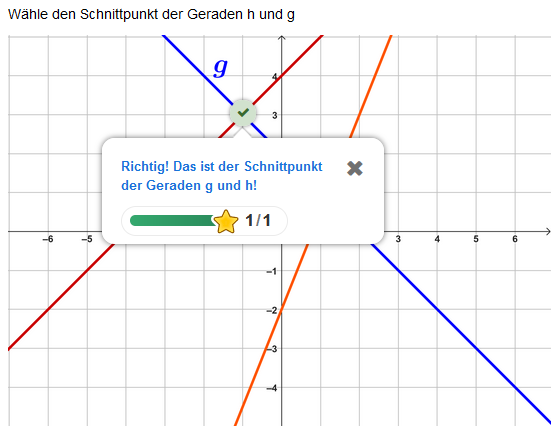
2. Lies den Schnittpunkt ab.
  Gib den Punkt in das Eingabefeld ein. Beispiel: "(-2;1)" oder "(-2|1)"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt
  Schnittpunkte ablesen
  Wir lesen aus der Zeichnung den Schnittpunkt $SP (1 | 3)$ ab.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
Der Leuchtturm
Ein Leuchtturm befindet sich im Punkt $L (4 | 8)$ . Mit deinem Schiff befindest du dich auf dem Kurs $y = 0,5 x + 1$ .
Runde alle Ergebnisse auf zwei Stellen nach dem Komma. Es gibt verschiedene Lösungswege.
1. Welchen Abstand hat dein Schiff zum Leuchtturm, wenn es sich bei $x = 0$ befindet.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
  Berechnung des Abstands an der Stelle $x = 0$ .
  Grundsätzlich ist eine Skizze des Problems immer hilfreich. Es kann einerseits zu einer graphsichen Lösung führen oder auch den Ansatz zu einer rechnerischen Lösung veranschaulichen.
  An der Stelle $x = 0$ befindet sich das Schiff im Punkt $P (0 | 1)$ .
  Der Abstand zwischen Schiff und Leuchtturm ist die Länge der Strecke $P L$ .
  In der Skizze lässt sich ein rechtwinkliges Dreieck finden, sodass der Abstand mit dem Satz des Pythagoras berechnet werden kann:
  $| P L | = \sqrt{7^{2} + 4^{2}} = \sqrt{65} \approx 8,06$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere ein Koordinatensystem, zusammen mit dem Punkt $L (4 | 8)$ und die Route des Schiffes.
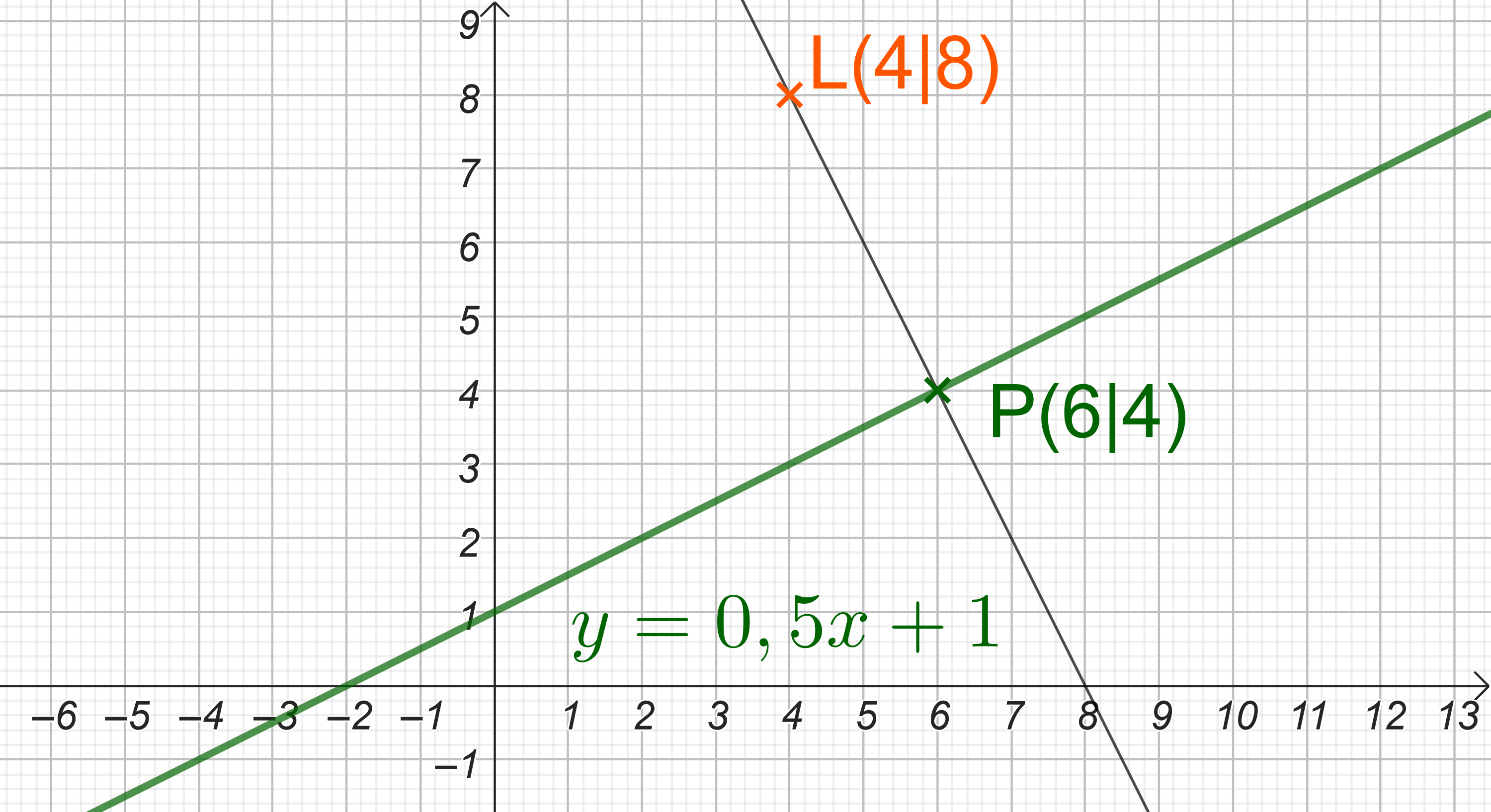
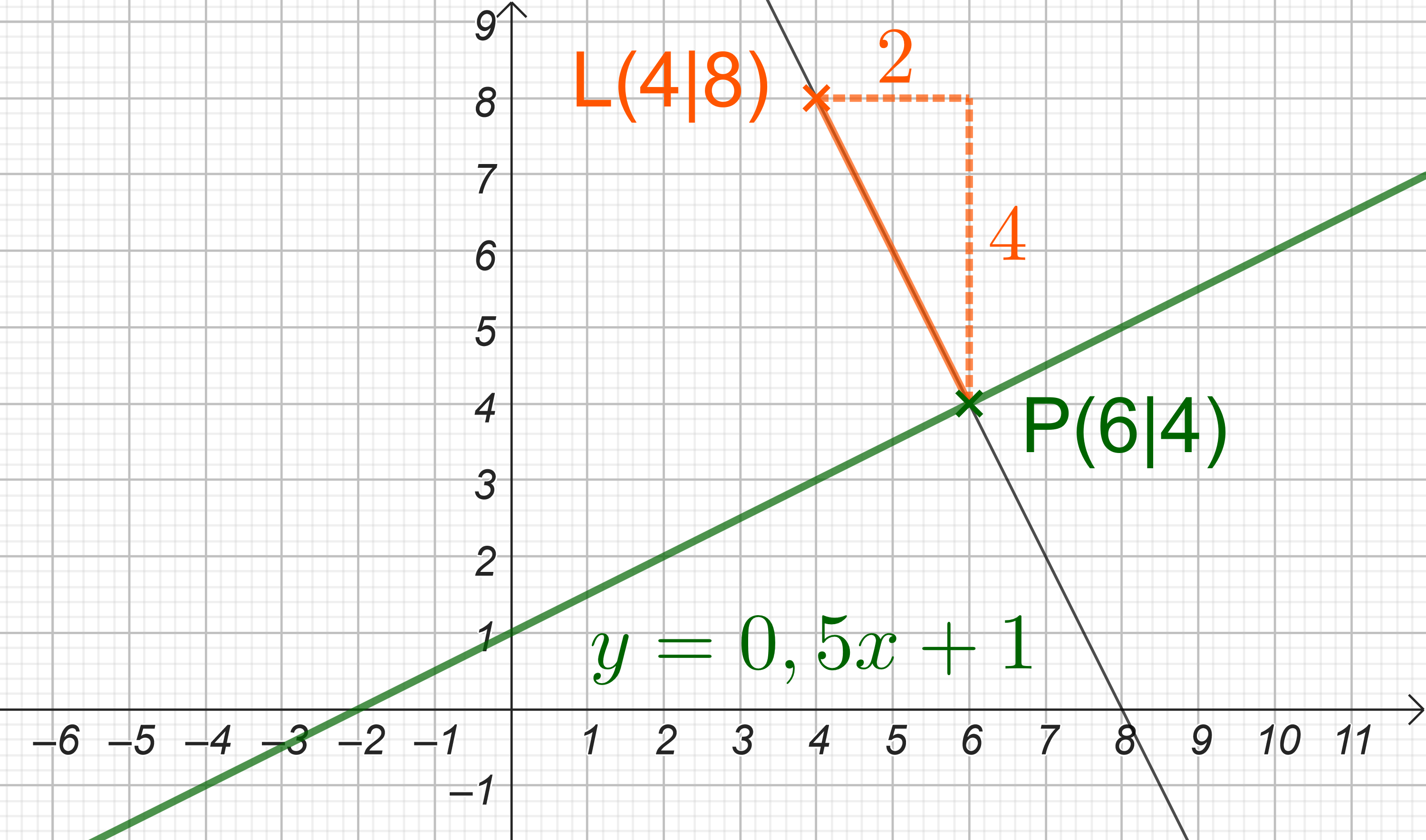
2. Das Schiff fährt auf besagter Route $y = 0,5 x + 1$ . Bei welchen Koordinaten hat es den kürzesten Abstand zum Leuchtturm? Gib den Punkt in der Form $(x, y)$ an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lotgerade
  Graphische Lösung
  Die kürzeste Strecke zwischen Schiff und Leuchtturm gibt es dann, wenn die Verbindungslinie senkrecht zur Schiffsroute steht. Man spricht von der Lotgeraden.
  Wenn man die Verbindungslinie senkrecht zur Schiffsroute einzeichnet, ergibt sich der Punkt $P (6 | 4)$ . Dort muss sich das Schiff befinden, damit es den kürzesten Abstand zum Leuchtturm hat.
  Modellieren der Lotgeraden
  Gesucht ist eine Gerade, die senkrecht zur Schiffsroute $y = 0,5 x + 1$ ist. Diese muss die Steigung $m = - 2$ haben. Zudem muss die Gerade durch den Punkt $L (4 | 8)$ verlaufen.
  Der Ansatz für diese Gerade lautet:
  $y_{Lot} = - 2 x + b$
  $y_{L o t}$ $=$ $- 2 x + b$
  ↓
  Einsetzen von $L (4 | 8)$
  $8$ $=$ $- 2 \cdot 4 + b$
  $8$ $=$ $- 8 + b$ $+ 8$
  $16$ $=$ $b$
  Die Lotgerade ist damit $y_{Lot} = - 2 x + 16$ .
  x-Koordinate des Schnittpunkts
  Die gesuchten Koordinaten sind der Schnittpunkt der beiden Geraden:
  $y$ $=$ $y_{L o t}$
  $0,5 x + 1$ $=$ $- 2 x + 16$ $- 16$
  $0,5 x - 15$ $=$ $- 2 x$ $- 0,5 x$
  $- 15$ $=$ $- 2,5 x$ $\cdot (- 1)$
  $15$ $=$ $2,5 x$ $: 2,5$
  $6$ $=$ $x$
  y-Koordinate des Schnittpunkts
  Die y-Koordinate kann mit beiden Geraden bestimmt werden. Mit der Schiffsroute zum Beispiel:
  $y = 0,5 \cdot 6 + 1 = 3 + 1 = 4$
  Der Schnittpunkt ist also $P (6 | 4)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es gibt eine einfache, graphische Lösung und eine aufwändigere, rechnerische Lösung. Für die rechnerische Lösung muss eine Gerade für das Lot modelliert werden.
3. Gib den kürzesten Abstand zwischen Schiff und Leuchtturm an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
  Kürzester Abstand zwischen Schiff und Leuchtturm
  Wie in Teilaufgabe (a) kann der Abstand zwischen den Punkten mit dem Satz des Pythagoras berechnet werden:
  $| P L | = \sqrt{2^{2} + 4^{2}} = \sqrt{20} \approx 4,47$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Abstand zwischen den Punkten $L (4 | 8)$ (Leuchtturm) und $P (6 | 4)$ (Schiff).
11
Schnittpunkte zweier Geraden berechnen
Bestimme den Schnittpunkt der Geraden $g : y = 2 x + 3$ und $h : y = - x + 6$
$S (1, 5)$
$S (2, 7)$
$S (1, 3)$
$S (2, 5)$
Setze die Gleichungen gleich, um den x-Wert des Schnittpunktes zu berechnen: $2 x + 3 = - x + 6$ .
Addiere $x$ auf beiden Seiten der Gleichung, um alle x-Terme auf einer Seite zu haben: $3 x + 3 = 6$ .
Subtrahiere 3 auf beiden Seiten, um $x$ zu isolieren: $3 x = 3$ .
Teile beide Seiten durch 3, um den Wert von $x$ zu erhalten: $x = 1$ .
Setze den Wert von $x$ in eine der beiden Gleichungen ein, um $y$ zu berechnen. Wir verwenden die erste Gleichung: $y = 2 \cdot 1 + 3$ .
Berechne den Wert von $y$ : $y = 2 + 3 = 5$ .
Der Schnittpunkt $S$ hat die Koordinaten $(1; 5)$ .
Setze die Gleichungen gleich, um den x-Wert zu finden. Löse dann nach x auf und setze diesen Wert in eine der Gleichungen ein, um y zu berechnen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$- 3 x + \frac{5}{4}$	$=$	$- x - 1$	$+ 3 x + 1$
$- x + 3 x$	$=$	$\frac{5}{4} + 1$
	↓	Addiere
$2 x$	$=$	$\frac{9}{4}$	$: 2$
$x$	$=$	$\frac{9}{8} = 1,125$

$2 y - x$	$=$	$3$	$+ x$
$2 y$	$=$	$3 + x$	$: 2$
$y$	$=$	$\frac{3}{2} + \frac{x}{2}$

$\frac{3}{2} + \frac{x}{2}$	$=$	$- \frac{1}{2} x + 4$	$+ \frac{x}{2} - 1,5$
$\frac{x}{2} + \frac{x}{2}$	$=$	$4 - 1,5$
	↓	Addiere und subtrahiere
$x$	$=$	$2,5$

$- \frac{2}{3} x - 1$	$=$	$\frac{1}{6} x - 4$	$+ \frac{2}{3} x + 4$
$\frac{1}{6} x + \frac{2}{3} x$	$=$	$- 1 + 4$
	↓	Addiere.
$\frac{5}{6} x$	$=$	$3$	$: \frac{5}{6}$
$x$	$=$	$3 : \frac{5}{6}$
	↓	Dividiere durch einen Bruch $\to$ Multipliziere mit dem Kehrwert
$x$	$=$	$3 \cdot \frac{6}{5}$
	↓	Multipliziere.
$x$	$=$	$\frac{18}{5}$

$y$	$=$	$\frac{1}{6} \cdot \frac{18}{5} - 4$
	↓	Multipliziere.
$y$	$=$	$\frac{3}{5} - 4$
	↓	Subtrahiere
$y$	$=$	$- 3,4$

$y$	$=$	$- \frac{3}{4} \cdot 2 - \frac{3}{2}$
	↓	Multipliziere.
$y$	$=$	$- \frac{3}{2} - \frac{3}{2}$
	↓	Subtrahiere.
$y$	$=$	$- \frac{6}{2}$
	↓	Dividiere.
$y$	$=$	$- 3$

$0,05 x + 20$	$=$	$0,15 x + 15$	$- 0,05 x - 15$
$20 - 15$	$=$	$0,15 x - 0,05 x$
	↓	Subtrahiere und vertausche die Seiten.
$0,10 x$	$=$	$5$	$: 0,1$
$x$	$=$	$\frac{5}{0,1}$
	↓	Dividiere.
$x_{S}$	$=$	$50$

$y$	$=$	$0,05 \cdot 50 + 20$
	↓	Multipliziere.
$y$	$=$	$2,5 + 20$
	↓	Addiere.
$y_{S}$	$=$	$22,5$

$\frac{1}{2} x + 2$	$=$	$- \frac{1}{2} x + 4$	$\| + \frac{1}{2} x - 2$
$\frac{1}{2} x + \frac{1}{2} x$	$=$	$4 - 2$
$x_{S}$	$=$	$2$
	↓	Setze x in $g_{1} (x)$ ein.
$y$	$=$	$1 + 2$
$y_{S}$	$=$	$3$

$2 x - 1$	$=$	$- 2 x + 1$	$+ 2 x + 1$
$2 x + 2 x$	$=$	$1 + 1$
$4 x$	$=$	$2$	$: 4$
$x_{S}$	$=$	$\frac{1}{2}$
	↓	Setze x in $g_{1} (x)$ ein.
$y$	$=$	$2 \cdot \frac{1}{2} - 1$
$y$	$=$	$1 - 1$
$y_{S}$	$=$	$0$

$\frac{1}{4} x_{P} + 1$	$=$	$3 x_{P} + 3$	$- 3 x_{p} - 1$
	↓	Subtrahiere $3 x_{P}$ und 1.
$- \frac{11}{4} x_{P}$	$=$	$2$	$\div (- \frac{11}{4})$
	↓	Dividiere durch $- \frac{11}{4}$ .
$x_{p}$	$=$	$- \frac{8}{11}$

$- \frac{1}{4} x_{N_{f}} + 3$	$=$	$0$	$- 3$
$- \frac{1}{4} x_{N_{f}}$	$=$	$- 3$	$: \frac{1}{4}$
$x_{N_{f}}$	$=$	$12$

$3 x_{T} + 3$	$=$	$\frac{1}{2} x_{T} - 3$	$- \frac{1}{2} x - 3$
$\frac{5}{2} x_{T}$	$=$	$- 6$	$: \frac{5}{2}$
$x_{T}$	$=$	$- \frac{12}{5}$

$\frac{1}{4} x_{Q} + 1$	$=$	$\frac{1}{2} x_{Q} - 3$	$- \frac{1}{2} x - 1$
$- \frac{1}{4} x_{Q}$	$=$	$- 4$	$: (- \frac{1}{4})$

$g_{1} (x)$	$=$	$g_{2} (x)$
$\frac{3}{4} x - 4$	$=$	$- \frac{1}{2} x - 1$	$+ \frac{1}{2} x + 4$
$\frac{3}{4} x + \frac{1}{2} x$	$=$	$- 1 + 4$
$1,25 x$	$=$	$3$	$1,25$
$x$	$=$	$\frac{3}{1,25}$
$x_{S}$	$=$	$2,4$
	↓	Setze $x_{S}$ in $g_{1} (x)$ ein.
$y$	$=$	$\frac{3}{4} \cdot 2,4 - 4$
$y$	$=$	$1,8 - 4$
$y_{S}$	$=$	$- 2,2$

$g_{1} (x)$	$=$	$g_{2} (x)$
$- \frac{1}{2} x + 2$	$=$	$\frac{1}{2} x + 3$	$\| + \frac{1}{2} x - 3$
$2 - 3$	$=$	$\frac{1}{2} x + \frac{1}{2} x$
$x_{S}$	$=$	$- 1$
	↓	Setze $x_{S}$ in $g_{1} (x)$ ein.
$y$	$=$	$- \frac{1}{2} \cdot (- 1) + 2$
$y$	$=$	$\frac{1}{2} + 2$
$y_{S}$	$=$	$2,5$

$\frac{2}{3} x + 2$	$=$	$\frac{1}{2} x + 3$	$- \frac{1}{2} x - 2$
$\frac{2}{3} x - \frac{1}{2} x$	$=$	$3 - 2$
	↓	Bringe die Brüche auf den kleinsten gemeinsamen Nenner.
$\frac{4}{6} x - \frac{3}{6} x$	$=$	$3 - 2$
$\frac{1}{6} x$	$=$	$1$	$: \frac{1}{6}$
$x$	$=$	$\frac{1}{\frac{1}{6}}$
	↓	Du dividierst durch einen Bruch $\to$ Multipliziere mit dem Kehrwert.
$x_{S}$	$=$	$6$

$\frac{3}{4} x + 1$	$=$	$\frac{1}{2} x + 2$	$- \frac{1}{2} x - 1$
$\frac{3}{4} x - \frac{1}{2} x$	$=$	$2 - 1$
	↓	Bringe die Brüche auf den kleinsten gemeinsamen Nenner .
$\frac{3}{4} x - \frac{2}{4} x$	$=$	$2 - 1$
$\frac{1}{4} x$	$=$	$1$	$: \frac{1}{4}$
$x$	$=$	$\frac{1}{\frac{1}{4}}$
	↓	Du dividierst durch einen Bruch $\to$ Multipliziere mit dem Kehrwert.
$x_{S}$	$=$	$4$

$y$	$=$	$3 x + 4$
$y$	$=$	$- 2 x + 14$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate des zu berechnen.
$3 x + 4$	$=$	$- 2 x + 14$	$+ 2 x; - 4$
$5 x$	$=$	$10$	$: 5$
$x$	$=$	$2$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate zu berechnen
$y$	$=$	$3 \cdot 2 + 4$
	↓	Punkt vor Strich beachten
$y$	$=$	$10$
	↓	$\Rightarrow$ Schnittpunkt: S(2\|10)

$y$	$=$	$6 x - 3$
$y$	$=$	$7 x - 11$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate zu berechnen.
$6 x - 3$	$=$	$7 x - 11$	$+ 3; - 7 x$
$- x$	$=$	$- 8$	$: (- 1)$
$x$	$=$	$8$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate zu berechnen.
$y$	$=$	$6 \cdot 8 - 3$
	↓	Punkt vor Strich beachten
$y$	$=$	$45$
	↓	$\Rightarrow$ Schnittpunkt: S(8\|45)

$y$	$=$	$8 x + 3$
$y$	$=$	$- 4 x + 6$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate des zu berechnen.
$8 x + 3$	$=$	$- 4 x + 6$	$- 3; + 4 x$
$12 x$	$=$	$3$	$: 12$
$x$	$=$	$\frac{3}{12} = \frac{1}{4}$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate des zu berechnen.
$y$	$=$	$8 \cdot \frac{1}{4} + 3$
	↓	Punkt vor Strich beachten
$y$	$=$	$5$
	↓	$\Rightarrow$ Schnittpunkt: S( $\frac{1}{4}$ \| $5$ )

$7 x - 14$	$=$	$7 x - 3$	$- 7 x$
$- 14$	$=$	$- 3$
	↓	falsche Aussage!

$y$	$=$	$\frac{1}{6} x - 4$
$y$	$=$	$\frac{1}{3} x - 10$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate zu berechnen
$\frac{1}{6} x - 4$	$=$	$\frac{1}{3} x - 10$	$- \frac{1}{3} x; + 4$
$- \frac{1}{6} x$	$=$	$- 6$	$: (- \frac{1}{6})$
$x$	$=$	$36$
	↓	Den x-Wert in eine der beiden Koordinaten einsetzen, um die y-Koordinate zu berechnen
$y$	$=$	$\frac{1}{3} \cdot 36 - 10$
	↓	Punkt vor Strich beachten
$y$	$=$	$2$
	↓	$\Rightarrow$ Schnittpunkt: S (36\|2)

$y$	$=$	$\frac{1}{2} x + \frac{3}{2}$
$y$	$=$	$\frac{1}{2}$
	↓	Die Geraden werden gleichgesetzt, um die x-Koordinate zu berechnen
$\frac{1}{2} x + \frac{3}{2}$	$=$	$\frac{1}{2}$	$- \frac{3}{2}$
$\frac{1}{2} x$	$=$	$- 1$	$\cdot 2$
$x$	$=$	$- 2$
	↓	Den x-Wert in eine der beiden Geraden einsetzen, um die y-Koordinate zu berechnen
$y$	$=$	$\frac{1}{2}$
	↓	$\Rightarrow$ Schnittpunkt: S(-2 \| 0,5)

Aufgaben zur Berechnung von Schnittpunkten von Geraden

Finde den Schnittpunkt

Lösung der Aufgabe

Hast du eine Frage oder Feedback?

Lösung der Aufgabe

Hast du eine Frage oder Feedback?

Zeichnung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimmung des Schnittpunkts

Zeichnung

Geradenschnittpunkte berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

Geradenschnittpunkt berechnen

Zeichnung

Hast du eine Frage oder Feedback?

f(x):y=mfx+bf

g(x):y=mgx+bg

h(x):y=mhx+bh

i(x):y=mix+bi

Hast du eine Frage oder Feedback?

Schnittpunkt P(xp|yp) von g und h

Hast du eine Frage oder Feedback?

Schnittpunkt T(xT|yT) von h und i

Schnittpunkt Q(xQ|yQ) von g und i

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimme den Schnittpunkt von g und h

Bestimme den Schnittpunkt von g und i

Hast du eine Frage oder Feedback?

Bestimme den Schnittpunkt von g und h

Bestimme den Schnittpunkt von g und i

Hast du eine Frage oder Feedback?

Bestimmung von Schnittpunkten

Hast du eine Frage oder Feedback?

Schnittpunkte ablesen

Hast du eine Frage oder Feedback?

Der Leuchtturm

Berechnung des Abstands an der Stelle x=0.

Hast du eine Frage oder Feedback?

Graphische Lösung

Modellieren der Lotgeraden

Hast du eine Frage oder Feedback?

Kürzester Abstand zwischen Schiff und Leuchtturm

Hast du eine Frage oder Feedback?

Schnittpunkte zweier Geraden berechnen

$f (x) : y = m_{f} x + b_{f}$

$g (x) : y = m_{g} x + b_{g}$

$h (x) : y = m_{h} x + b_{h}$

$i (x) : y = m_{i} x + b_{i}$

Schnittpunkt $P (x_{p} | y_{p})$ von g und h

Schnittpunkt $T (x_{T} | y_{T})$ von h und i

Schnittpunkt $Q (x_{Q} | y_{Q})$ von g und i

Berechnung des Abstands an der Stelle $x = 0$ .

$x - 1,5$	$=$	$- 2 x + 7,5$
	↓	Addiere zunächst 2x und anschließend 1,5.
$3 x$	$=$	$9$
	↓	Dividiere durch 3.
$x$	$=$	$3$

$x + 1$	$=$	$- \frac{1}{2} x - 2$	$+ \frac{1}{2} x - 1$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$x + \frac{1}{2} x$	$=$	$- 2 - 1$
	↓	Fasse zusammen.
$\frac{3}{2} x$	$=$	$- 3$	$: \frac{3}{2}$
$x$	$=$	$- 2$

$x + 1$	$=$	$\frac{5}{3} x + \frac{7}{3}$	$- \frac{5}{3} x - 1$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$x - \frac{5}{3} x$	$=$	$\frac{7}{3} - 1$
	↓	Fasse zusammen.
$- \frac{2}{3} x$	$=$	$\frac{4}{3}$	$: (- \frac{2}{3})$
$x$	$=$	$- 2$

$\frac{1}{6} x + \frac{3}{2}$	$=$	$- \frac{2}{3} x + 2$	$+ \frac{2}{3} x - \frac{3}{2}$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$\frac{1}{6} x + \frac{2}{3} x$	$=$	$2 - \frac{3}{2}$
	↓	Fasse zusammen.
$\frac{5}{6} x$	$=$	$\frac{1}{2}$	$: \frac{5}{6}$
$x$	$=$	$\frac{3}{5}$

$\frac{1}{6} x + \frac{3}{2}$	$=$	$2 x - 3$	$- 2 x - \frac{3}{2}$
	↓	Sortiere nach $x$ -Termen und Zahlen.
$\frac{1}{6} x - 2 x$	$=$	$- 3 - \frac{3}{2}$
	↓	Fasse zusammen.
$- \frac{11}{6} x$	$=$	$- \frac{9}{2}$	$: (- \frac{11}{6})$
$x$	$=$	$\frac{9}{2} \cdot \frac{6}{11} = \frac{27}{11}$

$y_{L o t}$	$=$	$- 2 x + b$
	↓	Einsetzen von $L (4 \| 8)$
$8$	$=$	$- 2 \cdot 4 + b$
$8$	$=$	$- 8 + b$	$+ 8$
$16$	$=$	$b$

$y$	$=$	$y_{L o t}$
$0,5 x + 1$	$=$	$- 2 x + 16$	$- 16$
$0,5 x - 15$	$=$	$- 2 x$	$- 0,5 x$
$- 15$	$=$	$- 2,5 x$	$\cdot (- 1)$
$15$	$=$	$2,5 x$	$: 2,5$
$6$	$=$	$x$