Aufgaben zu Kreisen und Kreisteilen
Hier findest du Aufgaben zu Kreisen und Kreisteilen. Vertiefe dein Wissen, damit alles rund läuft!
- 1
Wähle die richtige Antwort aus.
Wie berechnet man den Flächeninhalt von einem Kreis mit Radius ?
Welche Formel stimmt? (Mit ist der Flächeninhalt vom Kreis gemeint.)
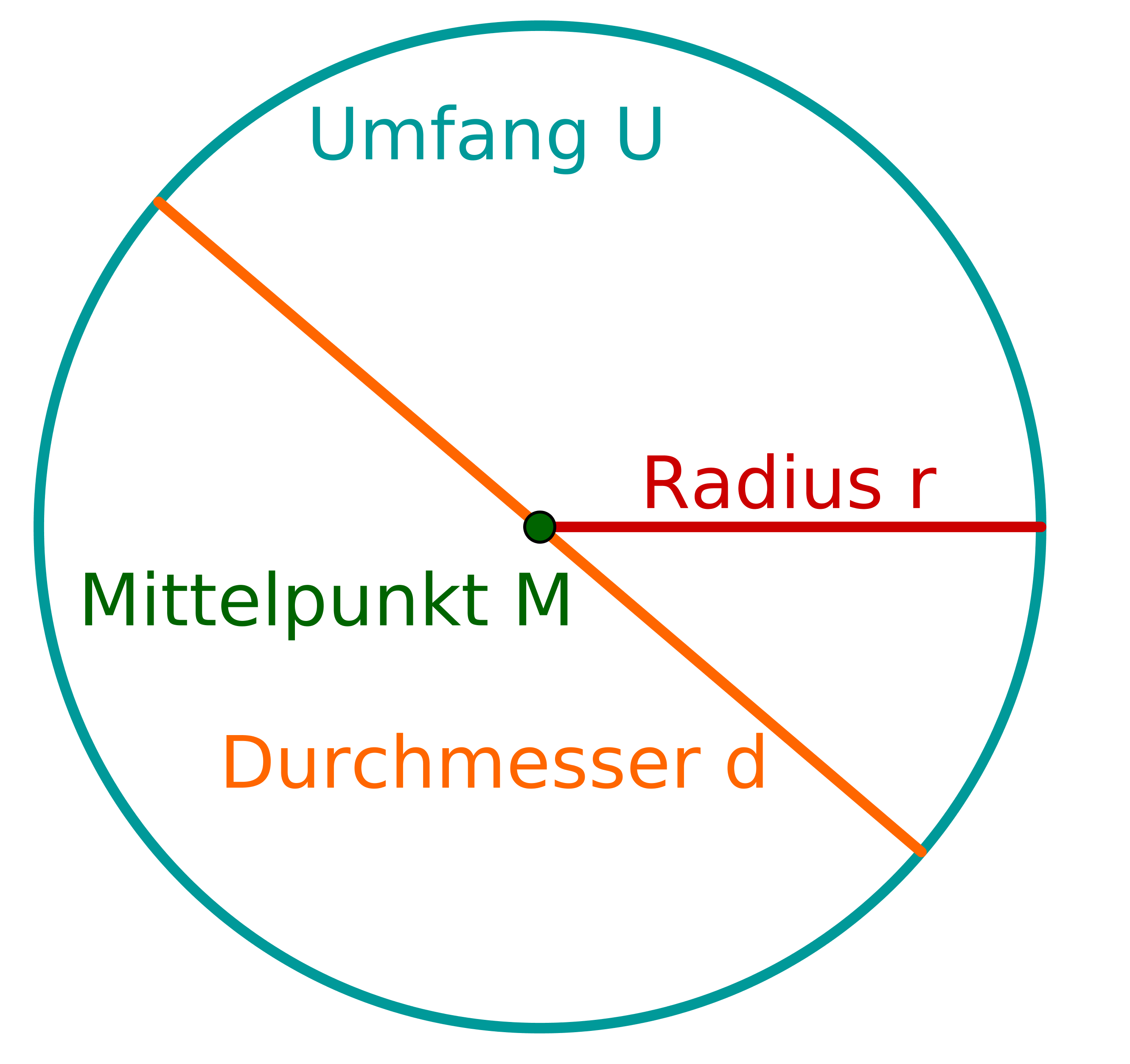
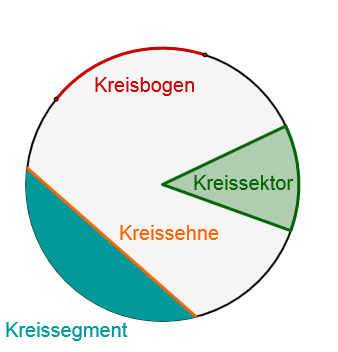
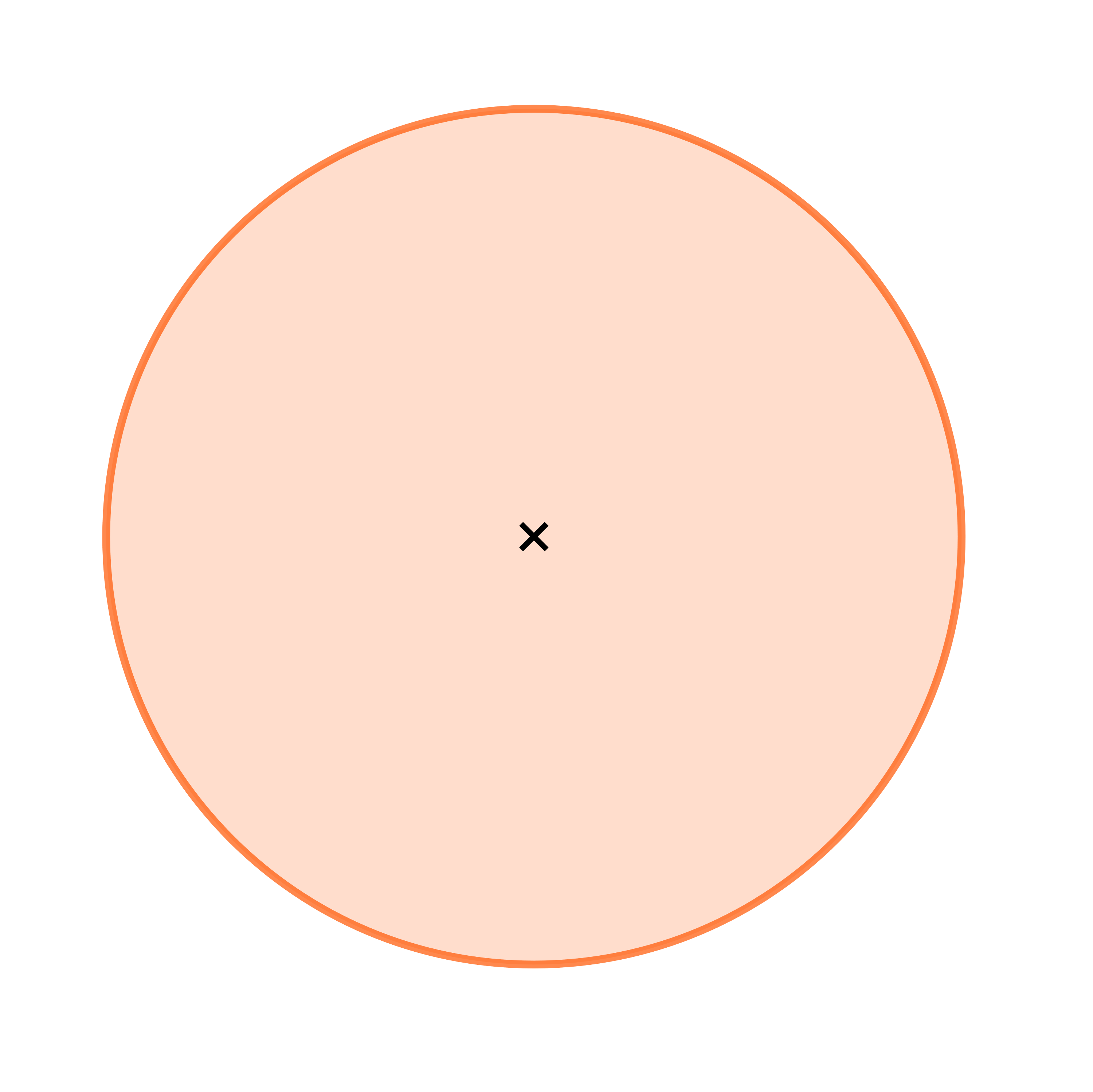
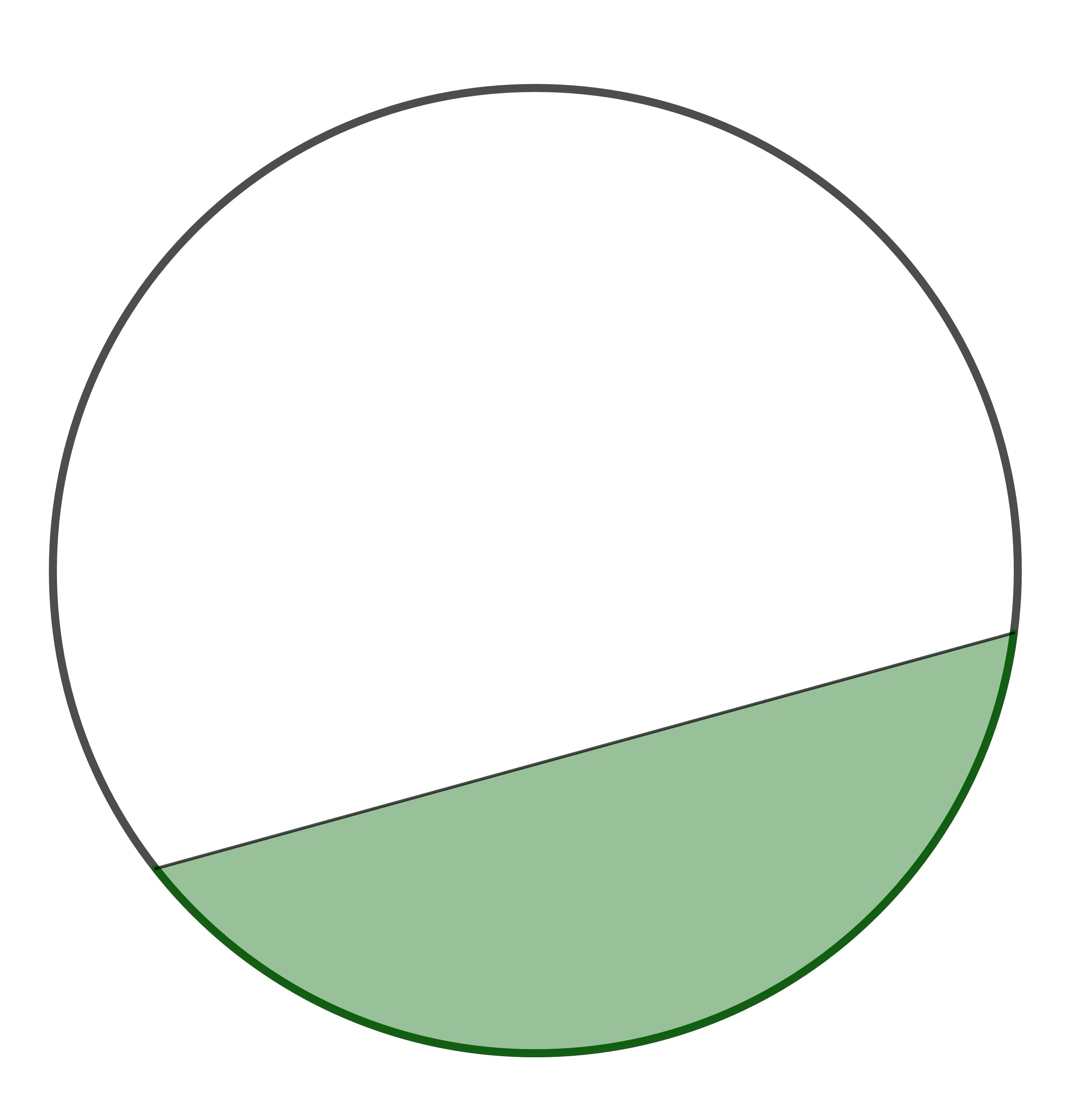
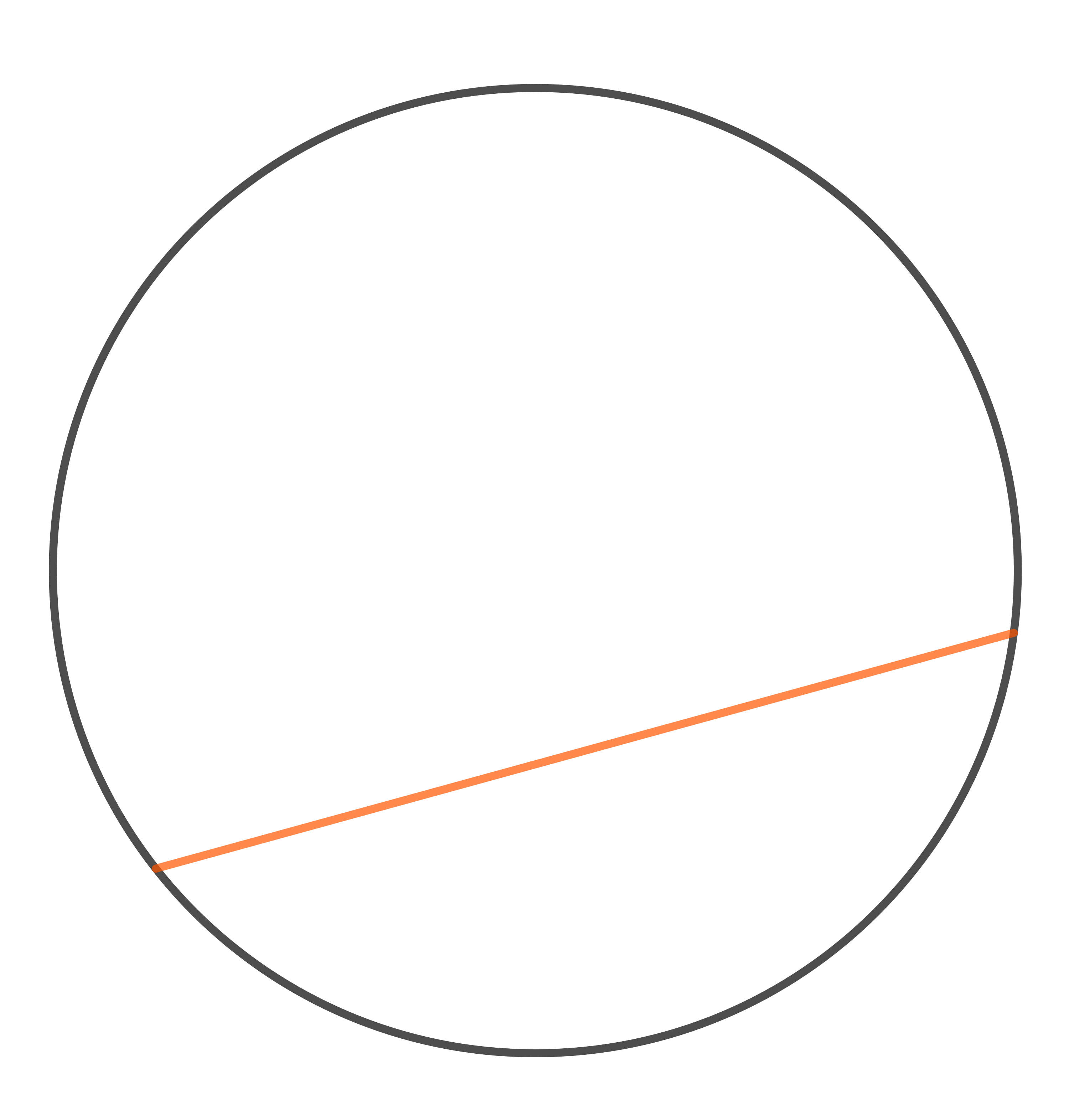
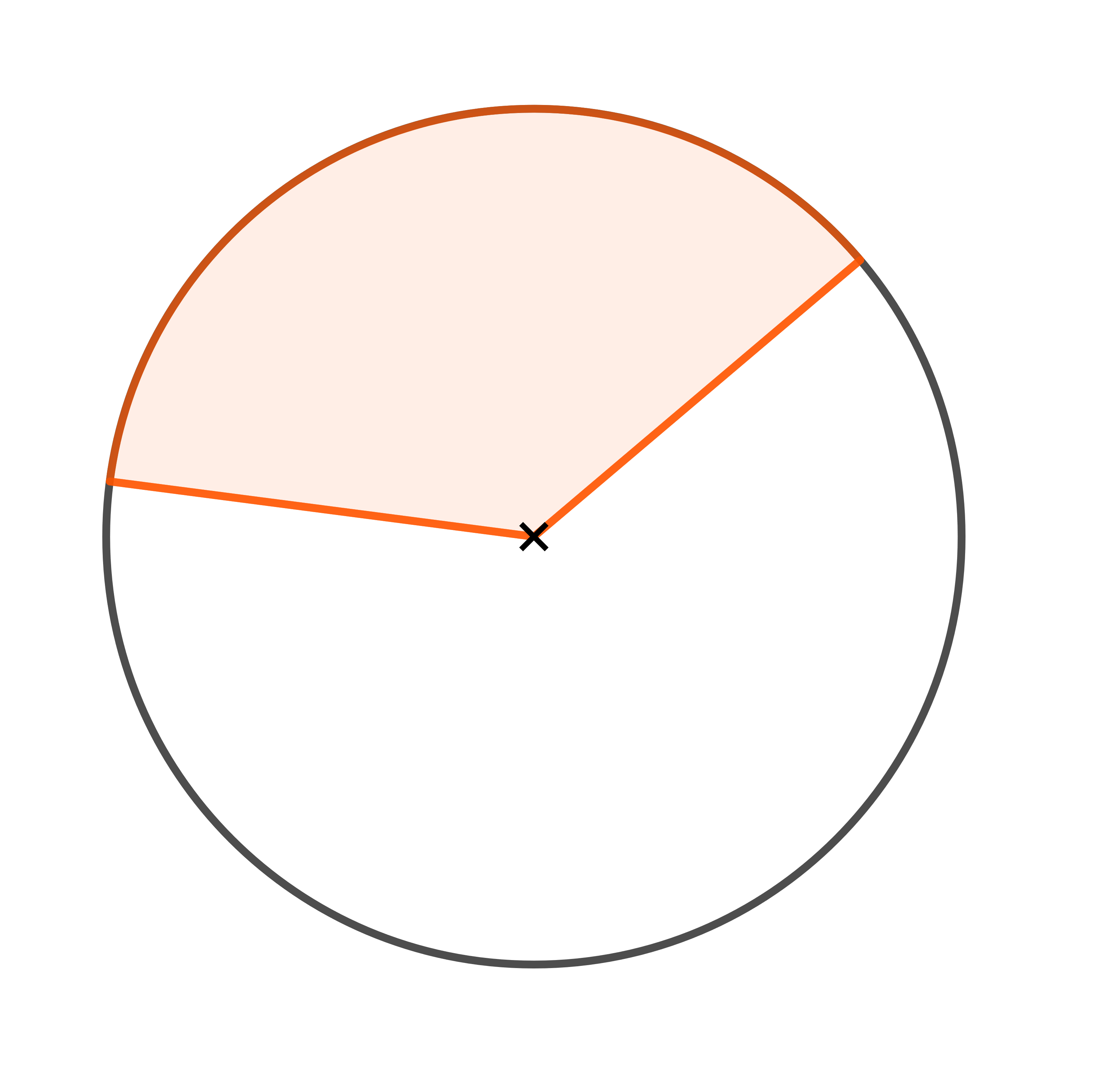
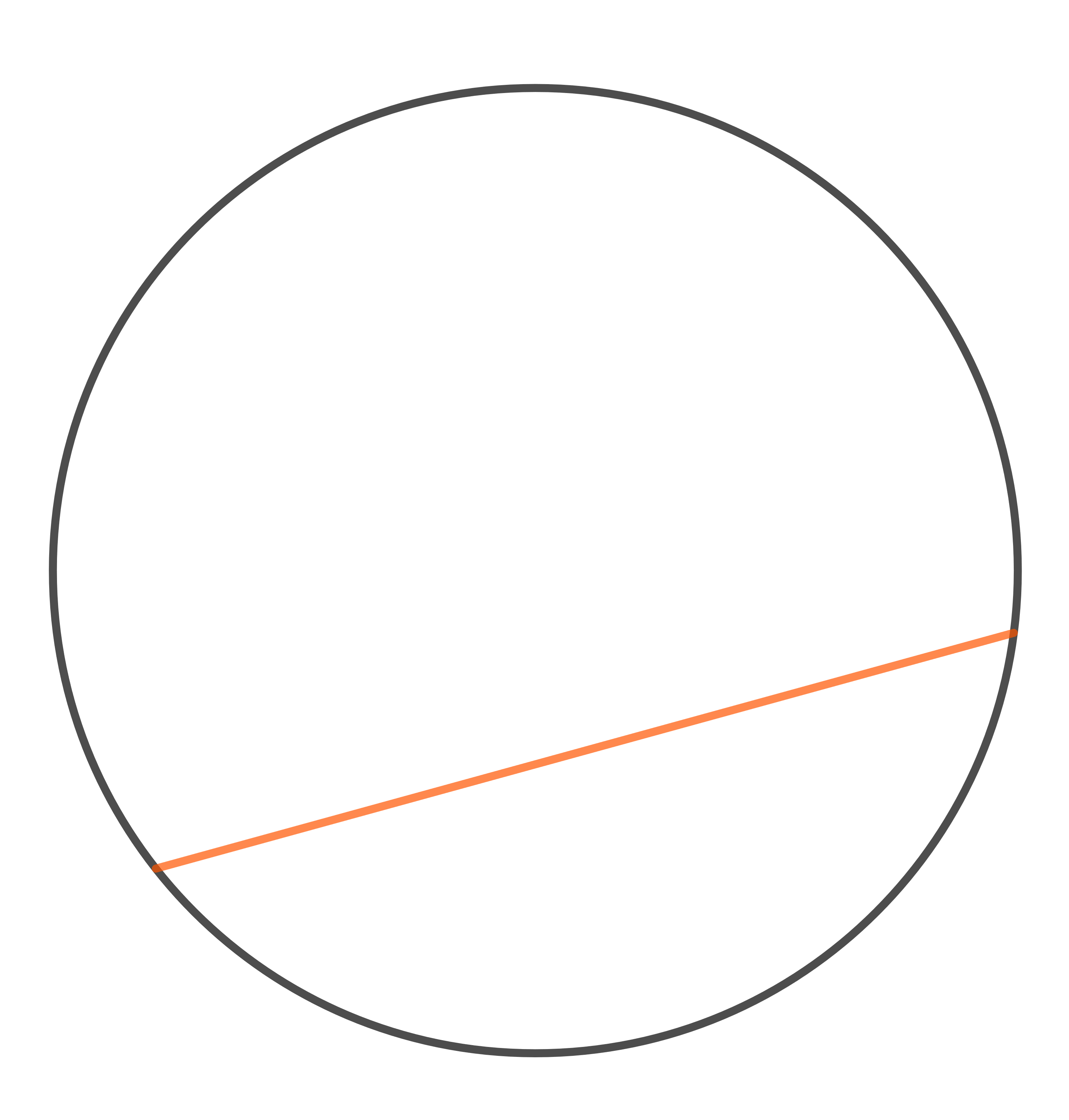
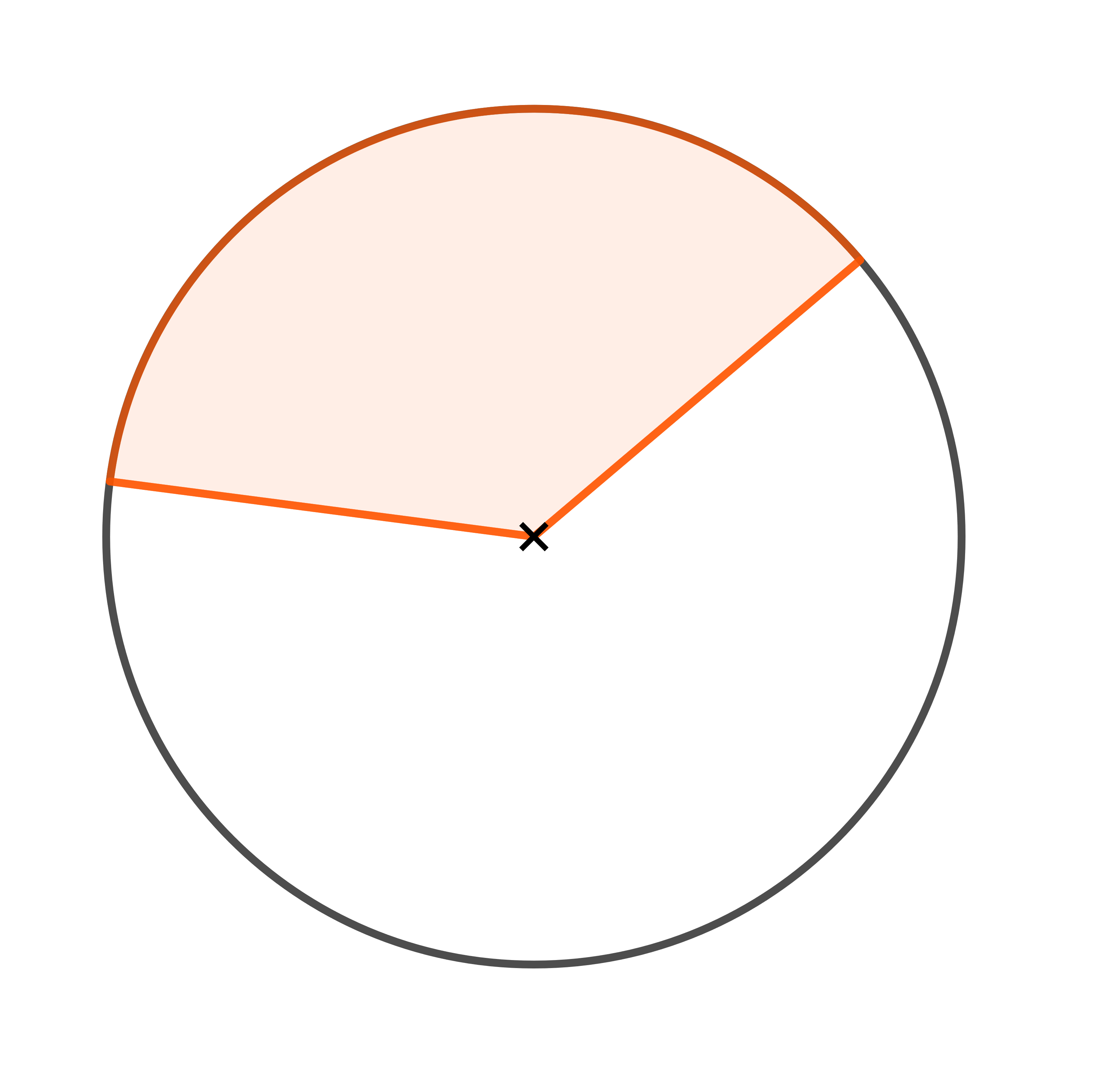
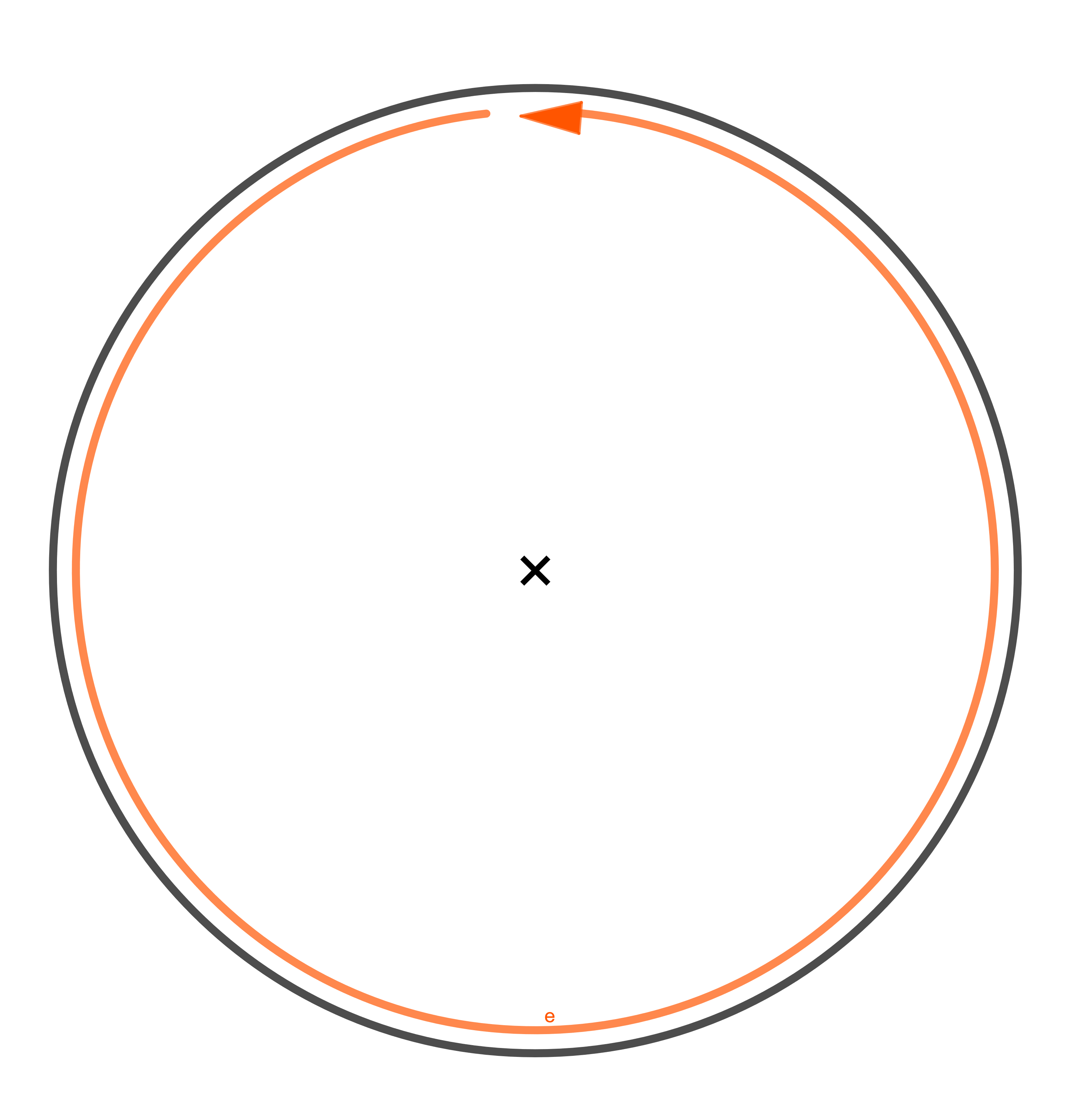
Auf welchem Bild ist ein Kreissegment dargestellt?
- 2
Berechne von den folgenden geometrischen Körpern/Figuren den Radius .
Ein Kreis hat den Umfang . Berechne den Radius . Runde das Ergebnis auf drei Dezimalstellen genau.
Ein Kreis hat die Fläche . Berechne den Radius in , runde dabei auf ganze !
- 3
Zeichne dieses Mandala mit dem Zirkel.
- 4
Zeichne die folgende Figur mit dem Zirkel nach. Du kannst die Zeichnung selbstverständlich in den Grautönen deines Zirkels belassen. Tipp: der Radius der orangen Halbkreise beträgt 1cm.
- 5
Zeichne folgende Figuren auf ein kariertes Blatt Papier. Nutze Zirkel und Lineal.
- 6
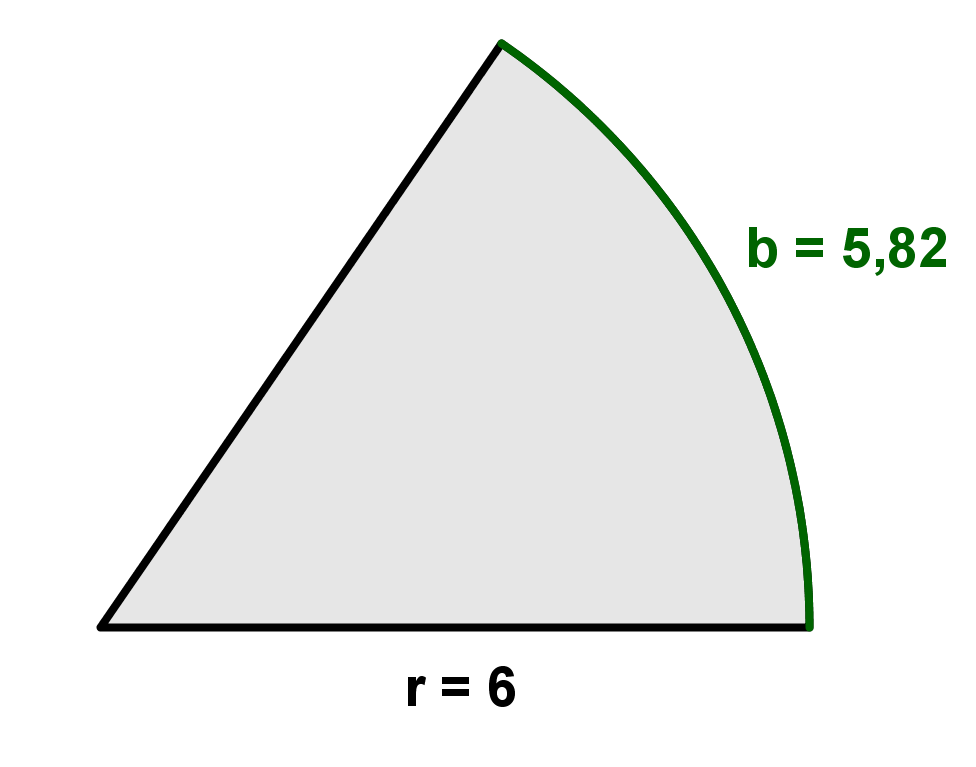
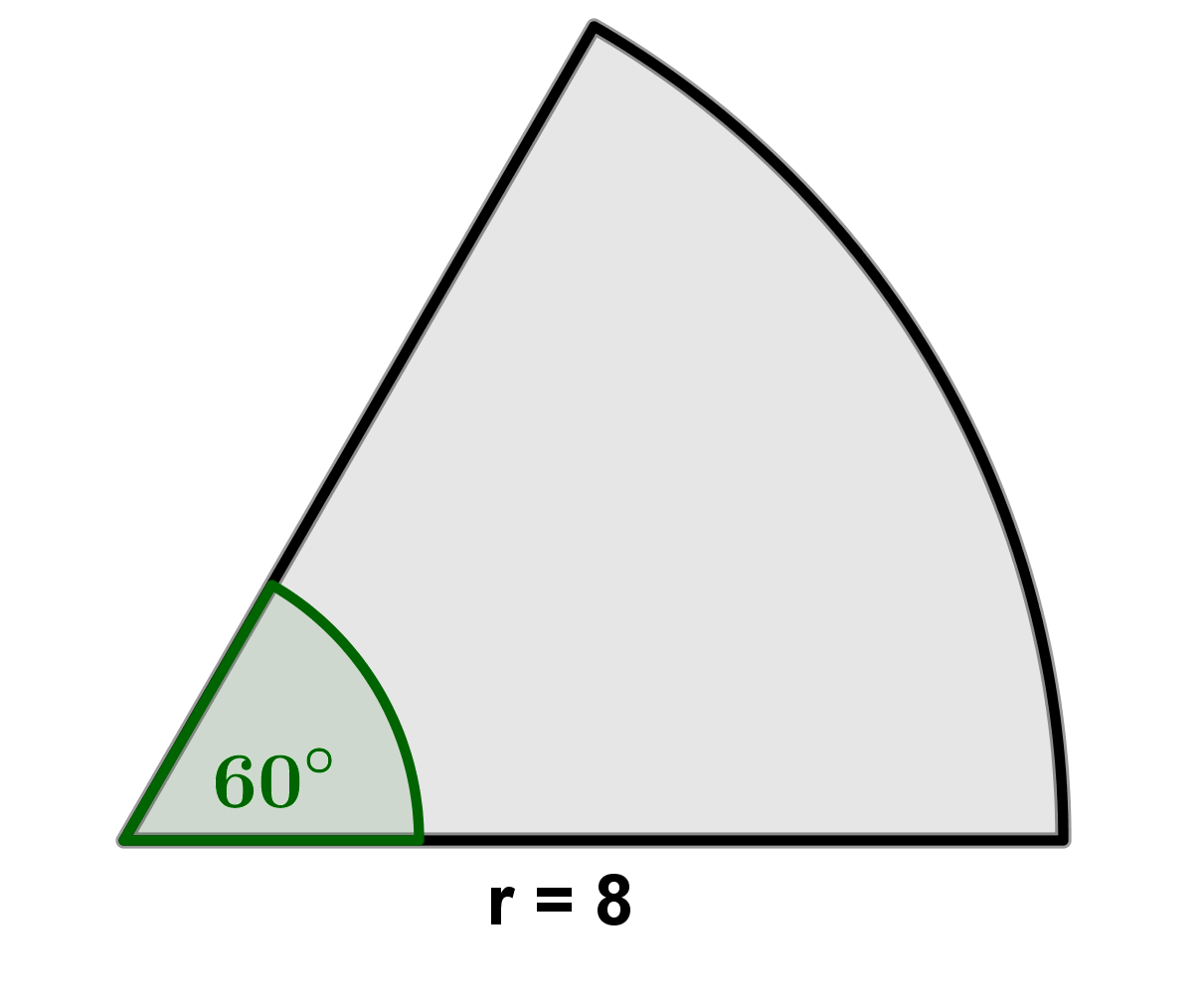
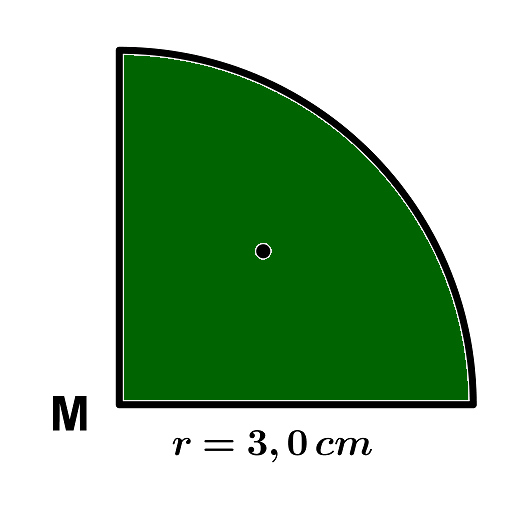
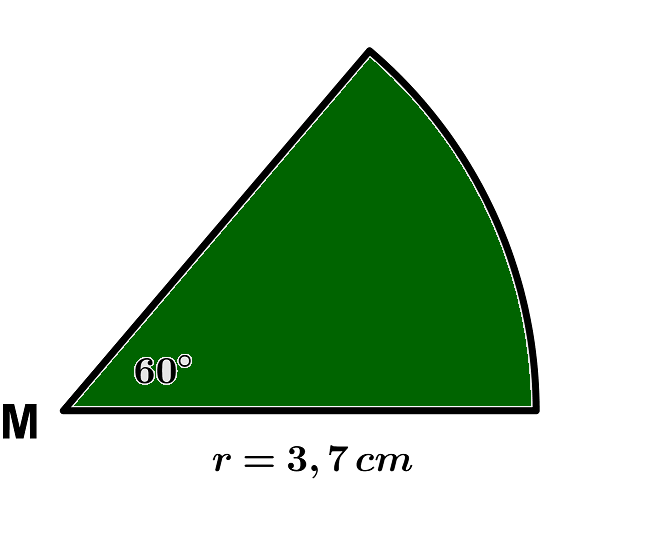
Bestimme den Flächeninhalt der folgenden Kreissektoren. Gib deine Lösungen auf zwei Stellen nach dem Komma gerundet ein.
- 7
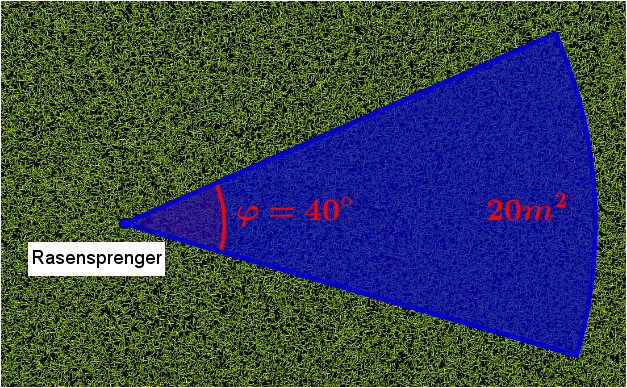
Der abgebildete Rasensprenger schwenkt um 40° und besprüht so eine Rasenfläche von .
Wie groß ist seine Reichweite?
Gib das Ergebnis auf zwei Stellen nach dem Komma gerundet ein.

Quelle: Sebastian & Kari, CC BY-SA 2.0, Wikimedia Commons
m - 8
- 9
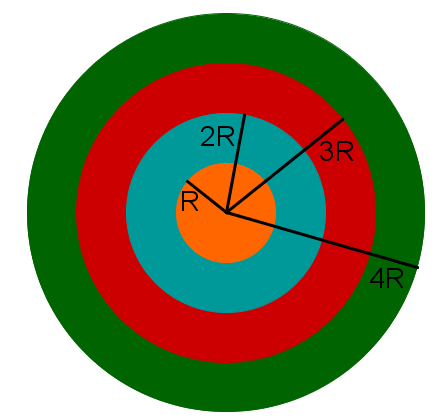
Begründe, wie sich jeweils Umfang und Flächeninhalt eines Kreises ändern, wenn man seinen Radius verdoppelt, verdreifacht bzw. vervierfacht.
- 10
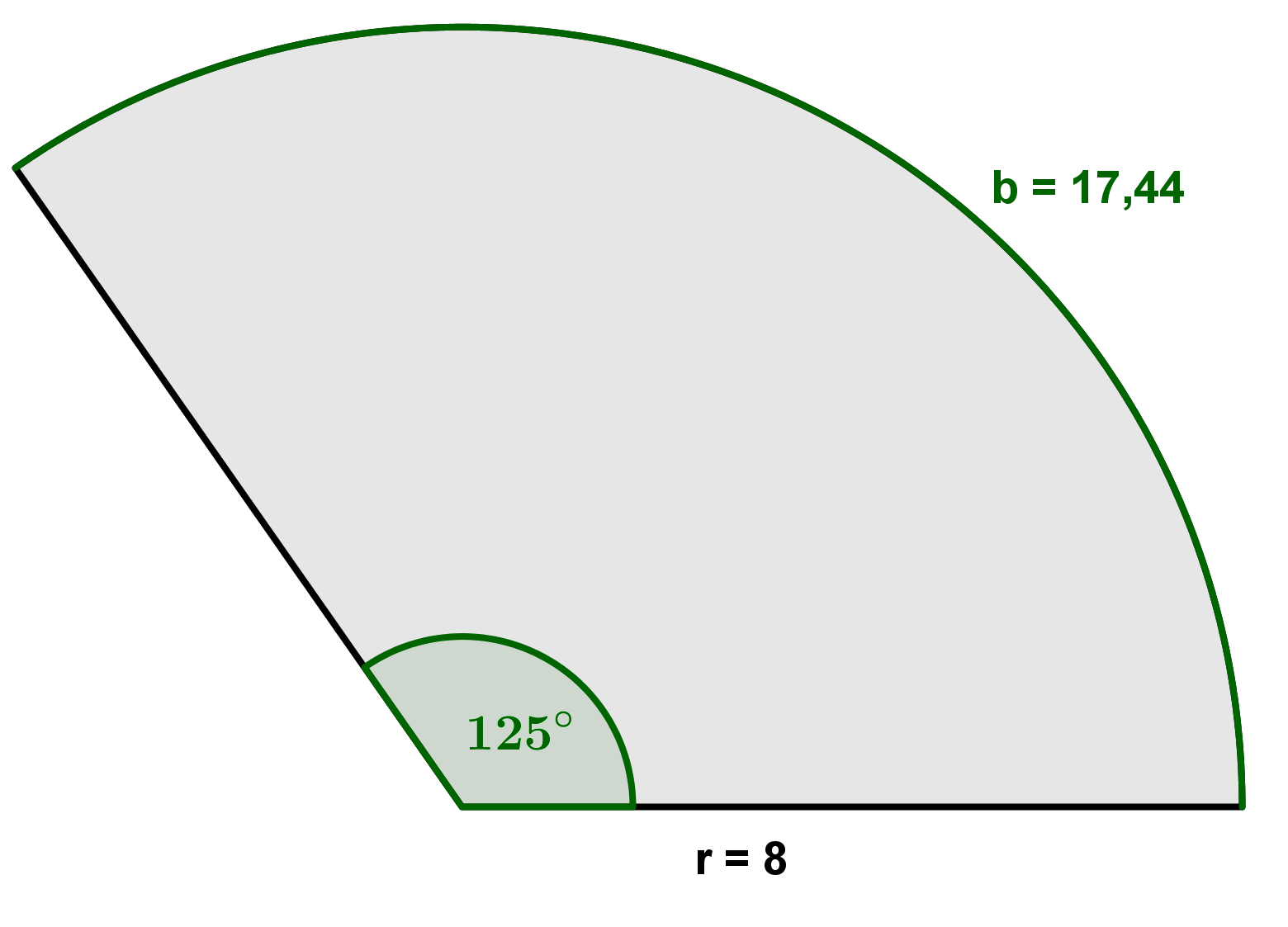
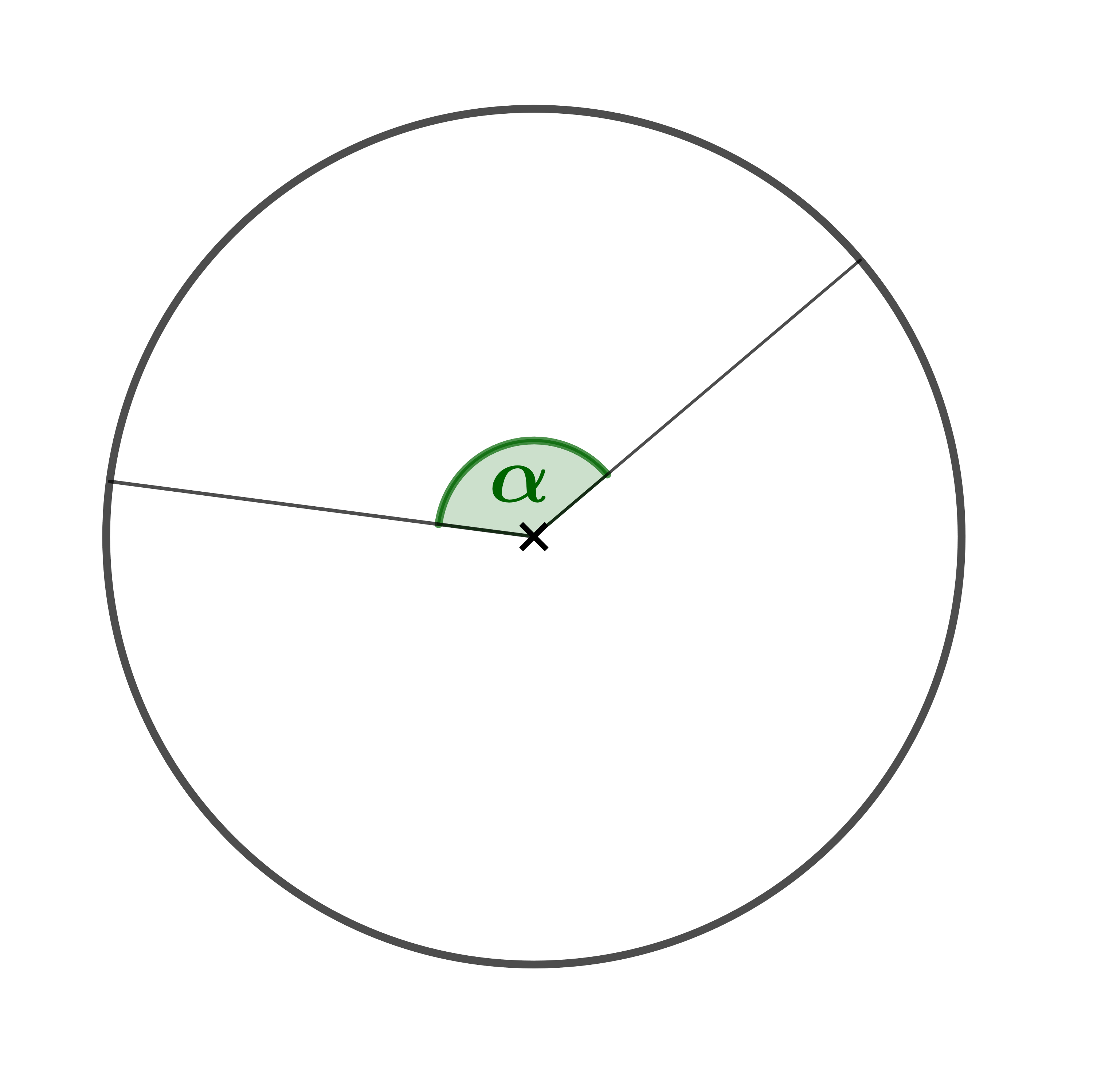
In einem Kreis mit Radius ist ein Sektor mit Mittelpunktswinkel eingezeichnet.
Gib die Fläche des Sektors und die Länge des zugehörigen Bogens an.
- 11
Stelle jeweils einen Funktionsterm auf, der den Flächeninhalt A und den Umfang U eines Viertelkreises in Abhängigkeit vom Radius r beschreibt.
- 12
Berechne die Fläche des markierten Kreissegments. Dabei ist der Radius und . Runde deine Lösung auf ganze .
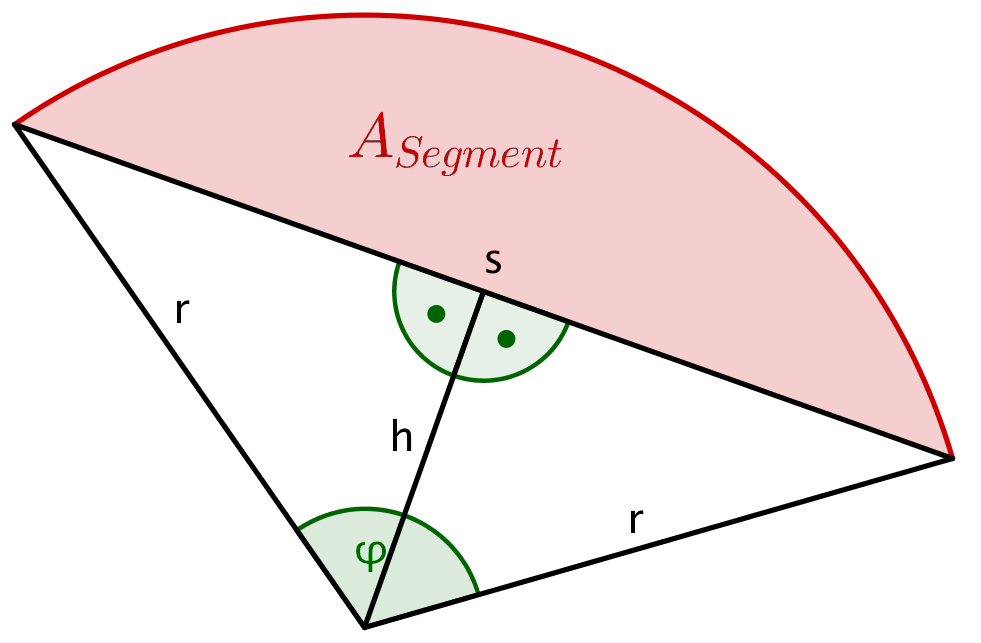
- 13
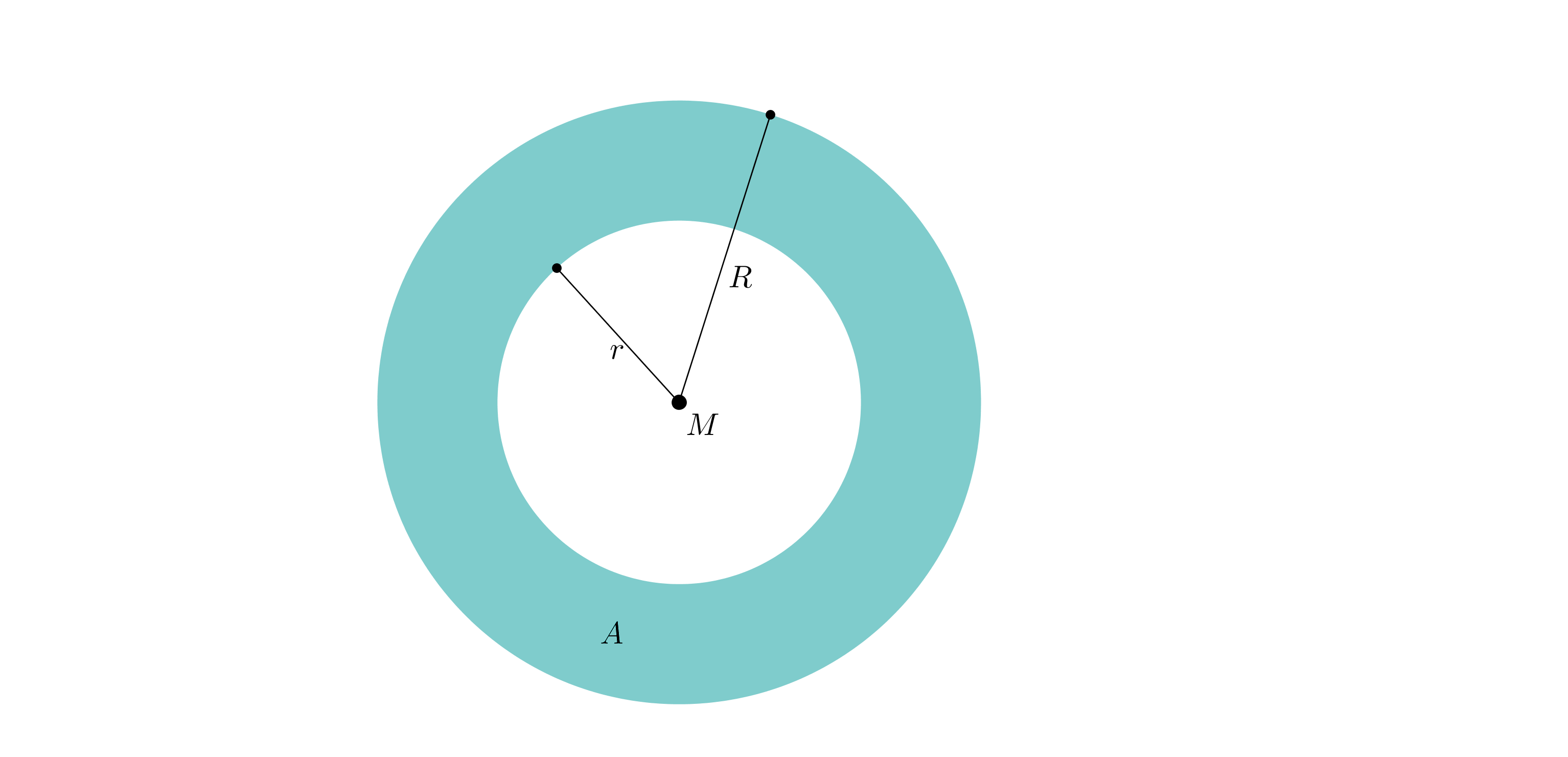
Bei einem Kreisring beträgt der Außenradius 10 cm. Stelle einen Funktionsterm auf, der den Flächeninhalt A des Kreisrings in Abhängigkeit vom Innenradius r beschreibt. Welche Werte für r ergeben eine sinnvolle Einsetzung?
- 14
Ein runder Tisch zum Ausziehen hat einen Durchmesser von . Er kann durch rechteckige Einlegeplatten, die jeweils breit sind, vergrößert werden (siehe Skizze).
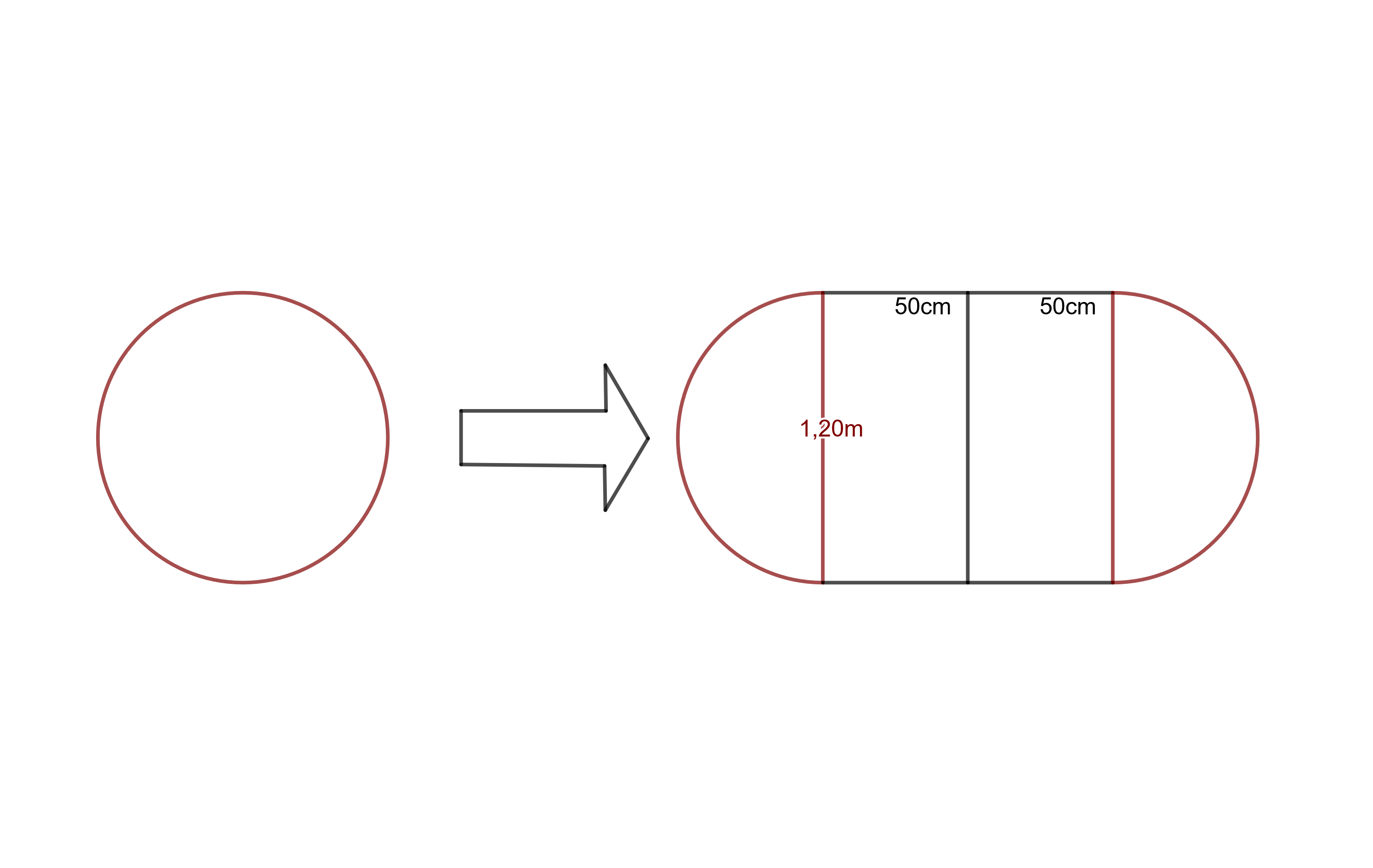
Berechne den Flächeninhalt und den Umfang der vergrößerten Tischplatte.
Für den ausgezogenen Tisch soll eine Tischdecke gekauft werden, die überall mindestens überhängt. Welche der angebotenen Tischdecken eignet sich?
140 cm
260 cm
150 cm
250 cm
160 cm
240 cm
- 15
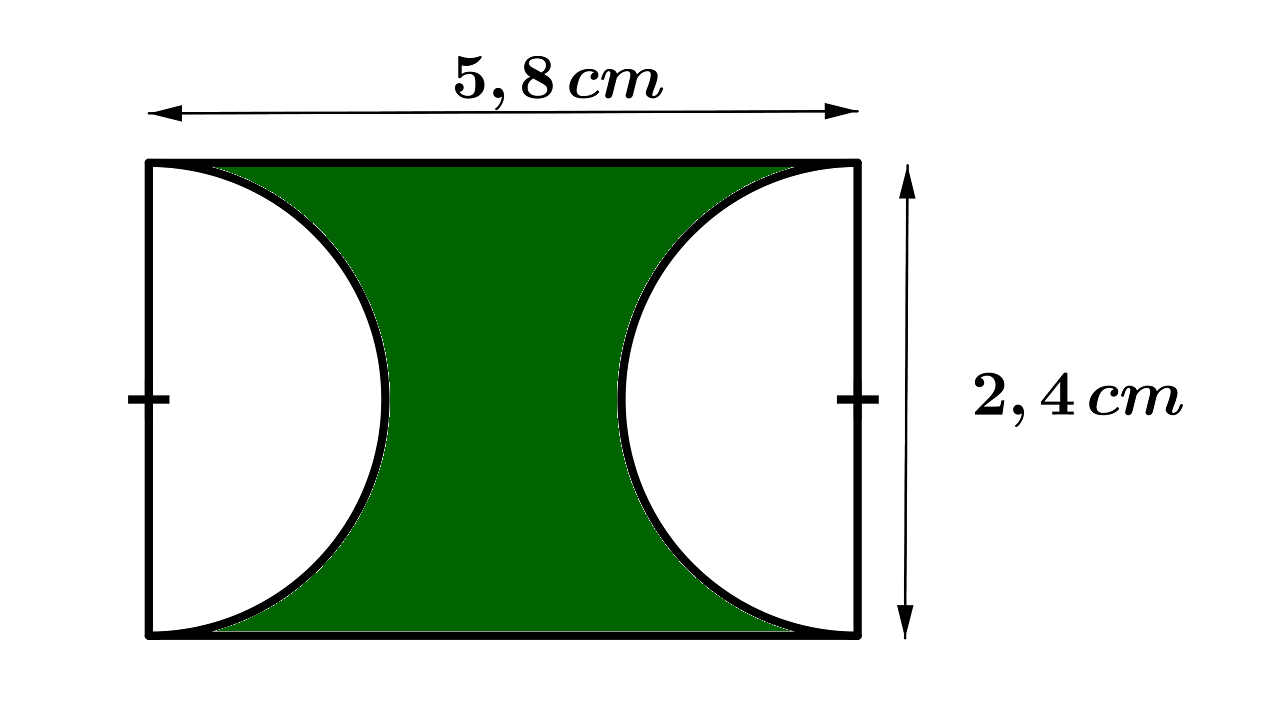
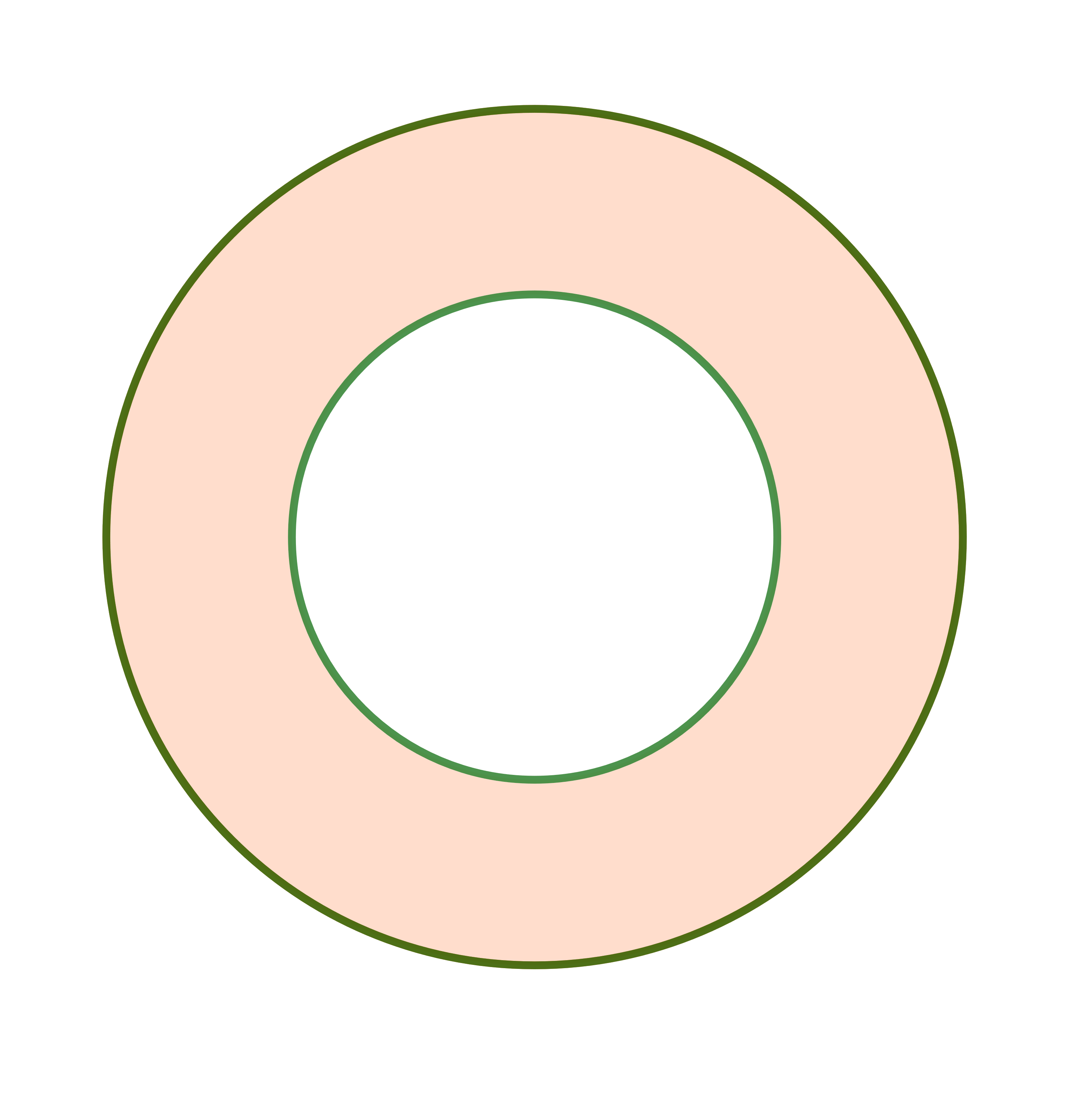
Berechne die Fläche des (grünen) Kreisrings. Die eingezeichnete Sehne hat eine Länge von .
- 16
Wie viele Kreise kannst du zählen?
- 17
Bauer Heinrich hat zwei Schafe Berta und Paula.
Für jedes Schaf hat er auf einer Wiese einen Pflock, an den er das Schaf an diesem Morgen mit einem Strick anbindet.
Der erste Pflock befindet sich im Punkt . Daran bindet der Bauer das Schaf Berta mit einem langen Strick an. Welcher Bereich kann von Berta abgefressen werden?
Zeichne diesen Bereich in ein Koordinatensystem ein. Färbe den Bereich grün.
Der zweite Pflock befindet sich im Punkt . Hier befestigt der Bauer das Schaf Paula mit einem langen Strick. Welcher Bereich kann von Paula abgefressen werden? Zeichne diesen Bereich ebenfalls in das Koordinatensystem ein und färbe ihn grün.
Kommen sich die zwei Schafe in die Quere ?
- 18
Quiz zu Kreisteilen
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?