Aufgaben zu quadratischen Gleichungen mit Parametern
Hier findest du gemischte Übungsaufgaben zu quadratischen Gleichungen mit Parametern. Lerne, Gleichungen mit Parametern zu lösen!
- 1
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel mit Parametern
Forme die quadratische Gleichung so um, dass auf einer Seite die Null steht, und fasse so weit wie möglich zusammen.
Lies die Werte der Koeffizienten , und ab. Beachte, dass das auf der linken Seite dem aus der allgemeinen Form entspricht.
Im Sonderfall fällt der Term mit weg und es ergibt sich eine lineare Gleichung. Diesen Fall betrachtest du unten gesondert.
Sei nun :
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen, indem du sie gleich Null setzt.
Du kannst als eine Gerade mit negativer Steigung betrachten und so das Vorzeichenverhalten der Diskriminante bestimmen. Dadurch erhältst du eine Aussage über die Anzahl der Lösungen.
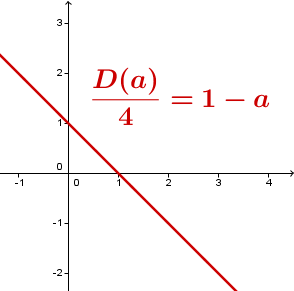
Dabei ist ein Spezielfall, den du getrennt betrachten musst.
zwei Lösungen
eine Lösungen
keine Lösung
Spezialfall
Wende die nun Mitternachtsformel an.
Sei nun :
In diesem Fall fällt der Term mit weg und es ergibt sich eine lineare Gleichung.
Diese kannst du durch Äquivalenzumformung lösen.
Ergebnis:
- 2
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel mit Parametern
Forme die quadratische Gleichung so um, dass auf einer Seite die Null steht.
Fasse die Summanden mit zusammen indem du ausklammerst.
Lies , und ab.
Berechne die Diskriminante der Gleichung. Dabei hilft dir die zweite binomische Formel .
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen, indem du quadratisch ergänzt .
Du erkennst, dass als Quadrat immer größer oder gleich Null ist und somit die Diskriminante insgesamt immer größer als Null ist, so dass für alle zwei Lösungen existieren.
zwei Lösungen für alle
Wende nun die Mitternachtsformel an.
- 3
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel
Forme die quadratische Gleichung
so um, dass auf einer Seite die Null steht, und fasse so weit wie möglich zusammen.
Lese , und ab.
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen, indem du sie gleich Null setzt.
Da eine Gerade mit positiver Steigung ist, kannst du das Vorzeichenverhalten der Diskriminante bestimmen und erhältst somit eine Aussage über die Anzahl der Lösungen.
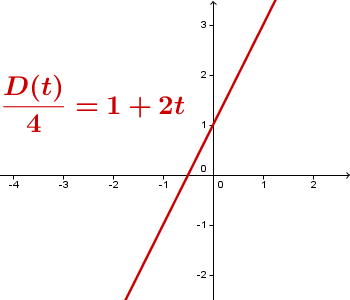
zwei Lösungen
eine Lösung
keine Lösung
Wende nun die Mitternachtsformel an, aber beachte dabei die verschiedenen Fälle für die Werte von .
keine Lösung
- 4
Löse die quadratische Gleichung in Abhängigkeit von den Parametern und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: die Mitternachtsformel
Forme die quadratische Gleichung so um, dass auf einer Seite die Null steht.
Lese die Koeffizienten , und der allgemeinen Form ab.
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von und auf ihr Vorzeichen, indem du sie gleich Null setzt.
oder
Da die Diskriminante eine nach oben geöffnete Parabel darstellt, kannst du daran das Vorzeichenverhalten ablesen.
Ist oder , dann ist und es gibt zwei Lösungen. Ist oder , so ist und es gibt genau eine Lösung. Für ist , also gibt es keine Lösung.
Wende nun die Mitternachtsformel an, um die Lösungen zu bestimmen. Beachte dabei aber die verschiedenen Fälle von oben
Für oder ist:
Für oder ist:
Ist stattdessen , dann gibt es keine Lösung.
- 5
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: quadratische Gleichungen
Da auf einer Seite der Gleichung
bereits Null steht, kannst du sofort die Parameter , und der allgemeinen Form ablesen. Und zwar gilt:
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen:
Da gilt, ist und ebenso das Quadrat größer als . Somit ist der Term größer als . Folglich ist die Diskriminante für jeden Wert von kleiner als Null. Daran kannst du also erkennen, dass es keine Lösungen gibt.
- 6
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parameter in quadratischen Gleichungen
In der Gleichung steht bereits auf einer Seite die Null. Hier kannst du nichts mehr zusammenfassen. Jetzt kannst du a,b und c ablesen.
Berechne die Diskriminante der Gleichung.
Betrachte das Vorzeichen der Diskriminante in Abhängigkeit vom Parameter und leite daraus die Anzahl der Lösungen her. Beachte dabei, dass im Fall die allgemeingültige Gleichung entsteht und du somit jedes einsetzen kannst.
- 7
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel mit Parametern
Bei dieser Gleichung steht auf einer Seite bereits die Null. Hier kannst du nichts mehr ausklammern. Jetzt kannst du a,b und c ablesen.
Der Fall ist laut Aufgabenstellung ausgeschlossen. Er muss also nicht explizit untersucht werden.
Berechne die Diskriminante der Gleichung.
Untersuche das Vorzeichenverhalten von und leite daraus die Anzahl der Lösungen her.
Setze in die Mitternachtsformel ein.
- 8
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: die Mitternachtsformel
Auf der einen Seite der Gleichung steht bereits eine Null. Lies also die Parameter und aus der allgemeinen Form von quadratischen Gleichungen ab.
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen, indem du sie gleich Null setzt. Dabei ist die dritte binomische Formel hilfreich.
oder
Da die Diskriminante in Abhängigkeit von eine nach oben geöffnete Parabel darstellt, bestimmst du das Vorzeichenverhalten der Diskriminante anhand ihrer Nullstellen und leitest darüber die Anzahl der Lösungen in Abhängigkeit vom Parameter her.
Ist oder , dann ist größer also und es gibt zwei Lösungen. Ist oder , dann ist die Diskriminante gleich , sodass genau eine Lösung existiert. Ist stattdessen , so gibt es keine Lösung.
Wende nun die Mitternachtsformel auf die verschiedenen Fälle an, um die Lösungen jeweils zu bestimmen.
Für oder ist
Für oder
Für existieren keine Lösungen.
- 9
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformel mit Parametern
Erkenne, dass auf einer Seite die Null steht und du nichts mehr ausklammern kannst.
Lies , und ab. Beachte, dass auch als Parameter in der allgemeinen Form der quadratischen Gleichungen vorkommt.
Im Sonderfall fällt der Term mit weg und es ergibt sich eine lineare Gleichung. Diesen Fall betrachtest du unten gesondert.
Sei nun :
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen, indem du sie gleich Null setzt.
Da eine Gerade mit negativer Steigung in ist, kannst du das Vorzeichenverhalten der Diskriminante bestimmen und erhältst somit eine Aussage über die Anzahl der Lösungen.
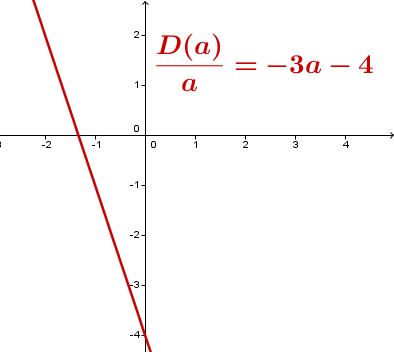
zwei Lösungen
eine Lösung
keine Lösung
Wende nun die Mitternachtsformel an.
für
für
für
Sei nun .
In diesem Fall erhältst du eine lineare Gleichung. Setze dazu in die Gleichung ein und löse sie auf.
Ergebnis:
für
für
für
für
- 10
Löse die quadratische Gleichung in Abhängigkeit vom Parameter .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mitternachtsformeln mit Parametern
Forme die quadratische Gleichung so um, dass auf einer Seite die Null steht, und fasse zusammen.
Fasse die Terme mit zusammen indem du den Faktor x ausklammerst.
Lies , und ab.
Berechne die Diskriminante der Gleichung.
Überprüfe die Diskriminante in Abhängigkeit von auf ihr Vorzeichen, indem du beachtest, dass ein Quadrat immer größer oder gleich als Null ist, und leite daraus die Anzahl der Lösungen her.
zwei Lösungen für alle m
Wende nun die Mitternachtsformel an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


