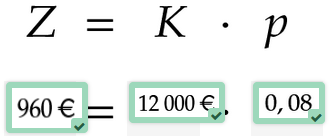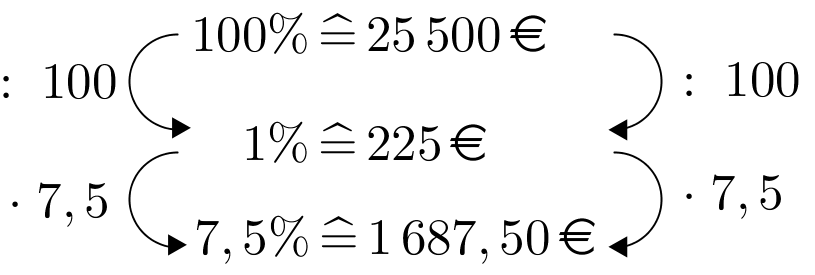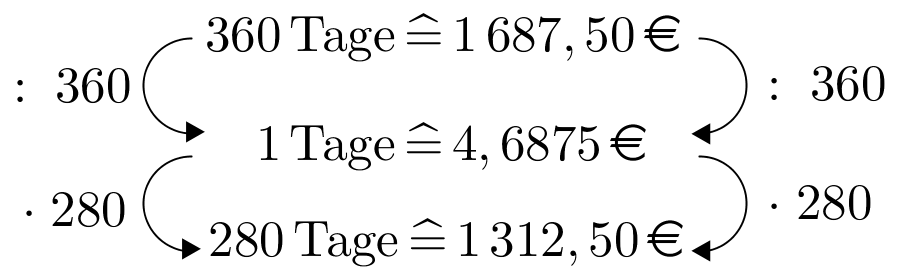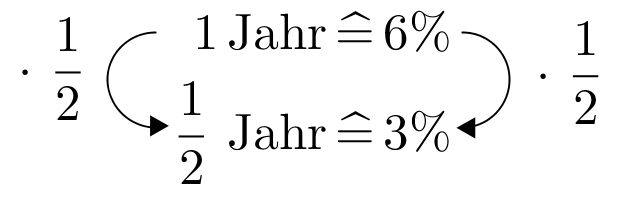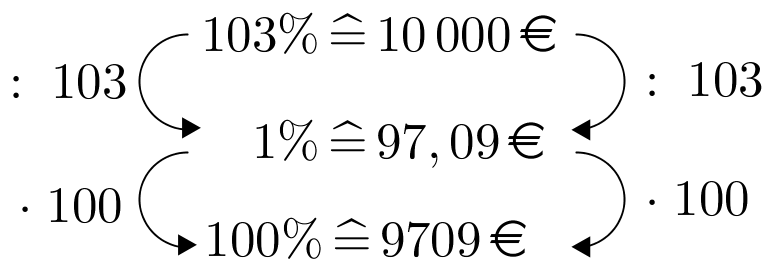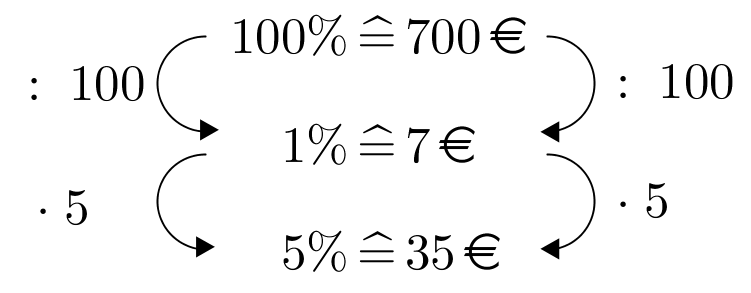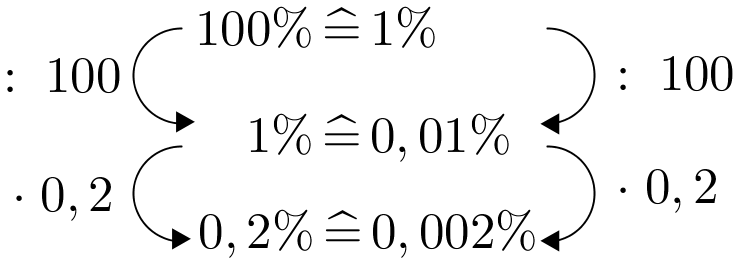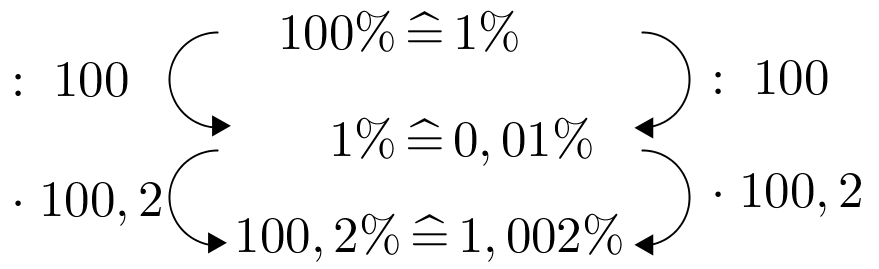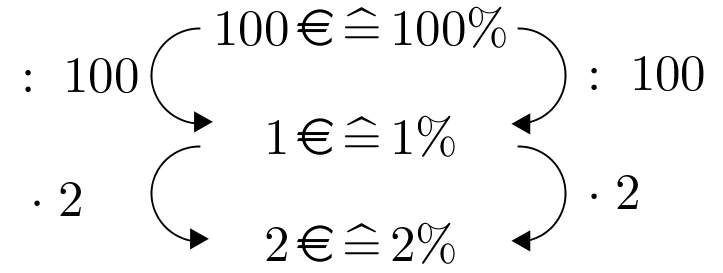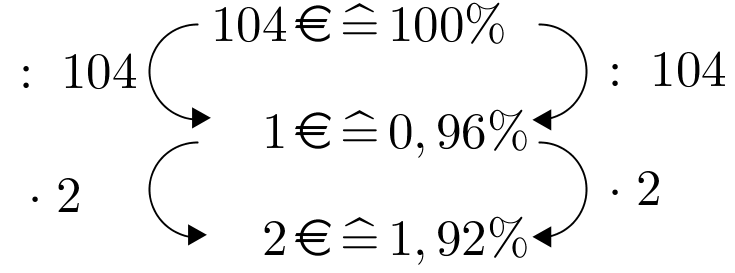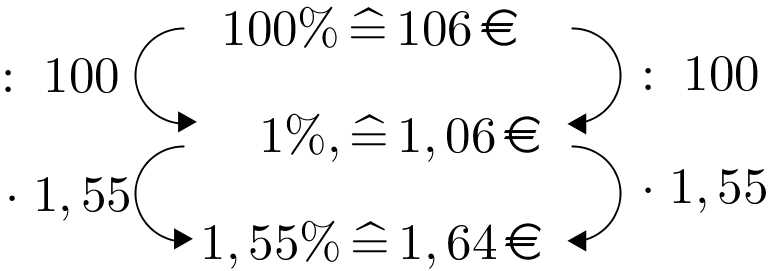Aufgaben zur Zinsrechnung
Wiederhole wichtige Grundlagen und übe mit diesen gemischten Aufgaben zum Thema Zinsrechnung!
- 1
Hohe Zinsen!
Peter legt bei einer Bank an und bekommt Zinsen.
Bestimme aus der Aufgabenstellung den Zins , das Kapital und den Zinssatz
Setze die Beträge richtig ein.
Peter hat den Überblick über sein Kapital verloren. In einem Jahr erhält er für Zinsen
Berechne das Kapital, nachdem er Zinsen bekommen hat.
€
- 2
Ein Drittel eines Kapitals wird zu 5% angelegt. Ein weiteres Neuntel zu 4% und der Rest zu 4.5%. Der gesamte Zinsertrag beläuft sich auf 2282,50 Euro. Wie groß ist das Anfangskapital?
€ - 3
Zum Bau eines Einfamilienhauses benötigt Familie Koch eine Hypothek von 150000 €. Die Zinsen für die ersten 5 Jahre sind auf 6% pro Jahr festgelegt. Außerdem muss Familie Koch 1% Tilgung pro Jahr zahlen.
Wie hoch sind die monatlichen Kosten der Familie Koch, wenn davon ausgegangen wird, dass die jährlichen Kosten gleichmäßig auf zwölf Monate verteilt werden?
- 4
Herr Schmidt kauft ein Auto zum Preis von 13750 € und lässt diese Summe vom Autohändler finanzieren. Nach einem Jahr hat Herr Schmidt 15331,25 € gezahlt und den Kredit damit vollständig getilgt.
Wie hoch war der Zinssatz?
% - 5
Für ein Darlehen von 33000 € mussten bei einem jährlichen Zinssatz von 8% insgesamt 9240 € an Zinsen gezahlt werden.
Nach welcher Zeit wurde das Darlehen abgelöst?
Monate - 6
Ein Sparer erhält für sein Kapital von 42500 € bei einem jährlichen Zinssatz von 6,5% eine Zinsauszahlung in Höhe von 552,50 €.
Wie lange war das Kapital angelegt?
Tage - 7
Das Haus der Familie Müller ist mit einer Hypothek belastet. Familie Müller zahlt bei einem jährlichen Zinssatz von 8,5 % monatlich 637,50 € Zinsen.
Wie hoch ist die Hypothek?
€ - 8
Ein Kapital von 22 500 € wird zu einem jährlichen Zinssatz von 7,5% angelegt.
Wie hoch ist der Zins nach 9 Monaten und 10 Tagen?
€ - 9
36000 Euro werden am 1. Februar auf ein Konto zu 5,5% Jahreszins einbezahlt. Im Verlaufe des Jahres wurde der Zinssatz auf 5% gesenkt. Am Ende des Jahres konnten 1762,5 Euro an Zinsen kassiert werden. Nach wie vielen Monaten fand die Zinssenkung statt?
Monate - 10
Ein Kleinwagen kostet 15600 Euro, wenn er bar bezahlt wird. Das Auto kann auch in zwei Raten zu 8000 Euro bezahlt werden, wobei die erste Rate sofort und die zweite nach einem halben Jahr fällig ist. Wie hoch ist der Jahreszinssatz, den der Verkäufer bei diesem Abzahlungsgeschäft verlangt?
% - 11
Welche Summe muss man heute zu 6% Jahreszins anlegen, um in einem halben Jahr an Kapital und Zinsen 10 000 Euro zu besitzen? Runde auf ganze Euro.
€ - 12
Zwei Banken liefern sich einen Wettbewerb um die Gunst der Kunden.
Bank A sagt: "Bei uns bekommen Sie 8% Zins auf ihre Spareinlagen."
Bank B sagt: "Bei uns bekommen Sie zweimal im Jahr, nämlich einmal Ende
Juni und einmal Ende Dezember, 4% Zins auf Ihrem Konto gutgeschrieben."
Begründe rechnerisch, bei welcher Bank man als Kunde besser fährt.
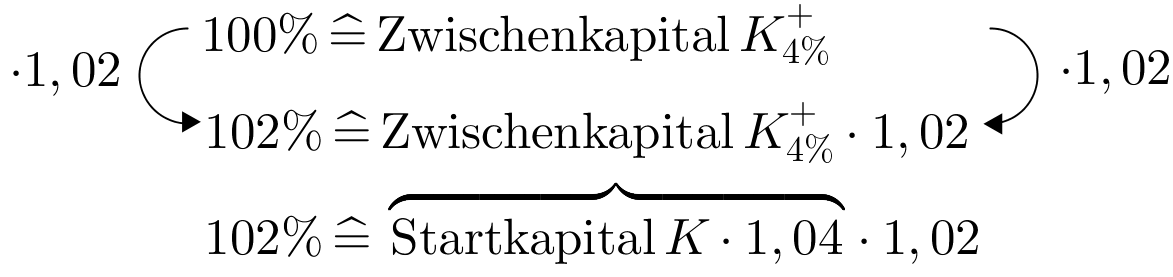
- 13
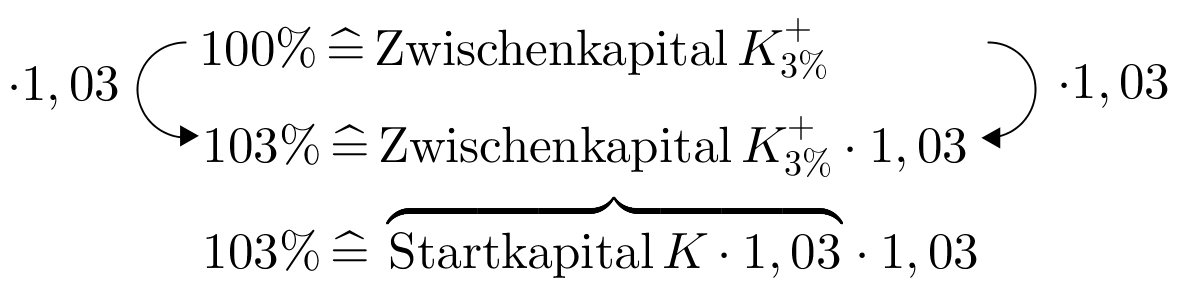
Herr Steger hat ein Kapital auf 5 Jahre zu 6% festgelegt (ohne Zinseszins!).
Wie hoch war das Kapital, wenn Herrn Steger nach 5 Jahren 45500 € ausgezahlt wurden?
€ - 14
Was ist günstiger: Verzinsung eines Bank-Guthabens zwei Jahre lang mit je 3% (mit Zinsenzins d.h. nach einem Jahr wird der Zins zum Guthaben dazugezählt und im zweiten Jahr mitverzinst), oder 4% im ersten Jahr und 2% im zweiten Jahr (ebenfalls mit Zinseszins)?
- 15
Der schwedische Erfinder Alfred Nobel stiftete in seinem Testament ein großes Vermögen, von dessen Zinsen jährlich die Nobelpreise der Physik, Chemie, Medizin und Literatur sowie der Friedensnobelpreis finanziert werden. Das Vermögen der Nobelstiftung belief sich im Jahr 2011 auf ca. 3 Milliarden schwedische Kronen (SEK). Der Jahreszins beträgt ca. 4%. Im Jahr 2011 werden 50 Millionen schwedische Kronen an Preisgeldern ausgezahlt. Der Rest der Zinsen wird für Organisatorisches und die Feierlichkeiten zur Nobelpreisverleihung verwendet. Wieviel Geld ist das?
- 16
Stelle dir vor, es hätte jemand für dich vor 2000 Jahren einen Euro zu einem Jahreszinssatz von 2% angelegt. Wie viel Geld hättest du dann heute?
- 17
Karl muss sich ein neues Sofa kaufen. Da er die 750 € für das Sofa noch nicht hat, will er es sich mithilfe einer Finanzierung kaufen. In der Werbung hört er von zwei Angeboten.
Beim ersten Angebot ist es eine 0% Finanzierung. Karl müsste dem Möbelhaus in einem Jahr 750 € zahlen. Beim zweiten Angebot will das Möbelhaus in einem Jahr 700 € und verlangt zusätzlich 5% Zinsen.

Welches der Angebote ist für Karl günstiger?
- 18
Jannick bekommt auf sein Konto 1% Zinsen. Da die Bank viele Gewinne einfahren konnte, erhöht sie seinen Zinssatz um 0,2 Prozentpunkte.
Wie hoch ist Jannicks neuer Zinssatz?
%Wie hoch wäre Jannicks Zinssatz, wenn er um 0,2 Prozent erhöht worden wäre?
%
- 19
Überlege dir, wann es keinen Unterschied macht, ob man von Veränderung in Prozent oder Prozentpunkten spricht.
- 20
Im Jahr 2000 hat Frau Schuhmacher ein Sparkonto mit 5000 € mit einen Zinssatz von 1 % pro Jahr angelegt. Noch im gleichen Jahr hebt Frau Schumacher jedoch 10 € ab. Im Jahr darauf schon 20 € und in jedem weiteren Jahr wieder 10 € mehr. Die Verzinsung erfolgt jeweils erst nach der Abhebung. Berechne für die ersten 10 Jahre den Kontostand nach der Verzinsung. Gibt es ein Maximum (oder Minimum) des Kontostands? Erkläre warum. Wie wird sich der Kontostand weiterentwickeln?
- 21
Der kleine Jakob bekam zur Geburt im Jahr 2001 von seiner Oma ein Sparbuch über geschenkt. Bei der Euro-Umstellung füllte die Oma den entstehenden „krummen“ Geldbetrag durch eine Einzahlung auf auf. Ansonsten wurde kein Geld mehr eingezahlt. Das Guthaben auf Jakobs Konto hat sich aber trotzdem etwas vermehrt, weil er am Ende jedes Jahres von der Bank Zinsen bekommt.
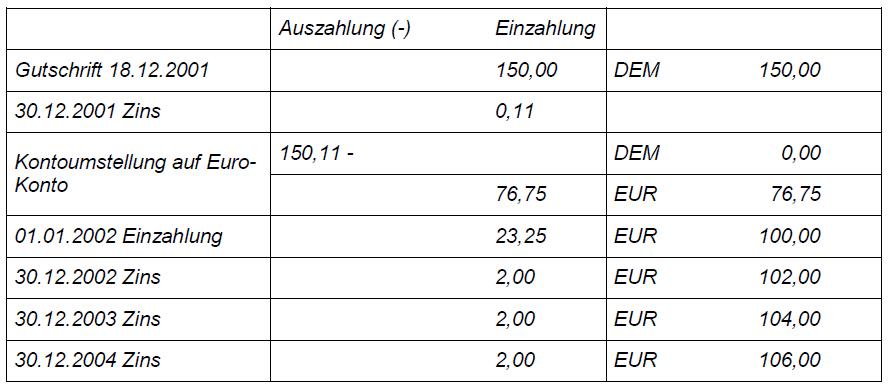
Wie viel Prozent Zinsen hat Jakob für sein Guthaben im Jahr 2002 bekommen? (Man sagt hierzu auch: „Welchen Zinssatz hat er im Jahr bekommen?“)
%War der Zinssatz im Jahr 2004 höher oder niedriger als im Jahr 2002? Begründe deine Antwort.
Die Zinsen für das Jahr 2005 sind noch nicht im Sparbuch eingetragen. Der Zinssatz beträgt . Berechne Jakobs Guthaben zum 30.12.2005.
€
- 22
Deine Eltern haben für dich auf der Bank Festgeld bei einem Zinssatz von angelegt. Nach einem Jahr werden dir auf deinem Sparbuch dafür Zinsen gutgeschrieben.
Berechne, wie viel Geld deine Eltern für dich angelegt haben.
€Bei der Berechnung von Zinsen legt die Bank ein sog. „Bankjahr“ zugrunde. Ein „Bankjahr“ besteht aus Monaten mit einheitlich je Tagen, also aus insgesamt Tagen. Berechne, wie viel Zinsen du in Tagen erhältst.
€
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?