1 Übersicht
Ziel dieses Kurses ist es, einen Überblick zur möglichen Vorgehensweise beim Finden von Nullstellen von Polynomfunktionen zu geben.
Inhalte
Erarbeitung der Linearfaktordarstellung
Methoden der Nullstellenberechnung
Termumformungen
Ausklammern von Faktoren
Lösen mithilfe der Polynomdivision
Lösen durch Substitution
Vorwissen
Funktionsbegriff
Polynomfunktion
Definition einer Nullstelle
Berechnung von Nullstellen bei linearen und quadratischen Funktionen
2 Nullstellen
Eine Nullstelle einer Funktion ist der -Wert eines Schnittpunktes vom Graphen von mit der x-Achse.
Das sind also gerade die -Werte, an denen ist.
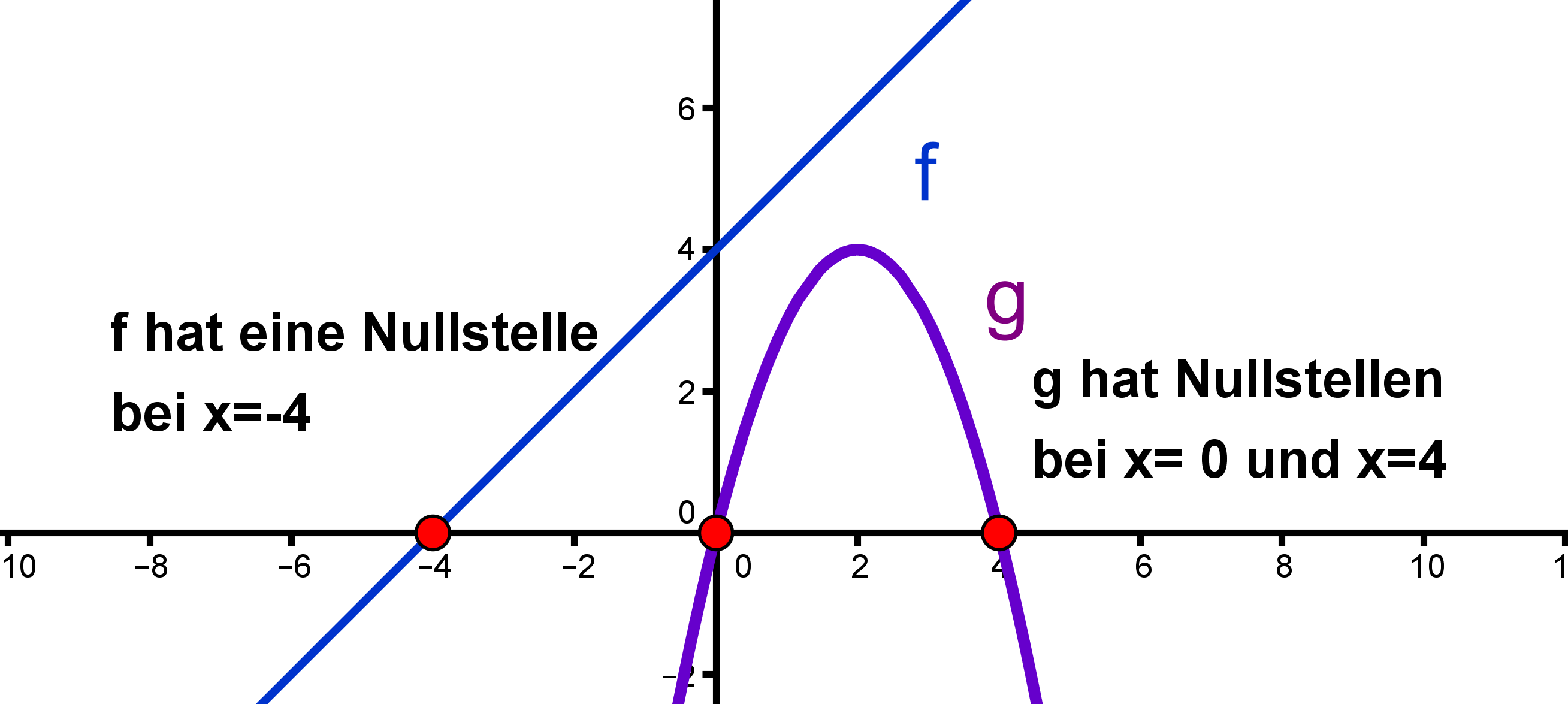
Hier sind die Nullstelle(n) der linearen Funktion f mit und der quadratischen Funktion g mit eingezeichnet.
Wie du Nullstellen von linearen und quadratischen Funktionen berechnest, wird dir im Artikel Nullstellen berechnen gezeigt. Ansonsten gehe einfach zur nächsten Kursseite.
3 Linearfaktordarstellung (1|3)
Bei linearen und quadratischen Funktionen ist die Berechnung mithilfe einer Termumformung oder der quadratischen Lösungsformel (Mitternachtsformel) relativ gut machbar.
Das wirft die Frage auf, ob es für Polynomfunktionen höheren Grades (zum Beispiel ) im Allgemeinen auch eine solche Formel zur Bestimmung von (reellen) Nullstellen gibt.
Gibt es eine allgemeine "Nullstellenformel" für jede Polynomfunktion?
Diese Formel existiert leider nicht. Es gibt aber ein gutes Hilfsmittel, um die Nullstellen von Polynomfunktionen zu finden. Dieses erarbeiten wir uns mithilfe eines Beispiels auf den nächsten Seiten.
Linearfaktor
Die Funktion ist eine Funktion dritten Grades. Sie ist jedoch etwas anders dargestellt, als unsere gewöhnliche Form Polynomfunktionen aufzuschreiben. (Die allgemeine Darstellung der Funktion wäre .)
Die etwas merkwürdigere erste Darstellung hat aber den Vorteil, dass man am sogenannten Linearfaktor ganz einfach die Nullstelle ablesen kann. Damit wissen wir auch, dass eine Nullstelle von ist.
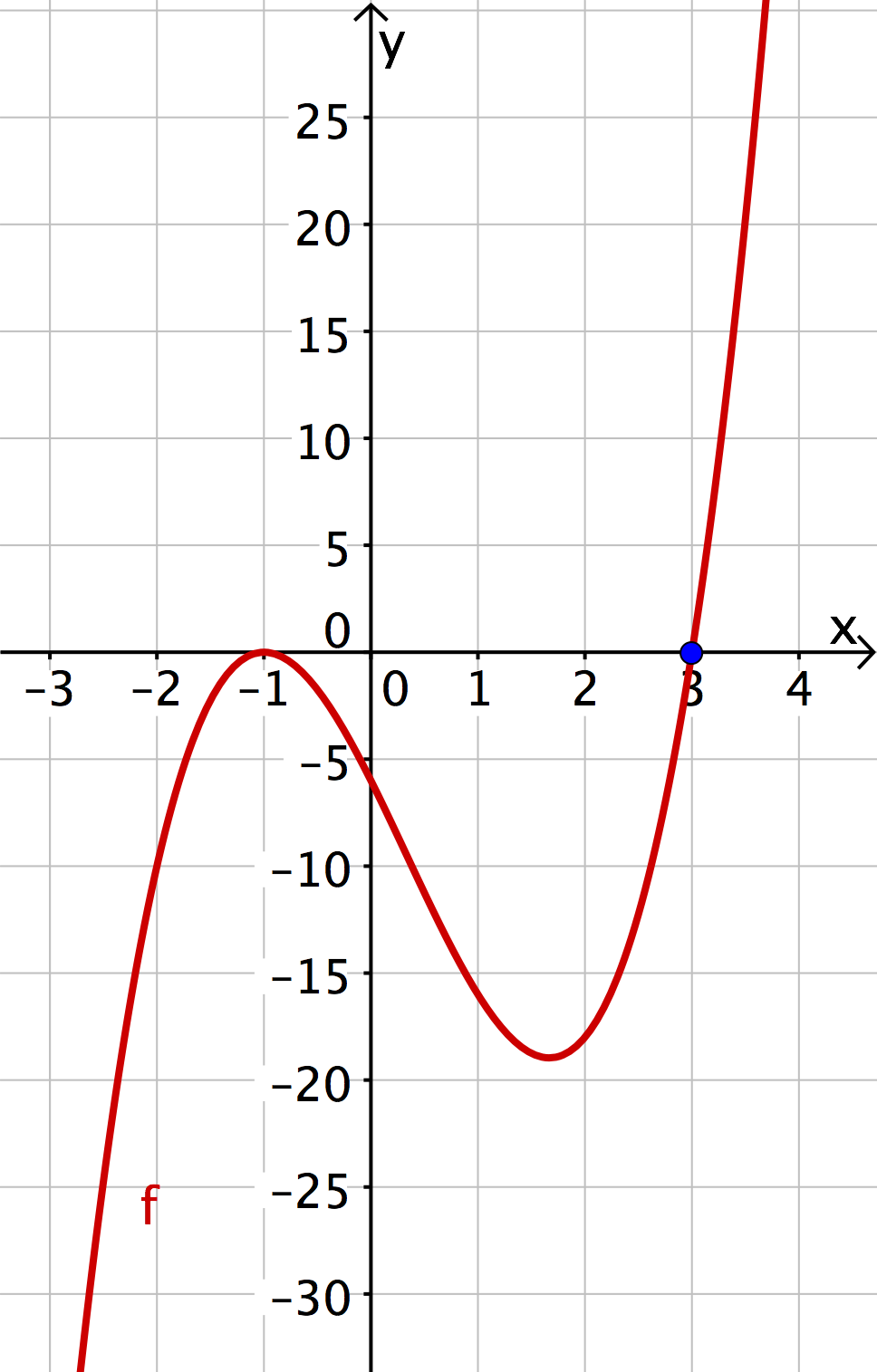
Ein Linearfaktor hat im Allgemeinen die Form und wird genau dann , wenn man für die Zahl einsetzt ().
Dabei kann auch negativ sein. So hat zum Beispiel der Linearfaktor die Nullstelle .
4 Linearfaktordarstellung (2|3)
Linearfaktordarstellung
Manchmal kann man eine Polynomfunktion komplett in Linearfaktoren aufspalten.
Aus unserer vorherigen Funktion wird dann zum Beispiel . (Wir benutzen dabei die erste binomische Formel.)
Diese komplett zerlegte Form hat einen besonderen Namen…
Diese Form nennt man die Linearfaktordarstellung von .
Dabei können durchaus mehrere N gleich sein. Dies ist zum Beispiel bei unserer Funktion der Fall.
Störe dich nicht an einem möglichen im Linearfaktor zum Beispiel bei . Dies kannst du ganz einfach in die Form bringen.
Der Faktor ist hier immer der Koeffizient der Potenz, die den Grad angibt (also die mit dem höchsten Exponenten). In unserem Beispiel ist die der Koeffizient von .
Zur besseren Übersicht lassen sich oft gleiche Linearfaktoren mithilfe einer Potenz zusammenfassen. Bei uns: .
Ablesen von Nullstellen
An der Darstellung lassen sich nun alle Nullstellen ablesen:
An dem Linearfaktor lesen wir die Nullstelle ab; an den beiden Linearfaktoren lesen wir die Nullstelle ab.
Wie du siehst, hat die Linearfaktordarstellung einige Vorteile gegenüber der allgemeinen Darstellung .
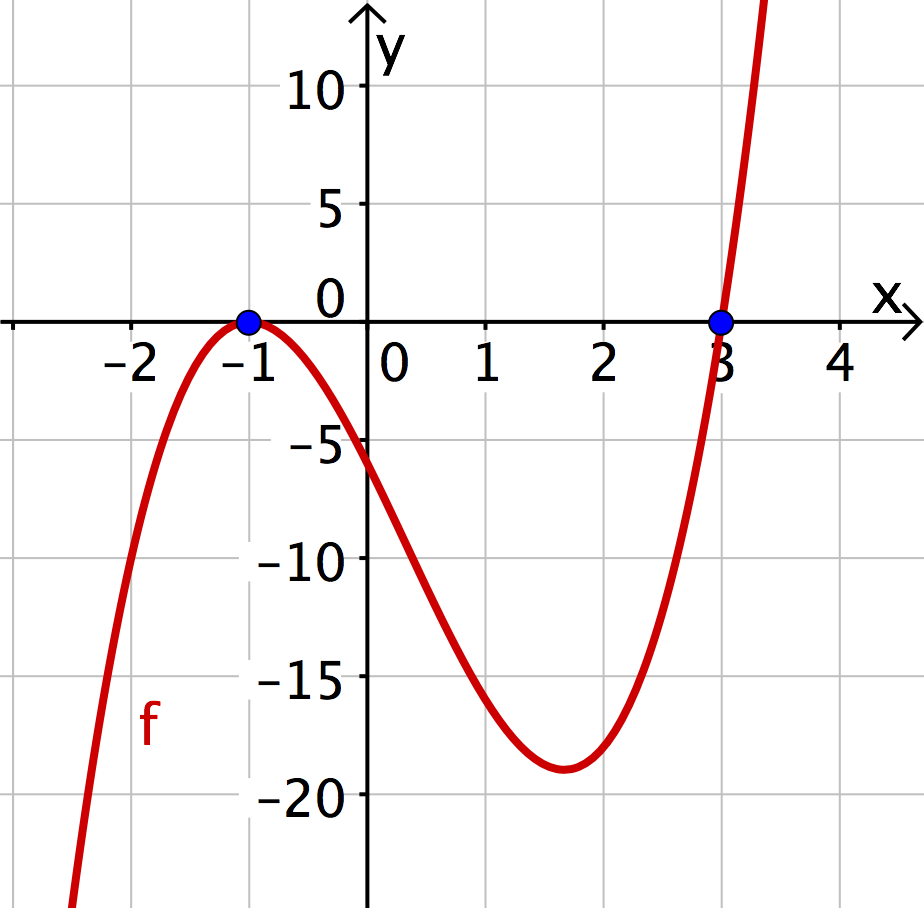
5 Linearfaktordarstellung (3|3)
Unsere vorherige Beispielfunktion war eine Polynomfunktion vom Grad und konnte in die Linearfaktoren (einmal) und (zweimal) zerlegt werden. ließ sich insgesamt also in drei Linearfaktoren aufspalten.
Leider können nicht alle Polynomfunktionen komplett in Linearfaktoren zerlegt werden. So hat zum Beispiel die Funktion keine reellen Nullstellen und kann nicht als Produkt von Linearfaktoren geschrieben werden. Bleibt beim Aufspalten einer Polynomfunktion in Linearfaktoren ein solches Restglied übrig, so ist eine komplette Zerlegung in Linearfaktoren nicht möglich.
Für Polynomfunktionen, bei denen eine solche Darstellung nicht möglich ist, gibt es eine Darstellung, die der Linearfaktordarstellung ähnlich ist:
wobei das Restglied wieder ein Polynom ist, welches keine reellen Nullstellen besitzt.
Diese Darstellung ist bei jeder Polynomfunktion möglich und ist zum Ablesen ihrer Nullstellen genauso praktisch.
Eine Folgerung der Linearfaktordarstellung
Eine Polynomfunktion vom Grad kann maximal in Linearfaktoren zerlegt werden. Wäre sie ein Produkt von mehr als Linearfaktoren, so hätte die Funktion ausmultipliziert einen höheren Grad.
Damit gilt auch:
6 Übersicht - Berechnungsmethoden
Die Linearfaktordarstellung bzw. die Darstellung mit Linearfaktoren und einem Restglied ermöglicht es uns, sehr einfach die Nullstellen einer Polynomfunktion abzulesen.
Es kann aber etwas schwieriger sein, den Funktionsterm in diese Darstellung umzuwandeln.
Auf den nächsten Kursseiten lernst du ein paar Methoden kennen, mit denen du entweder die Nullstellen direkt bestimmen oder den Funktionsterm in eine Darstellung mit Linearfaktoren umformen kannst.
Diese sind…
Termumformungen
Ausklammern von Faktoren
Lösen mithilfe der Polynomdivision
Lösen durch Substitution
Zuerst wiederholen wir aber ein paar nützliche Hilfestellungen. Gehe dazu auf die nächste Kursseite.
7 0. Hilfestellungen
Auf unserem Weg zur Berechnung von Nullstellen gibt es ein paar Formeln und "Tricks", die sehr nützlich sein können. Manche davon wirst du schon kennen, manche können auch neu sein. Auf alle Fälle solltest du dir die folgenden Tricks merken.
Quadratische Lösungsformel (Mitternachtsformel)
Diese Formel liefert uns die Nullstellen einer beliebigen quadratischen Funktion (wenn es sie gibt!). Für eine quadratische Funktion mit liefert die quadratische Lösungsformel die Nullstellen:
Das Zeichen "" sagt uns, dass es zwei Fälle zu unterscheiden gibt. Die erste Nullstelle ist gegeben durch die obige Formel, wenn man statt "" nur ein "" nimmt. Ersetzt man dagegen "" durch ein "", so kann sich eine weitere Nullstelle ergeben.
Diese Formel sagt uns auch, wann die Funktion keine Nullstellen hat. Das ist der Fall, wenn unter der Wurzel in der Formel eine negative Zahl steht.
Mehr zu dieser Formel findest du im Artikel Mitternachtsformel. Für den Spezialfall, das ist, gibt es auch eine etwas einfachere Formel, die pq-Formel. Es genügt aber, die quadratische Lösungsformel zu kennen, da sie auch die Fälle, wenn ungleich ist, abdeckt.
Die binomischen Formeln
Es gibt drei binomische Formeln. Die ersten zwei Formeln sagen uns, wie die zweite Potenz eines Linearfaktors aussieht. Linearfaktoren sind wichtige Informationen bei der Nullstellensuche, nicht vergessen ;). Die dritte ist ein bisschen anders, aber genauso hilfreich.
Erste binomische Formel
Für eine beliebige positive Zahl und eine beliebige Zahl gilt:
Oft wollen wir diese Formel von "rechts nach links" benutzen, da wir oftmals Terme wie auf der rechten Seite gegeben haben. Die linke Seite ist ja ein Linearfaktor "hoch ". Damit ist die linke Seite hilfreicher, um die Nullstelle eines Polynoms zu finden.
Zweite binomische Formel
Für eine beliebige positive Zahl und eine beliebige Zahl gilt:
Aufgepasst! Auch hier verlangen wir, dass positiv ist. Nur diesmal subtrahieren wir diese Zahl von . Auch diese Formel lesen wir gerne rückwärts.
Dritte binomische Formel
Für eine beliebige positive Zahl und eine beliebige Zahl gilt:
Diese Formel ist ziemlich mächtig. Wenn wir zum Beispiel den Term sehen, müssen wir nur erkennen, dass nichts anderes als ist. Die dritte binomische Formel sagt uns dann, dass genau und die Nullstellen von sind.
8 1. Termumformungen
Termumformungen sind generell gut, wenn wir die Nullstellen einer ganzrationalen Funktion suchen, die die Summe einer Potenzfunktion und einer Zahl ist.
Beispiele für Vorschriften solcher Funktionen sind:
Berechnen wir doch mal die Nullstellen der ersten Funktion . Richtig erkannt, ist ja eine quadratische Funktion. Sogar eine "recht einfache", denn im Allgemeinen taucht bei einer quadratischen Funktion auch ein -Term auf, was bei unserem nicht der Fall ist.
Ihre Nullstellen mit der quadratischen Lösungsformel (oder der pq-Formel) zu suchen wäre also sowas wie mit Kanonen auf Enten zu schießen. Außerdem geht es wesentlich schneller.
Fangen wir doch mal einfach an, indem wir den Term gleich null setzen.
Bringe die auf die rechte Seite
Jetzt bleibt nur noch die Wurzel zu ziehen
Wir haben also nur zwei Umformungen gebraucht, um die Nullstellen von zu finden. Außerdem können wir an diesem Beispiel genau sehen, wann so eine quadratische Funktion keine Nullstellen hat.
Wir hätten in der dritten Zeile nicht die (zweite) Wurzel ziehen können, wenn auf der rechten Seite eine negative Zahl gestanden hätte.
Generell muss man beim Ziehen gerader Wurzeln (also zweite, vierte, sechste…) vorsichtig sein. Überprüfe immer vor dem Wurzelziehen, ob unter der Wurzel eine positive oder eine negative Zahl stehen wird! Ungerade Wurzeln kann man immer ziehen. Sie haben alle genau eine reelle Lösung.
9 2. Ausklammern von Faktoren (1|2)
Schaue dir die folgenden Funktionsterme kurz an.
Auf den ersten Blick scheinen sie sehr kompliziert zu sein. Lass dich nicht abschrecken, denn jetzt lernst du, wie du sie in eine schönere Form bringen kannst!
Werfen wir zuerst einen Blick auf .
Es fällt doch auf, dass alle Summanden -Terme sind. Es gibt also kein konstantes Glied. Da die kleinste Potenz von ist, die in der Funktionsvorschrift von vorkommt, können wir ausklammern.
Schon sieht viel besser aus. An dem Faktor können wir sofort eine Nullstelle bei ablesen.
Der Faktor in der Klammer ist die Vorschrift einer quadratischen Funktion. Für solche Funktionen kennen wir die quadratische Lösungsformel, um ihre Nullstellen zu finden.
Indem wir ausklammern, lässt sich also als das Produkt von zwei einfacheren Funktionen schreiben. Von diesen können wir die Nullstellen gut berechnen (oder sogar ablesen).
Wir können somit alle Nullstellen von wissen. Denn damit ein Produkt null wird, muss mindestens einer der Faktoren auch gleich null sein.
Der Faktor hat eine Nullstelle bei . Also hat auch bei eine Nullstelle. Der Faktor ist ein quadratischer Term. Seine Nullstellen können wir mit der quadratischen Lösungsformel berechnen. Sie sind und
Damit lauten alle Nullstellen von : und .
Bei handelt es sich um eine sogenannte dreifache Nullstelle. In einem weiteren Kurs erfahren wir, was das genau bedeutet.
Taucht im Funktionsterm kein konstantes Glied auf, so können wir die kleinste Potenz von ausklammern.
Fragst du dich, ob du sowas auch für die Funktion machen kannst? Dann gehe auf die nächste Kursseite und finde es heraus!
10 2. Ausklammern von Faktoren (2|2)
Hier nochmal die Vorschrift von
Ganz am Ende dieses Ausdrucks steht die Konstante . Wir können also keine Potenz von ausklammern. Fällt uns was besseres ein?
Selbstverständlich!
Wie lesen wir die Vorschrift von geschickter?
Es gibt einen Trick, den man ganz leicht anwenden kann, um kompliziertere Funktionsterme (wie den von ) zu verstehen. Wir sind uns sicher einig, dass der Teil besonders schlimm aussieht. Denken wir ihn uns also für eine Minute weg.
hat dann die Vorschrift schlimmer Teil
Statt "x minus Eins mal x plus Eins zum Quadrat minus Eins plus x minus Eins", haben wir jetzt: "x minus Eins mal schlimmer Teil plus x minus Eins". Das liest sich doch wesentlich leichter, nicht wahr?
Diese Art zu schreiben ist wesentlich angenehmer, als der Term mit dem wir angefangen hatten. Jetzt müssen wir wieder den "schlimmen Teil" in diese neue Form einsetzen und schauen, was wir dadurch gewonnen haben.
schlimmer Teil
Ist diese letzte Form etwa nicht wunderschön? Die Funktion ist also doch gar nicht so schlimm, wie wir uns gedacht hatten. Schaue dir unsere Überlegungen und unser Vorgehen für noch einmal an.
Was du auf jeden Fall von dieser Kursseite mitnehmen solltest: Komplizierte Terme denken wir uns erstmal weg. Sie können uns nicht abschrecken.
11 3. Lösen mithilfe der Polynomdivision (1|2)
Sind für eine Polynomfunktion vom Grad bereits Nullstellen bekannt (z.B. durch Raten), kannst du die Funktion durch eine Polynomdivision vereinfachen, sodass weitere Nullstellen leichter (z.B. mit der Mitternachtsformel) berechnet werden können.
Dabei kannst du folgendermaßen vorgehen:
1. Schritt: Errate eine Nullstelle durch systematisches Probieren.
2. Schritt: Teile die Ausgangsfunktion durch den zur Nullstelle gehörigen Linearfaktor .
3. Schritt: Überprüfe, ob du die Nullstellen des erhaltenen Polynoms mit einer dir bekannten Formel oder Methode bestimmen kannst. Ist dies nicht der Fall, wiederhole Schritt bis bei diesem Polynom.
4. Schritt: Ermittle die Nullstellen des erhaltenen Polynoms
Du kannst dir das alles noch nicht so richtig vorstellen?
Dann gehe auf die nächste Kursseite, dort findest du ein schrittweise erklärtes Beispiel!
12 3. Lösen mithilfe der Polynomdivision (2|2)
Beispiel
1. Schritt:
| ↓ | Versuche eine Nullstelle durch systematisches Probieren herauszufinden. Setze z.B. in ein. | ||
| ↓ | Setze z.B. in ein. | ||
Die Funktion hat an der Stelle eine Nullstelle.
2. Schritt:
Da , wissen wir, dass den dazugehörigen Linearfaktor besitzt.
Teile nun durch .
3. Schritt:
Die Funktion wird dann , sobald mindestens einer der Faktoren gleich ist. Da die Nullstelle bereits bekannt ist, kannst du die weiteren Nullstellen von bestimmen, indem du das erhaltene Polynom gleich setzt.
Da das Polynom die Form einer quadratischen Funktion hat, kannst du die Nullstellen mithilfe der Mitternachtsformel bestimmen.
4. Schritt:
| ↓ | Unter der Wurzel zusammenfassen. | ||
| ↓ | Berechne die Wurzel. | ||
Fall :
Fall :
13 4. Lösen durch Substitution (1|2)
Eine weitere Methode, Nullstellen von Polynomfunktionen vom Grad zu bestimmen, ist die sogenannte Substitutionsmethode.
Bei einer Substitution ersetzt man einen Term (bzw. Teile eines Terms) durch einen anderen, mit dem Ziel diesen in eine einfachere lösbare Form zu bringen.
Oft wird diese einfachere Form ein quadratischer Term sein, da wir für diesen mithilfe der quadratischen Lösungsformel die Nullstellen einfach berechnen können.
Betrachte zum Beispiel die Funktion mit . Wenn wir den Funktionsterm gleich null setzen, erhalten wir folgende Gleichung:
1. Geeignete Substitution finden und durchführen
Der Funktionsterm von besteht aus den Polynomgliedern und dem konstanten Glied . Beim ersten Glied fällt dir vielleicht ein, dass gerade ist. Das zweite Glied ist .
Ersetze nun alle im Funktionsterm durch eine neue Variable zum Beispiel (oder auch ). Warum dies besonders praktisch ist, wirst du gleich erkennen.
Schreibe also: "Substitution mit ".
Die Substitution bewirkt damit:
Damit haben wir jetzt das Polynomglied vierten Grades zu einem quadratischen Glied , und das quadratische Glied zu einem linearen Glied umgewandelt. Die Konstante bleibt dabei gleich - in ihr kommt ja kein vor.
Wir erhalten jetzt die quadratische Gleichung:
Durch das Ersetzen von durch die Variable ist es uns also gelungen, die erste Nullstellengleichung vierten Grades in eine quadratische Form zu bringen, die deutlich einfacher zu lösen ist.
2. Lösen der neuen Nullstellengleichung
Die Lösungen der neuen Gleichung kannst du zum Beispiel mit der quadratischen Lösungsformel finden.
Die Lösungen lauten (Bitte selber nachrechnen!):
und .
Wir dürfen nicht vergessen, dass wir substituiert hatten. Die Variable steht für . Noch haben wir also die Nullstellen von nicht.
3. Rücksubstituieren
Setzt man und wieder in die Substitutionsgleichung ein, so erhält man die zwei Gleichungen:
Damit eine Nullstelle von ist, muss es eine dieser Gleichungen erfüllen.
Mit den konkreten Zahlen…
Die Nullstellen von lauten also , , , .
Diesen Vorgang nennt man Rücksubstitution, da man die Substitution wieder "rückgängig macht".
14 4. Lösen durch Substitution (2|2)
Leider kann man die Substitutionsmethode nicht bei jeder Polynomfunktion anwenden!
Betrachte dazu die Funktion mit .
Wenn man wieder versucht durch zu ersetzen, erhält man leider keine neue Gleichung, die nur aus der neuen Variable besteht und quadratisch ist. Man findet für und keine schöne Darstellung wie im ersten Beispiel.
Ebenso bringt uns das Ersetzen von durch ein ebenfalls keine schöne Darstellung für und .
Die Substitution bewirkt:
Es scheint nur bei Polynomfunktionen zu funktionieren, die eine ähnliche Form zu der in unserem ersten Beispiel haben. Was diese Form ausmacht, erkennst du an den unteren drei Beispielen:
Man erkennt, dass Funktionsterme mit drei Polynomgliedern für die Substitution geeignet sind, wenn der höchste Exponent das Doppelte des anderen Exponenten ist und der dritte Term eine konstante Zahl ist.
Was du substituierst, ist deiner Kreativität überlassen. Das Ziel dabei ist, einen möglichst einfachen Term zu erhalten. Hier noch ein paar Beispiele für Substitutionen von verschiedenen Funktionstermen. Überlege zuerst, was du substituieren könntest, bevor du die Felder aufklappst.
15 Schema zur Nullstellenberechnung
Hier findest du als Zusammenfassung noch ein Schema, das du zur Berechnung von Nullstellen von Polynomfunktionen zu Hilfe ziehen kannst.
Klicke auf die Graphik, um sie in Vollbildversion zu sehen.
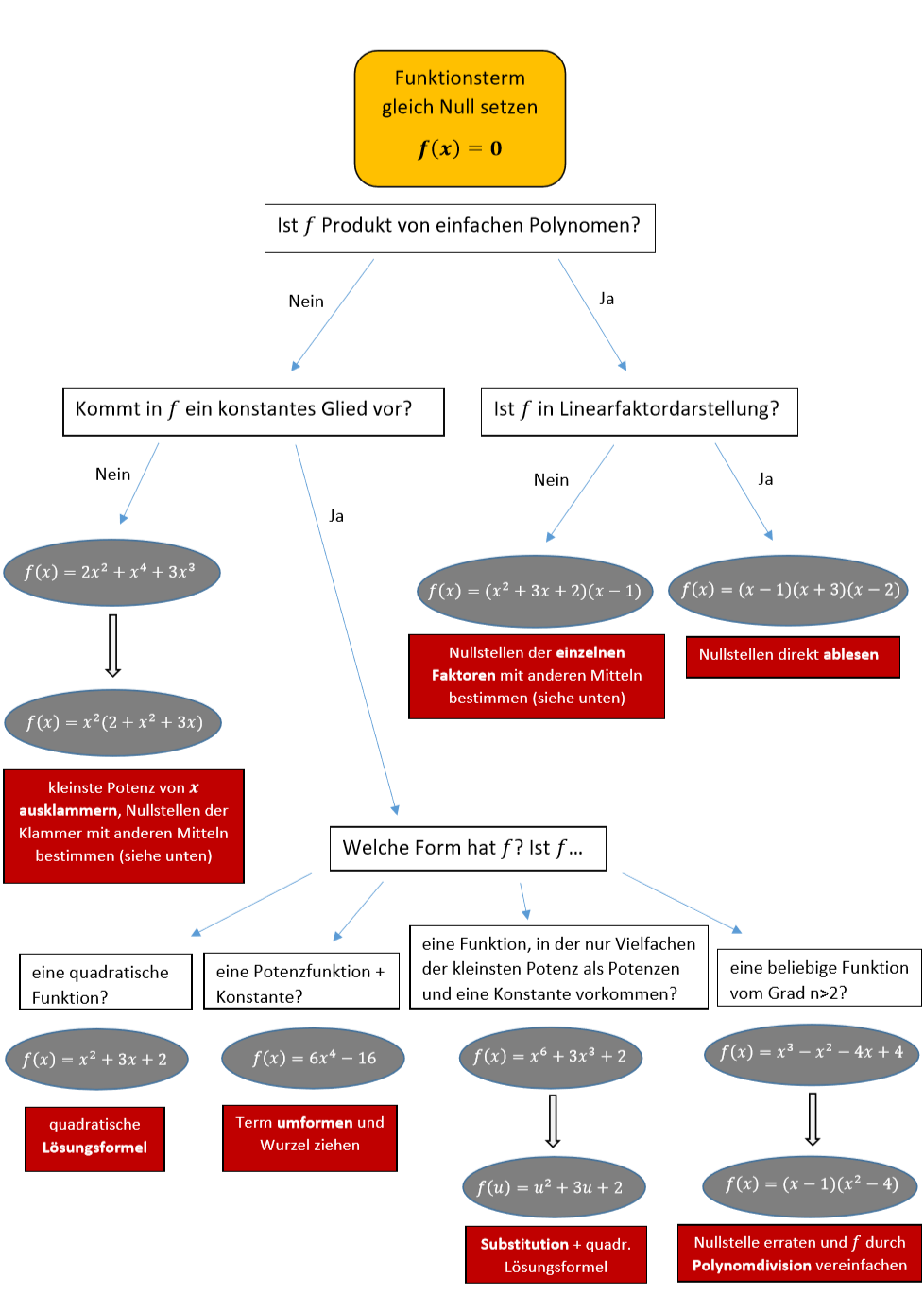
16 Aufgaben zur Nullstellenberechnung
Berechne die Nullstelle(n) der folgenden Funktionen.
a)
Laden
b)
Laden
c)
Laden
d)
Laden
e)
Laden
f)
Laden
g)
Laden
h)
Laden
i)
Laden
Falls du weitere Aufgaben bearbeiten möchtest, findest du sie im Aufgabenordner Aufgaben zur Bestimmung von Nullstellen.
Feedback
Damit wir unseren Kurs für die Zukunft verbessern können, würden wir uns sehr über ein Feedback von dir freuen. Es dauert auch nur 3 Minuten!
Klicke dazu auf diesen Link.
