2021
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Löse folgende Aufgaben.
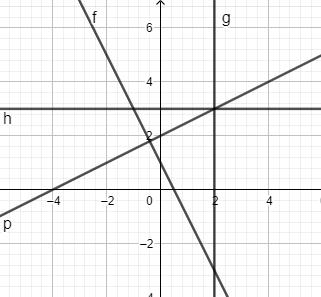
Gib die Gleichung der eingezeichneten Gerade g an.
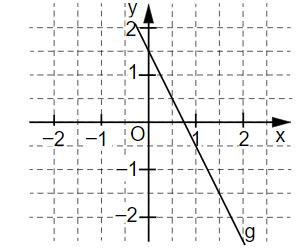
Der Punkt P(x|2) liegt auf der Gerade h mit der Gleichung y = 2x –4. Gib die fehlende x-Koordinate an.
P( |2)
Die Gerade f verläuft senkrecht zur Gerade h: y = 2x –4. Für den y-Achsenabschnitt der Gerade f gilt: t = 3,5. Gib die Gleichung der Gerade f an.
f: y=
- 2
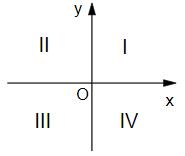
Gegeben sind vier Geradengleichungen. Kreuze an, welche zwei der zugehörigen Graphen durch den IV. Quadranten des Koordinatensystems verlaufen (siehe Skizze).
- 3
Gib die kleinste dreistellige natürliche Zahl mit der Quersumme 16 an.
- 4
Gib die Lösungsmenge L der Gleichung
(2 – x) ⋅ x = – (x² – 5) an.
L={ }
- 5
Löse die Klammer auf und fasse so weit wie möglich zusammen:
- 6
Berechne die Koordinaten des Punktes B (x | y), wenn gilt:
A (–1 | 2) und
B( | )
- 7
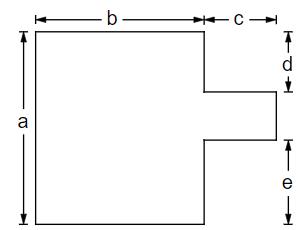
Die abgebildete Figur setzt sich aus zwei Rechtecken zusammen. Wie lässt sich der Flächeninhalt A der kompletten Figur beschreiben? Kreuze die beiden richtigen Möglichkeiten an.
- 8
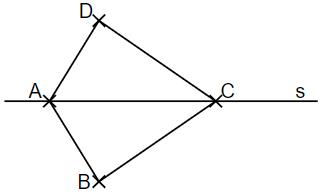
Das Drachenviereck ABCD mit cm hat einen Umfang u von 10 cm. Die Diagonale liegt auf der Symmetrieachse s. Vervollständige die Figur zum Drachenviereck ABCD.
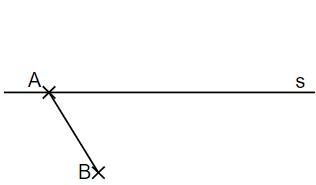
- 9
Für das Dreieck ABC (siehe Skizze) gilt:
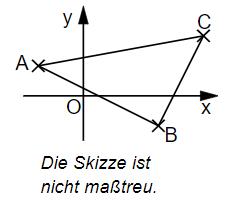
, ,
Berechne den Flächeninhalt A des Dreiecks ABC.
FE - 10
Ein Müslihersteller wirbt mit einer Sonderaktion: „Nur für kurze Zeit: 20% mehr Inhalt zum gleichen Preis!“ Wie viel Gramm Müsli befinden sich normalerweise (ohne Sonderaktion) in einer Packung?
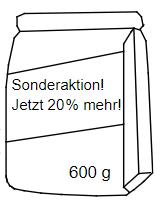
- 11
Ergänze den Nenner des folgenden Bruchterms, so dass dieser die Definitionsmenge
D = \ {0; –2} hat.
- 12
Gib die Lösungsmenge L der Bruchgleichung
mit D = \ {–3} an.
L={ }
- 13
Am Wahlfach Schulchor nehmen 50 Schülerinnen und Schüler teil, darunter sind viermal so viele Mädchen wie Jungen. Bei einem Auftritt des Chores sind 6 Mädchen und 4 Jungen krank, alle anderen singen mit. Kreuze an, welche Aussage bei diesem Auftritt zutrifft.
- 14
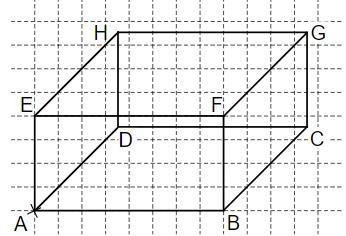
Der Quader ABCDEFGH hat die Grundfläche ABCD und folgende Maße: = 4 cm, = 5 cm und = 2 cm. Zeichne ein Schrägbild des Quaders mit dem Verzerrungsmaßstab und dem Verzerrungswinkel . Dabei soll auf der Schrägbildachse liegen.

- 15
Mert und Lilly üben das Werfen von Körben beim Basketball. Mert hat bei 27 Versuchen 9 Treffer erzielt. Lilly hat bei 21 Versuchen 7-mal in den Korb getroffen. Mert behauptet nun, dass er dabei die bessere Trefferquote hatte. Begründe mathematisch, dass Mert nicht Recht hat.
- 16
In einem Erlebnisaquarium kann man ein Haifisch-Becken durch einen gläsernen quaderförmigen Besuchertunnel mit 1 m Breite und 2 m Höhe komplett durchqueren(siehe Skizze). Nach Reinigungsarbeiten soll das leere Becken bis 0,5 m unter den Rand mit Wasser neu befüllt werden. Gib an, wie viele Kubikmeter Wasser dazu nötig sind.
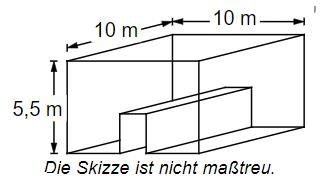
- 17
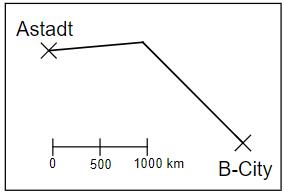
Die maßstabsgetreue Karte zeigt die Flugroute für den Flug von Astadt nach B-City. Das Flugzeug legt bei normalen Windverhältnissen pro Stunde durchschnittlich 500 km zurück. Wie viel Zeit muss man insgesamt einplanen, wenn sich die reine Flugzeit aufgrund von Gegenwind um 10 % erhöht und zur Flugzeit insgesamt noch 30 Minuten extra für den Start- und Landevorgang eingerechnet werden müssen?
Gib deinen Lösungsweg an.
- 18
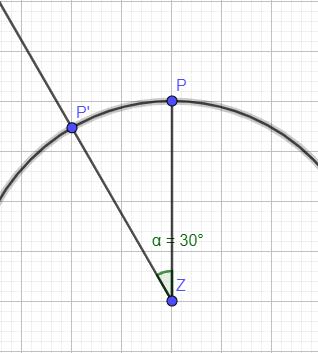
Der Punkt P soll durch Drehung um das Zentrum Z mit dem Maß des Drehwinkels α = 30° auf den Punkt abgebildet werden. Ermittle die Lage des Bildpunktes zeichnerisch.

- 19
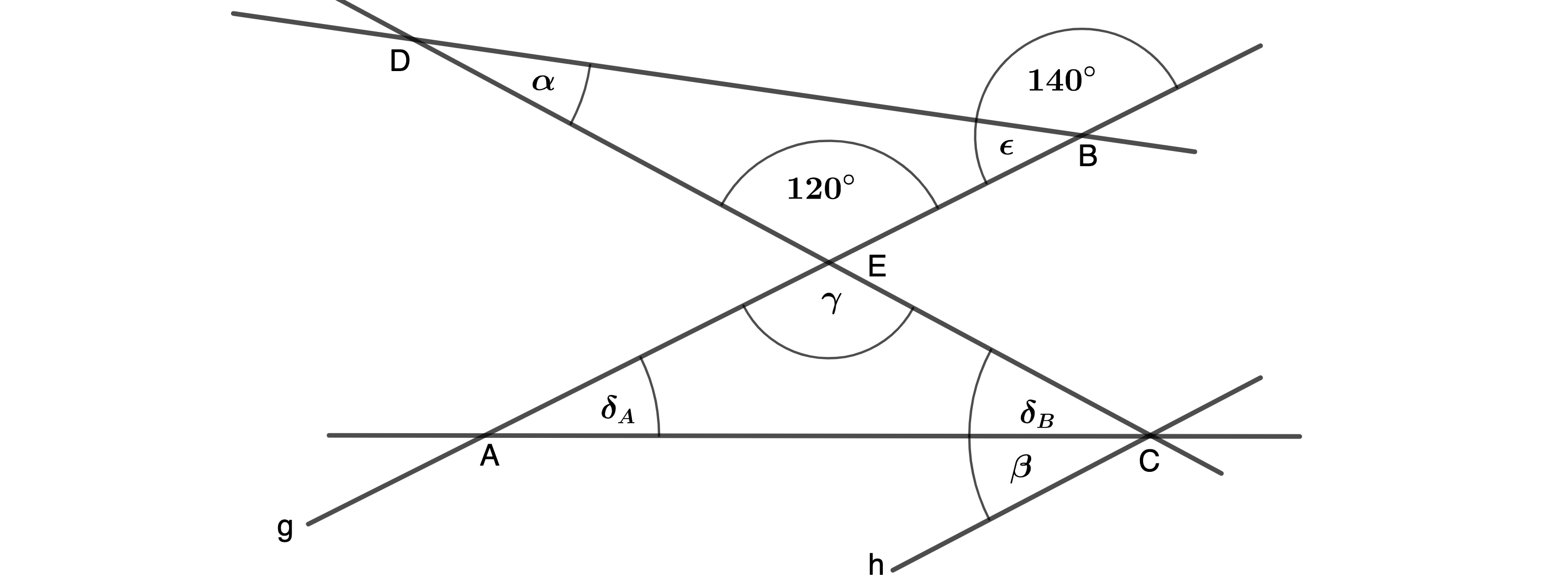
Gib die Winkelmaße α und β an. Es gilt: g || h und =
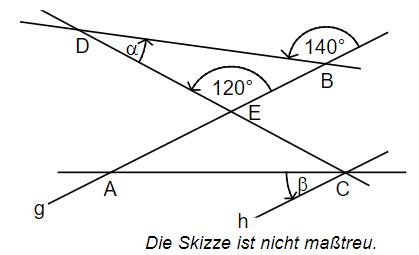
- 20
Die abgebildete Figur ist aus 12 deckungsgleichen Quadraten zusammengesetzt und hat einen Umfang u von 60 cm. Die Hälfte der Figur wurde grau eingefärbt. Gib den Flächeninhalt A der Fläche an, die gefärbt wurde.
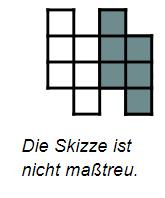 cm²
cm²
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?