Aufgaben zu linearen Funktionen, Nullstellen, Achsenschnittpunkten u.a.
Lerne mit diesen Übungsaufgaben lineare Funktionen zu skizzieren und die Schnittpunkte mit den Koordinatenachsen zu bestimmen!
- 1
Lies aus dem Graphen den y-Achsenabschnitt ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts mit der y-Achse , also .
Hast du eine Frage oder Feedback?
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Geraden mit der y-Achse betrachtest.
- 2
Lies aus dem Graphen die Nullstelle ab.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Die Nullstelle ist der x-Wert des Schnittpunkts der Geraden mit der x-Achse , also .
Hast du eine Frage oder Feedback?
Die Nullstelle bestimmst du, indem du den Schnittpunkt der Geraden mit der x-Achse betrachtest.
- 3
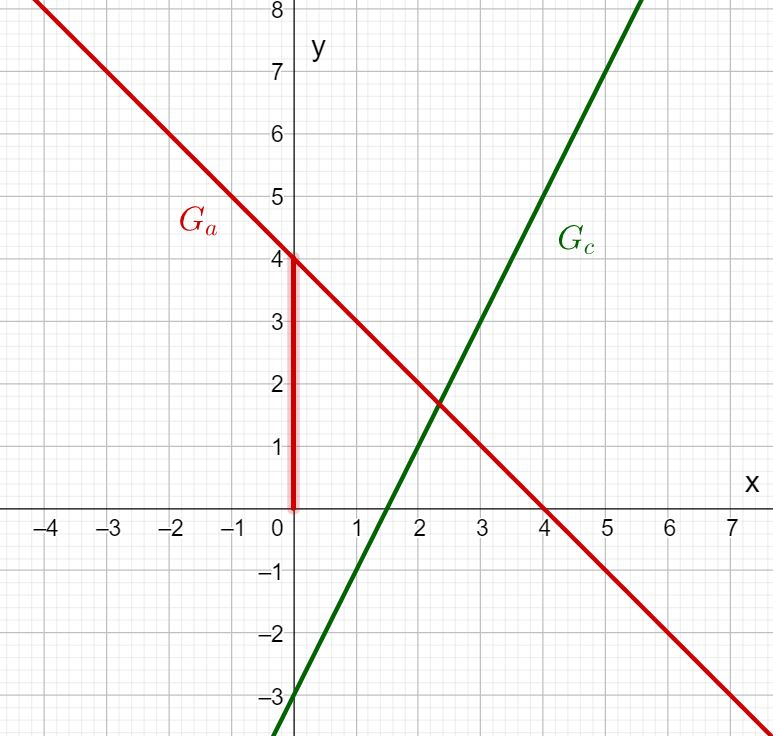
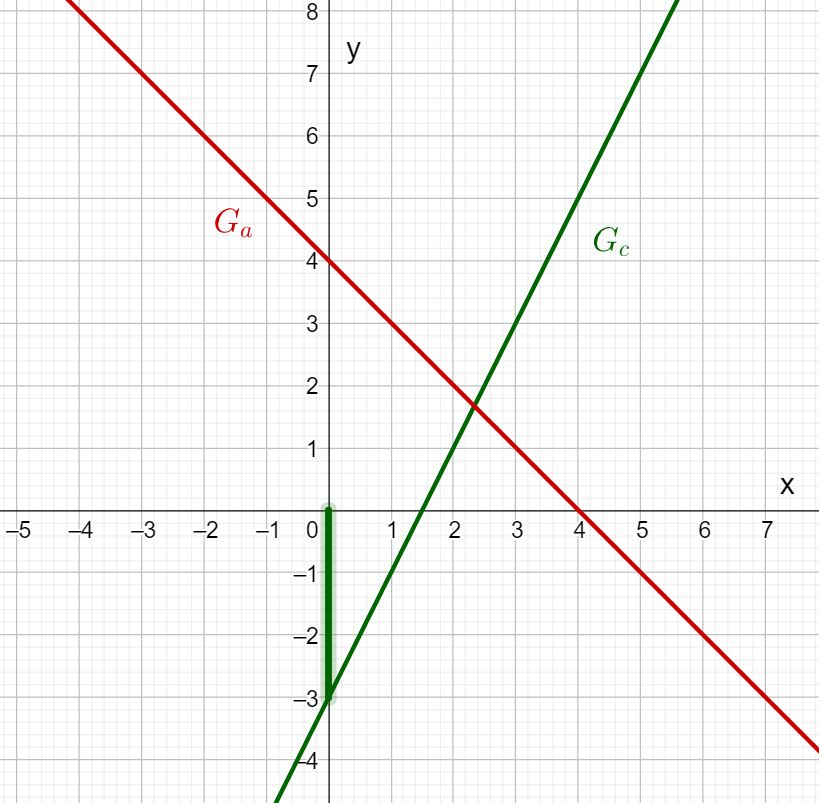
Betrachte die Graphen der Funktionen und . Lies den -Achsenabschnitt und die Steigung der Geraden ab und trage sie in die Felder ein! Kannst du daraus den Funktionsterm aufstellen?
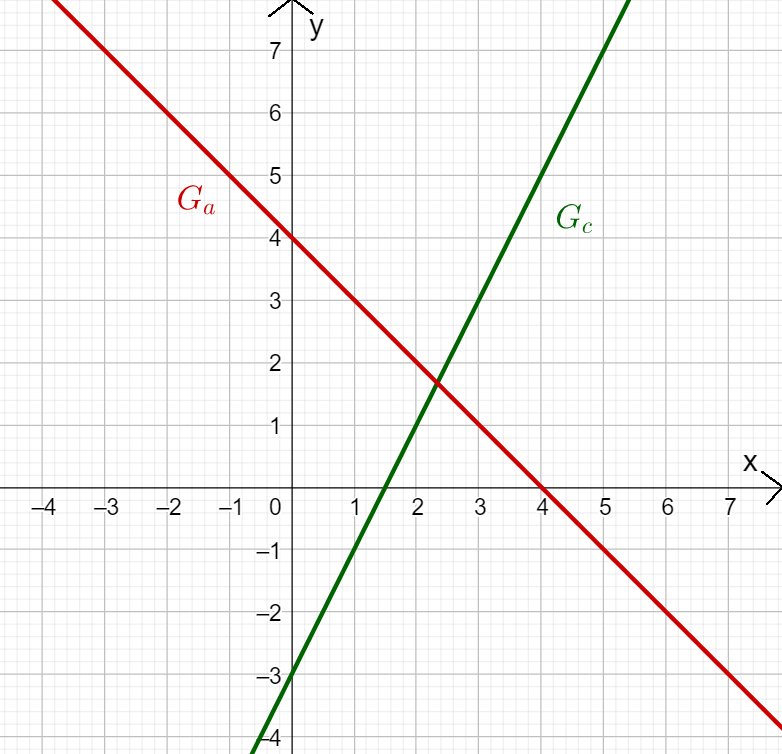
Welchen -Achsenabschnitt hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
-Achsenabschnitt bestimmen
Den -Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Gerade mit der -Achse betrachtest.
In diesem Fall:
Der -Achsenabschnitt ist der -Wert des Schnittpunkts , also .
Hast du eine Frage oder Feedback?
Achte darauf, wo die Gerade die y-Achse schneidet.
Bestimme dann den Schnittpunkt!
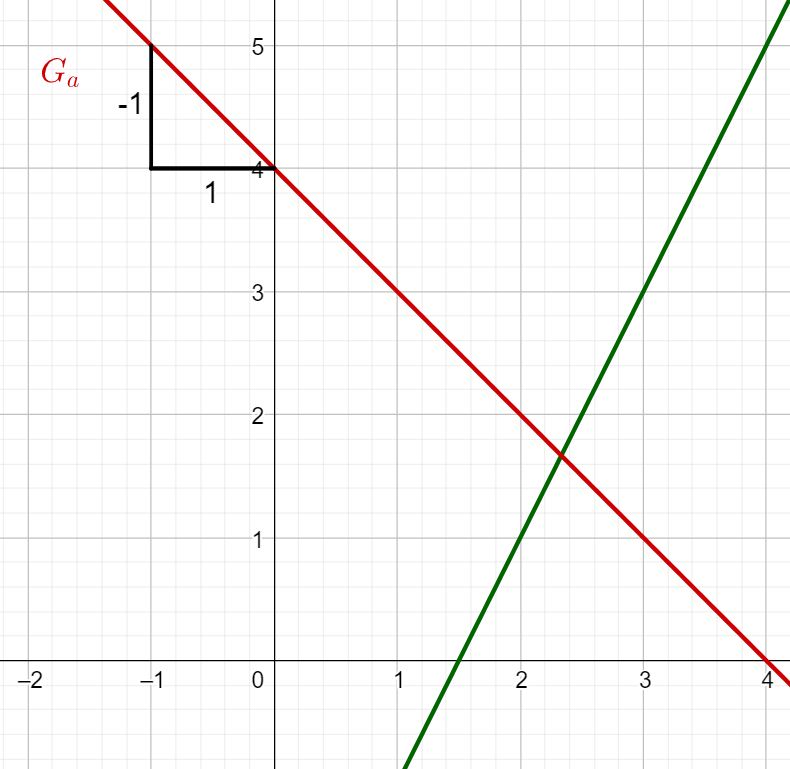
Welche Steigung hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Geraden
Steigung bestimmen
Die Steigung einer Geraden bestimmt man am einfachsten mithilfe eines Steigungsdreiecks.
Im Fall von :
Du kannst ablesen, dass du eine Längeneinheit nach unten und eine Längeneinheit nach rechts gehst.
Du erhältst für die Steigung:
Hast du eine Frage oder Feedback?
Kreiere dafür ein Steigungsdreieck (siehe unten).
Bestimme dann die Steigung.
Welchen Funktionsterm hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Funktionsterm aufstellen
Der Funktionsterm einer linearen Funktion hat die Form:
Dabei steht für die Steigung und für den -Achsenabschnitt.
Setzt du die Werte aus den vorigen Teilaufgaben ein erhältst du:
Vereinfacht ist das:
Die Funktionsgleichung von ist also:
.
Hast du eine Frage oder Feedback?
Schau dir das Grundwissen zu der linearen Funktion an.
Setze deine bisherigen Werte in die Funktion ein (siehe unten für eine ausführlichere Erklärung).
Welchen -Achsenabschnitt hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
-Achsenabschnitt bestimmen
Den -Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Gerade mit der -Achse betrachtest.
In diesem Fall:
Der -Achsenabschnitt von ist also .
Hast du eine Frage oder Feedback?
Achte darauf, wo die Gerade die y-Achse schneidet.
Bestimme dann den Schnittpunkt!
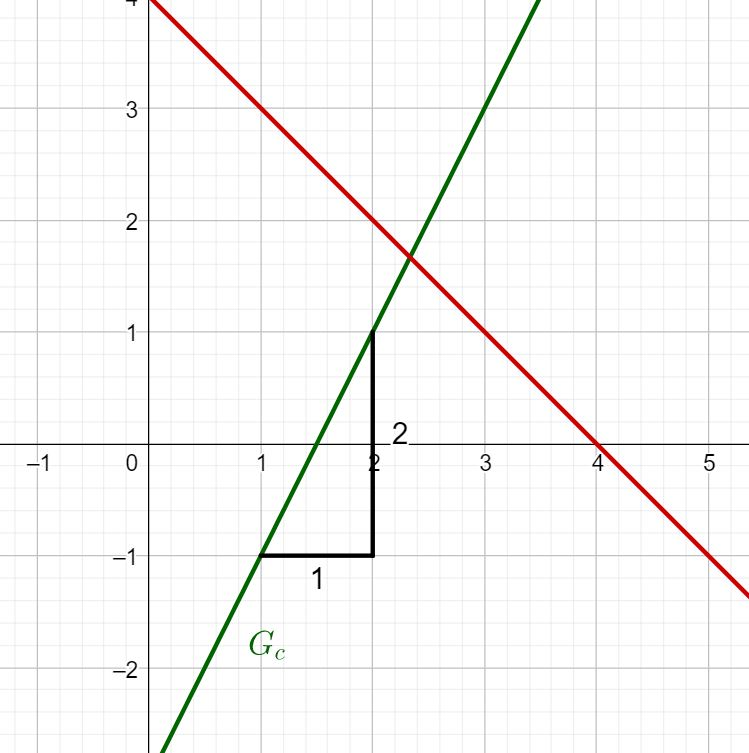
Welche Steigung hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Geraden
Steigung bestimmen
Die Steigung einer Geraden bestimmt man am einfachsten mithilfe eines Steigungsdreiecks.
Im Fall von :
Du kannst ablesen, dass du eine Längeneinheit nach rechts und zwei Längeneinheiten nach oben gehst.
Du erhältst für die Steigung:
Hast du eine Frage oder Feedback?
Kreiere dafür ein Steigungsdreieck (siehe unten).
Bestimme dann die Steigung.
Welchen Funktionsterm hat ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Funktionsterm aufstellen
Der Funktionsterm einer linearen Funktion hat die Form:
Dabei steht für die Steigung und für den -Achsenabschnitt.
Setzt du die Werte aus den vorigen Teilaufgaben ein erhältst du:
Die Funktionsgleichung von ist also:
Hast du eine Frage oder Feedback?
Schau dir das Grundwissen zur linearen Funktion an.
Setze deine bisherigen Werte in die Funktion ein (siehe unten für eine ausführlichere Erklärung).
- 4
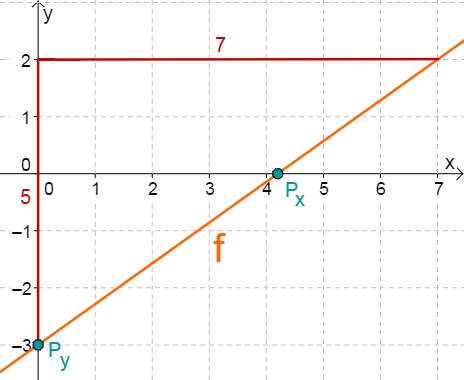
Zeichne die Graphen folgender Geraden mit dem Schnittpunkt mit der y-Achse und dem Steigungsdreieck. Berechne den Schnittpunkt mit der x-Achse und überprüfe das Ergebnis anhand des Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
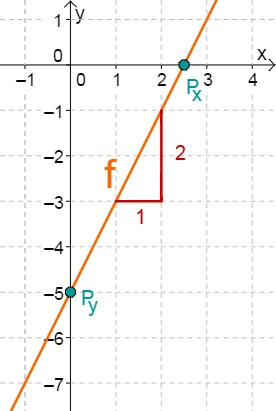
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
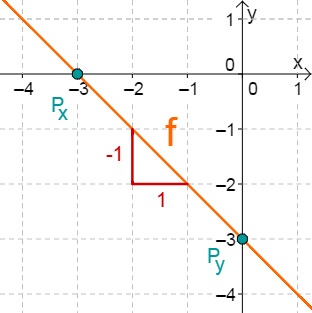
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
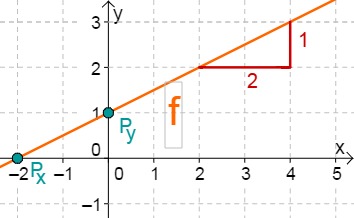
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
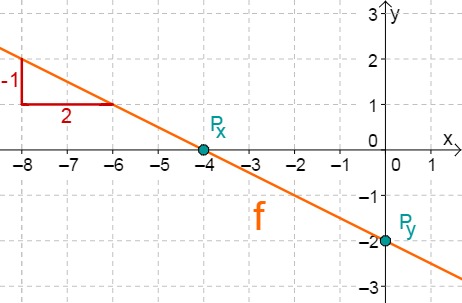
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
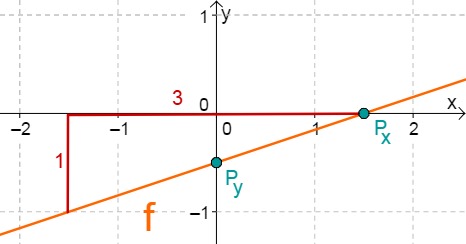
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
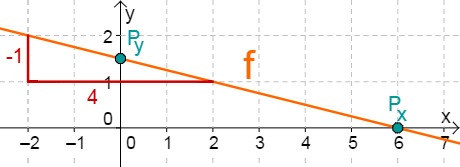
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
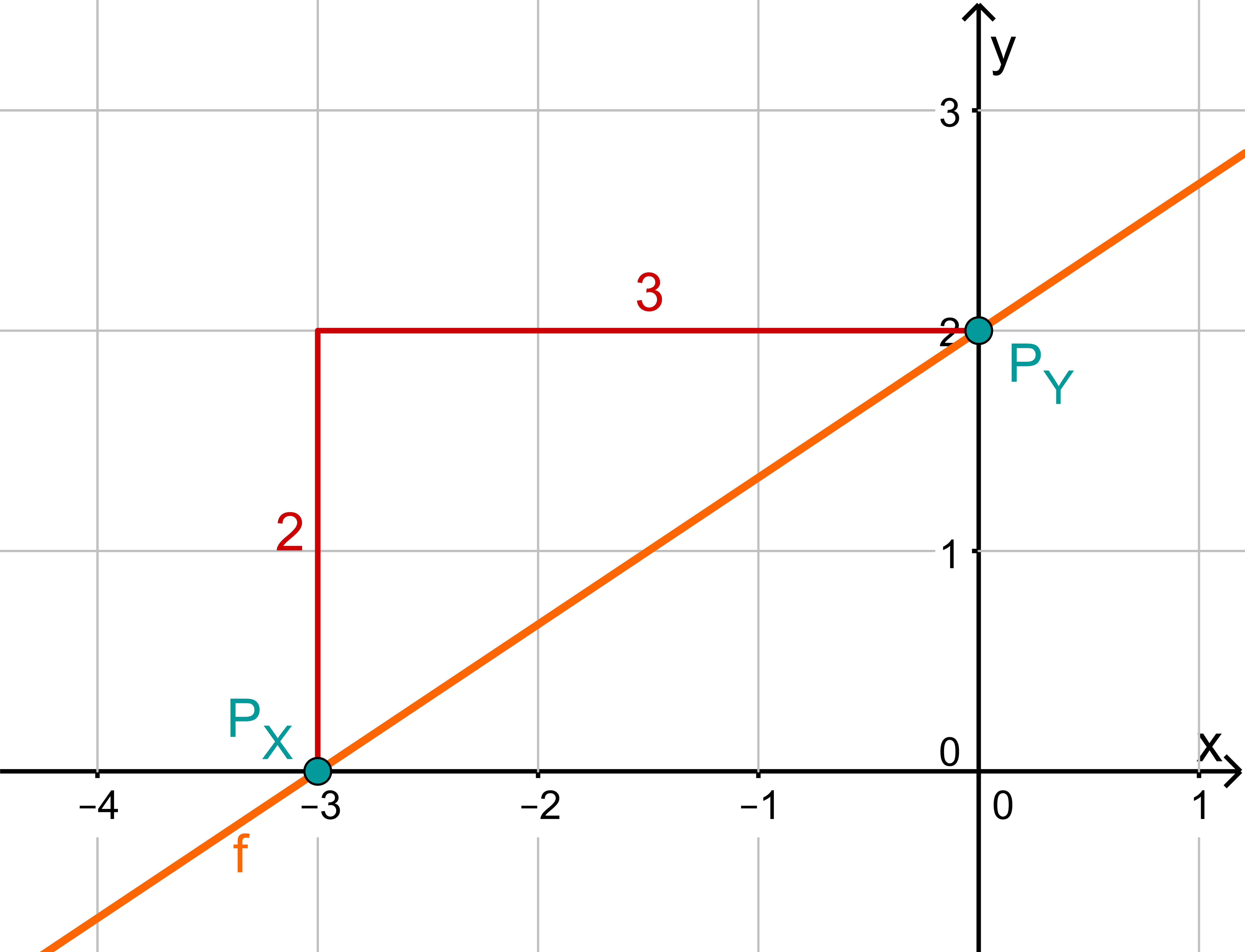
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
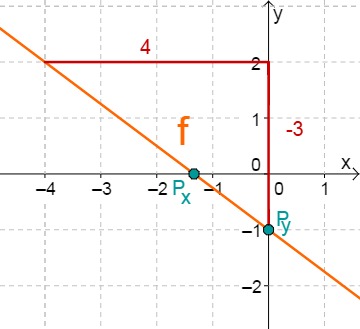
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
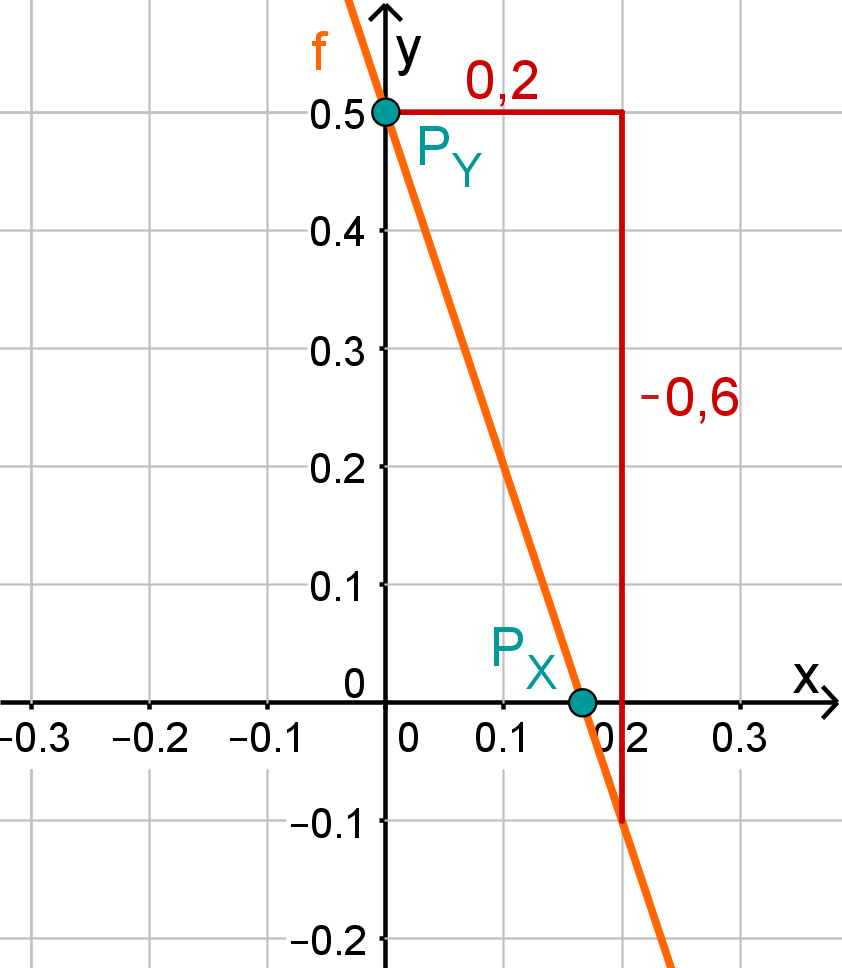
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
Hast du eine Frage oder Feedback?
- 5
Zeichne die Geraden und in ein Koordinatensystem. Bestimme die Nullstellen und den Schnittpunkt der Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Zeichne die Graphen
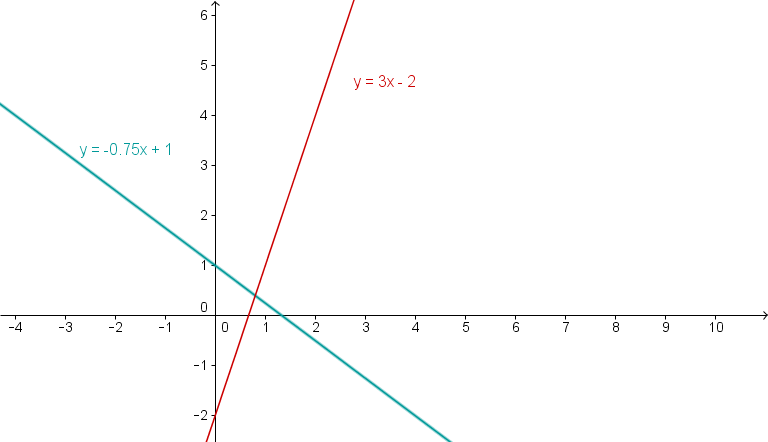
Bestimmung der Nullstellen
Setze y=0 um die Nullstelle zu bestimmen. Denn an der Stelle, an der y=0, schneidet die Gerade die x-Achse.
↓ Die erste Gerade hat bei eine Nullstelle.
Gehe für die zweite Gerade genauso vor.
↓ Setze y=0 um die Nullstelle zu bestimmen.
↓ Du dividierst durch einen Bruch Multipliziere mit dem Kehrwert
↓ Die zweite Gerade hat bei eine Nullstelle.
Bestimmung des Schnittpunkts
Setze die beiden Funktionsgleichungen gleich. Die Geraden schneiden sich dort, wo beide an der gleichen x-Stelle denselben y-Wert haben.
↓ Setze in eine der beiden Funktionen ein.
Der Schnittpunkt liegt bei .
- 6
Bestimme von folgenden Geraden die Schnittpunkte mit den Koordinatenachsen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Klammer auflösen
Um eine allgemeine Geradengleichung zu erhalten, multipliziere die Klammer aus.
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein und löse nach auf.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Gleichung umstellen
Um eine allgemeine Geradengleichung zu erhalten, vertausche auf der rechten Seite beide Elemente.
Schnittpunkt mit der x-Achse
Berechne den Schnittpunkt der Geraden mit der x-Achse.
Setze dazu den Ausdruck für die Geradengleichung gleich 0 und löse nach auf.
Die Gerade schneidet die x-Achse bei .
Schnittpunkt mit der y-Achse
Berechne den Schnittpunkt der Geraden mit der y-Achse.
Setze dazu in den Ausdruck für die Geradengleichung den Wert ein.
Die Gerade schneidet die y-Achse bei .
Hast du eine Frage oder Feedback?
- 7
Stelle die Funktionsgleichung für die Gerade durch die Punkte P(-25|30) und Q(55|-30) auf und berechne den Schnittpunkt der Gerade mit der x-Achse.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung ermitteln
P(-25|30); Q(55|-30)
Ermittle die Steigung m der allgemeinen Geradengleichung mithilfe des Differenzenqotienten .
Setze m und die Koordinaten eines Punktes z. B. P(-25|30) in die allgemeine Geradengleichung ein.
Vereinfache:
↓ Löse nach t auf.
↓ Setze m und t in die allgemeine Geradengleichung ein.
An der Schnittstelle mit der x-Achse ist der y-Wert 0.
Nach x auflösen. Stelle dafür das x alleine durch:
Beachte, dass bei beide Summanden multipliziert werden müssen.
Addiere 15
Die Gerade schneidet die x-Achse bei S(15|0).
- 8
Forme die Gleichung so um, dass sie die Form hat.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
↓ Der Bruch auf der rechten Seite fällt weg da .
↓ Linke und rechte Seite vertauschen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
↓ Beachte: Auf der rechten Seite der Gleichung wird jedes Element der Subtraktion mit multipliziert.
Die einzelnen Multiplikationen:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung umformen
↓ Die Klammer ausmultiplizieren.
Hast du eine Frage oder Feedback?
- 9
Zwei Geraden und schneiden sich auf der x-Achse in x=4.
Bestimmen Sie mögliche Funktionsterme.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Für diese Aufgabe gibt es keine eindeutige Lösung. Gesucht sind zwei verschiedenen lineare Funktionen, die beide durch den Punkt (4|0) laufen.
Ein sehr einfaches Beispiel wäre , also die x-Achse und . läuft offensichtlich durch (4|0). Für g(x) lässt sich das auch sehr einfach überprüfen: .
Andere mögliche Funktionen sind: , (allgemein für beliebige a)
Überlege durch welchen Punkt beide Geraden gehen müssen.
Bestimme zwei verschiedene Funktionen, die durch diesen Punkt gehen.
- 10
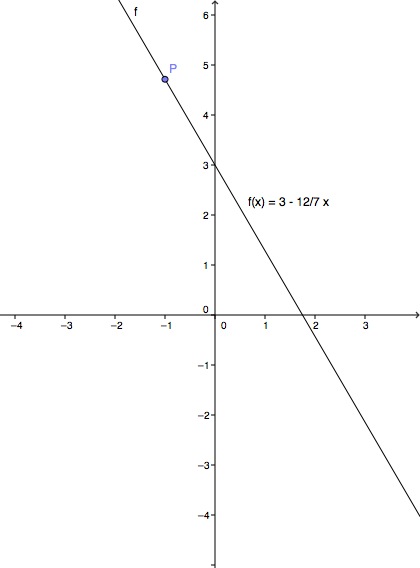
Gegeben ist die lineare Funktion .
Zeichne den Graphen und markiere den Funktionswert .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion zeichnen
Zeichne den Graphen der Funktion und kennzeichne .
Hast du eine Frage oder Feedback?
Liegt der Punkt auf dem Graphen von ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraph interpretieren
Prüfe, ob der Punkt auf dem Graphen der Funktion liegt.
Setze dazu den -Wert in die Funktionsgleichung ein.
↓ Multipliziere.
↓ Subtrahiere.
Ergebnis
Der Punkt liegt nicht auf dem Graphen, da der Funktionswert von ein nicht endender Dezimalbruch ist und nicht der endliche Dezimalbruch . Solltest du mit gerundeten Werten gerechnet haben, kannst du zum Schluss kommen, dass der Punkt im Graphen enthalten sei. Dies ist nicht der Fall.
Hast du eine Frage oder Feedback?
- 11
Gegeben sind die Geraden und .
Überprüfe, ob die Punkte , , , und auf einer der Geraden liegen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Überprüfung mit Skizze
Wähle jeweils einen beliebigen Punkt auf der Geraden, z. B. die y-Achsenabschnitte und . Gehe von dort nach rechts und entsprechen der Steigungen nach oben und nach unten. Verbinde jeweils die beiden Punkte zu einer Geraden.
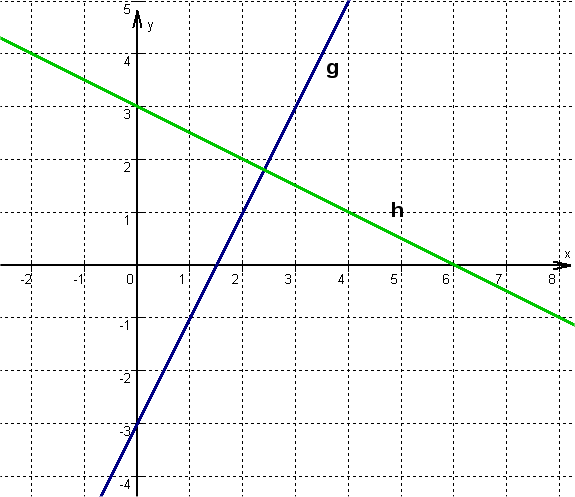
Wenn du den Verlauf der Geraden betrachtest und beispielsweise die Lage des Punktes , so siehst du, dass dieser kaum auf der Geraden h, wahrscheinlich aber auf liegen wird. Ähnlich kannst du bei anderen Punkten entscheiden, ob sich eine rechnerische Überprüfung lohnt: Punkt kann z. B. nur auf liegen.
Rechnerische Überprüfung
in einsetzen:
Setze die Koordinaten der Punkte in die fragliche Gleichung ein. Also setze und ein.
Das ist eine wahre Aussage.
⇒ liegt auf .
liegt auf keiner der Geraden. Das kann eindeutig der Skizze entnommen werden.
in einsetzen:
⇒
Diese Aussage ist falsch, also liegt nicht auf
in einsetzen:
⇒
Diese Aussage ist falsch, also liegt nicht auf .
in einsetzen:
Diese Aussage ist richtig, also liegt auf .
Hast du eine Frage oder Feedback?
Ergänze die Koordinaten so, dass die Punkte auf h liegen: P(5 | ?) , Q(-3,5 | ?) , R(? | 12) , S(? | -7,5).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Koordinaten ergänzen
; P(5|?)
Die gegebene Koordinate des Punktes (die x-Koordinate) wird in die Funktionsgleichung eingesetzt und daraus die fehlende y-Koordinate berechnet.
⇒ P(5|0,5)
Q: Q(-3,5|4,75)
R: R(-18|12)
S: S(2 1|-7,5).
Hast du eine Frage oder Feedback?
Zeige, dass T(2,4|1,8) auf beiden Geraden liegt. Was bedeutet dies?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Beweis für T
T(2,4|1,8)
Die Koordinaten von T in beide Geradengleichungen einsetzen. Wenn die Aussagen wahr sind, liegt T auf den Geraden.
in g:
in h:
Beide Gleichungen ergeben richtige Aussagen, also liegt der Punkt T auf beiden Geraden.
T Ist der Schnittpunkt der Geraden
Hast du eine Frage oder Feedback?
- 12
Wo ist der y-Achsenabschnitt? Klicke drauf!
- 13
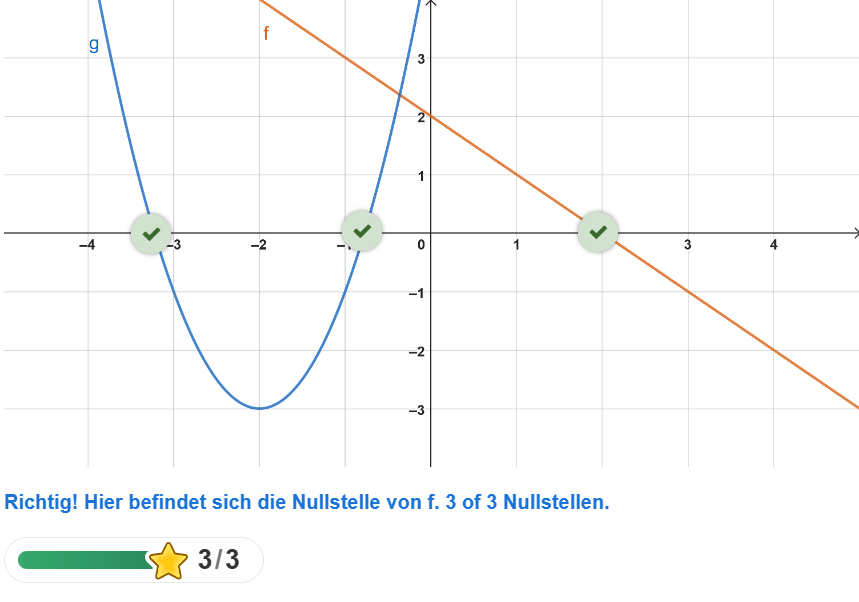
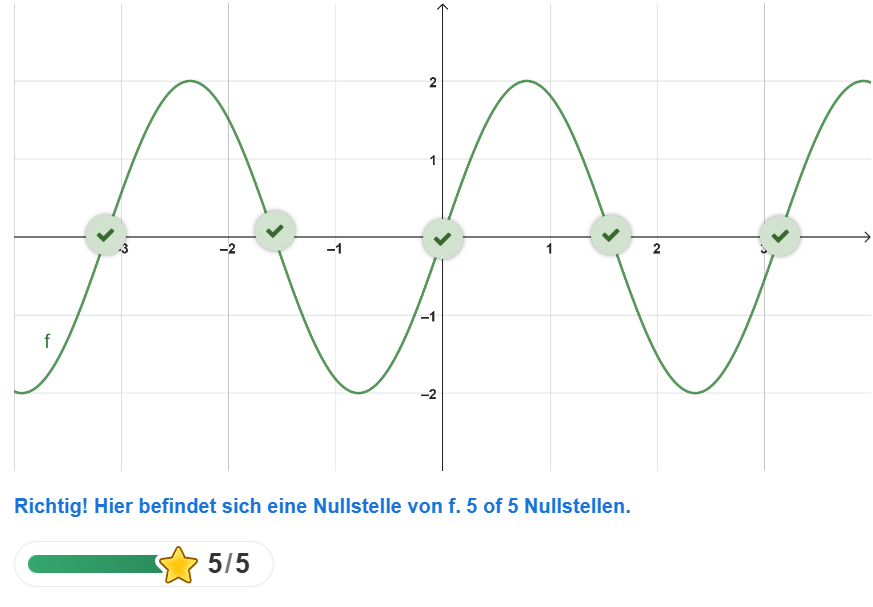
Hier geht es um: Nullstellen im Koordinatensystem erkennen!
Um die Nullstellen einer Funktion zu berechnen, muss man die x-Werte finden, für die f(x)=0 ist, das heißt, die Stellen, an denen sich die Funktion mit der x-Achse schneidet.
Wähle die Stellen aus, an denen sich die Funktion f mit der x-Achse schneidet!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?