Analysis, Teil A, Aufgabengruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Gegeben ist die Funktion mit maximalem Definitionsbereich .
Bestimmen Sie und geben Sie die Koordinaten des Schnittpunkts des Graphen von mit der y-Achse an. (3 P)
Geben Sie einen Term der ersten Ableitungsfunktion von an. (2 P)
- 2
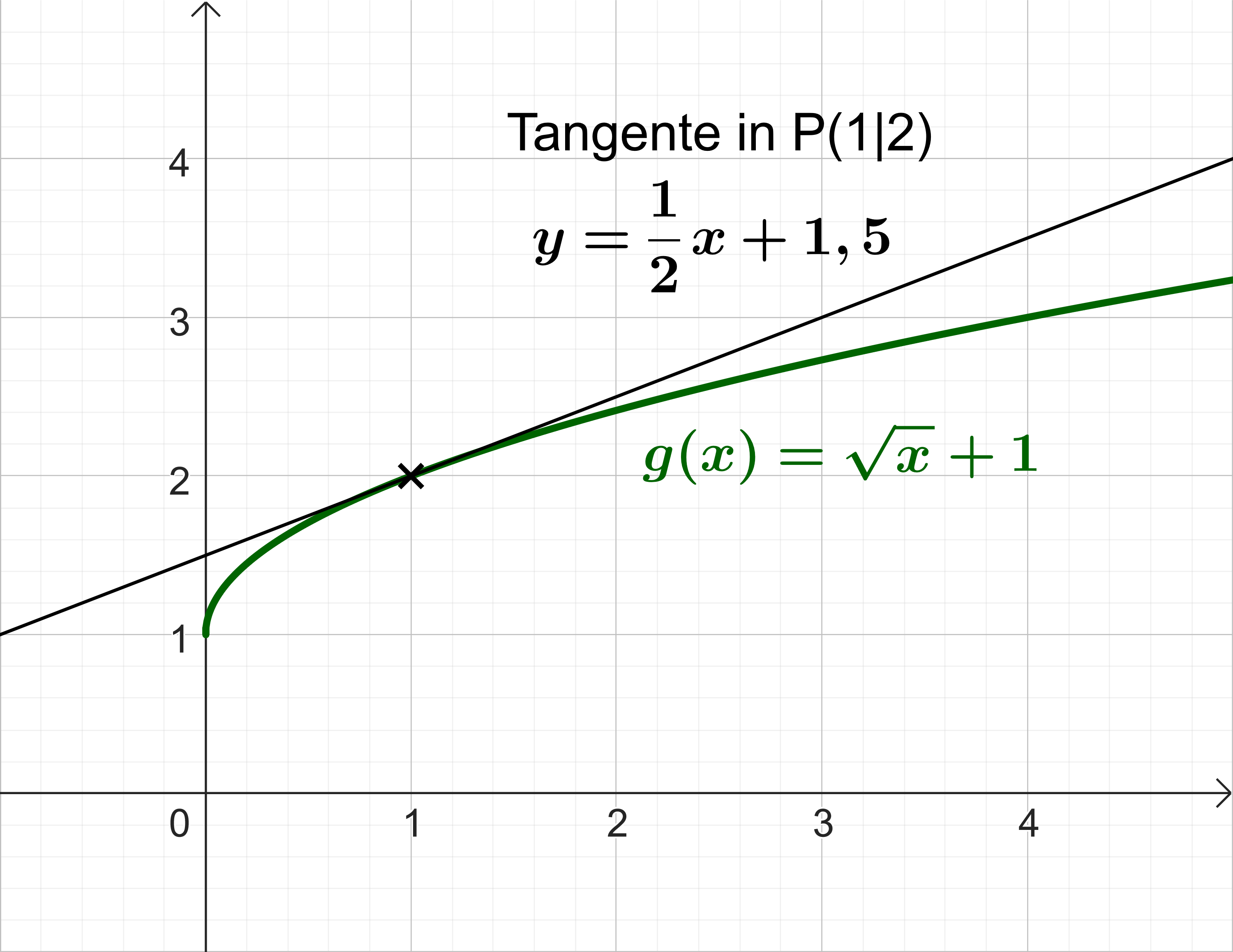
Gegeben ist die in definierte Funktion
Bestimmen Sie eine Gleichung der Tangente an den Graphen von im Punkt (3 P)
Die Funktion ist umkehrbar. Die Umkehrfunktion von g ist in [ definiert. Bestimmen Sie einen Term von (2 P)
- 3
Gegeben ist die in definierte Funktion mit
Die Nullstellen von sind und .
Zeigen Sie, dass das Flächenstück, das der Graph von mit der x-Achse einschließt, den Inhalt hat. (2 P)
Der Hochpunkt des Graphen von liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vergleiche Abbildung 1). Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von mit der x-Achse einschließt, überein. Bestimmen Sie den Wert von . (3 P)
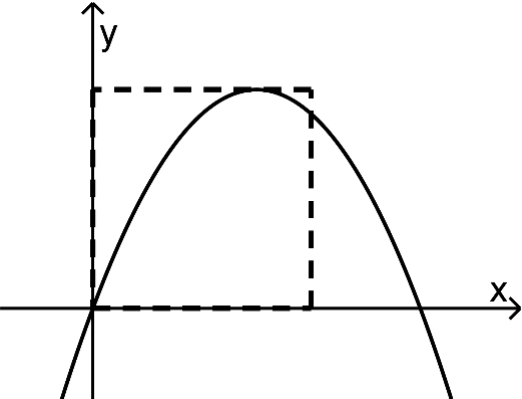
Abb.1
- 4
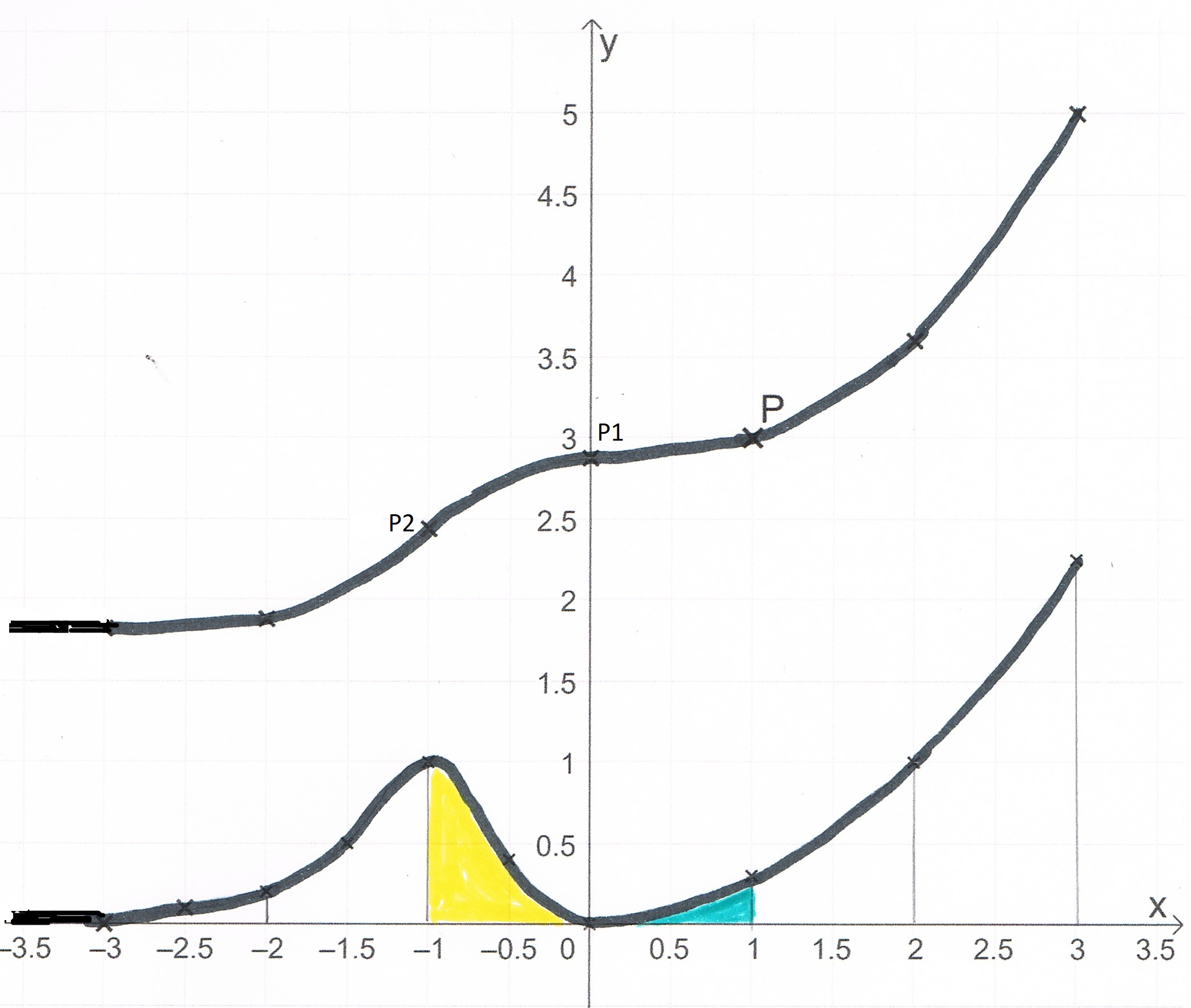
Abbildung 2 zeigt den Graphen der in definierten Funktion , dessen einzige Extrempunkte und sind, sowie den Punkt .
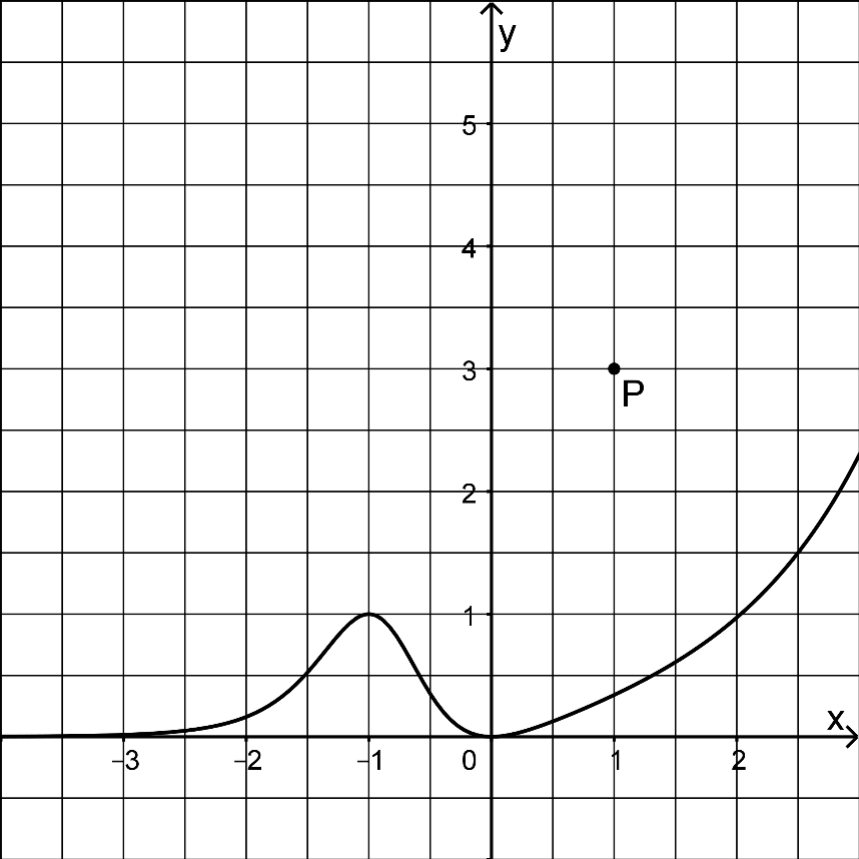
Abb. 2
Geben Sie die Koordinaten des Tiefpunkts des Graphen, der in
definierten Funktion mit an. (2 P)
Der Graph einer Stammfunktion von verläuft durch . Skizzieren Sie diesen Graphen in Abbildung 2. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?